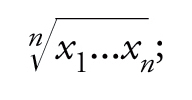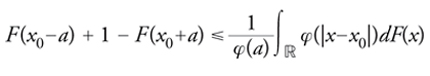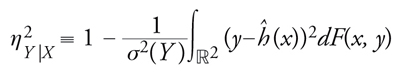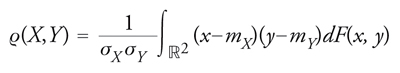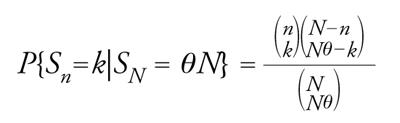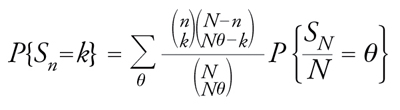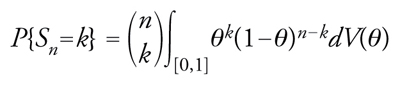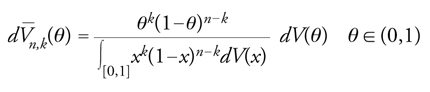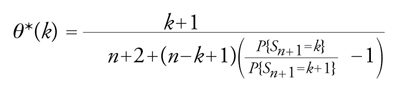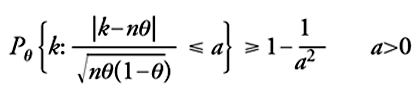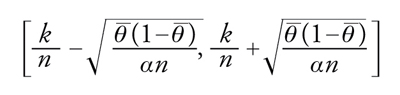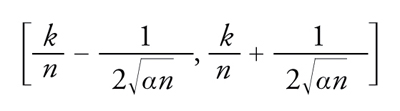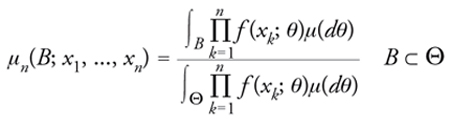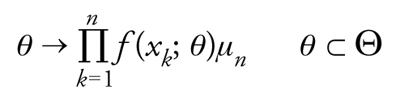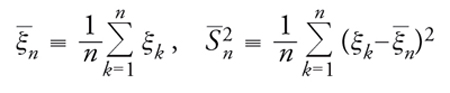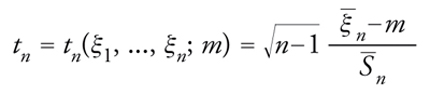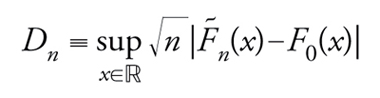Statistica

Statistica

La maggior parte delle indagini e degli esperimenti ‒ siano essi condotti a scopi di natura scientifica oppure per esigenze di tipo industriale, realizzati su larga scala oppure in piccolo ‒ producono dati che devono essere analizzati. Lo scopo dei metodi statistici consiste in sostanza nell'estrarre informazioni utili da essi. In questo articolo intendiamo trattare principalmente quei metodi statistici che considerano i dati come realizzazioni di fenomeni aleatori, cui è associata una specifica legge di probabilità. Spesso si designa il complesso di questi metodi col termine di statistica matematica. Oggi, la diffusione dei metodi statistici è soprattutto collegata al ruolo fondamentale da essi giocato in relazione alla logica induttiva nel senso suggerito dal teorema di Bayes. Tuttavia, occorre parimenti segnalare che a partire dagli anni Ottanta del XX sec. si sono affermati punti di vista alternativi rispetto a quello bayesiano. Tra questi ultimi, la corrente di pensiero che ha avuto maggior successo è legata all'opera di Ronald A. Fischer e dei suoi seguaci.

Prima di considerare i metodi della statistica matematica presenteremo alcune nozioni basilari di statistica descrittiva, termine che è tradizionalmente usato per indicare il complesso dei metodi di descrizione di una distribuzione statistica in relazione agli scopi concreti di un'indagine specifica. Il compito principale della statistica descrittiva è quello di individuare le forme più significative in cui possono essere espresse rilevanti caratteristiche sintetiche di una distribuzione. Per presentare qualche aspetto notevole dei metodi descrittivi, cominciamo con il considerare N individui e supponiamo che una certa loro caratteristica assuma s distinte modalità C₁,C₂,...,C_s.

Suddividendo gli individui in base alla specifica modalità posseduta si ottengono s gruppi di numerosità rispettive N₁,N₂,...,N_s e deve naturalmente risultare N₁+...+N_s=N.I rapporti f_h≡N_h/N (h=1,...,s) si dicono frequenze e la funzione φ, definita sulla classe di tutti i sottoinsiemi di {C₁,...,C_s} in modo che per ogni A⊂{C₁,...,C_s} il suo valore φ(A) coincida con la somma delle frequenze associate agli elementi di A, è un esempio di distribuzione di frequenze o, come spesso si preferisce dire, di distribuzione statistica. Il lettore attento avrà senz'altro constatato che φ è formalmente una distribuzione di probabilità. Tuttavia, la differenza fra i due tipi di distribuzione è sul piano concettuale profonda. Infatti, se φ fosse una probabilità, φ(A) fornirebbe una valutazione della plausibilità dell'evento (generalmente aleatorio) A, mentre con φ frequenza, φ(A) informa semplicemente sulla maggiore o minore presenza di unità statistiche in A. Una distribuzione statistica ammette sempre un'interpretazione come distribuzione di probabilità: se si sceglie uno degli N individui in modo che ogni individuo abbia la stessa probabilità 1/N di essere estratto, allora la probabilità che la modalità presentata dall'individuo scelto appartenga ad A coincide con φ(A). Quello appena presentato è un esempio di distribuzione su uno spazio discreto con s punti.

Come le probabilità, anche le distribuzioni statistiche possono essere definite su spazi di infiniti elementi e spalmate su tali spazi con continuità, specialmente quando esse siano il risultato di operazioni di interpolazione, mediante opportuni modelli, di distribuzioni effettive, per loro natura quasi sempre discrete. Se una distribuzione è definita sull'asse reale ℝ, un modo per descriverla è fare ricorso alla funzione di ripartizione; quest'ultima è definita in modo tale che a ogni punto x di ℝ fa corrispondere la massa (frequenza o probabilità) concentrata sulla semiretta (−∞,x]. Se esiste una funzione f (non negativa) tale che la funzione di ripartizione in ogni punto x si possa esprimere mediante l'integrale ∫x_−∞ f (u)du, allora f si dice funzione di densità e può essere usata per descrivere la distribuzione.

Spesso non è necessario conoscere in ogni dettaglio la distribuzione delle masse. In meccanica, per esempio, spesso basta determinare il baricentro e la massa totale di un corpo, mentre il modo in cui tale massa è distribuita non ha alcuna importanza ai fini della risoluzione del problema preso in considerazione. Analogamente, nel contesto degli studi economici per determinare il reddito totale di una collettività di redditieri non è necessario conoscere la distribuzione del reddito; sono sufficienti i dati relativi al reddito medio e al numero dei redditieri.

Medie e indici di variabilità

Tra i concetti più significativi mediante i quali si possono esprimere rilevanti caratteristiche sintetiche di una distribuzione, ci limiteremo a considerare quelli di media e indice di variabilità.

Per media di due o più numeri x₁,...,x_n s'intende spesso (seguendo Cauchy) un valore compreso fra il minimo e il massimo di essi, espresso di solito mediante semplici formule (media aritmetica: (x₁+...+x_n)/n; geometrica:

armonica: [(x₁⁻¹+...+x_n⁻¹)/n]⁻¹; quadratica: √(x₁²+...+x_n²)/n; esponenziale: log_a[(a^x1+...+a^xn )/n]; ecc.). Come in più occasioni ebbe a scrivere Bruno de Finetti, la nozione assurge a valore significativo nell'interpretazione datane nel 1929 da Oscar Chisini: media di più grandezze è un valore comune che si potrebbe attribuire a tutte senza alterare una certa circostanza che interessa. La media ha dunque un carattere relativo: a certi effetti serve bene una media, per altri ne occorrono di tipo diverso. Più formalmente, la media di x₁,x₂,...,x_n rispetto a una circostanza esprimibile mediante la funzione V è un valore di x per cui

[1] V(x₁, x₂, ..., x_n) = V(x, x, ..., x).

La definizione data da Chisini si può estendere, come fece de Finetti nel 1931, al caso più espressivo di una generica distribuzione: media di una distribuzione caratterizzata dalla funzione di ripartizione F rispetto a una circostanza esprimibile mediante una funzione V* (definita su una classe di funzioni di ripartizione contenente le degeneri, che assegnano la frequenza, o massa, unitaria su un punto a e indicheremo con D_a un valore di x per cui

[2] V*(F ) = V*(D_x).

Le medie che scaturiscono dalla definizione originaria di Chisini rientrano nella seconda, quando F è discreta con un numero finito di valori x₁,...,x_n distinti, cui è associata la stessa frequenza 1/n.

Una media M è detta monotona se M(F₁)>M(F₂) quando le funzioni di ripartizione F_i con i=1,2 sono tali che F₁(x)≤F₂(x) per ogni x e F₁(x₀)〈F₂(x₀) per qualche x₀; è associativa se, date F₁,F₂,...,F_m tali che F=λ₁F₁+...+λ_mF_m con λ_i≥0 (i=1,...,m) e λ₁+...+λ_m=1, si ha M(F)=λ₁M(F₁)+...+λ_mM(F_m). Le medie più importanti sono monotone e associative.

Per un bel teorema dimostrato indipendentemente da Mitio Nagumo e Andreij N. Kolmogorov nel 1930 e esteso a distribuzioni da de Finetti nel 1931, la media M(·), definita sulla classe delle funzioni di ripartizione che distribuiscono la massa unitaria in un assegnato intervallo chiuso e limitato [a,b], è monotona e associativa se e solo se esiste una funzione φ continua e strettamente monotona tale che, per ogni funzione di ripartizione F della classe suddetta, si ha

[3] M(F) = φ⁻¹(∫_[a,b] φ(x)dF(x)).

Così si ottengono: la media aritmetica con φ(x)=x; la media geometrica con φ(x)=logx; la media armonica con φ(x)=1/x; la media quadratica con φ(x)=x², ecc.

Sebbene il concetto di media dovuto a Chisini sia il più significativo quando applicabile, si possono presentare circostanze in cui la definizione deve essere basata su altri criteri. Tra di essi merita di essere ricordato quello consistente nel minimizzare uno scarto medio. In meccanica è noto che il baricentro è il punto rispetto al quale è minimo il momento di inerzia; in effetti è facile dimostrare che il valore di m₁ che rende minimo l'errore quadratico medio m→(∫_ℝ |x−m|²dF(x)) deve coincidere con la media aritmetica ∫_ℝ xdF(x); invece, quello che rende minimo l'errore medio assoluto m→(∫_ℝ |x−m|dF(x)) deve coincidere con una mediana di F, ovvero un qualunque valore m₀ che 'divide a metà' la distribuzione: F(m₀)≥1/2 e, simultaneamente, F(m₀)≤1/2.

Gli scarti medi di una distribuzione F, attorno a un fissato x₀, definiti da

[4] S_φ(F, x₀) = φ⁻¹(∫_ℝ φ(|x−x₀|)dF(x))

mediante una funzione φ con le stesse proprietà di quella che interviene nell'espressione delle medie associative, sono considerati misure della variabilità di F e più precisamente della dispersione o addensamento della distribuzione attorno a x₀. Lo scarto quadratico medio (equivalentemente, la varianza) è il più noto indice di dispersione. Una celebre disuguaglianza di Markov dà una giustificazione effettiva della precedente affermazione, ponendo in relazione gli scarti con la massa concentrata nelle code della distribuzione: per a>0 e φ continua e strettamente crescente, vale

[5] formula

Pertanto, se l'indice di dispersione che compare a destra ha un valore relativamente piccolo rispetto a φ(a), deve essere necessariamente grande la probabilità concentrata attorno ad x₀ in quanto sarà piccola quella concentrata nelle code.

Una distribuzione può essere analizzata anche sotto il profilo della mutua variabilità dei suoi valori (non si fa intervenire alcun punto di riferimento x₀). Ricorrendo al linguaggio della probabilità, s'immagini di effettuare due osservazioni a caso, indipendenti e identicamente distribuite secondo la funzione di ripartizione F, di una grandezza la cui distribuzione di frequenza è F. Allora, il numero

[6] φ⁻¹(∫_ℝ2 φ(|x−y|)dF(x)dF(y))

dà un'indicazione del valor medio della diversità di dette osservazioni e quindi della mutua variabilità fra gli elementi del dominio di F. Celebre è la differenza media, che si ottiene dalla precedente con φ(x)=x.

Distribuzioni statistiche e relazioni statistiche

L'idea posta alla base dei criteri consistenti nella minimizzazione di un errore medio si presta bene a essere usata per l'analisi delle relazioni statistiche di due o più attributi di un gruppo di individui. Limitatamente al caso bidimensionale, supponiamo di suddividere N individui in base alle modalità di due caratteri congiuntamente posseduti.

Indicando con C₁,...,C_s le modalità del primo e con D₁,...,D_r quelle del secondo, si ottengono s×r grup-pi G₁₁,...,G_1r,...,G_s1,...,G_sr di numerosità N₁₁,...,N_sr (N₁₁+...+N_sr=N). Il rapporto N_ij/N rappresenta la frequenza con cui la i-esima modalità del primo carattere si combina alla j-esima modalità del secondo. Allora, se entrambi hanno per realizzazioni dei numeri reali, la loro funzione di ripartizione (congiunta) F è definita in modo che, per ogni coppia ordinata (x,y) di numeri reali, F(x,y) rappresenta la frequenza con cui un valore non superiore a x del primo carattere si combina con uno non superiore a y del secondo. Perciò, F₁(x)=lim_y→∞F(x,y) e F₂(y)=lim_y→∞F(x,y) forniscono rispettivamente la funzione di ripartizione del primo e del secondo carattere calcolate in x e in y.

Con riferimento a questa situazione, spesso si presenta il problema di estrarre da F informazioni circa l'eventuale tendenza di una caratteristica a dipendere funzionalmente dall'altra. La questione, spesso presentata come ricerca di una relazione statistica fra esse, può essere vista da un'angolazione più propriamente probabilistica come problema di previsione: data la coppia (X,Y) di numeri aleatori con funzione di ripartizione F, come usare il fatto che si conosca la determinazione di X per stimare quella di Y? Ovviamente, la stima riuscirà tanto più precisa quanto più alto sarà l'addensamento della massa (probabilità, in questo caso specifico) attorno al grafico di una qualche funzione di Y su X. Un primo passo verso la soluzione del problema posto è quello di cercare una funzione ĥ tale che Ŷ≡ĥ (X) sia il più vicino possibile a Y, secondo un fissato criterio di vicinanza. Adottando ancora una volta il criterio della minimizzazione dell'errore quadratico medio, si cercherà ĥ in modo che

[7] ∫_ℝ2(y−ĥ (x))²dF(x, y) = min_h ∫_ℝ2(y−h(x))²dF(x, y)

dove h varia nell'insieme delle funzioni reali per cui sia finito l'integrale scritto a destra. In virtù di un importante teorema (che taluno indica come principio della regressione), si trova

[8] ĥ (x)∫_ℝ ydF_2|1(y|x) x ∈ ℝ

essendo F_2|1 la distribuzione condizionata di Y sotto l'ipotesi che X prenda il valore x. La funzione ĥ (·), coincidente col valore atteso di detta distribuzione condizionata, è nota come funzione di regressione di Y su X.

Nel 1905, Karl Pearson propose una misura sintetica dell'intensità della dipendenza di Y da X, nota come rapporto di correlazione:

[9] formula

esso varia nell'intervallo [0,1], assumendo il valore massimo 1 se e solo se la distribuzione del vettore aleatorio (X,Y) è concentrata sul grafico Y=ĥ (X) come è naturale attendersi in caso di perfetta dipendenza di Y da X. D'altro canto, il valore minimo 0 è raggiunto quando ĥ (·) è costante e quindi uguale al valore atteso di Y, una situazione detta di indipendenza regressiva rispetto al problema della previsione di Y: la conoscenza di X non apporta informazioni utili.

Talvolta, la ricerca del minimo di [7] viene ristretta alle funzioni h dalla forma h(x)=ax+b; il risultato è detto retta di regressione (o retta dei minimi quadrati) e la sua espressione è data da

[10] formula

dove ϱ è il classico coefficiente di correlazione lineare

[11] formula

e σ_X, σ_Y indicano gli scarti quadrici medi di X e Y.

Tale coefficiente misura l'intensità della dipendenza lineare di Y da X: esso varia infatti in [−1,1] e assume i valori 1 o −1 se e solo se la distribuzione di (X,Y) è concentrata su una retta rispettivamente crescente o decrescente.

Induzione statistica. Il punto di vista bayesiano

Classicamente, l'induzione statistica si distingue per i seguenti aspetti: (a) l'evento E di cui si parla consta di diversi fatti E₁,E₂,...; (b) questi fatti sono analoghi (per es., perché relativi a prove successive eseguite in condizioni analoghe).

Limitandoci per semplicità al caso di una successione di eventi, un modello probabilistico idoneo per sviluppare il ragionamento induttivo è quello delle successioni scambiabili, proposto a tale scopo da de Finetti tra il 1928 e il 1931. In effetti, un modo coerente per tradurre in termini probabilistici la seconda delle condizioni sopra richiamate è quello di ritenere che per ogni n la probabilità di ogni realizzazione di (E₁,...,E_n) dipenda soltanto dal numero dei successi e da n mentre, a parità di questi elementi, non varia al variare dell'ordine con cui successi e insuccessi si susseguono. Se la legge di (E₁,E₂,...) gode di questa proprietà d'invarianza rispetto a permutazioni finite, allora gli eventi E₁,E₂,... si dicono scambiabili. Si noti che soddisfano questa condizione gli elementi delle successioni bernoulliane, le cui leggi sono determinanti nella rappresentazione della più generale legge scambiabile. Quest'aspetto merita particolare attenzione in rapporto alla specificità dell'induzione statistica. In primo luogo la frequenza di successo S_n/n, calcolata per (E₁,...,E_n) con E₁,E₂,... scambiabili, converge in legge e cioè esiste una funzione monotona non decrescente V (con V(x)=0 per ogni x〈0 e V(x)=1 per ogni x≥1) tale che la probabilità che S_n/n non superi x converge per n→+∞ a V(x) in ogni punto x di continuità per V. D'altro canto, sotto la condizione di scambiabilità grazie a un semplice ragionamento combinatorio si trova che, se (ⁿ_k)≡n!/k!(n−k)!, vale la relazione

[12] formula

con n,N interi positivi che soddisfano 0〈n〈N, k intero positivo compreso fra max{0,n−N(1−θ)} e min{n,N} e θ un elemento di {0,1/n,2/n,...,(N−1)/N,1}. Allora

[13] formula

da cui, passando al limite per N→+∞, si trova

[14] formula

per ogni k in {0,1,...,n}. Ne segue immediatamente che una qualunque combinazione di successi e insuccessi (secondo un ordine assegnato) sulle prime n prove ha probabilità

[15] ∫_[0,1]θ^k(1−θ)^n−kdV(θ)

dove k è il numero dei successi. La [15], che esprime il teorema di rappresentazione di de Finetti per successioni infinite di eventi scambiabili, significa che per determinare tale legge basta assegnare la distribuzione limite, rappresentata da V, della frequenza di successo al divergere del numero delle prove. Dalla [15] si ottiene la soluzione del problema elementare della statistica (in condizioni di scambiabilità), consistente nella ricerca della probabilità p_k⁽ⁿ⁾ di avere successo in una futura prova condizionatamente all'ipotesi di avere osservato k successi nelle prime n:

[16] formula

dove ovviamente

[17] formula

V__n,k (·) è nota in statistica come distribuzione finale (subordinata a un risultato sperimentale) in contrapposizione alla distribuzione iniziale V. La [17] costituisce una significativa estensione del teorema di Bayes: essa descrive come si trasforma la distribuzione di probabilità (iniziale) della frequenza limite in seguito all'osservazione (ipotetica) di un (qualunque) risultato sulle prime n prove. La determinazione e l'uso di V__n,k sono di primario interesse nei problemi in cui essa corrisponde, insieme a V, alla legge di un elemento aleatorio θ∼ effettivamente osservabile come per esempio la frazione incognita dei possessori di una specifica modalità di un carattere dicotomico in una popolazione statistica.

A proposito dell'uso di V__n,k, oltre alla determinazio-ne di p_k⁽ⁿ⁾ si può citare il problema della stima di θ∼. La situazione più significativa si presenta quando sia specificata una funzione di danno esprimente la penalizzazione da applicare in corrispondenza dell'errore |θ∼−θ_n*| dovuto all'attribuzione del valore θ_n* alla grandezza incognita θ∼, dove la stima θ_n* dipende dal risultato di un numero n generico di prove. Tipicamente, la penalizzazione l sarà espressa da una funzione strettamente crescente sull'insieme dei reali non negativi e uguale a zero in zero come l(x)=x o l(x)=x². Si dice allora stimatore bayesiano di θ∼ una qualunque funzione θ_n*=θ_n*(k) in corrispondenza della quale risulta minimo il cosiddetto rischio bayesiano

[18] R(l; k; n) = ∫_[0,1]l (|θ−θ*_n(k)|)dV__n,k(θ).

Per esempio, nel caso l(|θ−θ_n*(k)|)=|θ−θ_n*(k)| il rischio è minimo quando per stima di θ∼ si prende una media di V__n,k. Ancora, prendendo l(|θ−θ_n*(k)|)=|θ−θ_n*(k)|² si trova che la stima bayesiana di θ∼ deve coincidere col valore atteso di V__n,k.

La distribuzione finale V__n,k può anche essere usata per determinare stime per intervalli di θ∼, consistenti appunto nell'individuazione di intervalli, preferibilmente di piccola lunghezza, nei quali θ∼ cada con probabilità non inferiore a un certo livello (1−α). Il caso più significativo si ha quando si riesca a determinare a_n(k) e b_n(k), con a_n(k)〈b_n(k), in modo che

[19] b_n(k) − a_n(k) =

= min{b−a tale che V__n,k(b)−V__n,k(a) ≥ 1−α}.

In una simile circostanza, (a_n(k),b_n(k)] si potrà interpretare come intervallo di stima per θ∼ di livello 1−α.

L'introduzione di funzioni di danno e rischio nella risoluzione di problemi statistici avviene sistematicamente a partire dagli anni immediatamente successivi al secondo conflitto mondiale: secondo un punto di vista non bayesiano, per opera di Abrahm Wald e coerentemente con la concezione bayesiana grazie a Leonard J. Savage. Eppure nel 1738, con ben due secoli d'anticipo, Daniel Bernoulli aveva individuato i primi elementi di una teoria delle decisioni in condizioni d'incertezza spiegando l'importanza del ruolo che vi poteva giocare la nozione di speranza morale. Un'anticipazione evidente, questa, della moderna teoria dell'utilità e quindi della teoria delle decisioni statistiche.

Induzione statistica. Alternative al punto di vista bayesiano

L'impiego indiscriminato del metodo della distribuzione finale per la risoluzione di pseudoproblemi relativi a entità metafisiche assimilate a elementi aleatori gettò tale discredito sul teorema di Bayes quale strumento per l'induzione statistica che, a partire dal secondo decennio del secolo scorso, si imposero punti di vista chiaramente alternativi a quello bayesiano. La corrente di pensiero che in tale direzione fece più seguaci è legata al nome di Ronald A. Fisher. Per dare una sintesi delle idee di questo studioso eminente, si può partire dall'espressione (^N−n_Nθ∼−k)/(^N_Nθ∼): si tratta, nell'impostazione bayesiana, della probabilità di avere una certa sequenza di successi e insuccessi in n prove, subordinata all'ipotesi che la frequenza di successo in una successione più lunga di N>n prove sia pari a θ∼. Fisher ne rifiuta l'interpretazione come probabilità di evento subordinato poiché θ∼ ha una determinazione ben precisa, ancorché incognita, che va sottratta a giudizi soggettivi di probabilità. I metodi statistici hanno allora il compito di indicare modi di argomentare logicamente accettabili ai fini dell'approssimazione della vera determinazione di θ∼. Quando N è abbastanza grande rispetto a n come spesso capita nei casi concreti, l'espressione precedente si può sostituire con la probabilità bernoulliana θ∼^k(1−θ∼)^n−k.

Escluso quindi l'intervento di distribuzioni iniziali, i metodi statistici devono basarsi esclusivamente sulle espressioni ricordate. Di esse Fisher enfatizza una interpretazione quali indicatori del grado di verosimiglianza dei valori ammissibili di θ∼, visto come parametro incognito. In effetti, se si fissa che in n estrazioni si siano verificati k successi, la funzione

[20] θ → θ^k (1−θ)^n−k θ ∈ (0,1)

segnala che in corrispondenza dei valori di θ per cui assume i valori più elevati del codominio risulta relativamente più elevata la probabilità di osservare (in n prove) k successi. Fisher non esita a ritenere che la determinazione più verosimile del parametro incognito si debba cercare fra tali valori; procede quindi a definire lo stimatore di massima verosimiglianza come il punto θ∼_n(k) in corrispondenza del quale la funzione di verosimiglianza [20] raggiunge il valore massimo del codominio. Evidentemente θ∼_n(k) coincide con la frequenza di successo k/n, mentre lo stimatore bayesiano di θ∼ coincidente col valore atteso di V__n,k sarebbe uguale a

[21] formula.

L'interesse di quest'ultima espressione risiede nella dipendenza, che essa rende esplicita, dello stimatore bayesiano dalla frequenza di successo nelle prove eseguite. In particolare per dV(θ)=dθ (postulato di Bayes) si avrebbe P{S_n=k}=1/(n+1), con k=0,1,...,n e n≥1, e quindi θ*_n(k)=(k+1)/(n+2). Nelle condizioni del postulato di Bayes, lo stimatore di massima verosimiglianza verrebbe a coincidere col valore modale della densità finale θ→dV__n,k(θ)/dθ=(n+1)!(x^k(1−θ)^n−k)/(k!(n−k)!).

Per quanto concerne la costruzione di stime per intervalli, nell'impostazione propugnata da Fisher una certa cautela va posta in relazione alla corretta interpretazione a causa del fatto che θ∼ non è da considerarsi come variabile aleatoria. Infatti, grazie alla disuguaglianza di Bienaymé-Čebyšëv si ha

[22] formula

dove P_θ è la legge di probabilità della successione bernoulliana quando il parametro θ∼ prenda il valore θ. Pertanto, fissato a in (0,1), basta scegliere a=1/√__α per rica-vare: P_θ {|k−nθ|/√nθ(1−θ)≤1/√α}≥1−α. Da questa sideduce che, qualunque sia il valore θ_ del parametro incognito, la probabilità corrispondente che l'intervallo aleatorio

[23] formula

contenga θ non è inferiore a 1−α. L'aleatorietà dell'intervallo dipende dal fatto che aleatoria è la frequenza k/n di successo nelle prime n prove. Ovviamente, l'intervallo precedente non ha valore pratico perché nella sua espressione figura il parametro incognito, ma l'inconveniente può essere facilmente eliminato considerandone uno più ampio sulla base del fatto che vale max_θ∈[0,1]θ(1−θ)=1/4. Perciò,

[24] formula

è un intervallo che risponde all'esigenza di stimare il parametro incognito sulla base del risultato osservato in n prove. Si noti dunque che non è lecito affermare che il parametro cade in [24] con probabilità maggiore o uguale a 1−α, in quanto il parametro non è visto come elemento aleatorio dotato di legge di probabilità. Al contrario, nell'impostazione di Fisher è corretto dire che qualunque sia il valore vero del parametro incognito l'intervallo [24], caratterizzato dall'avere estremi dipendenti dall'esito aleatorio dell'esperimento, ha probabilità maggiore o uguale a 1−α di contenere il vero valore.

Estensioni

Le considerazioni svolte a proposito delle successioni bernoulliane si estendono agli altri modelli statistici. L'estensione non presenta novità rilevanti dal punto di vista concettuale, ma coinvolge un apparato tecnico-formale più specifico.

Abbiamo accennato all'estensione del concetto di scambiabilità a successioni di osservazioni a valori in un generico spazio X. Nei casi concreti, X corrisponderà quasi sempre a uno spazio metrico particolare e la classe degli eventi coinciderà con la σ-algebra di Borel X su tale spazio (la più piccola fra le σ-algebre di parti di X che contengono tutti gli aperti di X). Indicati con ξ₁,ξ₂,... gli elementi aleatori associati ai possibili risultati delle singole osservazioni, diciamo che essi costituiscono una successione scambiabile quando la legge di probabilità di (ξ₁,...,ξ_n) è, per ogni n, uguale a quella di (ξ_π(1),...,ξ_π(n)) per ogni permutazione π degli indici 1,...,n. Quindi, lo schema della scambiabilità ben si attaglia alle situazioni sperimentali di prove successive eseguite in condizioni analoghe. Il teorema di de Finetti (l'espressione [15] nel caso di prove bernoulliane) si estende alla situazione più generale nei termini seguenti. Se la legge di probabili-tà di una successione aleatoria (ξ_n)_n≥1 a valori in (X,X) soddisfa

[25] P{ξ₁∈A₁, ..., ξ_n∈A_n_} = ∫_{Θ k=1}∏ⁿ l(A_k; θ)μ(dθ)

per ogni A_k in X(k=1,...,n) e per ogni n, con μ e l(·;θ) (per ogni θ) misure di probabilità rispettivamente su (X,X) e su un'opportuna σ-algebra di parti di un insieme Θ, allora (ξ_n)_n≥1 è scambiabile; viceversa, se (ξ_n)_n≥1 è scambiabile, la sua legge soddisfa [25] per una scelta opportuna di {l(·;θ): θ∈Θ}e μ.

In accordo con un'altra e forse più comune formulazione del precedente teorema, la successione (ξ_n)_n≥1 risulta essere scambiabile se e solo se la sua legge di probabilità è una mistura di leggi di processi binomiali, dove per processo binomiale si intende una successione di elementi aleatori a valori indipendenti e identicamente distribuiti in (X,X). Nell'espressione [25] si hanno leggi di processi binomiali per ogni θ ‒ determinate dai prodotti ∏ⁿ_k=1l(A_k;θ) ‒ e di esse si prende il baricentro (mistura) determinato dalla legge μ. In statistica, l'elemento aleatorio θ∼ dotato di legge (di cui θ in Θ è una generica realizzazione) si dice parametro incognito e costituisce l'oggetto di inferenza statistica bayesiana, laddove le ipotesi concernenti le sue determinazioni abbiano un significato oggettivo nel senso che corrispondono a fatti. Strumento essenziale per l'inferenza statistica su θ∼ è la sua distribuzione finale μ_n(·;x₁,...,x_n), ovvero la legge condizionale di θ∼ dato il risultato {ξ₁=x₁,...,ξ_n=x_n} per le prime n osservazioni. Sotto opportune condizioni tecniche, la più rilevante delle quali è l'esistenza per ogni θ di una funzione di densità f (·;θ) di l(·;θ) (ovvero, tale che l(A;θ)==∫_A f (x;θ)ϱ(dx) per ogni A in X), la distribuzione finale si può calcolare per mezzo della seguente estensione del teorema di Bayes

[26] formula

la quale include come caso particolarissimo la formula [17]. Dalla distribuzione finale si passa alla distribuzione predittiva p_n(·;x₁,...,x_n): si tratta della legge di probabilità condizionale di una qualunque osservazione, a partire dalla (n+1)-esima in poi, dato il risultato {ξ₁=x₁,...,ξ_n=x_n} sulle prime n:

[27] p_n(A; x₁, ..., x_n_) = ∫_Θ l(A; θ)μ_n_(dθ; x₁, ..., x_n_) A ⊂ X.

La critica di Fisher ai metodi bayesiani, basata sull'impiego delle distribuzioni finale e predittiva, riguarda il coinvolgimento della legge iniziale μ in quanto veicolo di elementi soggettivi nell'inferenza statistica. Quindi, così come nel caso più semplice degli eventi propone di fondare i metodi statistici sulla [20], anche nel caso più generale egli indica la funzione di verosimiglianza

[28] formula

come fondamento dell'induzione statistica. Per esempio, i problemi di stima (sia puntuale che per regioni di confidenza) andranno affrontati dallo stesso punto di vista descritto a proposito degli esperimenti a due valori, fatte salve eventuali ulteriori difficoltà tecniche legate alla scelta di specifiche espressioni per f (·;θ) in relazione ai campi specifici d'indagine.

Criteri di significatività

Si tratta di procedure ideate per controllare alla luce di dati sperimentali l'attendibilità di ipotesi statistiche, intendendo con quest'ultimo termine una qualunque congettura sul paramentro incognito caratterizzante un dato modello statistico. Solitamente la natura delle ipotesi in questione porta a specificare un valore particolare del parametro, o un sottoinsieme di Θ, cui corrisponde una situazione di peculiare interesse. Per esempio, si immagini di volere confrontare l'efficacia di due farmaci indicati per la cura dell'insonnia sulla base dei risultati osservati su un certo gruppo di n pazienti. Si indichino rispettivamente con τ₁ e τ₂ i tempi di sonno guadagnati da un singolo paziente grazie rispettivamente a una dose del primo e del secondo farmaco. La differenza ξ=τ₁−τ₂ dà una misura della diversità della loro efficacia sul singolo paziente. Quindi, si avranno n numeri aleatori ξ₁,...,ξ_n associati agli n pazienti del gruppo. Nell'ipotesi che sussistano le condizioni per ritenere tali elementi aleatori indipendenti e identicamente distribuiti con legge gaussiana di media m e varianza σ², una supposizione di notevole interesse è quella che asserisce nullo il valore di m: essa esprime la congettura che i due farmaci abbiano sostanzialmente lo stesso effetto. Il problema fondamentale cui la statistica dovrebbe dare una risposta è quello di decidere se i dati sperimentali relativi agli n pazienti smentiscano o non smentiscano l'ipotesi H₀≡{m=0}.

Allora, una volta formulato il problema di verifica di ipotesi, si deve cercare una partizione dello spazio dei risultati possibili delle osservazioni (spazio dei campioni) in due classi: quella di rifiuto e quella di non rifiuto di H₀. Se i valori osservati cadono nella prima classe l'ipotesi si ritiene smentita mentre, se i valori osservati appartengono alla seconda, essa non è scartata almeno fino a quando una successiva raccolta di dati non ne decreti il rifiuto. La determinazione della partizione, o meglio dei criteri suggeriti per individuarla, è da effettuarsi prima dell'acquisizione dei dati e dipende dalla risposta che s'intende dare alla domanda: quando possiamo ritenere che delle informazioni smentiscano un'ipotesi statistica? Da decenni sulla base di una metodologia statistica da molti condivisa, i ricercatori rispondono con la proposta di significance tests, ossia di criteri di significatività.

Tali criteri si estrinsecano in procedure così congegnate: viene fissato un livello di significatività α (un numero positivo, generalmente vicino a zero) e si ricerca una regione dello spazio dei campioni tale che la probabilità per (ξ₁,...,ξ_n) di appartenervi non superi α quando H₀ è vera. Ovviamente, il fatto che le n osservazioni effettuate cadano proprio nella regione di rifiuto non può essere considerato una dimostrazione della falsità logica di H₀. D'altro canto, supponiamo che in un'ipotetica sequenza di repliche dello stesso esperimento (consistente, a sua volta, in n osservazioni) si sia verificato un evento che secondo un'interpretazione empirico-asintotica della probabilità ha bassissima possibilità di presentarsi quando l'ipotesi H₀ è vera: secondo i sostenitori dei significance test sarebbe allora auspicabile rigettarla.

Una parte notevole della letteratura statistica è stata e viene tuttora dedicata alla ricerca di forme ottimali di criteri di significatività, seguendo l'indirizzo fissato originariamente da Fisher e (partendo da una concezione diversa) da Jerzy Neyman e Egon S. Pearson. Uno dei criteri più celebri, utile per esempio al fine di rispondere al concreto problema poc'anzi descritto della misura dell'efficacia dei due farmaci, è il test di Student; proposto da William S. Gosset, deve il suo nome allo pseudonimo da lui usato nel lavoro del 1908 in cui lo presentò. Si pone

[29] formula

e si dice t di Student la formula

[30] formula

dove S__n è la radice quadrata aritmetica di S__n². Gosset trovò che la legge di probabilità di t è indipendente da m e σ². La sua densità, proporzionale a {1+t²/(n−1)}^−n/2 con t∈ℝ, va sotto il nome di legge della t di Student con n−1 gradi di libertà. Si può quindi determinare t_α>0 in modo che risulti uguale ad α la probabilità dell'evento {|t|≥t_α}. Per esempio, per α=0,01 e n=10 si ha t_α=3,250. Determinato t_α, si pone m=0 (il valore corrispondente all'ipotesi H₀) e si fissa la regione di rifiuto in modo da farla coincidere con l'insieme delle n-uple ordinate (x₁,...,x_n) in corrispondenza delle quali |t_n(x₁,...,x_n;0)| supera t_α.Quindi, se nell'esempio concreto si ha n=10, α=0,01 e si osservano valori (differenze dei tempi di sonno guadagnati dai dieci pazienti) di ξ₁,...,ξ_n per cui ξ__n=1,58, S__n=1,167 e quindi t₀=4,06, la procedura ideata da Gosset suggerisce di rifiutare H₀ o di non rifiutare l'idea che il primo farmaco sia più efficace del secondo.

Altro esempio giustamente celebre di criterio (non parametrico questa volta) riguarda la bontà dell'adattamento di un modello ai dati. Fissata una funzione di ripartizione F₀, si intende decidere se vada rifiutata l'ipotesi che la legge dei singoli elementi di un campione ‒ supposti indipendenti e identicamente distribuiti ‒ coincida con F₀. Indicata, per ogni x, la frazione degli elementi del campione non superiori a x col simbolo F∼_n(x) (la cosiddetta funzione di ripartizione empirica) Kolmogorov scoprì nel 1933 che la legge di probabilità di

[31] formula

non varia al variare di F₀ nella classe delle funzioni di ripartizione continue. Inoltre, al tendere a infinito del numero n di osservazioni, D_n ha una legge di probabilitàlimite coincidente con quella di sup_x∈ℝ|B*(x)|, dove B* denota il cosiddetto ponte browniano. Questo termine designa un processo di Wiener-Lévy {B(t):0≤t≤1} subordinato alla condizione {B(1)=0}. Allora, fissato α (se n è sufficientemente grande e K(·) indica la succitata funzione di ripartizione limite) l'ipotesi verrà rifiutata in corrispondenza dei campioni per cui D_n>c_α, con c_α determinato in modo che risulti K(c_α)=1−α.

bibliografia

De Finetti 1930: De Finetti, Bruno, Funzione caratteristica di un fenomeno aleatorio, "Atti della Reale Accademia Nazionale dei Lincei, Memorie", 4, 1930, pp. 86-133.

De Finetti 1931: De Finetti, Bruno, Sul concetto di media, "Giornale dell'Istituto Italiano degli Attuari", 2, pp. 369-396.

De Finetti 1937: De Finetti, Bruno, La prévision: ses lois logiques, ses sources subjectives, "Annales de l'Institut Henri Poincaré", 7, 1937, pp. 1-68.

De Finetti 1959: De Finetti, Bruno, La probabilità e la statistica nei rapporti con l'induzione, secondo i diversi punti di vista, in: Atti del corso CIME su induzione e statistica, Roma, Cremonese, 1959.

Fisher 1950: Fisher, Ronald A., Contributions to mathematical statistics, New York, Wiley, 1950.

Fisher 1971: Fisher, Ronald A., The collected papers of R.A. Fisher, edited by J.H. Bennett, Adelaide, University of Adelaide, 1971.

Kolmogorov 1933: Kolmogorov, Andrej N., Sulla determinazione empirica di una legge di distribuzione. "Giornale dell'Istituto Italiano degli Attuari", 4, 1933, pp. 92-99.

Kotz 2004: Encyclopedia of statistical sciences, edited by Samuel Kotz e altri, New York, Wiley, 2004.

Lehmann, Casella 1998: Lehmann, Erich L. - Casella, George, Theory of point estimation, 2. ed., New York, Springer, 1998.

Lehmann, Casella 2005: Lehmann, Erich L. - Romano, Joseph P., Testing statistical hypotheses, 3. ed., New York, Springer, 2005.

Neyman, Pearson 1966: Neyman, Jerzy - Pearson, Egon S., Joint statistical papers, Berkeley, University of California Press, 1966.

Savage 1954: Savage, Leonard J., The foundations of statistics, New York, Wiley, 1954 (2. ed., New York, Dover, 1979).

Wald 1950: Wald, Abraham, Statistical decision functions, New York, Wiley, 1950.