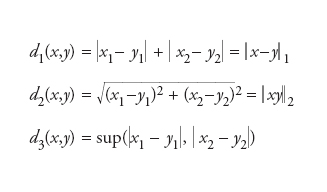spazio metrico
spazio metrico
Nozione introdotta nel 1906 da Maurice Fréchet e sviluppata poco dopo da Felix Hausdorff; è un risultato diretto dell’analisi delle principali proprietà astratte della distanza usuale. Per questa ragione essa deve essere considerata frutto del generale movimento di algebrizzazione della matematica avviatosi a partire dal XIX secolo. D’altro canto, l’estensione agli spazi metrici delle proprietà dello spazio euclideo definibili a partire dalla sola distanza introduce un linguaggio geometrico in numerosi problemi di algebra, analisi, teoria dei numeri. Si definisce quindi metrica su un insieme I un’applicazione d di I×I nell’insieme ℝ+ dei numeri reali positivi o nulli tale che: (a) d(x,y)=0 se e solo se x=y; (b) d(x,y)=d(y,x); (c) d(x,z)≤d(x,y)+d(y,z) per ogni x,y,z in I. La condizione (c) è detta disuguaglianza triangolare poiché non è altro che la generalizzazione della classica relazione tra le lunghezze dei lati di un triangolo. Un insieme I munito di una metrica si chiama spazio metrico. Se (I,d) e (I′,d′) sono due spazi metrici, una biezione f di I su I′ che conservi la distanza (cioè d′(f(x),f(y))=d(x,y) per ogni x,y in I) è detta isometria. Due spazi metrici sono detti isometrici se tra loro esiste un’isometria: le loro proprietà metriche saranno allora identiche. Se (I,d) è uno spazio metrico, allora ogni sottoinsieme S di I è uno spazio metrico, detto sottospazio di I, per la distanza d′ indotta da d attraverso la formula d′(x,y)=d(x,y) per x,y in S. Ogni insieme può essere munito della metrica detta banale, definita da d(x,y)=0, d(x,y)=1 se x≠y. Una classe importantissima di spazi metrici è costituita dagli spazi vettoriali normati, dove la distanza tra due elementi x,y è definita come norma della loro differenza: d(x,y)=∥x−y∥. La distanza così ottenuta è invariante per traslazioni, ovvero d(x+a,y+a)=d(x,y) per qualunque a,x,y. Per es., nel caso dello spazio ℝ2 (la generalizzazione a ℝn è immediata) è possibile definire a partire delle corrispondenti norme le distanze
dove x=(x1,x2), y=(y1,y2). Queste distanze verificano inoltre le disuguaglianze d3≤d2≤d1≤2d3. Una successione {xn}, n∈ℕ, si dice di Cauchy (o fondamentale) se per ogni ε>0 esiste un n0∈ℕ tale che d(xn,xm)〈ε per ogni m,n>0. Uno spazio metrico I si dice completo se ogni successione di Cauchy è convergente, ovvero il suo limite esiste ed è un elemento di I. In uno spazio metrico (I,d) si chiama palla aperta di centro x0 e raggio r>0 l’insieme dei punti la cui distanza da x0 è strettamente minore di r:B(x0,r)={x∈I tali che d(x,x0)〈r}. In maniera analoga si definisce la palla chiusa: B_ (x0,r)={x in I tali che d(x,x0)≤r}. Sottolineiamo che nonostante il nome una ‘palla’ non ha necessariamente forma sferica. Tornando alle distinte metriche definite sopra per ℝ2, notiamo che esse si traducono nelle inclusioni B3(x,r/2)⊂B2(x,r)⊂B3(x,r). A partire dalle palle è possibile definire su uno spazio metrico le fondamentali nozioni topologiche alla base dei metodi moderni dell’analisi matematica, anzi il concetto generale di topologia trae proprio da qui le sue origini. A questo fine, sarà infatti sufficiente definire aperto qualunque sottoinsieme S di uno spazio metrico (I,d) tale che per ogni x in S esiste r>0 sufficientemente piccolo affiché B(x,r)⊂S. Non è difficile poi convincersi che qualunque insieme aperto può essere costruito prendendo unioni (di un numero anche infinito) e intersezioni (di un numero finito) di palle aperte di I. È questa in realtà la definizione generale della struttura topologica che ogni metrica induce nello spazio sul quale è definita. Una definizione equivalente è possibile in termini di successioni convergenti. Siano ora (I,d) e (I′,d′) due spazi metrici e f una applicazione di I in I′. Si dice che f è continua in un punto x0 di I se per ogni numero reale ε>0 esiste un η>0 tale che se d(x0,x)〈η allora d′(f(x0),f(x))〈ε. In altre parole deve essere verificata l’inclusione B(x0,η)⊂f1(B′(f(x0),ε)) ovvero, ricordando la precedente definizione di aperto, f è continua in x0 se e soltanto se nell’immagine inversa per f di ogni aperto contenente f(x0) è possibile trovare un aperto contenente x0.