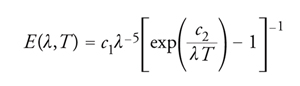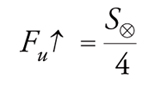Terra. Bilancio termico

Terra. Bilancio termico

Le osservazioni della temperatura media dell'atmosfera terrestre, registrate nell'ultimo secolo con sempre maggiore accuratezza, mostrano che il valore medio globale di questo parametro è aumentato di circa 0,8 °C negli ultimi 130 anni e, in particolare, di almeno 0,5 °C negli ultimi quarant'anni. Rispetto al periodo di riferimento di trent'anni che va dal 1951 al 1980, le anomalie di temperatura più rilevanti osservate tra il 2001 e il 2005 sono state individuate nella parte centrale della Siberia e nelle regioni dell'Oceano Artico più prossime al Polo Nord, con aumenti della temperatura media atmosferica compresi tra +1,6 e +2,2 °C, mentre anomalie comprese nell'intervallo +(1,2÷1,6) °C sono state individuate nell'Africa centrale, in vaste regioni dell'Asia orientale, in Nord America, nell'area amazzonica del Sud America e nella Penisola Antartica.

Questo processo di graduale riscaldamento della bassa atmosfera, osservato a tutte le latitudini, è attribuito principalmente all'aumento della concentrazione dei gas-serra e soprattutto a quello della concentrazione di anidride carbonica (CO₂), che ha raggiunto attualmente il valore medio di 380 ppmv, ovvero ben 100 ppmv al di sopra di quello di 280 ppmv riferito al periodo preindustriale (anno 1880). Si stima che i principali gas-serra (CO₂, CH₄, N₂O, clorofluorocarburi (CFC)) e gli altri gas in traccia abbiano prodotto una forzatura radiativa complessiva sul sistema climatico di +2,7 Wm⁻² dal 1880 al 2003, con un'incertezza stimata intorno al 15%. A questa forzatura se ne deve aggiungere un'altra dovuta all'ozono e al vapore acqueo stratosferico (che sta aumentando a causa dell'ossidazione del metano) e valutabile in +0,3 Wm⁻² dal 1880 a oggi. In contrapposizione a queste forzature radiative che inducono effetti di riscaldamento globale, vanno considerate quelle di segno negativo indotte direttamente dagli aerosol attraverso la riflessione e l'assorbimento della radiazione solare incidente e quelle prodotte dagli aerosol per via indiretta, attraverso le modifiche delle caratteristiche della copertura nuvolosa globale e delle proprietà riflettenti delle nubi. Si valuta che la forzatura radiativa diretta degli aerosol sia aumentata dal 1880 al 2005 fino a raggiungere un valore medio globale di −1,4 Wm⁻², mentre quella legata agli effetti indiretti ha raggiunto il valore di circa −1 Wm⁻² (l'incertezza di queste stime essendo del 50%). Gli aerosol stratosferici di origine vulcanica possono causare sporadici e limitati effetti di raffreddamento, non maggiori di qualche decimo di grado centigrado e per periodi di qualche anno. Si valuta che le attività antropiche legate all'agricoltura e alla deforestazione abbiano prodotto effetti minimi sul bilancio termico del nostro pianeta. Le variazioni naturali dell'irradianza solare entrante (ovvero della cosiddetta costante solare) hanno causato una forzatura di non più di 0,2 Wm⁻² dal 1880 al 2003, che appare essere assai modesta se confrontata con quella complessivamente associata all'effetto serra. Dunque, la variazione netta della forzatura radiativa effettiva dal 1880 al 2005 risulta essere di circa +1,8 Wm⁻², sostanzialmente definita come la differenza tra gli effetti di riscaldamento dovuti ai gas-serra e gli effetti di raffreddamento indotti dagli aerosol per via diretta e indiretta.

L'evoluzione del riscaldamento globale planetario è strettamente legata agli andamenti temporali delle forzature radiative, che agiscono sulla scala globale e su quelle regionali dalle variazioni di concentrazione dei gas-serra, degli aerosol e delle nubi, tali forzature essendo capaci di determinare situazioni di squilibrio e successivo riequilibrio su valori crescenti della temperatura atmosferica.

Per comprendere meglio come i vari effetti radiativi possano concorrere a causare il riscaldamento globale in atto, è opportuno esaminare i diversi processi radiativi che definiscono il bilancio termico della Terra: a tal fine, è utile tenere conto delle caratteristiche termodinamiche e di composizione dell'atmosfera e della struttura del sistema climatico terrestre e stimare in quale misura le varie forzature radiative interagiscono tra loro, contribuendo ad alterare il bilancio di energia del pianeta. Tali concetti sono presentati illustrando schematicamente i termini del bilancio termico terrestre e descrivendo i processi di scambio radiativo e di calore che hanno luogo nel sistema superficie-atmosfera, dovuti ai più importanti costituenti atmosferici (vapore acqueo, gas-serra, aerosol e nubi).

Il sistema Terra

Il pianeta Terra costituisce un sistema fisico termodinamicamente chiuso rispetto allo spazio esterno, dato che esso scambia energia con lo spazio solo in forma di radiazione. Allora, il bilancio di energia del sistema Terra-atmosfera è dato dalla somma di due termini radiativi: il primo (positivo) è indicato dal simbolo Φ_e, e definisce il flusso di radiazione che entra nel sistema nell'unità di tempo, il secondo (negativo) è indicato dal simbolo Φ_u, e definisce il flusso di radiazione uscente nel tempo unitario. La quantità Φ_e è data principalmente dalla radiazione solare (onda corta), che viene intercettata dalla Terra ed è in parte diffusa, assorbita o riflessa all'indietro dall'atmosfera e dalla superficie terrestre, mentre la quantità Φ_u è costituita dalla radiazione infrarossa (onda lunga), che viene emessa dal sistema superficie-atmosfera verso lo spazio.

Conseguentemente, i processi di trasferimento della radiazione solare e di quella infrarossa tra la superficie e l'atmosfera e tra la Terra e lo spazio dipendono: (a) dalle proprietà radiative della superficie del pianeta nel riflettere la radiazione solare e nell'emettere la radiazione termica; (b) dalle proprietà emissive della superficie; (c) dalle proprietà di emissione e assorbimento dei diversi strati atmosferici e, quindi, dalle caratteristiche termodinamiche e di composizione dell'atmosfera, rappresentate dai profili verticali di pressione, temperatura, umidità assoluta e concentrazioni dei vari costituenti atmosferici.

Le proprietà radiative della superficie terrestre

Il comportamento radiativo della superficie terrestre è descritto per mezzo di alcune grandezze fisiche: l'albedo, che definisce la capacità di una superficie nel riflettere la radiazione solare, l'emittanza cioè la capacità di una superficie nell'emettere radiazione infrarossa, e l'assorbanza, che definisce la capacità di una superficie nell'assorbire la radiazione infrarossa.

Albedo. - La superficie terrestre riflette la radiazione solare in percentuali diverse da un tipo di superficie all'altro, variabili in funzione della lunghezza d'onda e degli angoli di incidenza, riflessione e azimut della radiazione solare. Si definisce come albedo superficiale α_s la percentuale di radiazione solare riflessa da una superficie per un certo angolo di elevazione solare h, su tutto lo spettro da 0,3÷4 μm e su tutto il semispazio di riflessione. Il parametro α_s dipende principalmente dalle caratteristiche orografiche, dal tipo di copertura vegetale e dallo stato di umidità dei terreni, nel caso delle aree continentali, e nel caso delle aree oceaniche dall'intensità del moto ondoso provocato dal vento e dal contenuto clorofilliano del-le acque superficiali: (a) nelle superfici d'acqua, α_s assume valori più frequentemente compresi nell'intervallo 0,02÷0,05 per h>25° e valori crescenti al diminuire di h, fino a essere maggiori di 0,4 per h〈10°; (b) nelle terre umide continentali, α_s presenta valori compresi tra 0,05÷0,12 per h>25° e tra 0,12÷0,30 per h〈25°; (c) nelle terre coperte da vegetazione, α_s varia tra 0,10÷0,26, assumendo più spesso valori minori di 0,20 in presenza di foreste e maggiori di 0,20 in praterie e savane e subendo in entrambi i casi delle variazioni stagionali assai marcate; (d) nelle regioni desertiche, α_s può variare da 0,18 (in terreni sabbiosi grigiastri) a più di 0,50 (in aree desertiche ricche di cristalli di sale, come quelle degli alvei asciutti di laghi salati); (e) nelle regioni polari coperte da ghiacci marini e in quelle continentali innevate, α_s può presentare valori anche maggiori di 0,80 in presenza di neve fresca, compresi tra 0,70 e 0,80 in aree coperte da ghiacciai e più bassi, talvolta anche minori di 0,50, nei campi di neve di vecchia data.

A causa della variabilità stagionale delle aree continentali coperte da vegetazione o soggette a innevamento e della variabilità dell'angolo di incidenza della radiazione solare nel corso dell'anno, l'albedo superficiale media è soggetta a variare ampiamente da una regione all'altra del pianeta e da un mese all'altro. Considerando che circa il 65% della superficie terrestre è costituito dagli oceani e il restante 35% dalle terre emerse, si valuta che α_s possa avere un valore medio globale annuo prossimo a 0,14, se si assume che le superfici oceaniche presentino un valore medio annuo α_s=0,08 e le aree continentali (incluse quelle polari) un valore medio α_s=0,25, presentando valori medi mensili da 0,10 a 0,20.

Emittanza. - Per emittanza effettiva (ε_s) di una superficie s'intende il rapporto tra la densità di flusso della radiazione termica emessa da una superficie a una certa temperatura e la densità di flusso che sarebbe emessa da un corpo nero che si trova alla stessa temperatura, secondo la legge di Planck. La stessa grandezza fisica riferita a uno strato di materiale di spessore unitario e, quindi, anche all'atmosfera o al sistema superficie-atmosfera è più appropriatamente chiamata emissività.

All'interno dell'intervallo spettrale infrarosso 8÷13 μm, entro il quale l'atmosfera terrestre presenta i valori più alti di trasparenza, si valuta che i valori medi di emittanza possano variare negli intervalli: 0,966÷0,972 in terreni privi di vegetazione e secchi e in aree urbane; 0,977÷0,982 in terreni spogli, ricchi di sostanze organiche; 0,986÷0,991 in superfici d'acqua e in acquitrini; 0,970÷0,976 in terreni aridi coperti da arbusti sparsi; 0,973÷0,991 in aree di savana senza alberi, con valori medi di 0,974 nei periodi di siccità e di 0,989 nella stagione umida; tra 0,975 e 0,991 nella savana con alberi, con valori medi di 0,977 nei periodi di siccità e di 0,99 nella stagione umida; da 0,968 a 0,99 nelle foreste di latifoglie, con valori medi di 0,970 nei periodi di senescenza e di 0,989 nella stagione di crescita; e da 0,986 a 0,991 nelle foreste di aghifoglie, con valori medi di 0,987 nei periodi di senescenza e di 0,990 nella stagione di crescita.

Tenendo conto che l'emittanza degli oceani sull'intero spettro infrarosso è in media eguale a 0,99 e che quella delle terre emerse varia per lo più tra 0,92 e 0,98, si ottiene un valore medio globale di ε_s eguale a 0,975: dunque, la superficie terrestre emette come un corpo grigio, avendo caratteristiche di emittanza assai prossime a quelle di un corpo nero ideale.

Assorbanza. - Il principio di Kirchhoff stabilisce che il rapporto monocromatico tra il coefficiente di emissione per unità di massa di un certo materiale e il corrispondente coefficiente di assorbimento non dipende dal tipo di materiale ma è una funzione universale della lunghezza d'onda e della temperatura del materiale. Per queste condizioni, si può assumere realisticamente che ogni tipo di superficie presenti valori di assorbanza nell'infrarosso numericamente eguali a quelli di emittanza, l'assorbanza essendo definita dal rapporto tra la densità di flusso della radiazione assorbita da una superficie e la densità di flusso della radiazione incidente. L'assorbanza A_s di una superficie per la radiazione a onda lunga varia in funzione delle caratteristiche del terreno tra 0,92 e 0,99, le misure in campo forniscono valori medi di 0,978 su campi di neve, 0,956 su distese di sabbia, 0,971 per foreste di conifere e 0,981 per superfici erbose, cosicché il valore medio globale di A_s può essere valutato tra 0,97 e 0,98. Quando è riferita a uno strato di materiale di spessore unitario e, quindi, anche all'atmosfera o al sistema superficie-atmosfera, questa grandezza fisica prende il nome più appropriato di assorbitività.

Le caratteristiche termodinamiche e la composizione dell'atmosfera

L'atmosfera terrestre avvolge il nostro pianeta come un involucro gassoso di spessore assai modesto, se raffrontato con il raggio medio della Terra R_T=6370 km. A causa delle forze gravitazionali, l'atmosfera esercita una pressione dall'alto verso il basso, che assume il valore standard di 1013,25 hPa al livello del mare. La pressione atmosferica e la densità dell'aria decrescono al crescere dell'altezza seguendo una legge di forma esponenziale, definita sulla base dell'equazione idrostatica, cosicché le concentrazioni di massa dei vari costituenti atmosferici risultano decrescere esponenzialmente all'aumentare dell'altezza, assumendo un valore pari a 1/e (≈37%) del suo valore al livello del mare alla quota definita dalla cosiddetta altezza di scala H, che dipende per ogni costituente atmosferico dal peso molecolare, dalla temperatura dell'aria, dalla costante universale dei gas e dall'accelerazione di gravità. Nel caso dell'aria secca, avente peso molecolare di 28,96, l'altezza di scala H è valutata essere di 8 km, mentre i principali costituenti atmosferici presentano valori di H eguali a 8,26 km nel caso dell'azoto (avente concentrazione media di volume pari al 78,08%), 7,23 km per l'ossigeno (20,95%), 5,79 km per l'argo (0,93%), 12,84 km per il vapore acqueo (0÷4%), 5,26 km per l'anidride carbonica (380 ppmv) e 14,42 km per il metano (1,7 ppmv).

Per un valore della pressione atmosferica al livello del mare di 10³ hPa e per il valore di R_T dato sopra, si trova che la massa totale M_a dell'atmosfera terrestre è di 5,14×10¹⁸ kg, essendo l'accelerazione gravitazionale al suolo di 9,8 ms⁻². La pressione dell'aria diminuisce da un valore standard di 1013×10³ hPa al livello del mare a un valore medio di 265 hPa alla quota di 10 km, di 0,80 hPa a 50 km, e di 3×10⁻⁴ hPa all'altezza di 100 km. Sulla base delle caratteristiche del profilo verticale della temperatura dell'aria, l'atmosfera terrestre viene suddivisa in diverse regioni.

Troposfera. - Si estende dalla superficie terrestre fino alla quota di tropopausa, caratterizzata da un ampio minimo della temperatura: la quota della tropopausa varia in funzione della latitudine, essendo posta tra gli 8 e i 10 km alle alte latitudini, tra gli 11 e i 13 km alle medie latitudini, e intorno ai 17 km all'equatore, mentre la temperatura presenta valori medi al livello del mare compresi tra 300 K (alle basse latitudini) e 260 K (alle alte latitudini) e diminuisce con l'altezza con un gradiente verticale medio di −6,5 K/km fino alla quota di tropopausa, tale quota presentando valori prossimi a 220 K alle alte latitudini, di circa 215 K alle medie latitudini e al di sotto dei 200 K all'equatore. La troposfera contiene circa l'80% della massa atmosferica totale M_a ed è la regione atmosferica nella quale hanno luogo i principali processi radiativi e termici che definiscono il bilancio termico della Terra.

Stratosfera. - È la seconda regione atmosferica, deve il suo nome al fatto che essa è caratterizzata da condizioni di grande stabilità, a differenza di quelle marcatamente turbolente della troposfera: essa si estende dalla quota di tropopausa a quella di stratopausa, sita intorno ai 50 km, e ospita lo strato chiamato ozonosfera, presente in massima parte tra le quote di 20 e 40 km. La temperatura dell'aria si mantiene quasi costante per alcuni chilometri e poi sale rapidamente con l'altezza fino a raggiungere valori intorno ai 270 K alla quota di stratopausa, tale aumento della temperatura dell'aria essendo principalmente dovuto all'assorbimento della radiazione solare ultravioletta nei processi fotochimici di dissociazione delle molecole di ossigeno e ozono e alla liberazione di calore nelle reazioni chimiche secondarie che portano alla formazione dell'ozonosfera. La stratosfera contiene quasi tutto il restante 20% di M_a, dato che si valuta che la massa atmosferica totale al di sopra dei 50 km ammonti soltanto allo 0,1 della massa totale atmosferica.

Mesosfera. - La terza regione atmosferica, si estende dalla quota di stratopausa fino a quella della mesopausa, sita intorno agli 80÷85 km. La temperatura diminuisce con l'altezza da valori di 270 K circa alla stratopausa fino a valori intorno ai 180 K alla mesopausa.

Termosfera. - Si estende al di sopra della mesopausa, in essa la temperatura si mantiene pressoché costante fino a 90 km di altezza e poi sale rapidamente con l'altezza, fino a raggiungere valori di 600 K intorno alla quota di 150 km, nei periodi di limitata attività solare, e a superare i 2000 K alle quote intorno ai 400 km, quando l'attività solare attraversa i periodi di massima intensità.

La radiazione solare

tab. 1

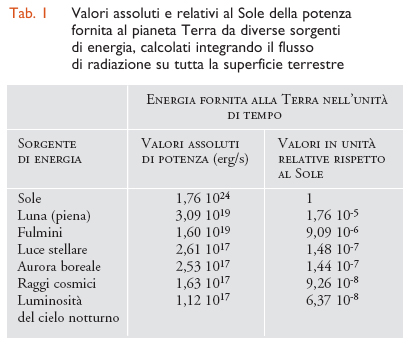
Il Sole fornisce il 99,997% dell'energia entrante nel sistema Terra-atmosfera, le altre sorgenti (come la Luna, la luce stellare e i raggi cosmici) contribuiscono in misura del tutto trascurabile (tab. 1). La quantità di radiazione solare incidente sul pianeta varia nel corso dell'anno in funzione della distanza Terra-Sole, mantenendosi entro il ±3,5% del suo valore medio annuo. Quest'ultimo valore prende il nome di costante solare S_⊗, definita come la quantità di radiazione solare che arriva nell'unità di tempo su un'area unitaria posta al di fuori dell'atmosfera terrestre, perpendicolarmente ai raggi solari, quando la distanza Terra-Sole è eguale al valore medio annuo, pari a 1 U.A. (1 unità astronomica è pari a 1,496×10⁸ km). La costante solare non si mantiene affatto stabile nel tempo ma è soggetta a variazioni cicliche legate alle fluttuazioni periodiche dell'attività solare, con periodi diversi di 11, 22, ∼44, 88, 130 e ∼200 anni. Pertanto, il valore di S_⊗ è oggetto di regolari e continue misurazioni: misure spettrali eseguite dalla NASA prima del 1971 hanno fornito un valore S_⊗=1353 Wm⁻². Misure radiometriche più recenti, eseguite regolarmente a partire dal 1969 presso il PMOD (Phisikalisch-Meteorologisches Observatorium di Davos) in Svizzera, stanno fornendo un valore di S_⊗=1367 W m⁻².

Lo spettro della radiazione solare

La curva spettrale di emissione di un corpo nero alla temperatura T è definita dalla legge di Planck, secondo cui la quantità di radiazione monocromatica emessa nell'unità di tempo dalla superficie unitaria di corpo nero è data da

[1] formula,

dove T è la temperatura di corpo nero misurata in K, λ è la lunghezza d'onda, c₁=3,7415×10⁻¹⁶ Wm⁻² e c₂=1,43879×10⁻² mK sono la prima e la seconda costante della radiazione, rispettivamente.

Integrando la [1] su tutto l'intervallo di lunghezza d'onda da 0 e ∞, si ottiene la legge di Stefan-Boltzmann:

[2] ∫₀^∞E(λ,T)dλ = εσT⁴

dove σ=5,6697×10⁻⁸ Wm⁻²K⁻⁴ è la costante di Stefan-Boltzmann e l'emittanza ε è assunta eguale a 1 in un corpo nero ideale.

Se si indica con R_T il raggio medio della Terra, comprendente anche il sottile spessore dell'atmosfera, il flusso totale medio Φ_e della radiazione solare intercettata dalla Terra è dato dal prodotto della costante solare S_⊗ per la sezione d'urto geometrica del pianeta, che è approssimativamente eguale a πR_T², essendo la Terra di forma quasi sferica. D'altra parte, il flusso Φ_u dovuto all'emissione di radiazione termica da parte di tutta la superficie terrestre va calcolato sulla superficie terrestre totale, approssimativamente eguale a 4πR_T². Allora, affinché siano soddisfatte le condizioni di equilibrio del bilancio di radiazione tra flusso entrante Φ_e e flusso uscente Φ_u, la densità di flusso uscente F_u↑ dovrà essere tale da soddisfare l'equazione

[3] Φ_e = πR_T² S_⊗ = 4πR_T² F_u↑ ,

ovvero

[4] formula.

Questa equazione stabilisce che si deve considerare solo un quarto di S_⊗ per definire il flusso entrante di radiazione solare, quando tale termine è confrontato con la densità di flusso uscente F_u↑, al fine di valutare i termini del bilancio di radiazione della Terra. Pertanto, la densità di flusso della radiazione solare in arrivo sulla superficie esterna del sistema Terra-atmosfera che va considerata nel bilancio termico è Q*=S_⊗/4=341,75 Wm⁻², arrotondato solitamente a 342 Wm⁻². Applicando la teoria di corpo nero al Sole e assumendo che l'integrale della [2] sia eguale al valore della costante solare S_⊗ misurato recentemente, si ottiene che la temperatura effettiva di corpo nero del Sole è T_⊗=5777 K. Ma considerando la legge dello spostamento di Wien,

[5] λ_maxT_w = 2,8978×10³ μm K,

fig. 2

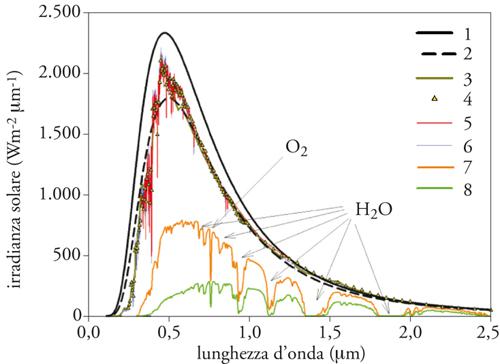
che stabilisce una relazione teorica tra la lunghezza d'onda λ_max di massima emissione di un corpo nero e temperatura apparente del Sole T_w, si ottiene T_w=6088 K, essendo λ_max=0,476 μm. Le curve di distribuzione spettrale dell'irradianza solare extraterrestre ottenute dalla [1] per la temperatura equivalente di corpo nero T_⊗=5777 K e per T_w=6088 K sono confrontate in fig. 2 con le curve spettrali misurate in diversi esperimenti e con le curve di irradianza solare diretta in arrivo al livello del mare, dopo il passaggio attraverso un'atmosfera standard per due diversi valori di h. La fig. 2 mostra anche che lo spettro della radiazione solare extraterrestre occupa per la massima parte l'intervallo di lunghezza d'onda λ 0,3÷4 μm, presentando: (a) una parte alquanto modesta, pari all'8,03%, nell'ultravioletto (λ〈0,40 μm); (b) una parte rilevante, pari al 44,69%, nel visibile (0,40≤λ≤0,76 μm); (c) una parte considerevole, pari al 47,28%, nell'infrarosso (0,76〈λ≤4 μm). La fig. 2 mostra anche che esiste un sostanziale accordo tra i dati sperimentali d'irradianza solare extraterrestre, ottenuti con diverse risoluzioni spettrali e che i dati sperimentali sono compresi tra le due curve teoriche di corpo nero corrispondenti alle temperature di 5777 e 6088 K. In particolare, i dati sperimentali nell'ultravioletto si accordano con temperature T_⊗ minori di 5700 K, quelli nel visibile con T_⊗ comprese tra 5900 e 6000 K, quelli del vicino infrarosso (λ〈1 μm) con T_⊗≈5800 K e quelli aventi λ>1 μm con T_⊗≈6100 K. Queste differenze spettrali si spiegano con il fatto che lo spettro d'irradianza solare extraterrestre è il risultato del sommarsi di contributi forniti da parti della superficie solare di diversa profondità, principalmente appartenenti alla fotosfera, la cui temperatura di emissione varia tra quella superficiale di poco maggiore di 4000 K e quella più interna che può arrivare a 9000 K, mentre i contributi dovuti alle più calde regioni della cromosfera e della corona solare sono molto meno rilevanti.

Le interazioni della radiazione solare con l'atmosfera

Durante l'attraversamento dell'atmosfera, la radiazione solare subisce una rilevante attenuazione a causa di interazioni (processi di assorbimento e/o di scattering) con numerosi costituenti atmosferici, venendo in parte assorbita e in parte diffusa in tutte le direzioni e raggiungendo, quindi, solo parzialmente la superficie terrestre. Tra i processi di assorbimento, i più importanti sono quelli dovuti ad assorbimento selettivo da parte delle molecole di diversi gas atmosferici, come il vapore acqueo, l'ossigeno, l'ozono e l'anidride carbonica, mentre effetti piuttosto deboli di assorbimento continuo sono prodotti dall'azoto. La radiazione solare subisce un importante processo di diffusione a opera delle molecole d'aria (scattering di Rayleigh) ed è in parte diffusa e in parte assorbita da aerosol e nubi. Questi processi meritano di essere descritti più accuratamente, dato che fanno variare le frazioni di radiazione solare assorbita dall'atmosfera, riflessa dall'atmosfera verso lo spazio e in arrivo alla superficie terrestre, e, quindi, definiscono anche il valore di albedo del sistema superficie-atmosfera, chiaramente diverso da quello dell'albedo superficiale α_s.

Assorbimento del vapor d'acqua. - Il vapore acqueo è presente nell'atmosfera terrestre in concentrazioni che variano ampiamente con la temperatura e l'umidità relativa dell'aria (tab. 1). Infatti, il vapore acqueo non è distribuito in modo uniforme sul pianeta, ma presenta valori di concentrazione di massa per volume unitario d'aria (umidità assoluta) più elevati nell'area equatoriale e molto bassi nelle aree polari, decrescendo rapidamente con l'altezza a tutte le latitudini: mediamente, circa la metà del contenuto colonnare di vapore acqueo (acqua precipitabile) si trova tra il livello del mare e la quota di 1,5 km circa, mentre meno del 5-6% dell'acqua precipitabile si trova al di sopra della quota di 5 km, e meno dell'1% nella stratosfera, al di sopra dei 12 km. In tal modo, si hanno valori di acqua precipitabile compresi tra 4 e 5,6 g cm⁻² nell'area equatoriale, tra 2,5 a 4,4 g cm⁻² nelle regioni prossime ai tropici e valori decrescenti all'aumentare della latitudine fino a scendere anche al di sotto di 0,1 g cm⁻² nelle regioni polari più fredde.

Per effetto di queste variazioni latitudinali e stagionali, lo spettro di assorbimento della radiazione solare da parte del vapore acqueo (incluso l'assorbimento degli ossidrili) è soggetto a variare largamente nel corso dell'anno alle latitudini medio-alte. Come mostra la fig. 2, lo spettro di attenuazione atmosferica della radiazione solare presenta numerose bande di assorbimento del vapore acqueo, la cui intensità aumenta al crescere della lunghezza d'onda dal visibile al medio infrarosso (0,54 ÷3,5 μm): bande di debole assorbimento sono presenti nell'intervallo spettrale 0,54÷0,66 μm, la banda α da 0,69 a 0,74 μm, la banda 0,8 μm da 0,79 a 0,85 μm, la banda ϱστ da 0,87 a 1,01 μm, la banda Φ da 1,08 a 1,21 μm, la banda Ψ da 1,25 a 1,54 μm, la banda Ω da 1,69 a 2,10 μm, la banda X da 2,27 a 2,99 μm e la banda X′ da 2,95 a 3,57 μm. Inoltre, il vapore acqueo produce rilevanti effetti di assorbimento continuo nella finestra atmosferica da 3,5 a 3,9 μm, entro la quale è presente una banda di assorbimento di HDO. A causa di questi marcati effetti di assorbimento selettivo che caratterizzano larghi intervalli dello spettro solare, il vapore acqueo atmosferico è stimato essere responsabile di circa il 70% dell'assorbimento atmosferico della radiazione solare incidente. Questi processi di assorbimento, più intensi all'equatore e piuttosto deboli nelle regioni di alta latitudine, operano come fattori importanti nel definire le condizioni climatiche sul pianeta, favorendo il trasporto di calore in atmosfera, dalle basse alle alte latitudini, alimentando l'evolvere del ciclo idrico del vapore acqueo attraverso i processi di trasporto verticale di calore legati a quelli di evaporazione, condensazione e precipitazione al suolo.

Assorbimento dei gas atmosferici. - Oltre al vapore acqueo, altri costituenti atmosferici concorrono ad assorbire intensamente la radiazione solare. Tra di essi, i più importanti sono: (a) l'ossigeno (O₂), che presenta quattro forti bande di assorbimento nel visibile, centrate a 0,580, 0,629, 0,688 e 0,762 μm e altre quattro bande meno intense, a 0,538, 0,638, 0,697 e 0,771 μm, oltre a due bande più deboli nell'infrarosso, centrate a 1,064 e 1,268 μm, come si può osservare in fig. 2; (b) l'anidride carbonica (CO₂), che presenta due deboli bande centrate a 1,434 e 1,606 μm, nella finestra atmosferica da 1,54 a 1,69 μm compresa tra le bande Ψ e Ω del vapore acqueo e altre bande di maggiore intensità negli intervalli spettrali da 1,93 a 2,08 μm e da 2,55 a 2,80 μm, totalmente coperte dalle bande Ω e X del vapore acqueo; (c) l'ozono (O₃) che presenta il sistema di bande di Huggins (da 0,31 a 0,35 μm), e la banda di Chappuis da 0,45 a 0,78 μm, oltre a una serie di bande minori centrate a 2,70, 3,28 e 3,57 μm; (d) il biossido d'azoto (NO₂), che presenta un'ampia banda di assorbimento caratterizzata da un semicontinuo nell'intervallo spettrale da 0,25 a 0,58 μm; (e) il metano (CH₄), che presenta una banda fondamentale centrata a 3,31 μm, la quale si sovrappone alla banda X′ del vapore acqueo.

Lo scattering di Rayleigh. - Per scattering di Rayleigh s'intende il processo d'interazione tra la radiazione elettromagnetica e una molecola d'aria, che viene rappresentato come un diffusore di forma sferica (dipolo elettrico) avente dimensioni piccole rispetto alla lunghezza d'onda della radiazione incidente (caratterizzata da un campo elettrico che varia periodicamente). In questo modello fisico, si assume che (a) il diffusore e il mezzo non sono conduttori; (b) il mezzo non contiene cariche elettriche libere; (c) le costanti dielettriche del diffusore e del mezzo sono molto simili; (d) l'indice di rifrazione del diffusore non è troppo alto in modo che il prodotto dell'indice di rifrazione per la massa del diffusore sia minore di 1; (e) l'atto di diffusione è indipendente da un dipolo elettrico all'altro. Allora, il campo elettrico diffuso intorno al diffusore è espresso come la somma del campo elettrico incidente e del campo generato dal dipolo: la quantità di radiazione diffusa da un volume unitario d'aria entro un angolo solido unitario orientato in una certa direzione è data dalla funzione angolare rappresentata dal termine 1+cos²Θ, essendo Θ l'angolo di scattering tra la direzione d'incidenza e la direzione di scattering. Per un simile modello, la forma del diagramma angolare di scattering è costituita da due lobi di forma sferica, orientati l'uno nella direzione in avanti e l'altro nella direzione all'indietro.

Il coefficiente di scattering di Rayleigh, relativo a un volume unitario d'aria, risulta essere proporzionale all'inverso della potenza della lunghezza d'onda con esponente eguale a 4,08 alle lunghezze d'onda del visibile: lo spessore ottico di Rayleigh, relativo al percorso verticale atmosferico in un'atmosfera standard, assume un valore di 1,216 alla lunghezza d'onda di 0,30 μm e decresce gradualmente mantenendosi proporzionale alla summenzionata potenza della lunghezza d'onda, fino ad assumere un valore eguale a 8,63×10⁻³ a 1 μm. A causa di questa forte dipendenza spettrale, la componente violetta della luce solare è soggetta a diffusione in una misura circa 14 volte più intensa della componente rossa, determinando il colore celeste del cielo.

Lo scattering e l'assorbimento degli aerosol. - La teoria elettromagnetica di Mie descrive i processi di scattering e assorbimento di un'onda elettromagnetica piana dovuti a una particella sferica, assumendo che il campo di radiazione generato dalla particella sia dato dalla somma di vari campi creati da quadrupoli elettrici, ottopoli e multipoli di ordini successivi. Questa teoria mostra che le particelle di aerosol sono in grado di diffondere e assorbire la radiazione solare in una misura che dipende non solo dalla loro concentrazione nella colonna verticale dell'atmosfera ma anche dal rapporto tra raggio della particella e lunghezza d'onda incidente e dall'indice complesso di rifrazione del materiale di cui la particella è composta. Perciò, la forma del diagramma di scattering di una particella varia in funzione delle dimensioni e della forma delle particelle di aerosol, dipendendo fortemente dalle proprietà fisico-chimiche del materiale particolato.

Una particella di aerosol può essere definita come un insieme di molecole che ha superato le dimensioni minime di qualche decina di Å e che, grazie all'azione delle forze di coesione tra le sue varie parti, riesce a mantenere la propria integrità individuale per un tempo abbastanza lungo. In base alle loro dimensioni, le particelle di aerosol sono comunemente suddivise in: (a) particelle ultrafini, che hanno raggi equivalenti compresi tra 10⁻³ e 5×10⁻² μm; (b) particelle fini, che hanno raggi compresi tra 5×10⁻² e 1,25 μm (chiamate anche particelle di accumulazione); (c) grandi particelle, che hanno raggi compresi tra 1,25 e 5 μm; (d) particelle giganti, che hanno raggi maggiori di 5 μm. Queste classi di particelle presentano ciascuna una o più mode nella distribuzione dimensionale della concentrazione numerica, così da formare complessivamente una distribuzione multimodale dove le concentrazioni di ciascuna moda decrescono rapidamente al crescere delle dimensioni. Numerosi sono i processi naturali che generano gli aerosol, legati al moto ondoso del mare, alle immissioni in stratosfera di gas di origine vulcanica, alle reazioni fisico-chimiche dei terpeni emessi dalle piante, alla mobilizzazione eolica di polveri desertiche, all'ossidazione di anidride solforosa originata da fenomeni di vulcanismo o da processi chimici marini e alla conversione di gas in particelle. Tra i processi antropici, vanno ricordati quelli legati all'impiego di combustibili fossili, agli incendi di foreste e combustione di biomassa, al traffico veicolare, e alle attività agricole di aratura e concimazione dei campi.

A seguito della loro diversa composizione, gli aerosol possono presentare valori alquanto diversi della parte reale e della parte immaginaria dell'indice di rifrazione: la parte reale può assumere nel visibile valori per lo più compresi tra 1,45 e 1,60 nelle particelle di origine urbana e rurale, e tra 1,35 e 1,40 nelle particelle di sale marino e nelle particelle cresciute per condensazione in goccioline, mentre la parte immaginaria presenta valori anche maggiori di 0,1 nelle particelle di tipo urbano, dell'ordine di 10⁻² nelle particelle di tipo rurale, minori di 10⁻⁴ nelle particelle di origine marina e valori molto bassi, dell'ordine di 10⁻⁸, nelle goccioline d'acqua. Le proprietà radiative delle polidispersioni di aerosol colonnare, tra le quali l'albedo di singolo scattering (che definisce la percentuale di radiazione solare che è soggetta a scattering, la percentuale residua venendo assorbita), dipendono strettamente dalla forma della distribuzione multimodale dell'aerosol colonnare e dal suo indice complesso di rifrazione.

Lo scattering e l'assorbimento delle nubi. - Anche le nubi, come gli aerosol, interagiscono con la radiazione solare causando scattering e assorbimento attraverso i processi descritti dalla teoria di Mie, con intensità che dipende, come per gli aerosol, dalla concentrazione numerica delle goccioline di nube e/o dei cristalli di ghiaccio presenti nelle nubi di diversa quota, dalla forma della distribuzione dimensionale multimodale, dall'indice di rifrazione e dagli effetti di scattering multiplo che hanno luogo all'interno della nube, contribuendo generalmente ad abbassare le caratteristiche di albedo della nube. La concentrazione numerica delle goccioline di nube può variare ampiamente da meno di 10 a più di 10³ goccioline di nube per cm³ d'aria, a seconda del tipo e della quota della nube. La forma della distribuzione dimensionale varia largamente con il tipo di nube (cumuliforme, stratiforme, a cirro), e quindi, con la quota e le condizioni di temperatura all'interno della nube, potendo coprire un ampio intervallo del raggio, da meno di 1 mm (goccioline in fase di formazione) a più di 800 mm (cristalli di ghiaccio a crescita dendritica). L'indice di rifrazione dell'acqua liquida assume valori della parte reale prossimi a 1,33 nel visibile e crescenti da 1,35 a 1,60 nel vicino e medio infrarosso, mentre la parte immaginaria assume valori al di sotto di 10⁻⁴ nel visibile e valori tra 10⁻⁴ e 5×10⁻¹ nel vicino e medio infrarosso. Invece, la parte reale dell'indice di rifrazione del ghiaccio assume valori prossimi a 1,3 nel visibile e vicino infrarosso e valori leggermente più bassi intorno a 1,2 nel medio infrarosso, mentre la parte immaginaria cresce gradualmente da valori minori di 10⁻⁶ nel visibile a valori compresi tra 10⁻² e 10⁻¹ nel medio infrarosso. Le caratteristiche di riflettanza delle nubi, risultanti dagli effetti combinati di scattering singolo e multiplo così come da quelli di assorbimento interno alla nube, possono dipendere non solo dalla concentrazione numerica delle goccioline di nube o dei cristalli di ghiaccio ma anche dallo spessore geometrico della nube, variando l'albedo delle nubi tra pochi percento nel caso di nubi sottili (aventi spessore di poche decine di metri) a valori prossimi a 1 per spessori dell'ordine di 1 km, anche quando le concentrazioni delle goccioline sono relativamente basse (∼200 cm⁻³).

La radiazione terrestre

fig. 4

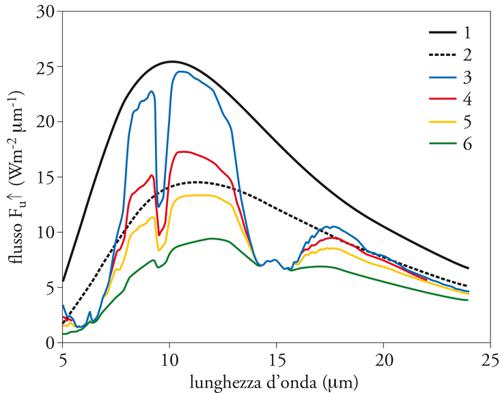
Riscaldata dall'assorbimento di una parte della radiazione solare che riesce ad attraversare l'atmosfera, la superficie terrestre emette radiazione infrarossa secondo una curva di distribuzione spettrale avente la forma della [1], nella quale T è la temperatura equivalente di corpo nero. Le curve spettrali della radianza infrarossa emessa da due corpi neri alle temperature di 288 K (relativa alla superficie terrestre: curva 1) e di 255 K (relativa alla temperatura media della troposfera: curva 2) sono presentate in fig. 4 e confrontate con la curva spettrale di radianza infrarossa emessa dal sistema superficie-atmosfera verso lo spazio, per condizioni standard dell'atmosfera definite dal modello atmosferico U. S. Standard Atmosphere 1976 avente il valore di acqua precipitabile W=1,44 g cm⁻² e visibilità al suolo di 23 km (curva 3). Negli intervalli spettrali 5÷8 μm e 13÷17 μm, occupati dalle bande di H₂O e CO₂, rispettivamente, la curva spettrale di F_u↑ emesso dall'atmosfera standard presenta valori più bassi di quelli corrispondenti alla temperatura di 255 K, in quanto la radianza emessa dalla superficie e dalla bassa atmosfera è totalmente assorbita dall'atmosfera sovrastante e il solo contributo della parte superiore dell'atmosfera raggiunge lo spazio, avendo temperature di emissione più vicine a quella di tropopausa. Invece, all'interno dell'intervallo di lunghezza d'onda 8÷13 μm, fatta eccezione per lo stretto intervallo spettrale occupato dalla banda di ozono, i valori di F_u↑ sono molto vicini a quelli di corpo nero a 288 K, in quanto il massimo contributo è dato dalla superficie terrestre (debolmente attenuato dall'atmosfera) e l'atmosfera fornisce solo un contributo alquanto basso a causa della sua bassa emissività (e assorbitività) in quell'intervallo spettrale. Infatti, per meglio comprendere che la distribuzione spettrale della densità di flusso uscente F_u↑ varia in funzione delle concentrazioni atmosferiche medie dei gas atmosferici che assorbono nell'infrarosso, si deve tener presente che tale flusso consiste di due componenti: (a) la prima, data dalla radianza emessa dalla superficie, che è piuttosto elevata nella finestra di trasparenza atmosferica da 8 a 13 μm e del tutto trascurabile dentro gli intervalli spettrali occupati dalle bande di assorbimento del vapore acqueo (H₂O), anidride carbonica (CO₂), ozono (O₃) e metano (CH₄) a causa della sua attenuazione totale da parte dell'atmosfera, (b) la seconda, data dai contributi forniti dai diversi strati atmosferici che emettono radianza termica verso l'alto, la quale è attenuata solo dalla parte soprastante dell'atmosfera. L'emissione di radianza termica da parte della superficie terrestre ha luogo in accordo con le [1], [2] per valori dell'emittanza ε_s compresi tra 0,92 e 0,98 nei diversi intervalli spettrali e per i vari tipi di superficie. L'atmosfera emette anch'essa come un corpo grigio con caratteristiche di emittanza che variano in funzione dell'altezza, più alta nella bassa troposfera e via via più bassa all'aumentare della quota, in quanto ogni strato di atmosfera ha l'emittanza eguale all'assorbanza (principio di Kirchhoff), l'assorbanza dipendendo dalla concentrazione dei gas assorbenti presenti in uno strato atmosferico e dall'intensità spettrale dei processi di assorbimento. Poiché la densità dell'atmosfera diminuisce con l'altezza, ne consegue che l'emittanza atmosferica decresce all'aumentare dell'altezza, presentando valori più elevati negli intervalli spettrali caratterizzati da forte assorbimento selettivo.

Le interazioni della radiazione terrestre con l'atmosfera

La precedente fig. 2 mostra lo spettro di radianza emessa dal sistema superficie-atmosfera verso lo spazio, per condizioni termodinamiche standard dell'atmosfera, mettendo in evidenza gli effetti di assorbimento prodotti dalle bande di H₂O, CO₂ e O₃. Questi processi di assorbimento che caratterizzano lo spettro della radianza terrestre sono i più evidenti ma numerose altre bande di più debole intensità contribuiscono ad assorbire la radianza emessa dalla superficie terrestre e dall'atmosfera e altri effetti di scattering e assorbimento da parte degli aerosol e delle nubi contribuiscono ad attenuare la radianza terrestre e quella emessa dai vari strati atmosferici verso l'alto e verso il basso. Questi processi di interazione della radiazione infrarossa con l'atmosfera meritano di essere descritti accuratamente, al fine di capire in che modo i vari costituenti atmosferici contribuiscono a emettere radianza verso l'alto e verso il basso.

fig. 5

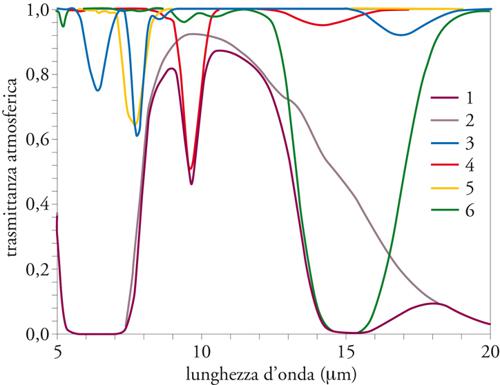
L'assorbimento del vapore acqueo e degli altri gas-serra. - Al fine di dare un'idea dell'intensità dei processi di assorbimento della radianza infrarossa da parte dei diversi gas atmosferici, la fig. 5 mostra la curva spettrale della trasmittanza atmosferica totale definita per il modello atmosferico U. S. Standard Atmosphere 1976 e le curve di trasmittanza parziale del vapore acqueo, dell'ozono, dell'anidride carbonica, del metano e della miscela di gas N₂O+O₂+CO. Tale confronto mette in evidenza il sovrapporsi dei diversi effetti di assorbimento prodotti dalle più forti bande molecolari nell'intervallo di lunghezza d'onda 5÷20 μm. Il vapore acqueo presenta la forte banda vibro-rotazionale ν₂ estendentesi da 4,8 a 8,2 μm e la banda rotazionale che copre l'intervallo spettrale da 20 a 500 μm, producendo effetti apprezzabili anche da 16 a 20 μm; inoltre, tutto l'infrarosso è interessato da effetti di assorbimento continuo, dovuto sia alle molecole di acqua che ai dimeri e ai polimeri di ordine superiore dell'acqua. La CO₂ presenta la forte banda vibro-rotazionale ν₂ estendentesi da 13,3 μm a 17,4 μm, con massimo assorbimento tra 14,8 e 15,0 μm, oltre alla debole banda 3ν₂ centrata a 5,2 μm, e le ancor più deboli bande centrate a 9,4 e a 10,4 μm, che appaiono posizionate ai lati della banda ν₃ dell'ozono, dalla quale sono nascoste quasi completamente. Infatti, l'ozono presenta la banda ν₃ estesa da 8,75 a 10,30 μm che appare in tutta evidenza in fig. 3, al centro della finestra da 8 a 13 μm, oltre alla debole banda centrata a 14,1 μm, che si sovrappone totalmente alla banda ν₂ della CO₂. Altre bande d'intensità medio-debole sono presentate dal metano (banda ν₄ centrata a 7,66 μm, che si sovrappone alla banda ν₂ del vapore acqueo) e dal protossido d'azoto (bande centrate a 7,78 e 16,98 μm, che si sovrappongono alle più forti bande ν₂ di H₂O e CO₂, rispettivamente). I clorofluorometani CFC e gli HCFC presentano una grande numero di bande nell'intervallo spettrale da 6 a 20 μm, tutte caratterizzate da elevati valori dei coefficienti di assorbimento ma capaci di produrre solo limitati effetti di assorbimento sullo spettro della radianza atmosferica (effetto serra), in quanto queste specie molecolari sono presenti in atmosfera in bassissime concentrazioni.

Per effetto di questi processi di assorbimento, l'atmosfera impedisce che una gran parte della radianza termica emessa dalla superficie terrestre raggiunga lo spazio ma assorbendola intrappola questa radiazione dentro il sistema, producendo il cosiddetto effetto serra, che garantisce che la temperatura media di equilibrio alla superficie sia di circa 288 K e permette di avere condizioni favorevoli di vita nella maggior parte del pianeta. Le valutazioni di densità di flusso uscente F_u↑ mostrate in fig. 2 indicano chiaramente che il principale gas-serra è il vapore acqueo, e che gli altri gas-serra sono nell'ordine la CO₂, il CH₄ e l'N₂O. La concentrazione media globale di CO₂ è aumentata rapidamente passando da 280 ppmv nel 1750 a 330 ppmv negli anni Settanta del Novecento, e salendo negli ultimi 40 anni a 380 ppmv, come risulta dalle misure effettuate recentemente presso le numerose stazioni del World Data Centre Greenhouse Gases (WDCGG). Si valuta che l'aumento della concentrazione media globale di questo gas abbia prodotto una forzatura radiativa media di 1,5 Wm⁻² sulla scala globale, rispetto al periodo preindustriale. La concentrazione media di CH₄ ha raggiunto valori compresi tra 1700 e 1850 ppbv nelle stazioni della rete mondiale WDCGG, con una forzatura media maggiore di 0,5 Wm⁻² rispetto al periodo preindustriale. La concentrazione media di N₂O ha raggiunto valori intorno ai 310 ppbv in diverse stazioni della rete WDCGG, che si stima dia una forzatura radiativa media globale di circa 0,1 Wm⁻².

Lo scattering e l'assorbimento degli aerosol e delle nubi. - I processi di interazione della radiazione a onda lunga con gli aerosol presenti in atmosfera e con le nubi possono essere descritti realisticamente dalla teoria elettromagnetica di Mie. Anche gli effetti di scattering e assorbimento della radiazione infrarossa dipendono strettamente dalla concentrazione delle particelle di aerosol e delle nubi, dalla forma della distribuzione dimensionale di queste particelle e dall'indice complesso di rifrazione che definisce le loro proprietà radiative. Gli indici di rifrazione delle particelle di aerosol e delle particelle di nube nell'infrarosso variano apprezzabilmente sia nella loro parte reale (che assume valori compresi per lo più tra 1,8 e 2,2 per gli aerosol, tra 1,35 e 2,30 per l'acqua liquida e intorno a 1,2 per il ghiaccio) sia nella loro parte immaginaria (che presenta valori compresi tra 0,002 e 0,3 nelle particelle di aerosol di diversa origine, tra 0,02 e 0,5 per le goccioline d'acqua e tra 0,01 e 0,1 per i cristalli di ghiaccio). Gli effetti radiativi degli aerosol sono in generale assai deboli nell'infrarosso, dato che il rapporto tra dimensioni delle particelle e lunghezza d'onda cambia di un fattore 10÷30 passando dal visibile all'infrarosso, mentre le caratteristiche di riflettanza e assorbanza delle nubi sono alquanto simili per tutti i tipi di nube, essendo il rapporto tra raggio delle goccioline e lunghezza d'onda considerevolmente più grande che nel visibile. Le caratteristiche di trasmittanza, assorbanza ed emittanza delle nubi dipendono sostanzialmente dallo spessore della nube e dalla concentrazione di goccioline o di cristalli di ghiaccio, essendo i parametri di forma della distribuzione dimensionale quasi del tutto ininfluenti. La radianza emessa dalle nubi dipende fortemente dalla temperatura di emissione della nube, come mostra la fig. 4, che presenta un confronto tra le curve spettrali di radianza emessa verso lo spazio da due corpi neri alle temperature di 288 e 255 K e le curve spettrali di radianza uscente da un'atmosfera standard, nella quale si simula la presenza di tre strati di nube di tipo diverso, aventi tutti e tre uno spessore ottico di 3,6 nel visibile: (a) uno strato di nube di tipo cumuliforme con spessore geometrico di 2 km che si estende da 2 a 4 km di quota, con una temperatura di 262,2 K alla quota di 4 km; (b) uno strato di nube a stratocumulo, dello spessore di 1 km ed estesa da 5 a 6 km di quota, dove la temperatura è eguale a 249,2 K; (c) una nube a cirro dello spessore di 0,5 km, che si trova tra 8 e 8,5 km, con temperatura della faccia superiore eguale a 233 K. Si può notare agevolmente come la densità di flusso F_u↑ assuma valori molto simili negli intervalli occupati dalle bande di H₂O e CO₂, in quanto la radianza uscente è emessa principalmente dalla parte superiore dell'atmosfera, e presenti valori strettamente dipendenti dalla temperatura della faccia superiore delle nubi nell'intervallo di trasparenza atmosferica da 8 a 13 μm.

Il bilancio di radiazione del sistema Terra-atmosfera

Il bilancio di radiazione della Terra (sistema superficie-atmosfera) è dato dalla somma

[6] B = B_s + B_a

dove B_s è il bilancio di radiazione alla superficie terrestre e B_a è il bilancio di radiazione dell'atmosfera.

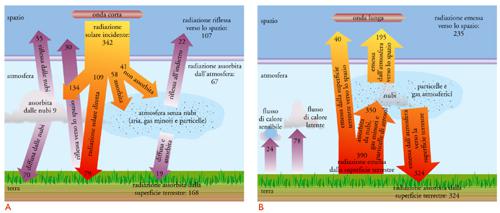
Il sistema superficie-atmosfera tende a mantenersi in ogni istante in equilibrio radiativo con lo spazio esterno alla Terra, passando da una configurazione di equilibrio all'altra attraverso scambi di radiazione tra il sistema e lo spazio esterno. Considerando che la densità di flusso Q* della radiazione solare incidente è eguale a un quarto della costante solare S_⊗ (ovvero a 342 Wm⁻²), si deve tener conto che l'atmosfera attenua fortemente la radiazione solare in arrivo e che solo una parte della radiazione solare incidente riesce a raggiungere la superficie terrestre. Infatti, si valuta che la radiazione solare entrante interagisca con le nubi, nella misura media del 39% (134 Wm⁻²) e con l'atmosfera senza nubi (scattering di Rayleigh, gas e aerosol), nella misura del 29% (99 Wm⁻²), mentre solo la parte restante pari al 32% (109 Wm⁻²) raggiunge la superficie terrestre: di questa frazione, solo il 28% (30 Wm⁻²) viene riflesso verso lo spazio e il restante 72% (79 Wm⁻²) è assorbito dalla superficie terrestre. Della frazione di radiazione solare che interagisce con l'atmosfera senza nubi (99 Wm⁻², pari al 29% di Q*), il 59% circa (58 Wm⁻²) è assorbito dall'atmosfera, principalmente dal vapore acqueo, e il 41% circa (41 Wm⁻²) viene diffuso dall'atmosfera verso il basso, venendo assorbito dalla superficie oppure verso l'alto (19 Wm⁻²) fino a raggiungere lo spazio esterno (22 Wm⁻²). Il 39% di Q* (134 Wm⁻²) interagisce con le nubi, del quale il 7% circa (9 Wm⁻²) viene assorbito dalle nubi, il 52% circa (70 Wm⁻²) viene diffuso dalle nubi verso il basso e successivamente assorbito dalla superficie, e 41% circa (55 Wm⁻²) è diffuso verso l'alto, fino a raggiungere lo spazio esterno.

Si valuta che la superficie terrestre emetta verso l'alto un flusso medio annuo di radianza infrarossa eguale a 390 Wm⁻². Di questa radianza superficiale, una parte pari al 10% circa (40 Wm⁻²) raggiunge direttamente lo spazio esterno, principalmente entro la finestra atmosferica da 8 a 13 μm, e la parte restante del 90% (350 Wm⁻²) è assorbita dall'atmosfera terrestre attraverso interazioni con le nubi, il vapore acqueo e gli altri gas-serra. Assorbendo la radiazione infrarossa proveniente dal basso, l'atmosfera terrestre si riscalda ed emette a sua volta radiazione infrarossa verso il basso e verso l'alto. Dato che la temperatura dell'aria diminuisce al crescere dell'altezza in tutta la troposfera e che la faccia superiore di ogni tipo di nube è più fredda di quella inferiore, l'atmosfera emette più radiazione verso il basso, cedendola alla superficie, che non verso l'alto e lo spazio: per questo, si ottiene un valore di 324 Wm⁻² per la densità di flusso diretta verso il basso e un valore più basso, eguale a 195 Wm⁻², per quella diretta verso l'alto.

Il bilancio di radiazione alla superficie. - Nel bilancio di radiazione B_s, i guadagni (di segno positivo) sono dati dai termini di densità di flusso complessivo delle componenti diretta e diffusa della radiazione solare, che sono assorbite dalla superficie terrestre e dalle densità di flusso della radiazione infrarossa emessa dall'atmosfera verso il basso e assorbita dalla superficie terrestre. Le perdite (di segno negativo) sono date dalla sola densità di flusso della radiazione a onda lunga che la superficie terrestre emette verso l'alto. Pertanto, il bilancio B_s può essere scritto nella forma seguente

[7] B_s = (Q_s+q_s)(1−α_s) + A_sL_a↓ − L_s↑

dove Q_s è la densità di flusso della radiazione solare diretta in arrivo alla superficie; q_s è la densità di flusso della radiazione solare diffusa che raggiunge la superficie terrestre, originata dalle molecole d'aria, dalle particelle di aerosol e dalle nubi; α_s è l'albedo media della superficie terrestre per la radiazione solare, tale parametro dipendendo non solo dalla natura della superficie ma anche dalle distribuzioni spettrali dei termini Q_s e q_s; A_s è l'assorbitività media della superficie terrestre per la radiazione a onda lunga; L_a↓ è la densità di flusso della radiazione a onda lunga che viene emessa dall'atmosfera verso il basso e che raggiunge la superficie terrestre; L_s↑ è la densità di flusso della radiazione a onda lunga che viene emessa dalla superficie terrestre verso l'atmosfera.

Tav. I A

Secondo le stime mostrate nella Tav. I A, il termine Q_s (1−α_s) che compare nella [7] risulta essere mediamente eguale a 79 Wm⁻², mentre il termine q_s (1−α_s) è eguale a 89 Wm⁻², comprendendo insieme il contributo della radiazione solare diffusa dalle nubi e quello dovuto allo scattering di Rayleigh e agli aerosol (atmosfera senza nubi). Nella Tav. I B, il termine in perdita della radiazione a onda lunga è stimato assumere il valore L_s↑= 390 Wm⁻² e quello in guadagno è dato da A_s L_a↓=324 Wm⁻². Ne consegue che B_s risulta essere positivo, dato che la superficie terrestre riceve mediamente 168 Wm⁻² in forma di radiazione solare e perde 66 Wm⁻² in forma di radiazione a onda lunga: il guadagno complessivo è stimato in 102 Wm⁻². Queste condizioni di bilancio positivo della radiazione alla superficie terrestre indicano che la superficie terrestre sarebbe destinata a riscaldarsi, se non vi fossero altri processi di trasporto di energia di segno opposto dalla superficie terrestre verso l'atmosfera.

Il bilancio di radiazione dell'atmosfera. - I termini di guadagno del bilancio di radiazione B_a (relativo all'atmosfera) sono dati dalle densità di flusso relative alle componenti diretta (Q_a) e diffusa (q_a) della radiazione solare assorbite dall'atmosfera e dalla densità di flusso L_A↑ della radiazione a onda lunga che viene emessa dalla superficie terrestre verso l'alto, venendo successivamente assorbita dall'atmosfera. Le perdite che compaiono in B_a sono date dalla densità di flusso L_a↓ della radiazione a onda lunga che viene emessa dall'atmosfera verso il basso, raggiungendo la superficie terrestre, e dalla densità di flusso L_a↓ della radiazione a onda lunga che è emessa dall'atmosfera verso l'alto e raggiunge lo spazio esterno. Allora, il bilancio B_a può essere scritto nella forma seguente:

[8] B_a = Q_a + q_a + L_A↑ − L_a↓ − L_A↑.

Secondo le stime presentate nella Tav. I A e B, il bilancio di radiazione B_a dell'atmosfera, definito nella [8], consiste (a) del guadagno dato dalla somma Q_a+q_a relativa alla radiazione solare diretta e diffusa assorbita dall'atmosfera, stimato essere mediamente eguale a 67 Wm⁻², con 9 Wm⁻² assorbiti dalle nubi e 58 Wm⁻² dai gas atmosferici (vapore acqueo principalmente); (b) di un termine di guadagno medio L_A↑=350 Wm⁻²; (c) di un termine medio di perdita L_a↓=324 Wm⁻²; (d) di un termine medio di perdita L_a↓=195 Wm⁻², dovuto alla radianza a onda lunga emessa dall'atmosfera verso lo spazio. Sommando questi termini, si ottiene che il bilancio medio globale di radiazione nell'atmosfera è dato da B_a=−102 Wm⁻², indicando come l'atmosfera subisca complessivamente una perdita di radiazione, principalmente a causa dell'effetto serra che concorre a trasferire radiazione alla superficie, riscaldandola, e in minor misura a causa dell'emissione verso lo spazio esterno.

Il bilancio di radiazione del sistema superficie-atmosfera. - Tornando alla [8] e indicando con τ_a la trasmittanza totale dell'atmosfera per la radiazione a onda lunga, si può scrivere che

[9] L_A↑ = (1−τ_a)L_s↑

dove il termine di flusso L_s↑ è definito dalla [7]. Allora, si ottiene dalle [6], [7],[8] e [9] che il bilancio radiativo totale B del sistema Terra-atmosfera può essere scritto nella forma seguente:

[10] B = (Q_s+ q_s)(1−α_s) + Q_a + q_a + A_sL_a↓ − L_s↑ +

+ L_s↑ − τ_aL_s↑ − L_a↓ − L_a↑.

Tenendo conto dei concetti di flusso entrante Φ_e e di densità di flusso uscente F_u↑ definiti nelle [3] e [4] e considerato il fatto che la densità di flusso Q* è eguale a S_⊗/4 quando la si confronta con la quantità F_u↑ per verificare l'esistenza delle condizioni di equilibrio radiativo del sistema, è possibile sostituire la somma dei termini a onda corta che entrano nel bilancio di radiazione della Terra nella [10] con il termine

[11] Q*(1−α) = (Q_s + q_s)(1−α_s) + Q_a + q_a

dove α è l'albedo media del sistema, comprendente gli effetti combinati della superficie e dell'atmosfera, che può essere definita come la percentuale di radiazione solare riflessa all'indietro dal sistema superficie-atmosfera, dipendendo quindi dalle caratteristiche di riflettanza superficiale, dall'intensità dello scattering di Rayleigh, dalle proprietà di scattering e assorbimento degli aerosol e delle nubi, e dalle proprietà di assorbimento dei gas atmosferici. Le stime di densità di flusso della radiazione solare date nella Tav. I A determinano un valore di α=0,313. Allora, la grandezza Q*(1−α) definita nella [11] rappresenta la frazione di radiazione solare che riesce effettivamente a entrare nel sistema Terra e la [10] può essere scritta nella forma seguente:

[12] B = Q*(1−α) − (1−A_s)L_a↓ − (τ_aL_s↑ + L_a↑).

Ma tenendo conto che l'assorbitività A_s assume un valore intorno a 0,98, molto vicino a 1, il termine (1−A_s)L_a↓ può essere trascurato rispetto alla densità di flusso F_u↑ che rappresenta, in pratica, la densità di flusso della radiazione a onda lunga uscente dal sistema Terra-atmosfera. Allora, si trova che è

[13] F_u↑ = τ_aL_s↑ + L_a↑

e la [12] assume la forma finale

[14] B = Q*(1−α) − F_u↑.

fig. 6

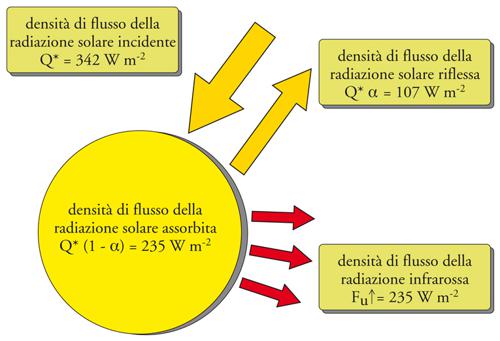
Pertanto, considerando tutto il sistema Terra-atmosfera, il bilancio di radiazione al vertice dell'atmosfera è dato dalla differenza tra la densità di flusso della radiazione solare incidente, eguale a Q*=S_⊗/4=342 Wm⁻², e la somma dei termini Q*α e F_u↑. Il termine Q*α è dato dalla somma di tre contributi, dei quali (a) il primo dovuto alla riflessione della radiazione solare da parte della superficie terrestre e non assorbito dall'atmosfera nel passaggio di ritorno verso lo spazio (30 Wm⁻²); (b) il secondo prodotto dallo scattering di Rayleigh e degli aerosol, complessivamente eguale a 22 Wm⁻², dei quali non più del 10% è attribuibile agli aerosol sulla scala globale; (c) il terzo dovuto alla riflessione della radiazione solare da parte delle nubi (55 Wm⁻²). Pertanto, il prodotto Q*α assume il valore medio positivo di 107 Wm⁻², dal quale si ricava α=0,313. Il valore medio del parametro F_u↑ a onda lunga va definito, in accordo con la [13], come somma di due contributi, dei quali il primo termine è τ_aL_s↑, dato dalla radianza infrarossa emessa dalla superficie e capace di raggiungere lo spazio, valutato assumere un valore medio globale di 40 Wm⁻²; e il secondo è L_a↑, dato dalla radianza infrarossa emessa dall'atmosfera verso lo spazio, stimato essere mediamente eguale a 195 Wm⁻². Si ottiene che la densità di flusso della radiazione infrarossa uscente dal sistema è mediamente eguale a 235 Wm⁻². Sommando il termine di flusso uscente di radiazione solare eguale a Q*α con quello di flusso uscente F_u↑, si trova il valore totale di 342 Wm⁻² che è equale e di segno opposto alla densità di flusso incidente Q*, come mostra lo schema di fig. 6.

Il ruolo dell'effetto serra nel bilancio di radiazione della Terra

Tav. II

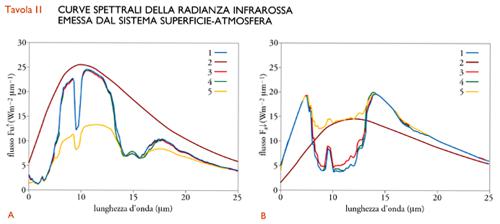
La fig. 4 mostra chiaramente che la maggior parte della radiazione a onda lunga emessa dal sistema Terra-atmosfera verso lo spazio esterno appartiene agli intervalli spettrali occupati dalle bande di H₂O e CO₂, che limitano la finestra atmosferica da 8 a 13 μm. In questo intervallo spettrale, la trasmittanza atmosferica τ_a può presentare considerevoli variazioni se i contenuti medi di vapor d'acqua, CO₂ e altri gas-serra aumentano nel tempo. Volendo dare la misura della rilevanza di questi effetti sul bilancio di radiazione della Terra, nella Tav. II sono mostrate le curve spettrali della radianza infrarossa emes-sa dall'atmosfera verso lo spazio (Tav. II A) e verso il basso (Tav. II B), rispettivamente, nel caso che l'atmosfera presenti condizioni standard di pressione, temperatura e umidità. Queste curve sono confrontate con quelle analoghe ottenute, la prima, per un aumento del contenuto atmosferico del vapore acqueo pari al 20% e, la seconda, per un raddoppio delle concentrazioni di CO₂ e CH₄ rispetto a quelle registrate negli anni Settanta. La Tav. I B mostra che questo aumento di concentrazione provoca una diminuzione complessiva del flusso uscente F_u↑, principalmente dovuta all'assorbimento continuo del vapore acqueo (osservabile tra 8 e 13 μm) e all'assorbimento delle ali della banda ν₂ della CO₂. Si valuta dai dati di Tav. II A che tale diminuzione, associata al raddoppio delle concentrazioni di CO₂ e CH₄, sia di 3,6 Wm⁻². La Tav. II B conferma che le bande di H₂O e CO₂ forniscono un importante contributo alla densità di flusso F_a↓, mostrando che l'aumento del contenuto atmosferico di vapore acqueo del 20% non determina apprezzabili variazioni dentro le bande di assorbimento ma produce, invece, un marcato aumento della radianza nella finestra da 8 a 13 μm, principalmente per effetto dell'assorbimento continuo del vapor d'acqua. Il raddoppio delle concentrazioni di CO₂ e CH₄ produce sensibili aumenti nell'ala di destra della banda di H₂O, in corrispondenza della banda del metano, nel centro della finestra, in corrispondenza della debole banda di CO₂ a 10,4 μm, e lungo entrambe le ali della banda vibro-rotazionale ν₂ della CO₂. L'aumento complessivo di F_a↓ dovuto al raddoppio di concentrazione media globale di questi due gas-serra è stimata in 4,3 Wm⁻²: questa stima appare essere del tutto realistica, se si pensa che le valutazioni dell'aumento di F_a↓ (effetto serra) prodotto dagli aumenti delle concentrazioni dei gas-serra dal 1750 (era preindustriale) al 2000 sono state stimate dall'IPCC (Intergovernmental panel on climate change) intorno a 1,6 Wm⁻² per l'aumento della CO₂, 0,5 Wm⁻² per l'aumento del CH₄, 0,2 Wm⁻² per l'aumento dell'N₂O e 0,3 Wm⁻² per l'aumento dei CFC e degli HCFC, fornendo una stima complessiva della forzatura radiativa (producente riscaldamento globale) pari a circa 2,4 Wm⁻².

A causa della diminuzione di F_u↑, associata a tale forte incremento dell'effetto serra di CO₂ e CH₄, il termine F_u↑ scenderebbe a poco più di 231 Wm⁻² nello schema di fig. 5, e il bilancio di radiazione B risulterebbe di conseguenza sbilanciato, assumendo un valore positivo di 3,6 Wm⁻² a causa del prevalere del flusso entrante di radiazione solare. Ciò comporterebbe un riscaldamento tale dell'atmosfera terrestre da far aumentare gradualmente il termine di flusso F_u↑ fino a ristabilire l'equilibrio con il flusso entrante di radiazione a onda corta.

Le figg. A e B della Tav. II mostrano anche le variazioni delle curve spettrali della radianza infrarossa emessa verso l'alto e verso il basso, nel caso che sia presente in atmosfera una nube stratiforme estesa da 5 a 6 km di quota. Tenendo presenti le stesse considerazioni fatte commentando i risultati di fig. 2, si può notare come la curva di radianza emessa verso l'alto presenta, nella finestra 8÷13 μm, dei valori spettrali che sono dati dalla somma del contributo emesso dalla superficie (e moderatamente attenuato dall'atmosfera) e di quello fornito dalla radianza emessa dalla nube (e solo debolmente attenuato dall'atmosfera). Invece negli intervalli spettrali dominati dal forte assorbimento dei gas atmosferici il contributo superficiale è praticamente nullo e il contributo della nube presenta valori strettamente legati alla temperatura della faccia superiore della nube, in quanto l'attenuazione atmosferica della radianza della nube è alquanto modesta. Similmente, considerando la curva di radianza emessa dall'atmosfera verso il basso, in presenza della nube (fig. 6), risulta evidente come i valori spettrali di questo flusso dipendano principalmente dalla temperatura di emissione della faccia inferiore della nube.

Se la nube si trovasse a bassa quota, la temperatura del suo strato superiore non sarebbe molto diversa dalla temperatura superficiale: in questo caso, la nube provocherebbe solo piccole variazioni in F_a↓. Nel caso, invece, che la nube si trovasse ad alta quota, la temperatura del suo strato superiore sarebbe considerevolmente più bassa di quella della superficie terrestre: in questo caso, la nube indurrebbe una considerevole diminuzione di F_a↓ e influenzerebbe scarsamente il termine F_u↑.

Il ruolo delle nubi sul bilancio di radiazione alla superficie, in atmosfera e al vertice dell'atmosfera, deve però essere valutato tenendo anche conto delle variazioni indotte direttamente dalle nubi sull'albedo del sistema superficie-atmosfera: in generale, si può affermare che l'effetto complessivo prodotto dalle nubi è di raffreddamento da parte delle nubi di bassa e media quota (essendo prevalenti gli effetti di albedo su quelli di emissione di radiazione infrarossa) e di riscaldamento da parte delle nubi di alta quota, dato che queste ultime concorrono a far diminuire apprezzabilmente il termine F_u↑ di radiazione infrarossa.

Il bilancio di calore del sistema superficie-atmosfera

Le valutazioni medie dei termini di bilancio B_s e B_a fatte nelle figg. 6 e 7 mostrano chiaramente che B_s è positivo, presentando un valore medio eguale a 102 Wm⁻² e B_a è negativo, presentando un valore medio eguale a −102 Wm⁻². Ma la Tav. I B mostra anche che questa situazione di squilibrio è compensata da due importanti processi di trasporto di calore dalla superficie terrestre all'atmosfera, i quali riportano in equilibrio il bilancio netto di energia alla superficie terrestre e il bilancio netto di energia dell'atmosfera. Essi sono: (a) il trasporto di calore latente, relativo ai processi di evaporazione e condensazione che portano alla formazione delle nubi, che fornisce un valore medio annuo della densità di flusso di calore C=78 Wm⁻²; (b) il trasporto di calore sensibile per flusso turbolento, che è solitamente limitato allo strato limite dell'atmosfera e fornisce un valore medio annuo della densità di flusso di calore P=24 Wm⁻². Attraverso questi processi di scambio di calore, la quantità di radiazione che viene assorbita in eccesso dalla superficie terrestre è restituita all'atmosfera attraverso il flusso di calore latente e il flusso di calore sensibile. Il primo processo è legato al ciclo evaporazione-condensazione dell'acqua e contribuisce efficacemente al trasporto di calore dalla superficie all'atmosfera: parte del calore guadagnato dai terreni umidi, dai laghi e dai fiumi e, principalmente, dagli oceani per assorbimento di radiazione viene speso in evaporazione. II vapor d'acqua trasporta in atmosfera energia in forma di calore latente che viene restituito all'aria circostante quando ha luogo la condensazione, con conseguente formazione della nube. Il secondo processo di trasporto avviene attraverso un flusso turbolento di calore sensibile dalla superficie terrestre all'atmosfera, che si manifesta in modo evidente quando la temperatura si riscalda per assorbimento della radiazione solare. In tal modo, una parte del guadagno radiativo della litosfera viene speso in calore sensibile ceduto all'atmosfera e una parte viene invece ceduta al terreno sottostante, in modo tale da favorire l'instaurarsi di un flusso di calore verso gli strati più interni della litosfera. Questo processo di trasferimento di calore sensibile avviene anche all'interfaccia idrosfera-atmosfera, in quanto parte dell'energia radiativa rimane assorbita in forma di calore sensibile nello strato superficiale dell'acqua.

Le variazioni latitudinali delle componenti del bilancio termico

Le stime della densità di flusso entrante Q*(1−α) di radiazione solare, della densità di flusso uscente F_u↑ di radiazione infrarossa e del bilancio totale B, definite nella [14] e fatte a diverse latitudini, indicano chiaramente che queste grandezze fisiche aumentano largamente passando dalle regioni polari all'equatore (0°). Infatti, Q*(1−α) aumenta mediamente da 66 Wm⁻² (a 90 °N) a più di 260 Wm⁻² (0°), F_u↑ da circa 170 Wm⁻² (90 °N) a 240 Wm⁻² (0°) e il bilancio B da −100 Wm⁻² (90 °N) a 40 Wm⁻² (0°). Queste stime mostrano anche che il bilancio B assume valori negativi alle latitudini elevate, denotando l'esistenza di una situazione di deficit che decresce gradualmente all'aumentare della latitudine fino a svanire alle latitudini medie (intorno ai 35÷40 gradi di latitudine in entrambi gli emisferi) per lasciare posto a una situazione di surplus alle latitudini più prossime all'equatore. Questo andamento è dovuto al fatto che la radiazione solare illumina la Terra secondo angoli d'incidenza che variano nel corso della giornata e nel corso dell'anno e con intensità sensibilmente più elevata alle basse latitudini. Dato che il sistema superficie-atmosfera emette radiazione infrarossa verso lo spazio in una misura che dipende strettamente dalle condizioni termiche del sistema, accade che Q*(1−α) prevalga su F_u↑ alle basse/medie latitudini e che avvenga il contrario alle latitudini più elevate. Le valutazioni fatte attraverso l'analisi dei dati satellitari confermano questa forte variabilità del bilancio B in funzione della latitudine, che risulta presentare valori di deficit spesso al di sotto dei −100 Wm⁻² alle alte latitudini (mediamente di −125 Wm⁻² al Polo Nord e di −100 Wm⁻² al Polo Sud) e valori positivi, talvolta maggiori di +80 Wm⁻², alle latitudini prossime all'equatore. Allontanandosi dall'equatore, il bilancio B tende ad assumere valori gradualmente decrescenti fino ad assumere valori nulli alle medie latitudini, dove prevalgono i processi di emissione di radiazione termica su quelli di assorbimento della radiazione solare. Come si è messo in evidenza esaminando le valutazioni dei termini di densità di flusso mostrate in Tav. I B, il bilancio di energia del sistema Terra-atmosfera deve tener conto anche dei termini di flusso di calore latente e sensibile dalla superficie terrestre all'atmosfera. Le distribuzioni orizzontali e verticali delle nubi di vario tipo e delle concentrazioni del vapore acqueo e dei gas-serra variano rapidamente da un giorno all'altro o nel giro di pochi giorni, essendo questi parametri strettamente connessi con l'evolvere della situazione meteorologica in atto nelle diverse regioni del pianeta e con il ciclo giornaliero della radiazione solare. Per effetto di questa variabilità, le quantità di radiazione solare che sono riflesse all'indietro o assorbite dall'atmosfera o trasformate in calore ceduto al suolo e agli oceani variano largamente da un luogo all'altro e da un giorno all'altro, pur seguendo un'evoluzione stagionale abbastanza regolare in funzione della latitudine. In questi processi di trasporto di calore dalle regioni equatoriali alle regioni di alta latitudine, il vapore acqueo svolge un ruolo essenziale, contribuendo allo stesso tempo a modulare la distribuzione latitudinale dell'effetto serra.

Dunque, questi forti squilibri tra energia entrante e uscente possono generarsi sia alla superficie degli oceani sia in atmosfera, mettendo in movimento complessi meccanismi di trasporto di calore su vasta scala, i quali danno vita al composito quadro della circolazione oceanica e a quello assai complesso della circolazione atmosferica, entrambi tendenti a ridistribuire in maniera uniforme gli eccessi di energia delle aree subtropicali e, quindi, a compensare le carenze di energia tipiche delle aree di latitudine più elevata.

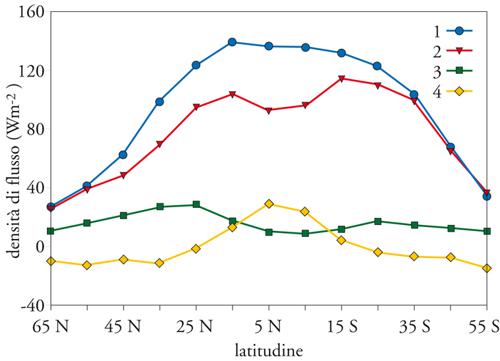
Alla luce di queste considerazioni, appare opportuno considerare in che modo il bilancio netto B_s di radiazione alla superficie varia con la latitudine e come variano i corrispondenti termini di flusso C di calore latente e flusso P di calore sensibile, tenendo conto anche dei processi di trasporto di calore legati alla circolazione oceanica superficiale e del fatto che i processi di scambio di radiazione e di calore possono variare anche in funzione della latitudine e del rapporto tra aree continentali e oceaniche. Alle alte latitudini, il bilancio B_s non varia di molto passando dalle aree oceaniche a quelle continentali, mentre alle latitudini intertropicali, tale parametro presenta valori notevolmente più elevati sugli oceani che non sui continenti, mentre il flusso C, legato all'evaporazione, prevale sopra gli oceani e il flusso P di calore sensibile è maggiore nelle aree continentali.

fig. 8

Come si può vedere in fig. 8, il flusso netto B_s di radiazione alla superficie cresce al diminuire della latitudine, da valori di 25÷35 Wm⁻² a 60° N e 60° S fino a valori di più di 130 Wm⁻² alle latitudini intertropicali. Invece, il flusso C presenta i valori più elevati nella fascia latitudinale compresa tra 30° N e 40° S, entro la quale l'effetto delle aree oceaniche è maggiormente pronunciato e si abbassa avvicinandosi alle latitudini più elevate, presentando valori confrontabili con quelli di B_s. La densità di flusso P assume, invece, i valori più elevati alle latitudini da 20° a 50° in entrambi gli emisferi, grazie all'effetto delle aree continentali. La fig. 8 mostra, dunque, che la fascia compresa tra le latitudini di 30° N e 40° S riceve il contributo predominante di calore latente. D'altra parte, l'andamento del flusso orizzontale D di calore trasportato dalla circolazione oceanica indica in modo evidente che le correnti oceaniche prelevano il calore dalle aree comprese tra 20° N e 20° S e lo trasportano verso le latitudini più elevate.

Le variazioni dei diversi termini del bilancio di radiazione e di calore producono sostanziali differenze nel bilancio locale di energia, da una regione all'altra. Nel sistema Terra-atmosfera si formano conseguentemente delle aree relativamente calde e delle aree relativamente fredde, la cui distribuzione è influenzata dalla presenza di oceani e continenti e muta nel tempo sia per intensità sia per posizione. La circolazione oceanica presenta configurazioni più complesse di quelle della circolazione atmosferica. Generalmente, dalle zone calde delle basse latitudini alle zone fredde delle alte latitudini, si muovono intense correnti negli oceani che sono regolate da forze di superficie, originate in gran parte da variazioni di densità dell'acqua negli strati superficiali (dovute a evaporazione più o meno intensa) e in misura minore dalle interazioni tra i moti atmosferici e l'idrosfera.

Anche l'atmosfera contribuisce in maniera notevole al trasporto di calore dalle zone equatoriali alle zone polari. Laddove gli squilibri del bilancio di energia contribuiscono a creare nell'atmosfera gradienti termici orizzontali e verticali, s'instaurano regimi di vento che trasportano il calore lungo i gradienti che vanno dalle aree calde a quelle fredde. Il quadro della circolazione atmosferica non è semplice: fino a 35° di latitudine, la circolazione avviene in forma di grandi celle (cellule di Hadley) che collegano l'aria umida e calda, che s'innalza sopra la zona equatoriale, con quella secca e meno calda, che scende verso la superficie terrestre alle latitudini maggiori. L'aria calda, che si solleva nella zona equatoriale (zona intertropicale di convergenza), si raffredda durante la salita, causando precipitazioni molto intense e perdendo gradualmente la sua umidità fino a diventare gradualmente più secca, quando scende fino a raggiungere la superficie terrestre nella fascia subtropicale tra i 10° e i 35° di latitudine, dove si trovano le aree desertiche. Nella fascia compresa all'incirca tra i 35° e i 65° di latitudine, la circolazione atmosferica si sviluppa in linea di massima secondo i paralleli, essendo i moti circolatori governati dalle correnti a getto ad alta quota. Questi moti assumono configurazioni sinuose con la formazione e lo sviluppo di aree cicloniche e anticicloniche, cosicché si assiste al movimento alterno di masse d'aria calda dalle basse alle alte latitudini e di masse d'aria fredda in senso inverso. Anche al di sopra dei 65° di latitudine si forma una circolazione a cella, la quale è peraltro caratterizzata da flussi più moderati di quelli che agiscono alle medie latitudini. In queste regioni, la circolazione atmosferica garantisce il trasporto di calore verso le aree polari, nelle quali i processi di condensazione liberano quantità assai modeste di calore. Questi processi dinamici dell'atmosfera assumono un'importanza fondamentale per il clima delle regioni polari, dato che gli effetti delle correnti marine sono del tutto assenti nella regione antartica, a causa dell'ostacolo costituito dal continente Antartico, e sono molto deboli nella regione polare artica, a causa dell'esteso ostacolo opposto dalla banchisa polare alle correnti marine.

Bibliografia

Anderson 1986: Anderson, Gail P. e altri, AFGL Atmospheric constituent profiles (0-120 km), AFGL-TR-86-0110, AFGL (OPI), Hanscom AFB, MA 01736, 1986.

Anderson 2000: Anderson, Gail P. e altri, MODTRAN4: Radiative transfer modeling for remote sensing, in: Algorithms for multispectral, hyperspectral, and ultraspectral imagery VI, edited by Sylvia S. Shen, Michael R., Descour, Orlando, SPIE, 2000, pp. 176-183.

Foukal, Lean 1990: Foukal, Peter - Lean, Juditta, An empirical model of total solar irradiance variations between 1874 and 1988, "Science", 247, 1990, pp. 556-558.

Fröhlich, Brusa 1981: Fröhlich, Claus - Brusa, R.W., Solar radiation and its variation in time, "Solar physics", 74, 1981, pp. 209-215.

Gueymard 2004: Gueymard, Christian A., The sun's total and spectral irradiance for solar energy applications and solar radiation models, "Solar energy", 76, 2004, pp. 423-453.

Intergovernmental Panel on Climate Change 2001: Climate change 2001. The scientific basis, edited by John T. Houghton e altri, Cambridge, Cambridge University Press, 2001.

Iqbal 1983: Iqbal, Muhammad, An introduction to solar radiation, Toronto-London, Academic Press, 1983, pp. 43-58.

Irvine, Pollack 1968: Irvine, William M. - Pollack, James B., Infrared optical properties of water and ice spheres, "Icarus", 8, 1968, pp. 342-360.

Kiehl, Trenberth 1997: Kiehl, Jeffrey T. - Trenberth, Kevin E., Earth's annual global mean energy budget, "Bulletin of the American Meteorological Society", 78, 1997, pp. 197-208.

Kondratyev 1969: Kondratyev, Kirill Y., Radiation in the atmosphere, New York, Academic Press, 1969.

Neckel, Labs 1984: Neckel, Heinz - Labs, Dietrich, The solar radiation between 3300 and 12500 Å, "Solar physics", 90, 1984, pp. 205-258.

Snyder 1998: Snyder, William C. e altri, Classification-based emissivity for land surface temperature measurement from space, "International journal of remote sensing", 19, 1998, pp. 2753-2774.

Thekaekara, Drummond 1973: Thekaekara, Matthew P. - Drummond, Andrew J., Standard values for the solar constant and its spectral components, "Solar energy", 14, 1973, pp. 109-127.

Tomasi 1990: Tomasi, Claudio, L'ozono nell'atmosfera terrestre, Parte I: Caratteristiche fisiche delle diverse regioni atmosferiche, "La chimica nella scuola", 7-8, 1990, pp. 13-19.

Tomasi 2005: Tomasi, Claudio e altri, Improved algorithm for calculations of Rayleigh-scattering optical depth in standard atmospheres, "Applied optics", 44, 2005, pp. 3320-3341.

Tomasi, Trombetti 1985: Tomasi, Claudio - Trombetti, F., Absorption and emission by minor atmospheric gases in the radiation balance of the Earth, "La rivista del nuovo cimento", 8/2, 1985 (numero monografico).

Tavola I

Trasporto della radiazione solare nel sistema superficie-atmosfera

Una rappresentazione schematica dei termini che definiscono il bilancio globale di radiazione B è mostrata nelle figg. A e B (i valori numerici sono in Wm2, basata sulle valutazioni di Kiehl e Trenberth. La fig. A descrive i processi d’interazione tra la radiazione solare e il sistema superficie-atmosfera, presentando le stime medie globali annue dei termini di densità di flusso della radiazione solare e definendo, quindi, le frazioni di radiazione che sono assorbite dalla

superficie e dall’atmosfera e la frazione riflessa verso lo spazio. La fig. B mostra i processi di emissione e assorbimento di radiazione a onda lunga da parte della superficie e dell’atmosfera, fornendo le stime medie globali annue dei termini di densità di flusso della radianza a onda lunga, completando la descrizione dei processi che regolano il bilancio termico del sistema superficie-atmosfera con quelli di scambio di calore tra la superficie terrestre e l’atmosfera. Le valutazioni

dei vari termini in cui si ripartiscono il flusso incidente della radiazione solare e quello uscente della radiazione termica mostrano che il bilancio di radiazione alla superficie terrestre è positivo e quello dell’atmosfera è negativo. Ma grazie al processo di trasporto di energia legato all’evaporazione e alla condensazione del vapore acqueo durante la formazione delle nubi, e a quello del trasporto di calore sensibile legato ai processi di flusso turbolento che coinvolgono lo strato limite dell’atmosfera, i bilanci Bs e Ba di radiazione [6] sono compensati in misura tale da riportare in equilibrio i bilanci di energia alla superficie e in atmosfera.