Transizioni di fase e punti critici

Transizioni di fase e punti critici

Le transizioni di fase sono fenomeni molto familiari: un corpo può passare da uno stato d'aggregazione a un altro (fase) al variare dei parametri, come la temperatura e la pressione, che ne controllano l'equilibrio con l'ambiente circostante. Tutti i corpi presentano almeno tre fasi (solido, liquido e gas) che coesistono al punto triplo, ma la nozione di fase è stata estesa per includere altri stati che può presentare la materia. Per esempio, un materiale magnetico, in assenza di campo magnetico, può presentare due stati o fasi: magnetizzato, vale a dire con momento magnetico M≠0, oppure smagnetizzato, con M=0; aumentando la temperatura al di sopra di un certo valore, caratteristico del materiale, si passa da una fase all'altra. Alcuni metalli cessano di esercitare una qualsiasi resistenza al passaggio della corrente elettrica e diventano superconduttori se sono sufficientemente raffreddati. Analogamente l'elio presenta due fasi fluide: in una si comporta come un fluido normale, nell'altra è un superfluido.

La comprensione di questi fenomeni, quando si cerca di analizzare il processo a livello atomico, ha impegnato i fisici per un periodo molto lungo: la teoria oggi universalmente accettata è stata proposta solamente nell'ultimo quarto del XX secolo. Per capire le difficoltà che si devono affrontare cerchiamo di immaginare che cosa succede alle singole molecole che formano l'acqua, quando la temperatura si abbassa sotto 0 °C. Nella fase liquida le molecole dell'acqua si muovono in maniera completamente disordinata: al contrario, nel ghiaccio le molecole sono ordinate in cristalli, vale a dire in configurazioni fisse che si ripetono regolarmente nello spazio. Perfino un piccolo cristallo di alcuni micron consiste di svariati miliardi di molecole ben ordinate. La transizione liquido-vapore presenta altre caratteristiche microscopiche che sono meno familiari. Alla temperatura di ebollizione, le molecole dell'acqua passano in una fase di vapore, disordinata come il liquido, ma molto meno densa. Se conteniamo il vapore in un tubo molto resistente e aumentiamo la pressione, mantenendo la temperatura costante, si può constatare che il liquido si riforma e appare un menisco che separa le due fasi. Tuttavia, se l'esperimento è effettuato sopra la temperatura critica, pari per l'acqua a 374 °C, non succede niente e il menisco non appare nemmeno alle pressioni più elevate.

Il ferromagnetismo è un altro esempio di transizione di fase che possiede un punto critico, come scoperto da Pierre Curie nel 1890. Un campione di ferro è normalmente attratto da un magnete, ma se si trova al di sopra di 770 °C (il punto di Curie del ferro) perde la sua magnetizzazione. Il ferromagnetismo è una manifestazione macroscopica di un ordine che, a livello atomico, induce gli spin (il momento angolare intrinseco responsabile del momento magnetico dell'elettrone) degli elettroni, appartenenti a una regione chiamata dominio magnetico, ad allinearsi e puntare tutti nella stessa direzione. Queste transizioni di fase sono la manifestazione del comportamento collettivo di un gran numero di costituenti correlati. Ci si può render conto qualitativamente del meccanismo che ne è alla base analizzando il fenomeno della transizione ordine-disordine, che avviene attorno al punto di Curie. Sopra la temperatura di Curie gli spin sono puntati in ogni possibile direzione e la somma su tutto il campione di questi vettori è in media nulla. Il sistema è contemporaneamente disordinato e simmetrico: non presenta direzioni privilegiate. Applicando al campione un piccolo campo magnetico, un maggior numero di spin si orienterà nel verso del campo piuttosto che nel verso opposto; il sistema presenta allora una magnetizzazione che scompare quando il campo magnetico si annulla. Il corrispondente stato della materia è detto paramagnetico. Sotto il punto di Curie appare una magnetizzazione spontanea in assenza di un qualsiasi campo applicato. Il campione sceglie una direzione preferita, perdendo l'isotropia caratteristica della fase ad alta temperatura. In questa fase ferromagnetica il campione è ordinato e la simmetria della fase paramagnetica si è rotta spontaneamente abbassando la temperatura. La magnetizzazione spontanea è il parametro d'ordine caratteristico di questa transizione di fase.

La vicinanza della temperatura critica è segnata da forti fluttuazioni termodinamiche della magnetizzazione. Sebbene l'interazione quantistica tra gli spin abbia un corto raggio di azione, dell'ordine della distanza interatomica, vicino al punto di Curie le correlazioni tra gli spin appaiono fino a una distanza (detta lunghezza di correlazione) che può essere migliaia di volte più grande della distanza interatomica.

I problemi posti alla meccanica statistica dalla descrizione delle transizioni di fase

Alla fine del XIX sec. i principî della meccanica statistica erano stati ben stabiliti; un ruolo molto importante avevano rivestito i lavori di Ludwig Boltzmann a Vienna e di Josiah W. Gibbs a Yale. Per la prima volta era possibile connettere le proprietà macroscopiche della materia, come la compressibilità e l'equazione di stato, ai suoi costituenti microscopici. In particolare, Boltzmann aveva connesso il concetto macroscopico, apparentemente misterioso, di entropia al numero di stati microscopici dell'insieme degli atomi per un dato valore dell'energia totale. L'entropia appariva quindi come una misura quantitativa dell'ordine. Il comportamento qualitativo di un sistema può essere spesso compreso se si considera l'energia libera, una quantità termodinamica definita come E−TS, vale a dire l'energia E meno il prodotto tra l'entropia S e la temperatura termodinamica T. All'equilibrio, un sistema isotermo si trova nella configurazione macroscopica di minima energia libera. Esiste quindi una competizione tra l'energia (che richiede ordine) e l'entropia, competizione che è arbitrata dalla temperatura.

A bassa temperatura, l'energia è il termine dominante nell'espressione dell'energia libera e il sistema si ordina; al contrario, ad alta temperatura l'entropia è il termine dominante e la minimizzazione dell'energia libera si realizza portando l'entropia a un valore elevato e, conseguentemente, il sistema in uno stato disordinato. Pertanto, a temperature molto basse l'energia è la minore possibile: gli atomi si dispongono in una configurazione che permette loro di beneficiare al massimo delle reciproche interazioni per abbassare la loro energia. Questa condizione implica che l'insieme degli atomi può assumere soltanto un numero molto ristretto di configurazioni, quindi la loro entropia è piccola e il sistema è ben ordinato. A temperature elevate, diventa più vantaggioso per il sistema stare in configurazioni di energia più alta, meno ordinate, considerato che il numero degli atomi, ovvero l'entropia, supera il loro costo energetico.

Sebbene questo comportamento qualitativo fosse ben compreso, anche dopo l'introduzione della meccanica statistica, rimaneva aperto il problema delle transizioni di fase, ossia del cambiamento discontinuo degli stati della materia. Infatti, l'analisi precedente sarebbe stata compatibile con un graduale cambiamento da uno stato ordinato a bassa temperatura a uno stato disordinato ad alta temperatura. Negli anni Trenta del Novecento, alcuni fisici misero in discussione la possibilità di spiegare i bruschi cambiamenti che accadono durante le transizioni di fase utilizzando la meccanica statistica. Ci si domandava se fosse necessario aggiungere nuove regole per permettere la coesistenza delle fasi e il cambiamento discontinuo da una fase all'altra. In pratica, molto spesso si costruisce una teoria per la fase A (supponiamo il gas) e un'altra per la fase B (diciamo il liquido); solo successivamente si passa a esprimere le condizioni per la loro coesistenza. Non era quindi chiaro se esistesse una descrizione unica delle interazioni tra le molecole che poteva rendere conto simultaneamente sia della fase A sia della B. Il fenomeno delle simmetrie rotte spontaneamente lasciava molto perplessi: come è possibile che soltanto a basse temperature la simmetria di quello che si osserva sia minore della simmetria delle interazioni? Inoltre, l'analisi teorica era confusa dalla dimostrazione (che si può fare facilmente sulla base dei principî primi della meccanica statistica) che un'orientazione preferenziale, come in un ferromagnete, non può mai accadere in un sistema composto da un numero finito di costituenti, come avviene sempre in natura. In altre parole, un uso troppo ingenuo della teoria portava alla conclusione che non esistono transizioni di fase. In realtà quest'argomento non era conclusivo, in quanto il numero di costituenti di qualunque pezzo di materia, anche di uno molto piccolo, è enorme (la più piccola goccia d'acqua consiste di milioni di miliardi di molecole). Al di sotto della temperatura critica, una qualsiasi asimmetria, non importa quanto piccola, ha un effetto macroscopico. Quindi, in condizioni normali, la finitezza del numero di costituenti è irrilevante. Questo è il motivo per il quale si assiste a improvvisi e bruschi cambiamenti, quando si verificano transizioni di fase.

La comprensione teorica migliorò durante il periodo della Seconda guerra mondiale, per effetto di due successivi contributi estremamente importanti. Per primo Rudolf E. Peierls, un rifugiato tedesco nel Regno Unito, dimostrò nel 1941 che in un'ampia classe di materiali magnetici la magnetizzazione spontanea, indice di una rottura spontanea di una simmetria, doveva necessariamente apparire a temperature sufficientemente basse. In seguito Lars Onsager, un norvegese che lavorava negli Stati Uniti, calcolò esattamente le proprietà statistiche a tutte le temperature, mettendo in evidenza l'esistenza di una transizione di fase ferromagnetica, del più semplice modello microscopico di spin interagenti, il cosiddetto modello di Ising, che era stato introdotto da Ernest Ising nella sua tesi di dottorato. Nonostante la grande semplicità del modello, la soluzione richiese un'analisi matematica molto complessa, che Onsager riuscì a portare fino in fondo solamente nel caso del modello a due dimensioni. Dopo più di mezzo secolo di ricerche, nessuno è ancora riuscito a risolvere il modello tridimensionale, che ovviamente è più interessante dal punto di vista fisico. Tuttavia la soluzione di Onsager permise un passo avanti storico, poiché confermò che i principî primi della meccanica statistica, senza ulteriori aggiunte o assunzioni, contenevano la possibile esistenza di una transizione di fase.

Il periodo classico

Uno degli esperimenti effettuati da Pierre Curie sul magnetismo, nel 1895, consisteva nello studio della reazione del sistema a un campo magnetico esterno. Nella fase disordinata ad alta temperatura, il sistema sviluppa una piccola magnetizzazione che si annulla quando il campo magnetico applicato viene portato a zero. Il rapporto tra la magnetizzazione e il campo esterno, ovvero la suscettività magnetica, è piccolo ad alte temperature, ma diventa sempre più grande quando, diminuendo la temperatura, ci si avvicina al punto di Curie. Paul Langevin, che aveva lavorato con Curie, spiegò il basso valore della suscettività ad alte temperature usando un modello di spin accoppiati con il campo magnetico esterno, dove venivano trascurate le loro reciproche interazioni. Questo semplice modello è del tutto incapace di spiegare l'esistenza a basse temperature di uno stato ordinato ferromagnetico, la cui natura cooperativa richiede necessariamente la presenza di interazioni tra i vari spin.

La teoria del campo medio, sviluppata nel 1907 da Pierre Weiss, ha facilitato notevolmente la comprensione del ferromagnetismo. Weiss assumeva che ogni spin fosse soggetto sia al campo magnetico esterno, sia a un ulteriore campo molecolare creato dagli atomi vicini. L'intensità di questo campo addizionale aumenta con la magnetizzazione. Si arriva così a una descrizione autoconsistente dove la magnetizzazione del sistema, inizialmente sconosciuta, è creata dall'effetto combinato del campo esterno e del campo molecolare, quest'ultimo proporzionale alla magnetizzazione. All'epoca la natura del campo molecolare era del tutto sconosciuta e soltanto 25 anni dopo Werner Heisenberg capì che aveva origine da un effetto quantistico. Questo nuovo modello era in accordo con la legge di Curie e con il modello di Langevin ad alte temperature, ma con un'importante differenza: prediceva l'esistenza di una transizione di fase alla temperatura di Curie, di una magnetizzazione spontanea al di sotto di questa temperatura e di una divergenza esplicita di certe quantità vicino al punto critico. Per esempio, la suscettività magnetica era inversamente proporzionale alla differenza della temperatura dalla temperatura di Curie, e quindi poteva essere arbitrariamente grande vicino al punto critico; inoltre la magnetizzazione spontanea nella fase ferromagnetica, dove la temperatura T è più bassa di T_c, svanisce come (T_c−T)^1/2.

Già nel 1873, in Olanda, Johannes D. van der Waals aveva proposto una teoria fenomenologica per la transizione liquido-gas. Essa aveva ricevuto immediatamente una grande attenzione in quanto, in accordo con la scoperta di Thomas Andrews, prediceva una sola fase fluida al di sopra della temperatura critica e una transizione liquido-gas al di sotto. Alcuni dettagli del comportamento in vicinanza del punto critico trovati da Weiss per i magneti erano simili a quelli rilevati da van der Waals per i fluidi. Per esempio, la compressibilità del fluido aumentava in prossimità del punto critico esattamente come la suscettività magnetica della legge di Curie-Weiss. All'epoca queste teorie erano in accordo ragionevole con gli esperimenti e la loro validità non era messa in discussione. Un approccio sistematico, che si rivelò molto importante, fu proposto successivamente dal fisico teorico russo Lev Davidovič Landau, che nel 1936 formulò una teoria generale delle transizioni di fase e del comportamento critico. Questa teoria macroscopica era di natura termodinamica e non si proponeva, al contrario dei lavori di Langevin e Weiss, di connettere le proprietà osservate sperimentalmente con l'interazione dei gradi di libertà microscopici. Landau introdusse il concetto di parametro d'ordine, delle proprietà di simmetria della fase disordinata, della rottura spontanea della simmetria nella fase ordinata. La teoria puntava a descrivere tutte le possibili transizioni di fase: la sua semplicità e la sua grande applicabilità la resero uno degli strumenti più usati per cercare di capire i cambiamenti di stato della materia. Il comportamento quantitativo del sistema era in accordo con le precedenti teorie di van der Waals e di Weiss.

Le difficoltà della teoria classica: leggi di scala e universalità

fig. 1

fig. 2

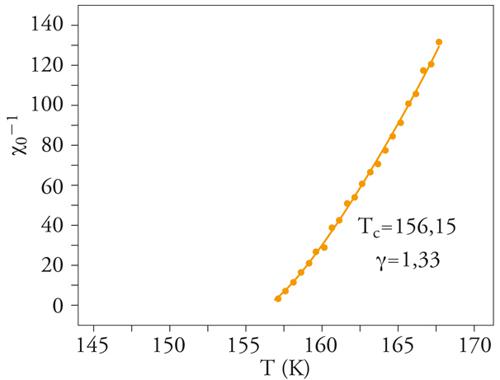
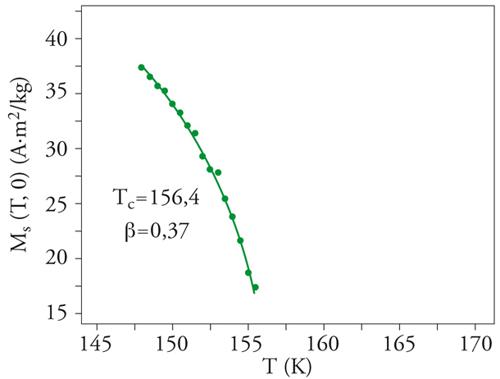
Negli anni Sessanta diventarono disponibili nuove tecniche sperimentali, in particolare la diffusione della luce del laser, applicata allo studio dei fluidi o di miscele binarie che si separano, lo scattering di neutroni e la spettroscopia RMN (Risonanza magnetica nucleare), usate nell'analisi dei fenomeni magnetici. I risultati ottenuti con queste nuove tecniche erano estremamente interessanti, ma contraddicevano le idee teoriche prevalenti all'epoca. Per esempio, la suscettività di un magnete non era semplicemente proporzionale alla differenza di temperatura (T−T_c), ma aumentava un poco più velocemente (fig. 1). Questa crescita poteva essere caratterizzata da una legge di potenza con un esponente detto esponente critico; per esempio, la suscettività magnetica di un ferromagnete diverge come 1/(T−T_c)^γ quando la temperatura viene abbassata fino al punto di Curie; vicino al punto critico liquido-gas, la lunghezza di correlazione ξ diverge come 1/(T−T_c)^ν (in questo caso T_c è la temperatura del punto critico), producendo l'opalescenza critica, che è il segno dei grandi domini correlati di grandezza paragonabile a quella della lunghezza d'onda della luce e quindi costituiti da miliardi di molecole; la magnetizzazione spontanea nella fase ferromagnetica svanisce come (T_c−T)^β (fig. 2), e così via.

Nella teoria classica i valori attribuiti a questi esponenti critici erano semplici e di generale applicazione. Essa prediceva che per tutte le transizioni di fase si dovesse avere γ=1, ν=1/2, β=1/2. Era noto che tali valori erano in contraddizione con i risultati ottenuti da Onsager nella sua soluzione del modello di Ising bidimensionale (che erano γ=7/4, ν=1, β=1/8). Tuttavia, la natura bidimensionale del modello e alcune caratteristiche non realistiche, senza le quali il modello non si sarebbe potuto risolvere, facevano probabilmente pensare che il disaccordo con un modello così lontano dalla realtà fisica non implicasse necessariamente che la teoria classica dovesse essere modificata nella sua applicazione a sistemi fisici realistici. I problemi apparvero in tutta la loro evidenza quando nuovi esperimenti, molto precisi, mostrarono che, in vicinanza del punto critico, i risultati sperimentali erano invariabilmente in disaccordo con la teoria classica. Inoltre, la loro analisi rivelò caratteristiche sorprendenti, che furono analizzate negli anni Sessanta: le leggi di scala e l'universalità.

Le leggi di scala si manifestano in modi differenti. Supponiamo, per esempio, di misurare la magnetizzazione M come funzione del campo magnetico H e della temperatura T, sia sotto sia sopra il punto di Curie. Per ogni valore di T possiamo tracciare il diagramma della magnetizzazione come funzione di H, e in questo modo rappresentare i dati come un insieme di curve, ognuna diversa dall'altra. Tuttavia, se per realizzare i diagrammi vengono scelte delle variabili opportune (per es., M/(T−T_c)^β), in funzione di H/(T−T_c)^β+γ, tutti i dati nella regione al di sopra della temperatura in prossimità del punto critico si dispongono su una sola curva, quasi come se vicino alla temperatura critica il sistema fosse invariante rispetto a un cambiamento simultaneo della scala della temperatura, misurata come distanza dal punto critico, del campo magnetico e della magnetizzazione. Nello stesso modo, i risultati delle misure delle correlazioni spaziali mediante esperimenti di diffusione possono essere rappresentati come un insieme di curve: la correlazione come funzione della distanza tra due punti al variare della temperatura. La funzione di correlazione decade esponenzialmente con la distanza r mediante una lunghezza di correlazione ξ che diverge al punto critico. Se si costruisce il diagramma delle varie curve che rappresentano la correlazione come funzione della variabile ridotta r/ξ, tutte queste curve, scegliendo in modo opportuno la scala verticale, si dispongono su un'unica curva, nonostante ξ vari enormemente con la temperatura.

Queste leggi di scala implicano, inoltre, che gli esponenti critici ‒ finora ne abbiamo introdotti solo tre, ma ce ne sono molti di più che caratterizzano altre proprietà fisiche, come il calore specifico ‒ non siano indipendenti. Si trova infatti che tutti possono essere espressi come funzione di due esponenti critici. Per esempio, tanto gli esperimenti quanto i risultati di modelli esattamente risolubili, sono tutti compatibili con la relazione 2β+γ=dν, dove d è la dimensione dello spazio; per via sperimentale si ha ovviamente d=3, tranne che per campioni estremamente sottili; questa relazione è interessante anche per d diverso da 3, in quanto è soddisfatta sia dai risultati di Onsager per il modello di Ising bidimensionale, sia dai risultati classici di Landau in quattro dimensioni per ragioni che saranno discusse in seguito. Il quadro che emergeva da questi risultati empirici sulle leggi di scala era di un sistema che rimaneva simile a sé stesso quando veniva osservato su svariate scale di lunghezza, dalle distanze interatomiche fino alla lunghezza di correlazione. Era come se ingrandendo il sistema dalla scala molecolare fino alla lunghezza di correlazione si vedessero via via immagini differenti ma simili l'una all'altra, un fenomeno che successivamente verrà molto studiato; sistemi con queste proprietà furono chiamati frattali.

Una volta dimostrato che la teoria classica era incompatibile con gli esperimenti, l'ipotesi più naturale era di supporre che ogni sistema possedesse il suo proprio insieme di esponenti critici, le sue curve riscalate, e così via. Non era così: furono studiate centinaia, forse migliaia di punti critici liquido-gas e la temperatura critica variava su una scala enorme, dai 268 °C dell'elio ai 31 °C per l'anidride carbonica. Tuttavia, si rilevava che gli esponenti critici erano gli stessi per tutte le transizioni prese in considerazione (γ, per es., era vicino a 1,24 e ν vicino a 0,63); nello stesso modo, tutte le curve riscalate, nelle unità ridotte e precedentemente introdotte, erano identiche per tutti i differenti campioni. Questo dimostrava che le proprietà riportate vicino al punto critico erano universali, vale a dire indipendenti dal sistema considerato. I numerosi studi sperimentali condotti in quel periodo trovarono infatti che, non solo le proprietà critiche di tutti i fluidi erano identiche, ma erano anche identiche in tutti i sistemi dove la transizione era descritta da un parametro d'ordine scalare, cioè non vettoriale: fluidi, miscele binarie, magneti la cui magnetizzazione spontanea è allineata con un'asse di simmetria del cristallo, ecc. Tuttavia, in altri sistemi, come nella transizione dall'elio normale all'elio superfluido o nei magneti in cui la magnetizzazione si orienta in un piano privilegiato, il parametro d'ordine era un vettore bidimensionale e le proprietà critiche cadevano in un'altra classe. Ci si rese conto allora che esistevano classi d'universalità: per determinare a quale classe appartenesse un particolare punto critico era sufficiente conoscere la natura delle simmetrie che governano le interazioni tra i costituenti. Tali osservazioni lasciavano i fisici sconcertati e incuriositi: per un lungo periodo non s'intravide che tipo di descrizione potesse rendere conto di risultati che erano indipendenti dai dettagli della dinamica.

Capire il motivo per cui la teoria classica non funzionava non fu difficile. La teoria di Landau era basata su considerazioni puramente termodinamiche. La teoria del campo molecolare, che prediceva gli stessi risultati classici, assumeva che in un dato istante in ogni punto del campione tutti i costituenti microscopici subissero influenze dei vicini che non fluttuavano con il tempo. In questo modo si trascuravano le fluttuazioni sia spaziali sia temporali, mentre gli esperimenti rivelavano l'esistenza di forti fluttuazioni su tutte le scale. Le lacune della teoria erano facili da identificare, ma i rimedi non sembravano funzionare. Se si cercava di correggere gli svantaggi della teoria del campo medio omogeneo e di tener conto delle fluttuazioni, che in prima approssimazione si supponevano piccole, si notava che le correzioni alla teoria classica erano troppo forti e addirittura divergevano, quando ci si avvicinava al punto critico. Se si assumeva come punto di partenza la teoria di campo medio, ci si trovava immediatamente in una regione di grandi fluttuazioni che interagivano fortemente, dove tutti gli schemi teorici noti fallivano miseramente. Alla fine degli anni Sessanta tale problema era considerato come uno tra i più importanti di tutta la fisica. La soluzione stava per arrivare, ma da un'area completamente inattesa della fisica teorica: la strada fu aperta da una nuova e accurata analisi del gruppo di rinormalizzazione, una tecnica molto formale della teoria dei campi quantistici.

Il nuovo approccio: l'analisi basata sul gruppo di rinormalizzazione

Questo nuovo modo di analizzare le proprietà di un sistema composto di un grande numero di costituenti fu introdotto nei primi anni Settanta da Kenneth Wilson, un teorico che lavorava sulle interazioni tra le particelle elementari (nel 1982 gli fu conferito il premio Nobel per la fisica per la teoria dei fenomeni critici). Allo scopo di sviluppare una nuova comprensione della natura delle interazioni tra particelle elementari, Wilson aveva riformulato una vecchia tecnica formale, chiamata gruppo di rinormalizzazione, e aveva dimostrato la sua applicabilità ai fenomeni critici, arrivando a fornire una spiegazione, oggi universalmente accettata, delle loro misteriose proprietà di scala e di universalità. Come spesso accade, esistono precursori delle nuove idee. Un passo in avanti molto significativo era stato compiuto nel 1967 da Leo Kadanoff, che aveva introdotto molte delle idee che furono alla base degli sviluppi successivi. Inoltre, l'uso di tecniche simili a quelle delle particelle elementari era stato introdotto da Vladimir N. Gribov, Alexander Migdal e Alexander M. Polyakov; la possibilità di utilizzare il gruppo di rinormalizzazione era stata suggerita da Carlo di Castro e Giovanni Jona Lasinio; tuttavia, fu solo con il lavoro di Wilson che queste varie idee furono unificate in una teoria coerente, capace di fare predizioni quantitative, anche estremamente accurate.

Per illustrare le idee alla base del gruppo di rinormalizzazione prendiamo in esame un reticolo di spin, dove soltanto gli spin vicini interagiscono, vale a dire essenzialmente il modello di Ising. Come risultato di queste interazioni, l'energia di due spin vicini è più bassa quando sono paralleli rispetto a quando sono antiparalleli. Risulta conveniente introdurre un parametro J, definito come il rapporto tra questo guadagno in energia e la temperatura: tale parametro, se espresso in unità opportune, è un numero puro. Vicino al punto critico la lunghezza di correlazione ξ(J) è grande se paragonata al passo reticolare (bisogna ricordare che la lunghezza di correlazione varia al variare della temperatura e quindi di J). Consideriamo un piccolo blocco di siti vicini del reticolo. Se gli spin dentro questo blocco fossero orientati in maniera completamente casuale, la lunghezza di correlazione sarebbe uguale a pochi passi reticolari. Al contrario, quando la lunghezza di correlazione è grande, gli spin del blocco sono fortemente correlati. Pertanto, si può ragionevolmente supporre che, nella regione vicino al punto critico, dove la lunghezza di correlazione è enorme, se dividiamo l'intero reticolo in blocchi di lato b, una descrizione adeguata della configurazione degli spin si può ottenere rappresentando un blocco di spin come un solo spin uguale alla media degli spin che lo costituiscono.

fig. 4

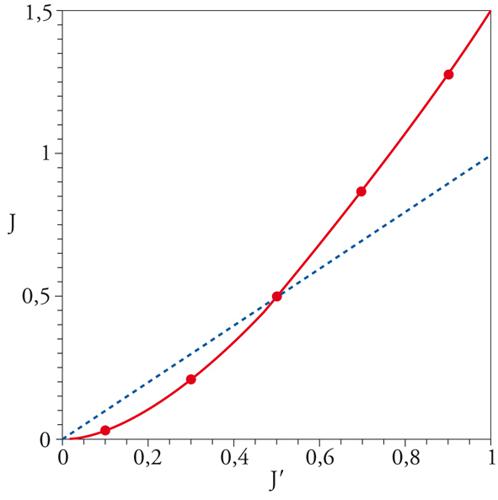
In questo modo ci siamo costruiti un nuovo modello dove gli spin del blocco interagiscono tra di loro (un argomento più dettagliato mostra che l'energia dello spin che rappresenta un blocco dipende essenzialmente dagli spin che rappresentano i blocchi vicini). Il passo reticolare del nuovo reticolo è più grande di un fattore b, che è ovviamente maggiore di 1 (per es., se in tre dimensioni il reticolo è cubico e un blocco è costituito da un cubo elementare con otto spin, b è uguale a 2). In prima approssimazione, solo i blocchi di spin vicini interagiscono e la forza di questa interazione è caratterizzata da un nuovo parametro J′ che dipende da J e quantifica il guadagno in energia quando gli spin che rappresentano due blocchi vicini sono paralleli invece che antiparalleli. Possiamo quindi scrivere J′=f(J), dove f è una funzione appropriata che può essere stimata mediante delle approssimazioni semplici (fig. 4). La nuova lunghezza di correlazione degli spin che rappresentano i blocchi è la stessa degli spin originari, ma se misurata in unità del nuovo reticolo è divisa per b. Si arriva quindi alla relazione tra le due lunghezze di correlazione: ξ(J′)=ξ(J)/b. Alla temperatura critica del sistema iniziale, chiamiamo J_c la quantità tale che la lunghezza di correlazione va ainfinito. Quindi, a questa temperatura, il lato destro della precedente relazione è infinito: di conseguenza anche il lato sinistro è infinito e J′ risulta essere uguale a J_c. Possiamo anche affermare che J_c è il punto fisso di questa trasformazione, vale a dire una quantità che è lasciata invariante dalla trasformazione. Inoltre, una semplice analisi matematica mostra che l'esponente ν, che controlla la divergenza della lunghezza di correlazione vicino al punto critico, può ottenersi mediante una linearizzazione di questa trasformazione ed esprimersi in termini della derivata di f(J) calcolata in J_c.

Tale presentazione è molto semplificata e non tiene conto delle interazioni tra spin che rappresentano blocchi non contigui e che appaiono se viene fatta un'analisi che considera in maniera appropriata le fluttuazioni degli spin nei vari blocchi. Se si procede come indicato, si ottengono dei risultati qualitativamente corretti, ma non sufficientemente precisi per fare un confronto quantitativo con gli esperimenti. Tuttavia, essa introduce molte delle idee che contribuiscono con successo all'analisi finale: (a) la dinamica del sistema può essere descritta su scale differenti e la descrizione su una scala più grande può essere ottenuta a partire da quella su una scala più piccola, a patto di utilizzare i nuovi parametri che caratterizzano l'interazione alla nuova scala; (b) il punto critico è un punto fisso della trasformazione che connette i parametri a una data scala con i parametri a una scala più piccola; (c) gli esponenti critici e le funzioni di scala sono ottenuti linearizzando questa trasformazione vicino al punto fisso. In questo quadro gli esponenti critici non dipendono tanto dalla forma originaria dell'interazione sulla scala atomica, quanto dalle proprietà della trasformazione vicino al suo punto fisso. Questo risultato è ilprimo passo per comprendere l'universalità, ossia l'indipendenza del comportamento critico dallo specifico sistema che si sta considerando.

In linea di principio l'analisi di Wilson non trascura nessun grado di libertà e affronta il sistema reale in tutta la sua complessità. Consideriamo una configurazione, ovvero una distribuzione spaziale degli spin: essa è caratterizzata dalle correlazioni a diverse lunghezze, dalla più piccola, la spaziatura del reticolo, a quelle più lunghe, dell'ordine della lunghezza di correlazione. Secondo i principî della meccanica statistica, le proprietà all'equilibrio possono calcolarsi facendo una somma, opportunamente pesata, su tutte le possibili diverse configurazioni degli spin. Tuttavia, in generale non è noto come fare in pratica questa somma enorme: un minuscolo sistema di un migliaio di spin necessita di una somma su un numero astronomico di configurazioni ‒ un numero di 300 cifre ‒ e il più piccolo sistema fisico contiene miliardi di costituenti. Il metodo di Wilson consiste nell'effettuare all'inizio la somma sui gradi di libertà del sistema che si riferiscono alla lunghezza d'onda più corta. Dopo aver eseguito questa somma parziale, rimaniamo con un nuovo sistema in cui compaiono solo i gradi di libertà sulle scale più grandi. Questo sistema è caratterizzato da una nuova interazione: il cambiamento nella forma dell'interazione viene dalla somma sui gradi di libertà sulla scala più piccola, che erano accoppiati a quelli su scala più grande e quindi modificano la forma della loro interazione originaria. Utilizzando questa tecnica si ottiene nuovamente il risultato che sta alla base della formulazione moderna del gruppo di rinormalizzazione: un cambiamento nella scala della lunghezza induce un cambiamento dei parametri dell'interazione che descrive il sistema a quella scala.

Possiamo visualizzare tale fenomeno introducendo un flusso nello spazio dei parametri dell'interazione, che porta i parametri dell'interazione stessi su scala più piccola in quelli su scala più grande. Se questa operazione è ripetuta in maniera iterativa, a partire dalla scala microscopica fino ad arrivare alla scala fisica più grande, quando modifichiamo il valore di un parametro rispetto al suo valore al punto critico emergono due tipi principali di comportamento: (a) i parametri si evolvono, quando la scala diventa sempre più grande, verso il punto fisso; il parametro modificato è quindi irrilevante, in quanto, indipendentemente dal suo valore originario, rimaniamo sempre al punto fisso; (b) i parametri si allontanano dal punto fisso all'aumentare della scala; il parametro è rilevante, in quanto, se non è scelto esattamente al punto fisso, porta il sistema lontano dalla zona di criticità. In pratica, si trova che ci sono solamente pochi parametri che sono rilevanti, ovvero che devono essere scelti con cura per stare al punto critico. Per esempio, in un magnete il campo magnetico deve essere nullo e la temperatura deve essere fissata esattamente al punto di Curie. Ogni altro parametro che può essere usato per descrivere l'interazione tra gli spin è irrilevante, e questo spiega l'universalità osservata sperimentalmente. Nello stesso modo in un fluido, una volta che due parametri connessi alla pressione e alla temperatura sono fissati al punto critico, tutti gli altri sono irrilevanti. Il gruppo di rinormalizzazione spiega perfettamente le proprietà osservate d'invarianza di scala e di universalità. Tuttavia, rimane il problema delicato di usare il gruppo di rinormalizzazione per il calcolo degli esponenti critici e delle varie funzioni universali di scala per le differenti classi di universalità. A tale scopo sono state sviluppate diverse ed elaborate tecniche, basate sul gruppo di rinormalizzazione, utilizzando sia strumenti analitici, sia simulazioni numeriche, e attualmente possiamo affermare che i misteri del comportamento critico sono ben compresi.

Le transizioni di fase in altri contesti

Questi sviluppi della teoria del gruppo di rinormalizzazione hanno avuto un'influenza considerevole su altri problemi, alcuni dei quali apparentemente non collegati. Per esempio, immediatamente dopo i lavori di Wilson, Pierre-Gilles de Gennes intuì che le proprietà geometriche delle soluzioni di polimeri potevano essere comprese utilizzando il gruppo di rinormalizzazione. La distanza tra i due capi di una catena polimerica aumenta con il numero dei monomeri e l'aumento è caratterizzato da un esponente n. Una lunga catena è un oggetto autosimile su distanze grandi se paragonate a quelle di monomeri consecutivi. Anche in questo problema l'esponente n è universale, ovvero indipendente dalla natura esatta dei monomeri e dalle loro mutue interazioni repulsive. C'era una semplice relazione tra n e le dimensioni frattali di questo polimero. Le dimensioni frattali sono una generalizzazione dell'usuale nozione di dimensione dovuta al matematico Felix Haussdorf, la cui presenza ubiqua nel mondo reale è stata enfatizzata da Benoît Mandelbrot. Questa comprensione dell'universalità delle proprietà dei polimeri era basata su una brillante trasposizione delle idee sviluppate per le transizioni di fase.

Lo stesso accade nei modelli per la percolazione: esistono numerosi modelli che descrivono la conducibilità elettrica di una miscela di palline conduttori e isolanti. La geometria dei cammini conduttori presenta di nuovo proprietà universali di autosomiglianza che possono essere comprese in maniera sia qualitativa sia quantitativa mediante il gruppo di rinormalizzazione.

Negli ultimi trent'anni sono stati scoperti molti altri tipi di transizioni di fase con punto critico tra stati diversi della materia e il loro studio si basa su idee simili. Ci sono molte transizioni tra le varie fasi dei cristalli liquidi, ossia le molecole che sono utilizzate per la costruzione degli schermi piatti dei calcolatori e dei televisori. L'ordine nei cristalli liquidi è a metà strada tra quello di un liquido e quello di un solido. Le molecole hanno una forma simile a quella di sigari o aghi. Nella fase nematica, questi aghi sono tutti allineati ed esibiscono un ordine orientazionale, ma i loro centri sono disordinati come le molecole di un liquido. Nella fase smectica le molecole sono organizzate in strati regolari equidistanti gli uni dagli altri come in un solido, ma si muovono come in un liquido all'interno dello stesso strato. Esistono molte transizioni di fase tra queste diverse situazioni che si possono ottenere cambiando la temperatura o la concentrazione; esse sono anche importanti per la comprensione di strutture biologiche come le membrane.

Tuttavia le transizioni di fase non sono presenti soltanto nell'ordinaria materia condensata. L'Universo, la sua dinamica e le strutture su grande scala presenti in esso sono dominate da un certo numero di transizioni di fase.

Il modello cosmologico del big bang, la singolarità iniziale che corrisponde all'origine dello spazio, del tempo e della materia, è descritto ai nostri giorni da una teoria di universo inflazionario che prevede l'esistenza di una transizione di fase, una rottura spontanea di simmetria responsabile dell'apparizione della radiazione e successivamente della materia.

Nei primi microsecondi che seguirono il big bang, le particelle fondamentali che compongono l'attuale materia dei nuclei, i quark legati fra di loro dai gluoni, erano liberi di muoversi, mentre adesso sono confinati permanentemente dentro i neutroni e i protoni. L'Universo è passato quindi da una fase di quark liberi a una fase di quark confinati. Attualmente molti esperimenti studiano collisioni tra ioni estremamente pesanti con lo scopo di produrre nella direzione inversa la transizione di fase che confina permanentemente questi quark: si spera di osservare per pochi cortissimi istanti un plasma di quark, prima che ridiventino confinati a causa del loro immediato raffreddamento.

L'attuale Modello Standard di tutte le interazioni fondamentali tra le particelle elementari, gravità esclusa, cioè le forze elettromagnetiche, deboli e forti, richiede l'esistenza di una nuova specie, ancora da scoprire, di particelle: i bosoni di Higgs. Poco dopo il big bang il campo quantistico associato a questi bosoni dovrebbe attraversare una transizione di fase che è all'origine del corto raggio di azione delle forze deboli, mentre la loro controparte, le forze elettromagnetiche, rimangono con un lungo raggio d'azione.

La storia delle vicissitudini necessarie per arrivare a una comprensione delle transizioni di fase e della natura divergente delle fluttuazioni critiche fa parte ormai del passato. Tuttavia le idee sviluppate stanno ancora influenzando molte aree della fisica e dei sistemi complessi, sistemi eterogenei composti di molti gradi di libertà fortemente correlati. Il gruppo di rinormalizzazione è una teoria estremamente solida che permette di comprendere l'emergenza di comportamenti collettivi e trova quindi applicazioni in un elevato numero di aree della ricerca contemporanea.

Bibliografia

Curie 1908: Curie, Pierre, Oeuvres, Paris, Société Française de Physique, 1908.

Kadanoff 2000: Kadanoff, Leo, Statistical physics: statics, dynamics and renormalization, Singapore, World Scientific, 2000.

Kleman, Lavrentovich 2003: Kleman, Maurice - Lavrentovich, Oleg D., Soft matter physics: an introduction, New York, Springer, 2003.

Landau 1965: Landau, Lev Davidovič, Collected papers, New York, Pergamon, 1965.

Landau, Lifshitz 1969: Landau, Lev D. - Lifshitz, Evgeni M., Statistical physics, Reading (Mass.), Addison-Wesley, 1969.

Ma 1985: Ma, Shang-Keng, Modern theory of critical phenomena, Singapore, World Scientific, 1985.

Onsager 1944: Onsager, Lars, Crystal statistics. I. A two-dimensional model with an order-disorder transition, "Physical review", 65, 1944, pp. 117-149.

Stanley 1987: Stanley, Eugene H., Introduction to phase transitions and critical phenomena, New York, Oxford University Press, 1987.

Weiss 1907: Weiss, Pierre, L'hypothèse du champ moléculaire et la propriété ferromagnétique, "Journal de physique pure et appliquée", 6, 1907, pp. 661-690.

Wilson, Kogut 1974: Wilson, Kenneth G. - Kogut, John, The renormalization group and the epsilon expansion, "Physics reports", C12, 1974, pp. 75-200.

Yeomans 1992: Yeomans, Julia M., Statistical mechanics of phase transitions, Oxford, Clarendon, 1992.