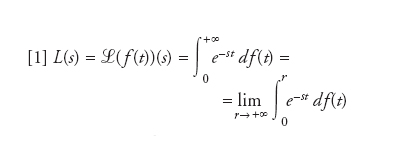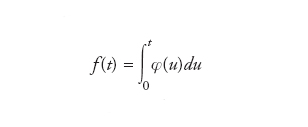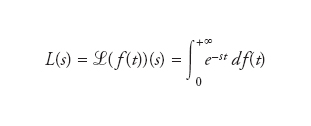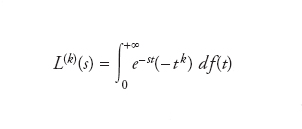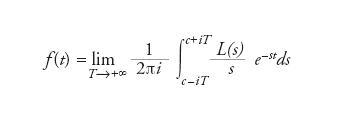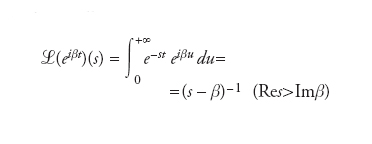trasformata di Laplace
trasformata di Laplace
Nozione introdotta da Pierre-Simon de Laplace nel suo famoso Théorie analitique des probabilités (1812) e da lui utilizzata per risolvere equazioni differenziali e alle differenze finite. Nel secolo scorso è stata utilizzata per giustificare il calcolo operazionale ma più in generale essa è divenuta uno strumento insostituibile nella matematica applicata. Sia f(t):ℝ+→ℂ una funzione a variazione limitata sull’intervallo [0,r] per ogni r positivo. Se
formula
converge per qualche numero complesso s0, allora converge anche per ogni s tale che Res>Res0. L(s) è detta trasformata di Laplace-Stieltjies di f(t). Se invece
[2] formula
è integrabile secondo Lebesgue nell’intervallo [0,r] per ogni r>0, allora
[3] formula
è detta trasformata di Laplace di φ(t). Data la trasformata di Laplace L(s) di f(t), esiste un numero reale σc tale che la massima regione di convergenza del limite in [1] è l’insieme di tutti gli s tali che Res>σc. Se l’integrale non converge mai si scrive allora σc=+∞, se converge ovunque σc=−∞. Il numero σc è detto ascissa di convergenza di L(s) e la linea Res=σc asse di convergenza. Nella regione di convergenza Res>σc, L(s) è una funzione olomorfa e si ha (analogamente al caso della trasformata di Fourier)
[4] formula,
dove L(k)(s) è la derivata k-esima di L(s). Anche la trasformata di Laplace può essere definita per funzioni φ(t): ℝn+→ℂ. Se la funzione f(t) è sufficientemente regolare, essa è unicamente determinata dalla sua trasformata di Laplace L(s) e la formula di inversione è esplicitamente
[5] formula
per t>0. Altre importanti applicazioni della trasformata di Laplace sono nell’ambito della teoria dei semigruppi di operatori e delle distribuzioni. Nel primo caso una generalizzazione della
formula [6]
e della sua inversa fornisce una relazione tra un semigruppo e il suo generatore (teorema di Hille-Yosida), nel secondo permette di caratterizzare le proprietà di regolarità di certe distribuzioni su ℝn a partire da proprietà (quali il supporto) della loro trasformata. Una tecnica, quest’ultima, che si è rivelata fondamentale per es. nella teoria dei campi quantistica, dove i campi stessi sono appunto definiti come distribuzioni con valori nello spazio degli operatori (non-limitati) su uno spazio di Hilbert ℋ.