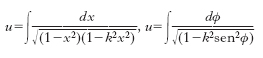amplitudine

Astronomia

Con riferimento a un astro si dicono, rispettivamente, a. ortiva l’arco di orizzonte compreso tra l’Est e il punto in cui l’astro sorge, a. occasa (o occidua) l’arco compreso tra l’Ovest e il punto in cui l’astro tramonta.

Matematica

Termine usato nella teoria dell’inversione degli integrali ellittici. L’integrale ellittico di prima specie può essere scritto nelle due forme:

la seconda ottenendosi dalla prima con il porre x=sen Φ. L’arco Φ si chiama anche a. di u; perciò la x, espressa in funzione di u, quale può essere ottenuta ricavandola dal primo dei due integrali con la cosiddetta inversione dell’integrale ellittico, risulta essere data dal seno dell’a. di u: x-sn u (leggi: seno amplitudine o senamplitudine). Tale estensione della terminologia trigonometrica è giustificata da diversi motivi. Qui basterà osservare che per k-0 la prima formula diventa:

ossia, a meno di una costante, u-arc sen x e quindi x-sen u; cioè la funzione trigonometrica seno si presenta come un caso particolare della funzione senamplitudine. Insieme a quest’ultima vengono poi considerate due altre funzioni:

dette rispettivamente coseno a. e delta a.; Le tre funzioni ora definite sono state prese a base dello studio delle funzioni ellittiche per circa mezzo secolo; espresso poi da C. Weierstrass l’integrale ellittico di prima specie in una forma diversa, ne è risultata una nuova base per la teoria (➔ inversione).