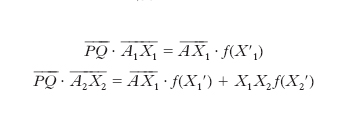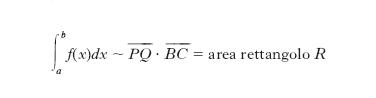integrale
In matematica, operazione eseguita su una funzione di variabile reale o complessa per determinare l’area delimitata dalla funzione stessa e dall’intervallo su cui è definita. Il termine s’incontra per la prima volta in uno scritto di G. Bernoulli (1690); le denominazioni di i. definito e i. indefinito sono usate invece nel Traité di S.-F. Lacroix (1799).
Calcolo integrale
Si intende quella parte della matematica, propriamente dell’analisi infinitesimale, fondata sull’operazione di integrazione, con la quale si determina il valore di una grandezza come somma di parti infinitesimali assunte in numero sempre crescente, così come il calcolo differenziale è basato sull’operazione di derivazione. Il problema classico da cui il calcolo i. ha avuto origine è quello della determinazione di aree e volumi di figure qualsiasi, mentre il calcolo differenziale a sua volta è stato originato dal problema della ricerca della pendenza della tangente a una linea in un suo punto. Il calcolo i. e il calcolo differenziale, almeno intesi in senso classico, appaiono come complementari tra loro, anche perché le due operazioni di derivazione e integrazione possono in certo senso riguardarsi come l’una l’inversa dell’altra (si ricorda, a questo proposito, il teorema di Torricelli-Barrow). Per un migliore inquadramento, anche storico, delle questioni di cui si occupa il calcolo integrale ➔ analisi. Di seguito sono riportati i principali tipi di i. e i più comuni metodi di integrazione, per lo più riferiti all’integrazione definita o indefinita.
I. definito. - Si supponga di avere una funzione f(x) reale, definita per tutte le x di un intervallo (a, b) limitato, e sia anch’essa limitata. Decomposto l’intervallo (a, b) in n parti di ampiezze Δx1, Δx2, ..., Δxn, indichiamo con e1′, e2′, ..., en′ gli estremi inferiori dei valori che la funzione assume nei singoli intervalli e calcoliamo la somma
σ′ = e1′Δx1 + e2′Δx2 + … + en′Δxn,
il cui valore dipende naturalmente dalla decomposizione scelta. Si considerino tutte le somme siffatte relative a tutte le possibili suddivisioni di (a, b) e per ciascuna di esse si indichi con δ la massima lunghezza degli intervalli di suddivisione. Per il lemma fondamentale della teoria dell’integrazione, la variabile σ′, al tendere a zero di δ (e quindi al tendere all’infinito di n), è convergente. Analogamente, le somme
σ″ = e1″Δx1 + e2″Δx2 + … + en″Δxn,
costruite con gli estremi superiori invece che inferiori, danno luogo a un’altra variabile convergente. Se i due limiti
sono uguali, la f(x) si dice integrabile nell’intervallo (a, b) e il loro valore comune è l’i. definito della f(x) esteso all’intervallo (a, b); esso si indica con la scrittura
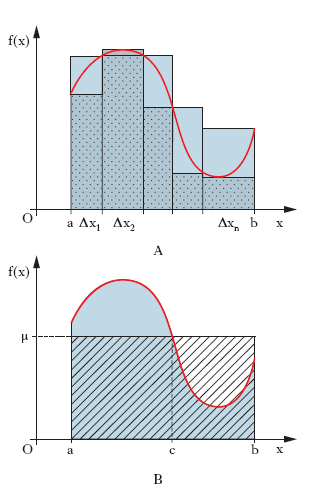
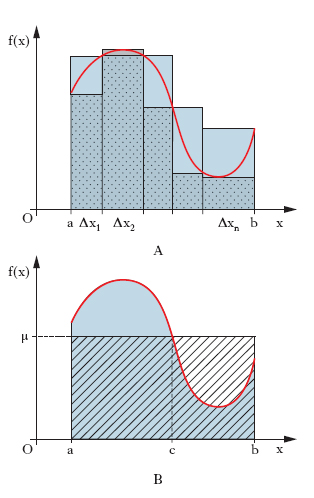
La funzione f(x) si chiama funzione integranda, la x è la variabile d’integrazione, a e b gli estremi d’integrazione. L’i. definito è suscettibile di una interpretazione geometrica che ne chiarisce il significato. Rappresentiamo la f(x) mediante il suo diagramma cartesiano (fig. 1 A): le somme σ′ e σ″ rappresentano allora le aree di figure come quelle evidenziate in fig. (scaloidi inscritti e circoscritti), ove si considerino come negative le aree al di sotto dell’asse x; il fatto che esse abbiano lo stesso limite consente di dire che la figura (rettangoloide) limitata dal diagramma della f(x), dall’asse x e dalle parallele a y per gli estremi dell’intervallo (zona colorata in grigio scuro in fig. 1 B) ha un’area che è data appunto dall’i. della f(x) esteso all’intervallo considerato. La matematica elementare permette, mediante addizioni e moltiplicazioni, di valutare quest’area solo in casi particolarissimi (per es., se f(x) è lineare, cioè nel caso di un rettangolo, di un triangolo o di un trapezio), mentre essa è determinabile, attraverso il procedimento infinitesimale sopra descritto, in casi ben più generali: basta, per es., che f(x) sia continua in tutto (a, b). La decomposizione del rettangoloide con rette parallele all’asse y porta ad avere dei valori comunque approssimati (nel caso dell’integrabilità) della sua area mediante le somme σ‘ e σ‘’, rispettivamente per difetto e per eccesso. Di questa decomposizione non resta traccia dopo il passaggio al limite che fornisce l’area esatta della figura nella sua interezza, onde il termine integrale. Una volta determinata l’area del rettangoloide, è ben evidente l’esistenza di un numero μ che sia l’altezza del rettangolo (zona rigata in fig. 1 B) che ha la stessa base del rettangoloide e gli è equivalente. Questo numero μ soddisfa alla condizione
e rappresenta una media dei valori che la funzione f(x) prende nell’intervallo (a, b); dalle ipotesi fatte sulla f(x) segue che esiste almeno un valore c dell’intervallo per il quale μ=f(c). La formula precedente diviene allora (teorema della media o del valor medio):
e la retta y=μ prende il nome di retta di compenso del rettangoloide. Se le variabili x e f(x) non hanno il significato di lunghezze, l’i. non rappresenta più un’area. Per es. se x è il tempo e f(x) la velocità, variabile con il tempo, di un punto mobile lungo una linea,
l’i. formula
dà il cammino percorso dal punto tra gli istanti a e b. Tuttavia, non appena ci serviamo della rappresentazione cartesiana per la f(x), l’i. definito fornisce l’area del rettangoloide come sopra spiegato. Per questo l’integrazione di una funzione di una variabile si dice anche quadratura. Supposto che f(x) sia integrabile, l’i. definito può ottenersi come limite, per δ → 0, anche di somme come le seguenti:
σ = f(x1)Δx1 + f(x2)Δx2 + … + f(xn)Δxn
dove x1, x2, ..., xn sono punti comunque scelti rispettivamente negli intervalli Δx1, Δx2, ..., Δxn (teorema di Darboux). Tuttavia il passaggio al limite presenta generalmente gravi difficoltà, ma la stessa analisi infinitesimale fornisce altri mezzi per calcolare l’i. definito, almeno in molti casi interessanti. Il simbolo ʃ proposto da G.W. Leibniz è la deformazione di una S, iniziale di Summa, e ricorda, insieme ai simboli f(x)dx che lo seguono, il significato dell’integrale. La nozione qui esposta di i. definito è sostanzialmente dovuta a P. Mengoli, A. Cauchy e B. Riemann; dell’i. di Mengoli-Cauchy-Riemann si conoscono varie generalizzazioni tra cui, particolarmente notevoli, l’i. secondo H. Lebesgue e l’i. secondo T.J. Stieltjes.
I. di campo o multiplo. - Il concetto di i. definito può essere trasportato alle funzioni di due, tre, quattro ..., n variabili, definendo l’i. esteso a una regione A del piano, dello spazio a tre, quattro, ..., n+1 dimensioni, rispettivamente; esso prende il nome di i. di campo e più particolarmente i. doppio, triplo ecc.; la regione A si chiama campo o dominio di integrazione. I simboli usati sono,
oppure
o anche:
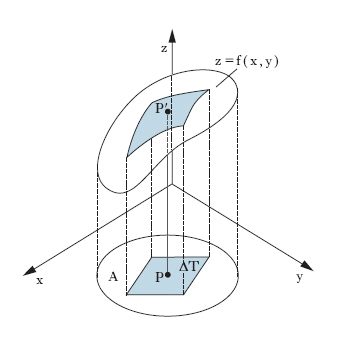
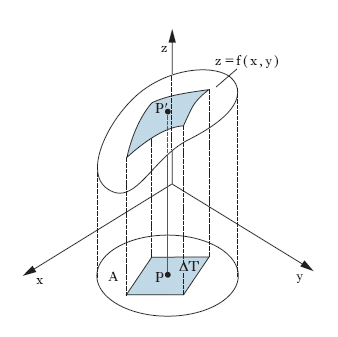
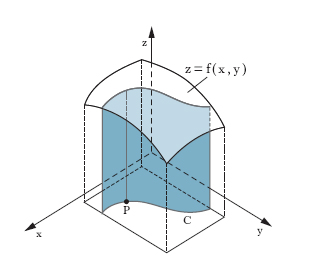
Prescindendo dai casi di non integrabilità, l’i. di campo risulta il limite, per δ → 0, di somme del tipo σ=f(P1)ΔT1+f(P2)ΔT2+...+ f(Pn)ΔTn, ove ΔT1, ΔT2, ..., ΔTn sono le aree, oppure i volumi ... degli elementi di una decomposizione di A; P1, P2, ..., Pn sono punti, comunque scelti, rispettivamente, in detti elementi; e δ è, per ogni decomposizione, il massimo diametro dei ΔTi. Se diamo alle variabili x, y, f(x, y) il significato di lunghezze, l’i. doppio dà un volume, precisamente quello del cilindroide limitato dalla superficie di equazione cartesiana z=f(x, y), dal piano xy e dalla superficie cilindrica a generatrici verticali avente per direttrice sul piano xy il contorno della regione A (fig. 2). Per questo un’integrazione doppia si dice anche una cubatura. Per l’i. triplo l’analoga interpretazione viene meno nello spazio ordinario, ma si può dare in uno spazio a quattro dimensioni. Si noti che l’i. doppio della funzione costante 1, rappresentando il volume di un cilindro di altezza 1, dà la misura della base (come l’i. definito della funzione 1, esteso all’intervallo (a, b), dà la misura di questo). Analogamente l’i. triplo della funzione 1, pensata adimensionale, dà il volume della regione a cui è esteso. Così, per es., se C è il cerchio del piano xy e S la sfera, ambedue con il centro nell’origine degli assi e raggio r, per il volume V della sfera si ha
V = 2 ∫∫C √‾‾‾‾‾‾r2 − x2 ‾‾‾− y2‾‾‾‾ dxdy = ∫∫∫S dxdydz.
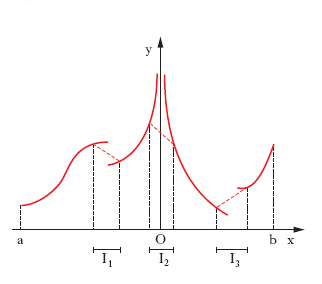
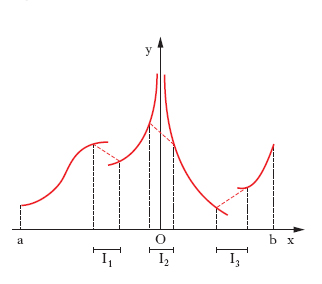
I. di Lebesgue. - È una generalizzazione del concetto di i. di una funzione reale di punto. L’importanza della generalizzazione sta nel fatto che l’i. di Lebesgue si può definire per le funzioni quasi continue anche illimitate in un insieme, che può essere limitato o no. Nel caso più semplice di una funzione quasi continua y=f(x) di una variabile reale x, definita in un intervallo (a, b) (fig. 3), la definizione si può dare come segue: per ogni intero naturale n si scelga in (a, b) una successione di intervalli parziali (I1, I2, I3 in fig. 3) tali che: a) siano privi a due a due di punti interni comuni; b) abbiano lunghezza globale non superiore a 1/n; c) nell’insieme dei punti non interni a tali intervalli la f(x) sia continua. Nei punti interni a tali intervalli si sostituisca la f(x) con una funzione lineare, che coincida con la f(x) negli estremi dei singoli intervalli (segmenti tratteggiati rossi in fig. 3); si ottiene così una nuova funzione (continua) fn(x). Orbene, se il
è determinato, il suo valore si chiama i. di Lebesgue della f(x) esteso ad (a, b) e si indica con
La definizione di i. di Lebesgue è stata ulteriormente generalizzata in varie direzioni, soprattutto sostituendo allo spazio ambiente euclideo uno spazio metrico o topologico.
I. di Stieltjes. - Si può considerare un’estensione dell’i. di Lebesgue. È una generalizzazione del concetto di i. definito, ottenuta sostituendo alla variabile d’integrazione una opportuna funzione. Nel caso delle funzioni di una sola variabile, date in un intervallo (a, b) due funzioni reali, g(x) continua e F(x) a variazione limitata, l’i. di Stieltjes è definito da:
ove x0=a, x1, ..., xn−1, xn=b è una divisione di (a, b) in intervalli parziali, ξi è un punto scelto nell’intervallo (xi–1, xi), e il limite è eseguito facendo tendere a zero la massima ampiezza degli intervalli.
I. curvilineo. - L’i. curvilineo di una funzione di più variabili, definita in una certa regione, esteso a un arco di curva C giacente nella stessa regione, si indica con il simbolo
o altri equivalenti; è dato dal
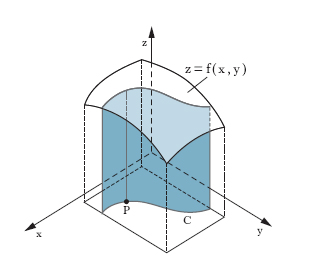
limite delle somme dei prodotti delle lunghezze di elementi dell’arco per i valori che la funzione assume in punti degli stessi archetti; se, in particolare, C appartiene al piano xy (fig. 4) e la funzione f, sostituita ora da una funzione di due variabili z=f(x, y), non è mai negativa su C, l’i. curvilineo fornisce l’area della porzione di superficie (cilindrica) descritta da un segmento perpendicolare al piano xy, con piede P su C e lunghezza f(x, y), al variare di P su C. Poggiando su questo concetto si può definire anche l’i. di una funzione di variabile complessa (o i. nel campo complesso) esteso a una linea C del piano complesso.
I. superficiale. - È l’analogo dell’i. curvilineo, esteso però a una porzione S di superficie dello spazio. L’i. superficiale di una funzione è indicato con il simbolo 1.7
I. indefinito. - I. indefinito di una funzione f(x), integrabile, di una sola variabile, è l’insieme di tutte le funzioni primitive della f(x), cioè delle funzioni F(x), G(x), ... la cui derivata F′(x), G′(x), ... è f(x); si indica con
tali funzioni differiscono tra loro per una costante additiva arbitraria c; cioè se F(x) è una di esse, tutte le altre sono date da F(x)+c. Una funzione primitiva è data
dall’i. formula,
essendo a fisso e intendendo tale i. come funzione del suo estremo superiore x (teorema di Torricelli-Barrow). Questo fatto, oltre a mettere in stretta relazione il calcolo i. e il calcolo differenziale, fornisce un mezzo per il calcolo degli i. definiti. Infatti, appena sia nota una primitiva F(x) della funzione f(x), avendosi necessariamente
e quindi formula,
l’i. definito
è praticamente calcolato. Per la differenza F(b)−F(a) si suole adottare la scrittura [F(x)]ba. Osserviamo poi che l’operazione di integrazione indefinita permette di costruire, a partire da una data funzione f(x), una nuova funzione F(x) (la sua primitiva), e si può quindi pensare come un’operazione generatrice di nuove funzioni. Questo perché prendendo la f(x) in un certo ambito di funzioni (per es., funzioni elementari), di regola la F(x) appartiene a un ambito più elevato e non è pertanto esprimibile mediante funzioni dell’ambito cui appartiene la f(x).
1.8 I. generalizzato o improprio. - È l’i. definito, calcolato attraverso appropriati passaggi al limite, di una funzione non limitata; oppure l’i. esteso a un insieme non limitato. Per es.:
1.9 I. stocastico. - I. eseguito rispetto a una misura indotta da un processo stocastico. Tale nozione si differenzia dall’usuale integrazione rispetto a una data densità quando il processo non è a incrementi indipendenti.
Per i. funzionale o i. sui cammini (➔ cammino).
Integrazione delle funzioni di una variabile
È il problema della ricerca dell’i. indefinito di una funzione f(x). Il detto i. è costituito dall’insieme delle funzioni che ammettono la f(x) come derivata: l’integrazione è quindi immediata quando la f(x) è la derivata di una delle funzioni elementari xn, ex, logx, senx ecc. Ciò significa che la tabella delle derivate fondamentali fornisce in modo immediato anche la seguente tabella di i. indefiniti (nella quale c rappresenta una costante arbitraria):
Partendo dai precedenti i., è possibile calcolarne altri per via elementare, servendosi delle seguenti regole di integrazione:
a) formula
essendo k una costante (cioè una costante moltiplicativa può essere «portata fuori» del segno di integrazione). b) Integrazione per decomposizione in somma:
,
cioè «l’i. di una somma è la somma degli i. degli addendi». c) Integrazione per parti:
a parole: «l’i. del prodotto del fattore finito f(x) per il fattore differenziale g′(x)dx è uguale al prodotto del fattore finito per l’i. g(x) del fattore differenziale meno l’i. del prodotto dell’i. trovato, g(x), per il differenziale del fattore finito, f′(x)dx». La formula è utile quando accada che l’i. a secondo membro sia di calcolo immediato senza che ciò avvenga per quello a primo membro, oppure che si ripeta al secondo membro lo stesso i. che compare al primo membro, ma con coefficiente diverso, di modo che esso possa ottenersi risolvendo algebricamente l’espressione. d) Integrazione per sostituzione: con una sostituzione della variabile d’integrazione, cioè con la posizione x=ϕ (t), e quindi dx=ϕ′(t)dt, l’i. diventa
e può darsi che la nuova funzione sia facilmente integrabile. L’i. indefinito risulterà espresso in funzione della variabile t; occorrendo, lo si potrà esprimere in funzione della x operandovi la sostituzione t=τ(x), inversa della x=ϕ(t).
Le regole a) e b) permettono già di calcolare l’i. di una funzione razionale intera (polinomio). Anche l’i. di una funzione razionale fratta (quoziente di polinomi) si può esprimere mediante un numero finito di termini, tra i quali figurano soltanto delle funzioni razionali e le trascendenti elementari logaritmo e arcotangente. Quando però si esce dal campo delle funzioni razionali, l’integrazione conduce di solito a nuove funzioni trascendenti, non riducibili a quelle elementari.
Tra gli altri procedimenti di integrazione ricordiamo l’integrazione per serie: in un intervallo (a, b) si abbia
formula;
f(x) sia cioè espressa come
somma di una serie di funzioni, la quale sia uniformemente convergente nell’intervallo (a, b); se esistono gli i.
,
si ha:
per tutti gli x di (a, b). Se, della serie a secondo membro, si prende la somma di un numero finito di termini, si ottiene un valore approssimato dell’integrale. Questo procedimento è largamente impiegato quando l’i. non sia facilmente esprimibile in altro modo, ma si possieda uno sviluppo in serie della funzione integranda che procede per funzioni di tipo semplice.
Integrazioni delle funzioni di due o più variabili
Tra i metodi di integrazione definita delle funzioni di due variabili ricordiamo la riduzione di un i. doppio a due i. semplici successivi. Si supponga di dover calcolare l’i. doppio
,
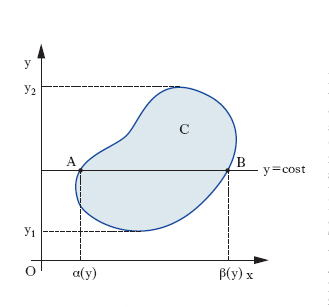
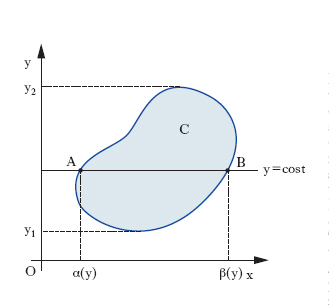
essendo la funzione reale f(x, y) continua nel campo C del piano xy; e si supponga che il campo C soddisfi le seguenti condizioni (fig. 5): a) la proiezione di C sull’asse y sia un intervallo (y1, y2); b) ogni retta y=cost compresa tra le y=y1 e y=y2 abbia in comune con C un segmento i cui estremi A e B appartengano al contorno di C; c) le ascisse di A e B siano due funzioni α(y), β(y) continue in tutto l’intervallo (y1, y2). In queste ipotesi vale il teorema di riduzione dell’integrazione doppia a due integrazione semplici successive, espresso dalla formula .
Il teorema naturalmente si può estendere alle funzioni di più variabili.
Integrazione numerica
Il valore di un i. definito si può approssimare anche con soli calcoli numerici. Già la definizione stessa di i. definito o, meglio ancora, la proprietà espressa dal teorema di Darboux suggerisce la formula
ove i Δxi sono gli intervalli di una suddivisione di (a, b) e xi è un punto comunque scelto in Δxi. Esistono naturalmente metodi ben più efficienti che consistono nell’approssimare la y=f(x) nell’intervallo (a, b) mediante dei polinomi interpolatori che assumono, per i valori x1, ..., xn+1 della variabile x, certi n+1 valori prefissati y1, y2, ..., yn+1, e quindi nell’integrare tali polinomi. Così, mediante una combinazione lineare dei valori della funzione da integrare, detta formula di quadratura, con coefficienti dipendenti dal grado del polinomio interpolatore, si ottiene un valore approssimato dell’i., tanto più vicino al valore vero quanto migliore è l’approssimazione della funzione per mezzo del polinomio. Una delle formule di quadratura più usate si ricava suddividendo l’intervallo (a, b) dell’asse x in n intervalli (x0, x1), ..., (xn−1, xn), con passo s=xi+1−xi costante, e integrando la formula di di Gregory-Newton rispetto alla variabile h, con h=(x−x0)/(x1−x0); in tal modo si ha:
dove Δ1, Δ2, ... sono le cosiddette differenze successive della suddetta interpolazione. A seconda del valore di n, si hanno diverse formule di quadratura. Per n=1, approssimando cioè la funzione da integrare con una retta, si ottiene la formula
d’integrazione trapezoidale:
per n=2, approssimando cioè la funzione da integrare con archi di parabola passanti per tre punti, (x0, y0), (x1, y1), (x2, y2) e sommando i risultati ottenuti in ciascuno degli intervalli (x0, x2), (x2, x4), (xn−2, xn) si ottiene la formula
di Cavalieri-Simpson.
Per n=3 si ha la formula di Newton-Cotes. Più in generale è possibile ottenere delle formule di integrazione, a partire da altre forme del polinomio interpolatore (per es., polinomi di Lagrange, di Hermite, di Legendre ecc.). Le formule viste prevedono la suddivisione dell’intervallo di integrazione in parti uguali; tale limitazione può essere evitata facendo uso delle formule di integrazione di Gauss. Tali formule sono caratterizzate dal fatto che l’intervallo è diviso tramite punti x1, x2, ..., xn−1 non equidistanti, scelti opportunamente tra gli estremi di integrazione, in modo da migliorare al massimo la precisione della formula. A tal fine è opportuno trasformare l’i. definito (v. formula)
nella forma
in cui
g(x)=f(x)/p(x) con p(x) funzione peso, tale che p(x) ≥ 0 in (a, b). Facendo uso della formula di interpolazione di Hermite, a meno del resto, si ottiene:
Le ascisse x1, x2, ..., xn vengono determinate in modo che i coefficienti Bi che moltiplicano le derivate g′(x) risultino nulli; ciò si ottiene scegliendo le ascisse coincidenti con gli zeri di una famiglia di polinomi P0(x), P1(x), ..., Pn(x) che rispetto a p(x) nell’intervallo (a, b) verifichino le relazioni
se m≠n
Tali polinomi vengono perciò detti ortogonali, nell’intervallo (a, b), rispetto alla funzione peso p(x). I coefficienti Ai sono dati dalla relazione:
dove Pn(x)=anxn+an–1xn–1+...+a0 è il polinomio di grado n della successione P0(x), P1(x), ..., Pi(x), e qn–1 è definito dalla [1]. La costruzione di una formula di quadratura di tipo gaussiano procede quindi attraverso i seguenti passi: 1) per il dato intervallo (a, b) di integrazione, si fissa il numero n dei punti sull’asse x; 2) si sceglie il polinomio del sistema ortogonale e di conseguenza la funzione peso p(x); 3) si calcolano le radici x1, x2, ..., xn del polinomio; 4) si ricavano dalla [2] i valori dei coefficienti Ai. Esistono diverse formule di quadratura gaussiane a seconda del polinomio P(x) scelto e della relativa funzione peso, tra le quali si ricordano quelle riportate in tabella: per ciascuna di esse sono indicati l’intervallo d’integrazione, le espressioni del polinomio ortogonale P(x), della funzione peso p(x), e dei coefficienti Ai. La scelta del metodo numerico per il calcolo di un i. definito dipende da diversi elementi, quali la precisione richiesta, il modo in cui è data la funzione da integrare, la disponibilità dei mezzi di calcolo.
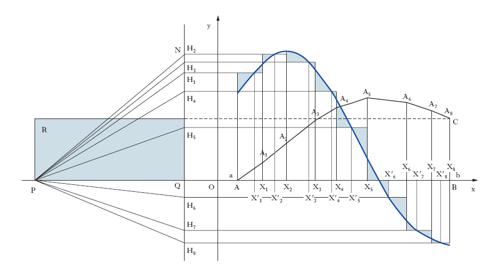
Integrazione grafica
La somma del teorema di Darboux può essere valutata con una costruzione grafica, come la seguente. Tracciato, in scale adatte, il grafico cartesiano della funzione y=f(x), suddiviso l’intervallo AB=(a, b) in parti (non necessariamente uguali) mediante i punti X1, X2, ... (fig. 6) e condotte per detti punti le rette verticali, si scelga in ogni intervallo Xi–1 Xi un punto Xi′. Le ordinate della funzione nei punti così scelti si riportano sulla retta QN, ottenendo i segmenti QH1, QH2, ... Indi, fissato un punto P sull’asse x, si traccia per A la parallela a PH1, fino all’incontro A1 con la verticale per X1; per A1 la parallela a PH2 fino all’incontro A2 con la verticale per X2, ... si ha che
e, in definitiva:
La scelta dei punti Xi′ è lasciata all’abilità del disegnatore: tanto meglio per l’approssimazione se le areole tratteggiate al di sopra e al di sotto del diagramma si equivalgono. Come la derivazione grafica, l’integrazione grafica ha oggi interesse storico, essendo i processi grafici soppiantati da quelli numerici.
Integrazione meccanica
Speciali apparecchi detti planimetri misurano l’area di una figura piana percorrendone il contorno. Altri strumenti, gli integrafi, venivano usati per tracciare la curva i. di una curva data: facendo percorrere a un indice il diagramma di una funzione, una punta scrivente tracciava la linea integrale. Un tipo particolare di integrafi sono gli integrometri, usati per il calcolo di momenti statici e di momenti d’inerzia di una figura piana rispetto a una retta del suo piano.

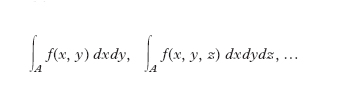
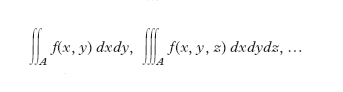
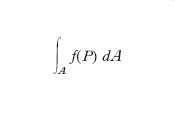
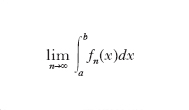
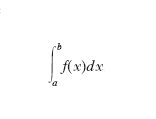
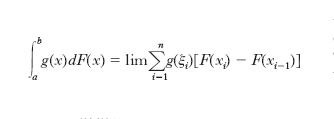
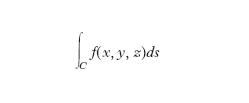
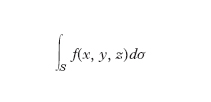
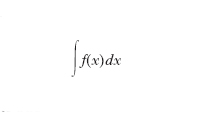
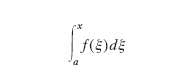
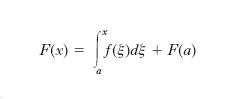
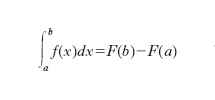
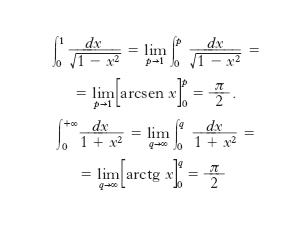

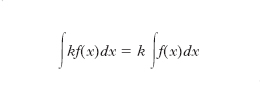
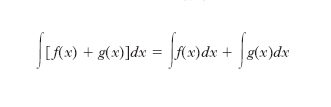
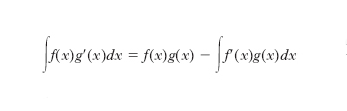
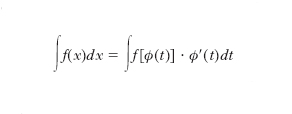
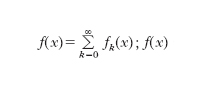
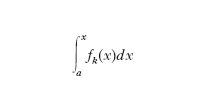
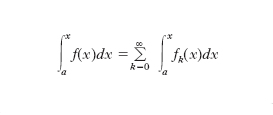
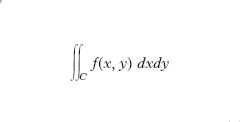
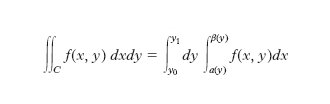
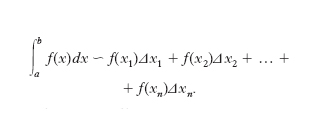
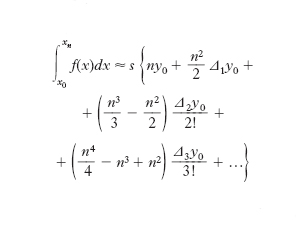
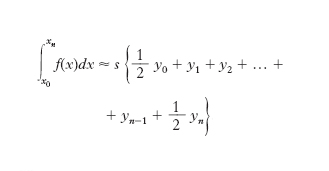
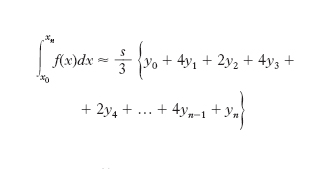
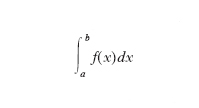
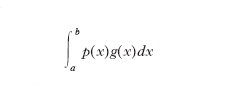
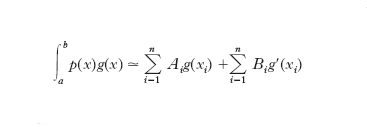
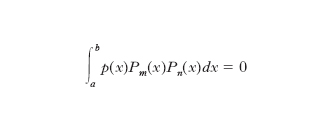
![[1]](https://images.treccani.it/ext-tool/intra/thumbs_medium/5/52/FORMULE_integrale_38_1.jpg)
![[2]](https://images.treccani.it/ext-tool/intra/thumbs_medium/2/2c/FORMULE_integrale_39_2.jpg)