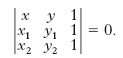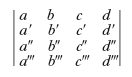retta
Ente geometrico fondamentale, in genere assunto come primitivo nelle trattazioni assiomatiche.
Astronomia
R. d’altezza Proiezione di un tratto del cerchio d’altezza (➔ cerchio) sopra una carta di Mercatore. Le r. d’altezza sono utilizzate per le determinazioni del punto.
Economia
R. del bilancio del consumatore, della spesa o dei prezzi Luogo dei punti corrispondenti alle varie combinazioni quantitative di due beni che, dati i prezzi dei beni stessi, il consumatore può acquistare con un dato reddito.
Matematica
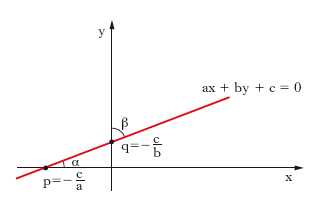
La nozione di r., insieme con quella di punto e con altre, fa parte delle nozioni primitive: rinunciando a ogni definizione a carattere descrittivo, ci si limita ad assegnare un gruppo di assiomi o postulati che costituiscono una definizione implicita della r., del punto, del piano ecc. (➔ geometria). Per essa valgono le seguenti proprietà: per due punti distinti A e B (nel piano come nello spazio) passa una e una sola retta (che viene solitamente indicata con la notazione AB); il tratto di retta (segmento) compreso tra A e B rappresenta il cammino più breve che collega A e B; dati un punto P e una retta a, per P passa una e una sola retta parallela (oppure perpendicolare) ad a (quest’ultima proprietà vale solo nella geometria euclidea). In un sistema di assi cartesiani nel piano (v. fig.) una r. è rappresentata da una equazione algebrica di 1° grado in x e y:
[1] formula
dove a, b, c sono tre coefficienti non tutti nulli, di cui a, b, mai contemporaneamente nulli, e x, y sono le coordinate di un punto variabile sulla retta. L’equazione di una r. ha nei diversi sistemi di riferimento forme diverse; nel caso particolare di un sistema di assi cartesiani x, y ortogonali, la r. è data mediante l’equazione [1] e i suoi coseni direttori (cioè i coseni degli angoli α e β che la r. forma rispettivamente con l’asse x e con l’asse y), sono dati dalle formule:
mentre i coseni direttori di una r. normale alla retta data sono espressi da:
(dove, sia per i primi coseni sia per i secondi, il segno del denominatore resta determinato dall’orientamento della r.). Operando opportunamente sull’equazione [1], essa si può scrivere nella forma:
[2] formula
dove d rappresenta la distanza dell’origine O degli assi dalla r. data. L’equazione [2] è anche nota con il nome di equazione di Hesse. La r. che incontra gli assi coordinati nei punti (p, 0), (0, q) ha equazione:
[3] formula
La [3] è detta equazione segmentaria di una retta. Infine, la r. che passa per i punti P1(x1, y1), P2(x2, y2) ha equazione:
[4] formula
Nello spazio, una r. si rappresenta per solito come intersezione di due piani e quindi mediante le equazioni generali
[5] formula
o mediante le equazioni ridotte
[6] formula
o ancora, forma da preferirsi quando la r. è assegnata mediante i punti P1(x1, y1, z1), P2(x2, y2, z2), con le equazioni
[7] formula
I numeri direttori (o parametri direttori) l, m, n sono dati, nel caso [5], da quantità proporzionali a bc′–b′c, ca′–c′a, ab′–a′b; in [6] sono l, m, 1 e infine nella [7] sono i tre denominatori. Due r. di parametri l, m, n e l′, m′, n′ sono parallele se l/l′=m/m′=n/n′, mentre sono perpendicolari se ll′+mm′+nn′=0. In generale, l’angolo ϑ tra le due rette è individuato dalla relazione:
dove il segno del denominatore dipende dall’orientamento attribuito alle rette. Le due r. di equazioni ax+by+cz+d=0, a′x+… +d′=0 e a″x+ … +d″=0, a‴x+ … +d‴=0 sono complanari o sghembe a seconda che il determinante
sia rispettivamente uguale a zero o diverso da zero.
Con particolari qualificazioni, il termine r. assume diversi significati. R. caratteristica Per un sistema ∞1 di piani, è quella r. di uno qualunque di essi che si ottiene come limite dell’intersezione di detto piano con un altro piano del sistema il quale tenda a coincidere con il primo. R. complessa (o immaginaria) R. del piano per la quale i mutui rapporti dei coefficienti non sono tutti reali; nello spazio è una r. che non si può ottenere come intersezione di due piani reali. Una r. complessa dello spazio è detta di prima specie se contiene un punto reale, di seconda specie se non ne contiene alcuno. R. orientata R. su cui è fissato un verso di percorrenza. R. ortogonali Nello spazio, sono due r. tali che esista un piano passante per l’una e ortogonale all’altra. R. parallele Nella geometria euclidea, sono r. di un piano che non hanno un punto comune; nella geometria affine sono r. che s’incontrano in un punto improprio. R. proiettiva R. euclidea completata con un punto improprio, da considerarsi alla stessa stregua degli altri punti; astrattamente è l’insieme delle coppie di numeri (x0, x1) (reali o complessi, a seconda che tale sia la r.), non entrambi nulli, definiti a meno di un comune fattore di proporzionalità non nullo. R. reale R. del piano i cui coefficienti sono reali, ovvero r. dello spazio che si può ottenere come intersezione di due piani reali. R. tangente Rispetto a una curva o a una superficie, è il limite della congiungente due punti della curva o della superficie, i quali tendano a coincidere (➔ tangente).