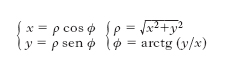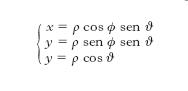coordinate

Astronomia

fig. 1

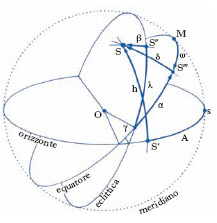
C. celesti Coppia di parametri (precisamente, coppia di angoli) atti a individuare la posizione di un astro sulla sfera celeste o, se si vuole, atti a individuare un punto della sfera stessa. Si tratta di c. curvilinee sferiche, che vengono definite nel modo seguente. Si sceglie sulla sfera celeste di centro O (fig. 1) un cerchio massimo a, detto cerchio base, e su esso si sceglie un punto A, origine, e un verso di percorrenza; si assume poi come positivo uno dei due emisferi in cui a divide la sfera. Ciò fatto, se S è un punto della sfera celeste, si traccia la minima distanza sferica di S da a, cioè si conduce per S un arco c di cerchio massimo ortogonale ad a sino a incontrare a medesimo in S′. Si chiama allora ascissa sferica di S il valore ϑ dell’angolo AOS′ e ordinata sferica di S quello ψ dell’angolo S′OS. Linee coordinate sono dunque, da un lato, a e tutti i cerchi paralleli a esso e, dall’altro, tutti i cerchi ortogonali ad a.

fig. 2

C. altazimutali (od orizzontali) Cerchio base è l’orizzonte (fig. 2), origine è il punto Sud, s, dell’orizzonte, verso positivo è quello orario visto dallo zenit e come emisfero positivo è assunto quello contenente lo zenit. L’ascissa A (ampiezza dell’arco sS′, usualmente espressa in gradi sessagesimali) ha il nome di azimut, l’ordinata h (ampiezza dell’arco S′S, usualmente espressa in gradi sessagesimali) è detta altezza (e il complemento distanza zenitale). Tale sistema, molto usato in topografia e in geodesia, lo è assai meno in astronomia perché azimut e altezza variano al variare della posizione dell’osservatore e, a causa del moto diurno della sfera celeste, variano nel corso della giornata, indipendentemente dal moto proprio di S sulla sfera stessa.

C. eclitticali (o eclittiche) Cerchio base è l’eclittica (fig. 2), origine è il punto vernale γ, verso positivo per le ascisse è il verso antiorario visto dalla normale dell’emisfero positivo, che è quello contenente il polo dell’eclittica. L’ascissa λ (ampiezza dell’arco γ S″, usualmente espressa in ore, essendo 1^h = 15°) si chiama longitudine celeste, mentre l’ordinata β (ampiezza dell’arco S″S, usualmente in gradi sessagesimali) si chiama latitudine celeste. Tale sistema era particolarmente usato dagli antichi astronomi.

C. equatoriali Cerchio base è l’equatore celeste (fig. 2), origine è il punto vernale γ, verso positivo sull’equatore è quello diretto ed emisfero positivo è quello boreale, cioè quello contenente il polo Nord celeste. L’ascissa α (ampiezza dell’arco γS″, in ore) ha il nome di ascensione retta, e l’ordinata δ (ampiezza dell’arco S‴S, in gradi sessagesimali) quello di declinazione. Tale sistema è quello comunemente usato. C. galattiche Sistema, particolarmente usato nell’astronomia stellare statistica, che assume come cerchio base l’equatore galattico, come origine l’intersezione di questo con l’equatore celeste, mentre il verso positivo è, al solito, quello diretto e l’emisfero positivo è quello contenente il polo Nord galattico.

C. orarie (fig. 2) Sistema di c. analogo a quello equatoriale, salvo il verso di percorrenza sull’equatore, che è quello orario e non quello diretto, e l’origine delle ascisse, che non è il punto vernale γ ma il mezzocielo M, cioè quella delle due intersezioni dell’equatore celeste con il cerchio meridiano che risulta al di sopra dell’orizzonte. L’ordinata, naturalmente, è sempre la declinazione, mentre l’ascissa ω (ampiezza dell’arco MS‴) si chiama angolo orario e, a differenza dell’ascensione retta, dipende dalla posizione dell’osservatore.

Fisica

C. colorimetriche Terna di parametri che, in relazione a un particolare «triangolo di colore», individuano un colore (➔ cromatica).

Geografia

C. terrestri

Le c. terrestri sono una coppia di parametri, e precisamente una coppia di angoli, atti a individuare la posizione di un punto P sulla superficie terrestre, intendendo come tale la superficie del geoide, vale a dire la superficie libera media dei mari; per individuare completamente la posizione di P occorre aggiungere alle due c. anzidette, che hanno il nome di latitudine e longitudine, una terza c., e precisamente l’altezza sul mare, o altitudine, distanza tra la superficie di livello della gravità per P e la superficie del geoide, misurata lungo la verticale per P. In pratica, quando si parla di c. di un punto della Terra, ci si riferisce abitualmente soltanto alla latitudine e alla longitudine.

fig. 3

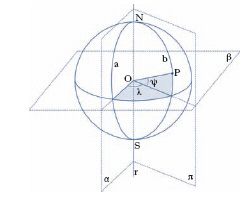
Sistemi di coordinate. - Si hanno vari sistemi di c., più o meno riducibili a sistemi di c. polari, i quali hanno alcuni elementi in comune e si diversificano per altri. Gli elementi in comune sono costituiti dal piano equatoriale (piano ortogonale all’asse della rotazione terrestre, condotto per il centro della Terra), al quale vengono comunque riferite le latitudini, e dalla località di Greenwich, presso Londra, alla quale abitualmente si fa riferimento per le longitudini. Le c. geocentriche sono un sistema di c. polari in senso stretto, nel quale si assume l’asse r della rotazione terrestre come asse polare (fig. 3), il centro O della Terra come polo, e il semipiano α uscente da r e passante per Greenwich come semipiano polare: la latitudine geocentrica di un punto P è l’angolo ψ che il raggio vettore OP forma con il piano equatoriale β (seguita dalla qualifica N oppure S a seconda che P appartenga all’emisfero Nord o a quello Sud), e la longitudine geocentrica di P è l’angolo λ che il semipiano π uscente da r e contenente P, forma con il semipiano polare α, contato da 0° a 180° a partire da α verso E o verso O: λ è seguita dalla qualifica E (East) oppure W (West). Si viene a stabilire sul geoide, in tal modo, un sistema di c. curvilinee, in cui linee coordinate sono da un lato le linee di equazione ψ = costante, dall’altro le linee di equazione λ = costante: queste ultime, dette meridiani, sono le intersezioni del geoide con i semipiani uscenti da r (l’intersezione a determinata da α è il meridiano fondamentale, quella b determinata da π è il meridiano locale di P), mentre le prime, dette paralleli, sono le intersezioni del geoide con il cono di vertice O e semiapertura 90°−ψ, e quindi, in generale, sono linee chiuse non piane. I due sistemi di linee si intersecano sotto angoli diversi (i meridiani intersecano però ortogonalmente l’equatore), formando nel complesso un reticolato a maglie quadrangolari (reticolato geografico).

fig. 4

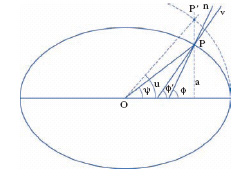
Poiché il geoide è assimilabile, con ottima approssimazione, a un ellissoide di rivoluzione intorno all’asse della rotazione terrestre, poco schiacciato, il sistema di c. terrestri usato nella pratica, le c. geografiche propriamente dette (talora indicate però come c. geodetiche), fa riferimento appunto alla superficie di un ellissoide, il cosiddetto ellissoide geodetico (o internazionale), di dimensioni fissate per convenzione internazionale in modo da approssimare nel miglior modo possibile la superficie del geoide. La longitudine geografica del generico punto P coincide, naturalmente, con la longitudine λ prima definita; le linee di ugual longitudine, i meridiani geografici, sono però stavolta linee di forma semplice, e precisamente ellissi uscenti dai poli terrestri, intersezioni dell’ellissoide con piani per l’asse della rotazione terrestre. La latitudine geografica di P viene poi definita come l’angolo ϕ (fig. 4) che la normale n in P all’ellissoide geodetico forma, al solito, con il piano equatoriale, le linee di ugual latitudine, cioè i paralleli geografici, sono circonferenze parallele all’equatore. Il reticolato geografico assume quindi un carattere di regolarità, che mancava nel sistema di c. geocentriche e che ha fondamentale importanza per le esigenze della cartografia.

Con l’esperienza non può determinarsi direttamente nel generico punto P né la direzione della normale n all’ellissoide geodetico, occorrente per determinare ϕ, né la direzione del raggio vettore OP, occorrente per determinare ψ: quel che può essere direttamente determinato con l’esperienza (e in concreto con livelle e col filo a piombo) è la giacitura del piano tangente in P al geoide, cioè del piano orizzontale per P, o, che è lo stesso, la direzione della normale in P al geoide, vale a dire la verticale v per P, il cui punto all’infinito è lo zenit Z di P. Si definisce pertanto, con riferimento alla verticale v, un’altra coppia di c., dette c. astronomiche in quanto per la loro determinazione ci si serve di strumenti e di metodi propri dell’astronomia di posizione. Precisamente, la longitudine astronomica λ′ ha una definizione analoga a quella della longitudine geografica λ, salvo il fatto che ora ci si riferisce non al piano del meridiano geografico ma al piano del meridiano astronomico per P, cioè al piano contenente la verticale v per P e parallelo all’asse r della rotazione terrestre; quanto alla latitudine astronomica, essa è l’angolo ϕ′, che v forma con il piano equatoriale β. È chiaro che λ′ e λ coincidono se v incontra r, e che ϕ′ e ϕ coincidono se v coincide con la normale n all’ellissoide internazionale. La determinazione delle differenze, assai piccole e normalmente trascurabili ai fini pratici, tra c. astronomiche e geografiche, le cosiddette deviazioni dalla verticale (dalla normale all’ellissoide geodetico), costituisce uno dei compiti della geodesia.

Per facilitare il cosiddetto trasporto delle c., problema di fondamentale importanza nella geodesia e nella topografia, si introducono anche altre c. come le c. geodetiche polari e rettangolari. Da ricordare inoltre la cosiddetta latitudine ridotta u, definita nel modo seguente: si immagini tracciata per il generico punto P la parallela a all’asse della rotazione terrestre sino a incontrare in P′ la superficie sferica di centro O e raggio pari al semiasse equatoriale dell’ellissoide geodetico: u è allora l’angolo che il raggio vettore OP′ forma con il piano equatoriale.

Determinazione diretta delle c. di un punto. - Si effettua, come già accennato, con metodi astronomici. Precisamente, il metodo correntemente usato per la determinazione della latitudine consiste nel misurare l’altezza h sull’orizzonte di un astro, la cui declinazione δ sia nota, nell’istante in cui esso transita al meridiano del luogo (in luogo di h, può essere misurato il suo complemento, cioè la distanza zenitale z): ϕ si ricava dalla relazione ϕ−δ=90°−h=z. È il metodo che si segue, per es., in marina per fare il ‘punto’, rilevando col sestante l’altezza del Sole nell’istante del mezzogiorno vero (le tavole di effemeridi nautiche forniscono, giorno per giorno, il valore di δ e l’istante del passaggio al meridiano, in tempo di Greenwich). Per determinazioni più accurate si seguono metodi più raffinati basati sulla misurazione dell’altezza di stelle circumpolari, effettuata con cannocchiali meridiani e corretta delle varie cause di errore (flessione dello strumento, rifrazione atmosferica ecc.). Per quanto riguarda la longitudine, la determinazione si effettua in base al principio che la differenza di longitudine tra due punti A, B della superficie terrestre (A, in particolare, può essere Greenwich) è pari alla differenza tra i tempi siderali in A e in B (in base alla corrispondenza di 1 ora con 15° di longitudine). Il tempo siderale t_s locale è pari all’ascensione retta a di un astro qualunque nell’istante del suo passaggio al meridiano, di modo che è direttamente determinabile con un cannocchiale meridiano e con l’ausilio di tavole di effemeridi, la conoscenza del tempo siderale t_s′ di Greenwich è sufficiente allora per determinare la longitudine locale. Nel passato, t_s′ veniva determinato esclusivamente in base alle indicazioni di un orologio inizialmente regolato sul tempo locale di Greenwich (la realizzazione di cronometri da marina che «conservavano» con sufficiente esattezza tale tempo durante le lunghe navigazioni oceaniche costituì uno dei fattori determinanti per le grandi crociere geografiche dei sec. 18° e 19°); attualmente, ci si basa anche sulla ricezione di segnali orari emessi da apposite stazioni radiotrasmittenti.

Variazione delle coordinate. - Elemento costante di riferimento per le c. terrestri, e in particolare per le latitudini, è il piano equatoriale terrestre o, in modo equivalente, l’asse della rotazione terrestre. Poiché tale asse non si mantiene costantemente parallelo a sé stesso, ma è soggetto a un lento moto conico di precessione e a oscillazioni, di minore entità, intorno alle generatrici del cono di precessione (nutazione), si riscontrano, in conseguenza, analoghe, piccole variazioni delle c. e un continuo, piccolo spostamento dei poli sulla superficie terrestre (migrazione dei poli). A queste variazioni, che si possono chiamare variazioni polari, se ne aggiungono altre, di entità ancora minore, e collegate non con moti dell’asse terrestre ma con variazioni della verticale locale, imputabili a varie cause. Il rilievo delle variazioni delle c., di estremo interesse non solo per la geodesia, ma anche per l’astronomia e per la geofisica, è effettuato con telescopi zenitali e cannocchiali meridiani estremamente precisi (si tratta di apprezzare differenze angolari dell’ordine di pochi decimi di secondo), ed è coordinato da appositi enti internazionali (Bureau des longitudes; Bureau international de l’heure; Ufficio centrale delle latitudini).

C. geomagnetiche

Sistema di c. al quale per comodità vengono riferiti i punti della superficie terrestre nella trattazione di alcuni problemi inerenti al magnetismo terrestre. Si tratta di un sistema del tutto analogo al sistema delle c. geografiche, salvo il fatto che gli elementi di riferimento sono, stavolta, l’equatore geomagnetico per le latitudini e, per le longitudini, il meridiano geografico passante per il polo geomagnetico Nord. Poiché gli elementi di riferimento sono soggetti a variare nel tempo, le c. geomagnetiche hanno senso se si precisa la posizione degli elementi stessi (per es., si precisano le c. geografiche del polo Nord geomagnetico) o, il che è lo stesso, l’epoca alla quale ci si riferisce.

Matematica

C. di un punto sulla retta

Su una retta r si fissi un punto O (origine), e uno dei due versi di percorrenza come verso positivo (usualmente da sinistra a destra se la retta si suppone orizzontale sul foglio). Si fissi inoltre un segmento di lunghezza u come unità di misura. Si dirà allora che si è fissato un sistema di riferimento sulla r. Allora: a) ad ogni punto P sulla retta corrisponde uno e un solo numero reale (ascissa di P), e cioè la misura con segno del segmento OP, rispetto all’unità di misura; b) viceversa a un numero reale corrisponde uno e un sol punto della retta. Con procedimento concettualmente analogo si può introdurre anche sopra una curva un’ascissa curvilinea.

C. di un punto nel piano

5A e 5B

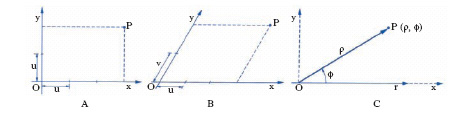
C. cartesiane. - Prendono il nome da Cartesio che per primo le introdusse e le utilizzò sistematicamente. Si fissino comunque nel piano (fig. 5A e 5B) un punto O (origine) e per esso due rette orientate Ox, Oy (assi coordinati cartesiani, rispettivamente asse delle x e asse delle y). Scegliendo inoltre su ciascun asse un’unità di misura, resta determinato su ciascuno di essi un sistema di ascisse di origine O. Si dirà così di avere fissato un sistema di riferimento. Si ha allora che: a) a ogni punto P del piano si può far corrispondere una coppia ordinata (x, y) di numeri reali: il primo di essi (ascissa di P) è l’ascissa, sull’asse delle x, del punto di intersezione di detto asse con la parallela per P all’asse delle y; il secondo (ordinata di P) è l’ascissa, sull’asse delle y, del punto d’incontro di detto asse con la parallela per P all’asse delle x; b) viceversa, a ogni coppia ordinata di numeri reali (x, y) corrisponde uno e un solo punto P del piano. In conclusione, fissato nel piano un sistema di riferimento cartesiano, si riesce a stabilire una corrispondenza biunivoca tra i punti del piano e le coppie ordinate di numeri reali (c. cartesiane). Si scriverà P (x, y), per indicare che l’ascissa di P è x, l’ordinata y. Il sistema di riferimento potrà essere: a) ortogonale od obliquo, a seconda che i due assi coordinati siano o no tra di loro ortogonali; b) monometrico o dimetrico a seconda che si sia scelta o no la medesima unità di misura per i due assi. Generalmente, si usano sistemi di riferimento ortogonali e monometrici. In tal caso, le c. di un punto non sono altro che le sue distanze (con segno) da due rette fisse, orientate, tra di loro ortogonali (gli assi anzidetti).

C. polari. - Presi nel piano (fig. 5C) un punto O (polo), e una retta orientata r (asse polare) passante per O, e fissati un verso positivo per le rotazioni (di solito quello antiorario) e un’unità per le lunghezze, restano individuati per ogni punto P del piano (distinto da O) il valore assoluto ρ della distanza OP (raggio vettore) e la misura (in radianti) ϕ dell’angolo, compreso tra 0 e 2π, che va dall’asse polare alla retta OP, orientata da O verso P (anomalia). Viceversa, dati questi due numeri, resta individuato P; ρ e ϕ si chiameranno allora le c. polari di P e si scriverà: P (ρ, ϕ). Le relazioni tra le c. cartesiane e polari di un punto in un piano, quando si scelga l’asse x come asse polare e l’origine come polo, sono:

C. di un punto nello spazio

fig. 6A

C. cartesiane (fig. 6A). - Si fissino nello spazio tre rette Ox, Oy, Oz, spigoli di un triedro, e su ciascuna di queste un verso come positivo e una unità di misura, in modo che resti determinato su ciascuna delle tre rette un sistema di ascisse, avente O come origine. Preso allora nello spazio un qualsiasi punto P, si conducano per esso i tre piani paralleli alle facce Oyz, Ozx, Oxy del triedro considerato; essi incontreranno gli spigoli Ox, Oy, Oz rispettivamente nei tre punti P1, P2, P3: le ascisse di questi tre punti, nell’ordine detto, sono le c. cartesiane del punto P. Analogamente a quanto accade nel piano, si stabilisce così una corrispondenza biunivoca tra punti dello spazio e terne ordinate di numeri reali. Se la terna scelta è trirettangola, e l’unità di misura è comune ai tre assi, le tre c. cartesiane (chiamate, nell’ordine, ascissa, ordinata e quota) di P rappresentano le distanze di P (con segno) da tre piani fissi mutuamente ortogonali. I tre piani determinati dalle tre coppie di assi si chiamano piani coordinati. La terna di assi x, y, z è di solito una terna levogira, ma può trattarsi indifferentemente anche di una terna destrogira.

C. polari (fig. 6B). - Presi nello spazio un punto O (polo), una retta orientata r per O (asse polare), un semipiano a uscente da r (semipiano polare), e infine un verso positivo nel fascio di piani di asse r, ogni punto P dello spazio può venire individuato mediante i seguenti tre numeri: a) la sua distanza ρ (positiva o nulla) dal polo O, detta raggio vettore di P; b) l’angolo ϑ, compreso tra 0 e π, delle due rette orientate r e OP, detto colatitudine (o distanza zenitale); c) l’angolo ϕ, compreso tra 0 e 2π, dei due semipiani a e Pr, detto longitudine (o azimut). Tali c. sono spesso chiamate anche c. sferiche, poiché le c. ϑ e ϕ si possono anche considerare come c. curvilinee sopra una sfera di raggio ρ. Le formule che permettono il passaggio dalle c. polari (ρ, ϑ, ϕ) alle c. cartesiane ortogonali (x, y, z) di uno stesso punto P (quando r coincide con l’asse z, O con l’origine, α con il piano xz) sono:

.

C. cilindriche (o semipolari). - Un punto P dello spazio, le cui c. cartesiane ortogonali siano (x, y, z) può anche venire individuato dalla sua quota z e dalle c. polari ρ, ϕ della sua proiezione sul piano x y (piano equatoriale); ρ, ϕ, z sono le c. cilindriche di P.

C. generali curvilinee

Si considerino nel piano due sistemi ∞¹ di curve, due sistemi cioè dipendenti ciascuno da un parametro arbitrario (u per il primo e v per il secondo). Supponiamo che, almeno in una certa regione R del piano, per ogni punto P passi una e una sola curva di ciascun sistema, in modo inoltre che ogni curva di un sistema incontri in un sol punto ogni curva dell’altro sistema (in tal caso si parla anche di «sistema doppio di curve»). Allora a ogni punto P della regione R restano associati due valori u, v (quelli relativi alle curve passanti per esso), che si dicono c. curvilinee o generali del punto P, naturalmente rispetto ai due fissati sistemi di curve. Le curve stesse prendono il nome di curve o linee coordinate, e stabiliscono appunto nella regione R un sistema di c. curvilinee. Si noti che in tutti i punti di una linea coordinata risulta costante una delle due c. curvilinee u o v, per cui si parla anche di linee u = cost, o v = cost (rispettivamente per i due sistemi di linee) o anche, di linee v e di linee u. Un sistema di c. curvilinee si dice poi doppiamente ortogonale se una qualunque linea u interseca ad angolo retto una qualunque linea v. Tra le c. curvilinee nel piano rientrano come casi particolari le c. cartesiane ortogonali, per cui le linee u e v sono le parallele ai due assi coordinati; le c. polari, per cui le linee u e v sono le semirette per il polo O e le circonferenze di centro O (in entrambi i casi si tratta di sistemi doppiamente ortogonali). Un altro esempio notevole è offerto dalle c. ellittiche, usate per es. in meccanica razionale per lo studio dell’attrazione di un punto da due centri fissi; in esse, le linee coordinate sono rispettivamente un sistema di ellissi, e un sistema di iperboli, tutte aventi gli stessi fuochi.

Le considerazioni qui svolte nel caso del piano si possono estendere allo scopo di introdurre due c. curvilinee sopra una superficie qualunque sempre mediante un sistema doppio di curve, ovvero per introdurre tre c. curvilinee nello spazio a tre dimensioni mediante un sistema triplo di superfici, a seconda dei sistemi di curve o superfici che vengono scelti si ottengono tipi differenti di c. curvilinee: le c. sferiche, ellissoidiche, toroidali ecc.; un interessante esempio di c. curvilinee sopra una sfera è dato dalle c. celesti.

C. omogenee

C. definite a meno di un fattore di proporzionalità. Per es., nel piano si possono introdurre le due c. cartesiane x, y, di un punto che sono univocamente determinate dal punto stesso; ma possono anche introdursi tre c. omogenee x₁, x₂, x₃ (legate alle precedenti dalle relazioni x = x₁/x₃, y = x₂/x₃), nel qual caso a un punto resta associata una terna di numeri e tutte quelle a essa proporzionali per un fattore non nullo. Sono le c. più adatte per lo studio delle proprietà proiettive delle figure.

Strumentazione

Coordinatografo Strumento impiegato per riportare su una planimetria o su un grafico un punto di cui siano note le c., costituito da un dispositivo di riferimento e da una punta scrivente. Nel coordinatografo ortogonale il sistema di riferimento è formato da due regoli graduati, perpendicolari fra loro, su cui si leggono le c. del punto; nel coordinatografo polare vi è invece un cerchio graduato nel cui centro è imperniata un’asta anch’essa graduata. La valutazione delle c. si esegue manualmente o automaticamente nei modelli di precisione. Un coordinatografo automatico connesso con un calcolatore elettronico consente di tracciare disegni, mappe o figure, anche di notevole complessità, con grande precisione in modo automatizzato. Coordinatometro Strumento impiegato per la valutazione di c., cartesiane o polari, su carte o grafici. È analogo al coordinatografo, ma alla punta scrivente si sostituisce un dispositivo di puntamento spesso dotato di un reticolo di riferimento. Può essere reso automatico mediante scansione magnetica di un reticolo formato da fili metallici su cui si sovrappone la carta o il grafico da esaminare.