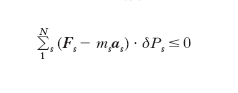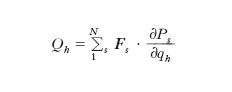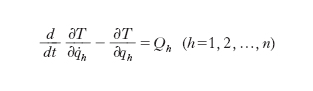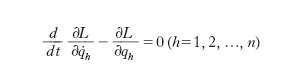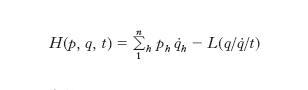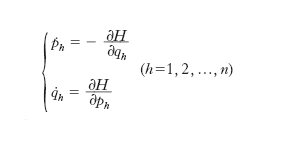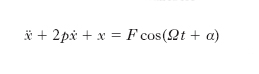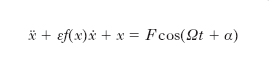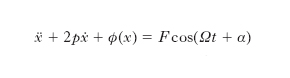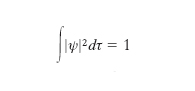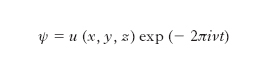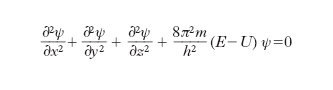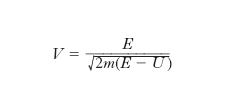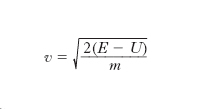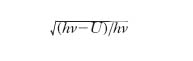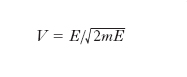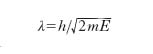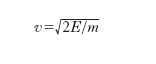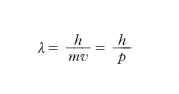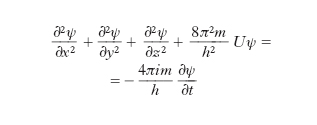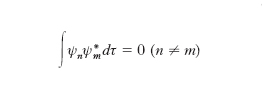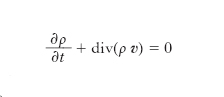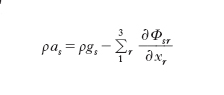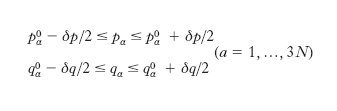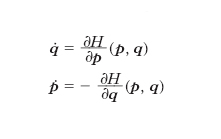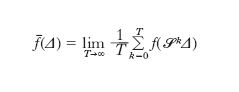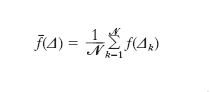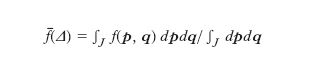meccanica

Scienza che studia il moto e l’equilibrio dei corpi. È tradizionalmente divisa in tre parti: cinematica, dinamica e statica, che studiano, rispettivamente, il moto prescindendo dalle sue cause, il moto in relazione alle cause che lo determinano e l’equilibrio dei corpi.

Storia della meccanica

La nascita della meccanica I primi scritti in cui sono trattati, nell’antichità classica, problemi meccanici (di statica e di dinamica) sono la Fisica e Il cielo di Aristotele e le Questioni meccaniche attribuito sempre ad Aristotele. Mentre la statica aristotelica poggia su fondamenti generalmente accettabili, la sua dinamica è basata sul principio, rimasto in vigore attraverso l’opera dei commentatori sino ai tempi di Galileo, che non può esservi movimento in assenza di una forza motrice. Ad Archimede sono dovute le prime ricerche teoriche sui baricentri, una teoria dell’equilibrio della leva (in cui si ritrova, embrionalmente, il moderno principio dei lavori virtuali), la legge di idrostatica che porta il suo nome.

I contributi dei filosofi greci pervennero in Occidente, tramite gli Arabi e i commentatori di Aristotele, pressoché inalterati, e vi subirono notevoli rielaborazioni, a opera specialmente della scuola parigina del 14° secolo. Accanto all’isolata (e pressoché sconosciuta ai suoi contemporanei) opera di Leonardo fiorisce, fra il Quattrocento e il Cinquecento, una varietà di ricerche e di studi, dovuta a filosofi e matematici; tuttavia la nascita della nuova m. è segnata dalla riforma astronomica di N. Copernico, compiuta poi da J. Kepler, che fissa le leggi del moto dei pianeti.

La costruzione delle basi della nuova scienza si accentra intorno ai tre grandi nomi di G. Galilei, di ^{C. Huygens}, e di I. Newton. Galilei afferma per primo chiaramente il concetto che le circostanze determinatrici del moto individuano l’accelerazione e dà di questa una nozione precisa; con la formulazione delle leggi del moto dei gravi nel vuoto, stabilisce in sostanza la dinamica del punto materiale soggetto a forza costante; enuncia il principio di relatività (ora detta galileiana); formula in modo netto, se pur limitatamente a un caso particolare, la legge d’inerzia; scopre la legge dell’isocronismo del pendolo ecc. Le scoperte di Galilei e l’opera scientifica e filosofica di Descartes costituiscono la base su cui si sviluppa l’opera di Huygens, cui si devono tra l’altro le nozioni di momento d’inerzia e di forza centrifuga, la dinamica del pendolo composto, talune idee precorritrici sulla conservazione dell’energia. La conservazione della quantità di moto di un sistema isolato era stata invece affermata da Descartes. Le idee e i risultati conseguiti trovano in Newton la sintesi: egli fissa il concetto di massa; generalizza quello di forza; enuncia, in tutta la loro generalità, le tre leggi fondamentali (principio d’inerzia, relazione tra forza e accelerazione, principio di azione e reazione); formula la legge della gravitazione universale, cardine della m. celeste.

Sulla base dei principi newtoniani, qualunque problema meccanico può essere matematicamente impostato, ma la sua effettiva risoluzione richiede l’impiego di appropriati strumenti matematici: i concetti e i metodi dell’analisi infinitesimale ebbero in Newton stesso e in G.W. Leibniz i suoi creatori; la m. finisce sostanzialmente di essere sperimentale e diventa razionale.

La meccanica dal 18° secolo In questo secolo i progressi sono in gran parte legati, in ogni ramo della m., al perfezionarsi dello strumento analitico. Giacomo, Giovanni e Daniele Bernoulli stabiliscono nella sua generalità il teorema delle forze vive, mentre D. Bernoulli e L. Euler fondano la dinamica dei fluidi perfetti e danno, indipendentemente l’uno dall’altro, il teorema del momento delle quantità di moto che viene ad affiancarsi, come secondo cardine della dinamica dei sistemi, al teorema delle quantità di moto già stabilito da Newton. J.-B. d’Alembert enuncia il principio che va oggi sotto il suo nome e che con il principio dei lavori virtuali, modernamente formulato da G. Bernoulli, costituisce il fondamento primo della cosiddetta meccanica analitica. Questa, iniziatasi con Euler, si sviluppa sul finire del Settecento e all’inizio dell’Ottocento, prevalentemente a opera di G.L. Lagrange e di W.R. Hamilton. Connesso per molti aspetti agli sviluppi della m. analitica è il progresso della meccanica celeste, che trova in P.-S. Laplace e poi in J.-H. Poincaré approfondimenti e sviluppi di fondamentale rilievo.

Fecondo di risultati è il 19° sec., in cui singoli rami e particolari questioni della m. sono oggetto di studio: in particolare nella m. dei sistemi continui A.-L. Cauchy fissa alcuni teoremi generali destinati a costituire il fondamento della teoria; d’Alembert, Lagrange, H. Helmholtz, G.R. Kirchhoff, lord W.T. Kelvin portano nuovi ed essenziali contributi alla m. dei fluidi perfetti; S.-D. Poisson, G.G. Stokes, J.W.S. Rayleigh, O. Reynolds sviluppano la m. dei fluidi viscosi nata dalle esperienze di C.-A. Coulomb; L.-M.-H. Navier, G. Lamé, A. de Saint-Venant, R.F. Clebsch pongono le basi della m. dei sistemi elastici dando vita alla teoria matematica dell’elasticità. Sempre nel 19° sec. nasce, a opera di J.C. Maxwell, J.W. Gibbs e L. Boltzmann, un nuovo ramo della m., la cosiddetta meccanica statistica.

Due fatti di portata veramente rivoluzionaria si producono all’alba del 20° sec.: da un lato l’introduzione dei principi relativistici, in contrapposto a quelli classici di Galilei e di Newton, dall’altro l’avvento della concezione quantistica, discontinua, dell’energia. I postulati fondamentali della relatività, affermati (1905) da A. Einstein, e accolti inizialmente non senza contrasti e perplessità, si radicarono nel fertile terreno preparato dalla revisione dei principi e dei concetti classici operata da H. Hertz, E. Mach e Poincaré, nonché dalla insostenibilità di talune ipotesi (come quella dell’etere cosmico): la meccanica relativistica che ne è nata non soppianta peraltro la m. classica ma la contiene nel caso limite dei cosiddetti fenomeni lenti, caratterizzati da velocità molto minori della velocità della luce nel vuoto. La necessità di introdurre nella m. atomica un elemento di discontinuità, che non appare nelle leggi che governano i corpi di dimensioni ordinarie, fu riconosciuta per la prima volta nel 1900 da M. Planck. L’indirizzo inaugurato da Planck ha avuto sviluppi della più grande importanza per la conoscenza delle leggi che governano il microcosmo; tali sviluppi sono ormai sistematicamente organizzati nella meccanica quantistica, a opera principalmente di W. Heisenberg, di E. Schrödinger e di P.A.M. Dirac. La m. quantistica contiene come caso limite la m. classica (principio di corrispondenza).

Le varie branche della meccanica Comune fondamento delle varie branche in cui si è sviluppata la m. come scienza è quel corpo di dottrine tradizionalmente noto con il nome di meccanica razionale. La locuzione può indicare qualunque parte della m. che si sviluppi con procedimento matematico deduttivo da alcuni principi generali. Peraltro il termine è da considerarsi piuttosto come sinonimo di meccanica classica macroscopica, cioè di quella parte della m. che, sulla base dei postulati newtoniani (➔ dinamica), studia problemi meccanici relativi a corpi di dimensioni ordinarie, nei vari schemi adottati a rappresentarli, prescindendo da eventuali altri fenomeni concomitanti al fatto meccanico vero e proprio (quali, per es., i fenomeni chimici, elettrici, termici ecc.).

Meccanica analitica

La m. analitica, come la m. razionale, ha principalmente per oggetto la deduzione, da alcuni principi di amplissima validità, delle leggi del moto sotto assegnate sollecitazioni; i sistemi che essa prende in considerazione sono di tipo più generale e complesso di quelli presi in esame dalla m. razionale propriamente detta, e sono così più generali e complessi i metodi analitici di cui si serve. Fra tali sistemi hanno particolare rilievo i sistemi olonomi, le cui configurazioni possono, a ogni istante, esser poste in corrispondenza biunivoca con un certo numero finito, n, di parametri arbitrari, fra loro indipendenti (gradi di libertà o coordinate lagrangiane) e i cui eventuali vincoli sono tutti olonomi (cioè implicano, direttamente, soltanto limitazioni alle posizioni e non all’atto di moto).

La m. analitica si fonda sul principio di d’Alembert e sul principio dei lavori virtuali. Per quanto riguarda il primo, si immagini di avere un sistema costituito da N punti e siano m_s la massa del generico punto P_s, F_s la forza attiva a esso applicata, δP_s un qualunque spostamento virtuale di P_s all’istante in esame; a causa dei vincoli l’accelerazione a_s del punto non è data dal rapporto F_s/m_s, ossia il prodotto m_sa_s è diverso da F_s, e (F_s−m_sa_s) rappresenta la ‘forza perduta’: il principio di d’Alembert esprime il fatto che a ogni istante durante il moto del sistema le ‘forze perdute’ e le ‘forze vincolari’ si equilibrano a vicenda. Il principio dei lavori virtuali afferma poi che il lavoro virtuale delle forze vincolari offerte da vincoli privi di attrito non può mai essere negativo (➔ lavoro). L’intervento di tale principio come base della m. analitica subordina gli sviluppi essenziali di questa teoria all’ipotesi che non entrino in gioco sensibili attriti. La combinazione dei due principi porta a stabilire la relazione simbolica della dinamica o relazione di d’Alembert e Lagrange:

[1] formula

Se il sistema in esame è un sistema olonomo soggetto a vincoli tutti bilaterali, in modo tale che nella [1] valga il segno di uguaglianza, la [1] medesima dà luogo alle equazioni di Lagrange. Il sistema abbia n gradi di libertà e sia q₁, q₂, ..., q_n una n-pla di coordinate lagrangiane opportunamente scelte. Se il sistema è in moto, le q sono naturalmente da considerarsi come funzioni del tempo a priori incognite; ma il fatto che esse siano atte a individuare le configurazioni del sistema equivale a dire che la posizione del generico punto di questo può essere a priori espressa in funzione delle q medesime (e del tempo se i vincoli sono mobili):

P_s = P_s (q₁, ..., q_n; t).

In conseguenza di ciò sono subito esprimibili in funzione, in generale, sia delle q sia delle loro derivate q̇ rispetto al tempo, sia di t medesimo, tanto l’energia cinetica T del sistema, che risulta una funzione quadratica delle q̇, quanto le cosiddette componenti lagrangiane,

,

della sollecitazione attiva. Queste grandezze, come si dimostra a partire dalla [1], risultano legate dalle relazioni

[2] formula

che sono appunto le equazioni di Lagrange o, con più precisa denominazione, la ‘seconda forma delle equazioni di Lagrange’. Si tratta di un sistema di n equazioni differenziali del second’ordine nelle n funzioni incognite q₁(t), q₂(t), ..., q_n(t), quindi di un sistema atto a determinare completamente il moto quando siano altresì assegnati i valori iniziali delle q e delle q̇. Semplice ed estremamente sintetica è la sua struttura: la sollecitazione attiva è raccolta nelle componenti lagrangiane Q_h, le proprietà materiali del sistema nell’espressione T dell’energia cinetica. È notevole il fatto che il moto di sistemi, anche apparentemente molto diversi, ma con la stessa espressione per T e per le Q_h, sia retto dalle stesse equazioni di Lagrange: è il caso dei cosiddetti sistemi dinamicamente equivalenti. Nel caso particolarmente importante in cui la sollecitazione attiva sia conservativa, ove se ne denoti con U=U(q₁,...,q_n) il potenziale, risulta Q_h=∂U/∂q_h, e indicando con L la somma dell’energia cinetica e del potenziale, L=T+U, le [2] possono essere poste nella forma

[3] formula.

La funzione L(q, q̇, t) è detta funzione di Lagrange o lagrangiana; per un sistema soggetto a sollecitazione conservativa essa riassume tutte le proprietà del sistema e della sollecitazione. Le quantità a primo membro delle [3] sono ricordate come binomi lagrangiani; le quantità p_h=∂L/∂q̇_h come momenti cinetici. Generalizzando, ogni sistema differenziale che abbia la struttura del sistema [3], quale che sia il significato della L, si chiama ancora sistema lagrangiano.

Un sistema lagrangiano [3] può trasformarsi, in infiniti modi, in un sistema di 2n equazioni differenziali del primo ordine in 2n funzioni incognite del tempo. Una tra le più notevoli di tali trasformazioni, detta trasformazione di Hamilton, è la seguente. Si assumono come incognite, accanto alle n coordinate lagrangiane q, gli n momenti cinetici (variabili coniugate delle q) legati alle q̇ dalle relazioni p_h=∂L/∂q̇_h che, risolte rispetto alle q̇, danno q̇_h=u_h (p/q/t). Introdotta allora la funzione (funzione di Hamilton o hamiltoniana):

[4] formula,

dove ciascuna delle q̇ s’intenda espressa, come detto, in funzione delle p, delle q e di t, il sistema [3] si trasforma nel sistema hamiltoniano o canonico

[5] formula,

costituito appunto da 2n equazioni differenziali del primo ordine, dette canoniche, nelle 2n funzioni incognite p_h, q_h (variabili canoniche). È particolarmente notevole il significato fisico dell’hamiltoniana nel caso meccanico se i vincoli non dipendono dal tempo; in questo caso il potenziale U (o l’energia potenziale −U) dipende solo dalle q_h, cioè U=U (q_h), per cui i momenti cinetici p_h sono anche uguali a ∂T/∂q̇_h (in quanto L=T+U). Il primo termine del secondo membro della [4], per il fatto che T è una funzione omogenea quadratica delle q̇_h, è uguale a 2T; di conseguenza risulta H=T−U: cioè, H, somma dell’energia cinetica e di quella potenziale, rappresenta l’energia totale del sistema. Sempre per vincoli fissi, se H non dipende esplicitamente dal tempo, sussiste l’integrale dell’energia (o delle forze vive): H(p, q)=cost. Il medesimo integrale sussiste anche se i vincoli non sono fissi ma resta valida l’ipotesi che H non dipenda esplicitamente dal tempo: la relazione H(p, q)=cost. ha allora il nome di integrale generalizzato dell’energia. Gli stessi fatti si verificano se, anziché H, è L indipendente dal tempo.

Meccanica applicata

Complesso delle discipline in cui trovano applicazione i principi e i metodi della m. razionale. È possibile distinguere la m. applicata in m. applicata alle costruzioni, m. applicata ai fluidi e m. applicata alle macchine. La meccanica applicata alle costruzioni ha per oggetto le applicazioni pratiche dei principi della m. e della teoria dell’elasticità allo studio statico e dinamico delle strutture ed è assai più comunemente nota come scienza delle costruzioni. La meccanica applicata ai fluidi, detta più frequentemente fluidodinamica, studia il moto dei fluidi e dei corpi in essi immersi, ed è a sua volta distinta in idrodinamica, aerodinamica, gasdinamica, magneto-fluidodinamica. La m. applicata alle costruzioni e la m. applicata ai fluidi possono, come impostazione, fare capo alla m. dei sistemi continui. La meccanica applicata alle macchine concerne invece gli elementi delle macchine, sia riguardo alla loro capacità di trasmettere moto sia riguardo a quello di trasmettere forze. Se lo studio è limitato all’individuazione del moto consentito ai diversi organi delle macchine in conseguenza dei vincoli, sia esterni che interni, tale studio è essenzialmente cinematico.

Meccanica celeste

Parte dell’astronomia teorica che considera i movimenti dei corpi celesti in relazione alle forze che li producono e alle leggi che li governano. Generalmente, la m. celeste in senso proprio si occupa soltanto dei corpi del sistema solare, cioè pianeti, satelliti, pianetini e comete, ed è questa la parte classica, sorta a opera di matematici e astronomi del 17°, 18° e 19° sec. dopo la scoperta della legge di Newton. Il successivo estendersi delle conoscenze astronomiche ai sistemi stellari e a tutto l’universo sidereo ha fatto estendere e completare, nel 20° sec., le ricerche della m. celeste classica con l’introduzione anche di nuovi metodi e nuovi ausili di calcolo. Ma questa nuova parte si è ben presto distaccata dall’antica, prendendo piuttosto i nomi di dinamica stellare e di statistica stellare, mentre la denominazione di m. celeste è rimasta alla m. del sistema planetario.

La m. celeste si basa sull’equazione fondamentale della dinamica, F=ma, dove m è la massa, a l’accelerazione di un corpo celeste e F la forza che su esso agisce, derivante dalla legge della gravitazione universale. Nell’ipotesi che ogni pianeta sia sottoposto alla sola azione del Sole, la soluzione dell’equazione del moto permette di determinare l’orbita del pianeta, per la quale vengono dedotte le leggi di Keplero (➔ Kepler, Johannes), che, ottenute originariamente mediante la pura osservazione, si trovano così a essere giustificate teoricamente. Ma l’azione del Sole, se pur preponderante, non è la sola forza che sollecita i corpi del sistema planetario; essi subiscono anche le rispettive mutue attrazioni. Queste seconde forze, dette perturbazioni planetarie, sono molto piccole ma bastano tuttavia a spiegare le irregolarità che alterano i moti dei pianeti e che impediscono loro di soddisfare rigorosamente alle leggi di Keplero.

Risale a Eulero il merito di aver calcolato per primo queste irregolarità dei moti planetari. Alla fine del 18° sec. e al principio del 19° sec. la fondamentale opera di Laplace e di Lagrange segna sostanzialmente la sistemazione definitiva della m. celeste. La Mécanique céleste di Laplace ha profondamente influito su tutta la numerosa schiera dei suoi continuatori, tra cui Poisson, U.-J.-J. Le Verrier, C.-E. Delaunay, J.-C.-R. Radau, F.-F. Tisserand, P.-J.-O. Callandreau, Poincaré. Nessuno di questi insigni matematici e astronomi si è mai occupato di osservazioni celesti: quando Le Verrier volle confermare in cielo la scoperta di Nettuno ricorse a J.G. Galle, che, a Berlino, riuscì a osservare l’astro. L’opera di Poincaré, in particolare, ha segnato una svolta nella m. celeste, con l’introduzione di nuovi metodi e con il conseguimento di nuovi risultati, ai quali si sono improntate tutte le ricerche successive fino ai nostri giorni.

Meccanica non lineare

Parte della fisica-matematica che studia i fenomeni oscillatori (di natura meccanica, elettrica ecc.), la cui teoria può svolgersi soltanto mediante equazioni differenziali non lineari. Ricordiamo, come esempio semplice di sistema meccanico che compie oscillazioni libere, un punto P, mobile su una retta, soggetto a una forza elastica proporzionale e opposta all’ascissa x di P e a una forza resistente −2pẋ proporzionale e opposta alla velocità ẋ di P. Il punto P compie invece oscillazioni forzate, se alle precedenti si aggiunge un’altra forza, per es. del tipo F cos(Ωt+α), cioè funzione sinusoidale del tempo t. Le grandezze p, F, Ω, α sono costanti. Scegliendo le unità di misura in modo che risultino unitari la massa di P e il coefficiente elastico, la x(t) verifica l’equazione differenziale lineare

[6] formula,

cui possono ricondursi numerosi altri sistemi meccanici o elettrici, sostituendo la costante 2p con una funzione εf (x) della x (e, in qualche caso, anche della ẋ):

[7] formula

dove ε è una costante maggiore di zero; è questa l’equazione differenziale di Liénard, non lineare per la presenza del termine f(x)ẋ, con F=0 nel caso delle oscillazioni libere, con F≠0 nel caso delle oscillazioni forzate. Altri problemi si riconducono all’equazione differenziale non lineare

[8] formula

ottenuta dalla [6] sostituendo alla forza elastica una forza −ϕ (x) funzione generica della x. La [7], eventualmente generalizzata ponendovi f(x, ẋ) o anche f(x, ẋ, t) in luogo di f(x)ẋ, e la [8] sono le più importanti equazioni differenziali della m. non lineare relativa a sistemi con un solo grado di libertà. Questi sistemi si dicono autonomi se, nelle equazioni che li governano, non compare esplicitamente il tempo: per es., se nella [7], con f(x)ẋ eventualmente sostituito da f(x,ẋ), è F=0; non autonomi nel caso opposto: per es. se nella [7] è F≠0, oppure compare un termine f(x, ẋ, t). Lo studio quantitativo delle [7], [8] e delle loro generalizzate può farsi con vari meto;di approssimati (Poincaré, B. Van der Pol, N. Krylov e N. Bogoljubov, N. Minorsky ecc.), validi per debole non linearità, cioè per ε≪1, e quando ϕ(x) differisca di abbastanza poco da x. Lo studio qualitativo (esistenza di soluzioni periodiche, unicità, stabilità ecc.) si fa invece, di solito, riconducendo le [7], [8] e le loro ge;neralizzate a sistemi differenziali del primo ordine e valendosi poi di considerazioni topologiche: come, per es., nella teoria di Poincaré per i sistemi di equazioni differenziali del primo ordine, utilissima nel caso particolare dei sistemi autonomi.

Ha notevole importanza il caso in cui, nella [7], f(x) è negativa in un intorno dell’origine (cioè per piccoli valori di ∣x∣), positiva per x esterno a quest’intorno: tale è, per es., il caso f(x)=x²−1, in cui la [7] si riduce alla classica equazione di Van der Pol. Ovviamente, quando f(x) è negativa, il lavoro della forza −εf(x)ẋ è positivo (ε essendo >0), cioè viene immessa dall’esterno energia nel sistema: si comprende, perciò, come esso possa compiere oscillazioni libere senza smorzamento. Facendo qualche altra ipotesi qualitativa sulla f(x), si perviene, quando è F=0, ai seguenti risultati: a) la posizione di equilibrio del sistema (soluzione x ≡ 0 della [7]) è instabile e pertanto non è assunta, in pratica, dal sistema; b) le altre soluzioni di [7] sono sempre oscillatorie intorno all’origine (a differenza del caso lineare [6], nel quale sono tali soltanto se è p <1) e tendono asintoticamente a un’unica soluzione periodica stabile. In altre parole, il sistema retto dalla [7] compie, praticamente, dopo un intervallo di tempo transitorio, oscillazioni periodiche. Va rilevato però che, a differenza del caso lineare, tali oscillazioni non dipendono dalle condizioni iniziali. Nel piano (x, ẋ) detta soluzione periodica è rappresentata da una curva chiusa C (ciclo limite stabile, secondo Poincaré), che circonda l’origine e alla quale tendono tutte le altre curve che rappresentano soluzioni di [7] con F=0. Se ε ≪1, la soluzione periodica è sensibilmente sinusoidale, con periodo prossimo a 2π; l’ampiezza, nel caso di Van der Pol, vale 2. Se è invece ε ≫1, come è stato riconosciuto dallo stesso Van der Pol, la soluzione periodica dell’equazione (di tipo [7]) ha periodo 1,614 ε e si identifica con l’ascissa x di un punto P che si muova percorrendo due segmenti MN, M′N′, simmetrici rispetto all’origine O (OM>ON, O esterno a MN), nel seguente modo: partito da M, il punto P percorre MN; giunto in N ‘salta’ bruscamente in M′; quindi percorre M′N′, salta in M; e così di seguito. Le oscillazioni di questo tipo, che sono, in sostanza, una successione periodica di fenomeni aperiodici, si dicono ‘di rilassamento’ e si osservano in molti fenomeni fisici: tale è, per es., l’andamento della corrente assorbita da una lampada a neon convenientemente alimentata (➔ oscillatore).

Meccanica quantistica

Meccanica quantistica e meccanica ondulatoria Può essere definita come la m. dei sistemi (elettroni, nuclei, atomi, molecole ecc.) di dimensioni estremamente piccole rispetto alle dimensioni dei corpi ordinari, i quali non ubbidiscono alle leggi della m. e dell’elettromagnetismo valide per i corpi e i sistemi ordinari. La m. quantistica è sorta quasi contemporaneamente sotto due forme in apparenza molto diverse: la teoria delle matrici, detta anche, fin da principio, meccanica quantistica (Quantenmechanik) di W. Heisenberg (1925), e la meccanica ondulatoria, della quale la prima idea è dovuta a L. de Broglie (1924) mentre i successivi sviluppi sistematici sono dovuti principalmente a E. Schrödinger (1926). Lo stesso Schrödinger ha dimostrato che le due teorie sono equivalenti, cioè esse non sono in definitiva che due forme matematiche diverse di una stessa teoria. Evitando ipotesi artificiose che le precedenti teorie quantistiche non avevano potuto evitare, la m. quantistica ha consentito una più soddisfacente interpretazione di vari risultati sperimentali; fra questi va ricordato in primo luogo il fenomeno della diffrazione degli elettroni (Davisson e Germer, 1927) che, inesplicabile nell’ambito delle vecchie teorie quantistiche, è invece previsto e perfettamente inquadrato, anche sotto l’aspetto quantitativo, dalla m. ondulatoria. Successivamente la m. quantistica ha assunto una forma nuova e più generale, nella quale rientrano come casi particolari la teoria delle matrici e la m. ondulatoria, con la cosiddetta teoria delle trasformazioni, dovuta a P.A.M. Dirac e P. Jordan e basata su convenienti utilizzazioni del metodo matematico degli operatori; mentre altri potenti strumenti d’indagine hanno fornito la sistematica introduzione, a opera di H. Weil, dei metodi matematici della teoria dei gruppi.

Le origini della meccanica ondulatoria Punto di partenza per comprendere le origini della m. ondulatoria è stata la considerazione di taluni aspetti contraddittori in alcuni fenomeni luminosi. Infatti mentre alcuni di questi fenomeni (come l’interferenza) si spiegano bene considerando la luce come un fenomeno ondulatorio e sembrano incompatibili con ogni teoria corpuscolare, altri invece (come l’effetto fotoelettronico) si spiegano se si ammette la natura corpuscolare della luce e riescono inesplicabili in base all’ipotesi della natura ondulatoria di essa. L’apparente contraddizione si risolve considerando che idee e operazioni, magari solo concettualmente possibili nella scala ordinaria, possono divenire, anche concettualmente, impossibili nell’ambito del microcosmo. In particolare, i fenomeni con cui ci si rivela una radiazione (di frequenza visibile o no) consistono sempre in modificazioni subite da elettroni, atomi, o molecole (della retina dell’occhio, della lastra fotografica, della cella fotoelettrica ecc.) in conseguenza di un assorbimento o di una perdita di energia.

L’energia si trasmette per quanti, i quali, in particolare i fotoni, non sono corpuscoli nel senso ordinario del termine e non si comportano come tali in ogni circostanza. I fotoni e i quanti in genere, ma anche le cosiddette particelle elementari (elettroni, protoni, neutroni ecc.), danno luogo a fenomeni di duplice aspetto, corpuscolare e ondulatorio, che solo a prima vista possono apparire in contraddizione poiché essi non si manifestano mai simultaneamente ma appaiono come due aspetti ‘complementari’ che si integrano a vicenda (principio di complementarità). Una discussione rigorosa dei fenomeni con cui si rivelano queste particelle ha mostrato infatti che, allo stesso modo che per i quanti, è impossibile attribuire a esse una certa posizione e insieme una certa velocità perché le esperienze, anche ideali, per determinare l’una sono incompatibili con quelle per determinare l’altra (➔ indeterminazione, principio di).

Un importante elemento di collegamento tra la teoria classica e la m. quantistica è dato dal cosiddetto principio di corrispondenza di N. Bohr che, nella sua più generale formulazione, asserisce che le leggi della m. quantistica assumono la stessa forma delle leggi della fisica classica quando entrano in gioco transizioni fra stati caratterizzati da numeri quantici aventi valori molto elevati e poco diversi fra loro.

Analogia fra le leggi dell’ottica geometrica e quelle della meccanica Punto di partenza di Schrödinger è stata la considerazione: fra le leggi dell’ottica geometrica e quelle della m. del punto vi è un’analogia, già indicata in modo matematicamente preciso da Hamilton, che può essere spinta anche all’aspetto quantitativo delle leggi. Le leggi dell’ottica geometrica cessano di essere valide quando entrano in gioco schermi, fessure ecc. di dimensioni relativamente piccole: in tal caso nascono gli svariati fenomeni della diffrazione, i quali provano che le leggi esatte dell’ottica sono di tipo ondulatorio e quelle dell’ottica geometrica ne rappresentano soltanto un’approssimazione valida per sistemi fisici sufficientemente grandi. Poiché l’esperienza ha dimostrato che le leggi della m. ordinaria non valgono più per i sistemi di dimensioni piccolissime, si è condotti a pensare, guidati dall’analogia con l’ottica, che anche le leggi meccaniche siano, a rigore, di natura ondulatoria, con lunghezze d’onda dell’ordine delle dimensioni atomiche, cosicché in tutti i sistemi di dimensioni ordinarie si può applicare l’approssimazione corrispondente all’ottica geometrica, cioè la m. classica, mentre ai sistemi di dimensioni atomiche si devono applicare leggi meccaniche nuove, analoghe a quelle dell’ottica ondulatoria. Quest’idea, suggerita da precedenti geniali intuizioni di de Broglie, è stata poi precisata e sviluppata da Schrödinger.

Analogamente a quanto fa l’ottica per i fotoni, la m. ondulatoria delle particelle si propone di ricercare la probabilità che la particella considerata si trovi in un dato istante in un elemento di volume dτ, e per il calcolo di questa probabilità introduce una funzione, in genere complessa, ψ (x, y, z, t), detta funzione d’onda o ampiezza di probabilità, il quadrato del cui modulo moltiplica;to per dτ, ∣ψ(x, y, z, t)∣²dτ, dà la probabilità che in una misura la particella in esame si trovi all’istante t in un intorno di volume dτ del punto di coordinate x, y, z. Per il fatto che la probabilità totale di presenza in tutto lo spazio deve essere 1, la ψ resta assoggettata alla condizione, detta di normalizzazione,

[9] formula,

dove l’integrale s’intende esteso a tutto lo spazio. Se E è l’energia totale della particella, ψ può essere posta nella forma

[10] formula

con ν=E/h; e, al pari della funzione puramente spaziale u, deve soddisfare l’equazione di Schrödinger:

[11] formula

dove U è l’energia potenziale del campo di forza che agisce sulla particella. La [11] rappresenta analiticamente la propagazione di onde (onde di de Broglie), con velocità di fase

e con velocità di gruppo

Se ψ è nulla dappertutto tranne che in una regione dello spazio abbastanza piccola da poterla considerare puntiforme, in modo da avere un pacchetto d’onde, questa regione, che in tal caso rappresenta la posizione approssimata della particella, si muove secondo le leggi dell’ordinaria m. del punto. Così la m. ondulatoria si ricollega con continuità alla m. ordinaria. L’equazione di Schrödinger è analoga all’equazione delle onde elettromagnetiche di frequenza ν=E/h in un mezzo con indice di rifrazione proporzionale a

per le onde di de Broglie l’indice di rifrazione è dunque rappresentato da una funzione del potenziale e inoltre dipende da ν, come avviene per la luce nei mezzi dispersivi. Se la particella non è soggetta a forze, è U=0, e per la velocità di fase si ha allora

,

da questa espressione e dalla relazione λν=V, valida per ogni propagazione ondosa, si ottiene

ricordando poi l’espressione della velocità di gruppo, che ora si riduce a

,

si giunge alla lunghezza d’onda di de Broglie

[12] formula,

ove p indica la quantità di moto della particella. A ogni particella risulta così ‘associata’ una lunghezza d’onda inversamente proporzionale alla quantità di moto. La ψ della forma [10] ha una frequenza unica, e quindi rappresenta onde analoghe alla luce monocromatica: si può anche avere però una ψ che sia la somma di più termini della forma [10] con diverse ν, e questa rappresenterà, se la ψ totale soddisfa la [9], una particella la cui energia non è fisicamente determinata. La ψ, in questo caso più generale, soddisfa, anziché la [11], l’equazione seguente:

[11′] formula.

Autovalori e autofunzioni Il problema di determinare una funzione ψ che soddisfi alla [11] e alla [9], e che inoltre sia finita e continua in tutto lo spazio suscettibile di essere occupato dalla particella, è matematicamente identico al problema acustico di determinare le onde stazionarie che si possono stabilire in detto spazio con una data distribuzione della densità del mezzo. Si dimostra che esso ammette soluzione soltanto se il parametro E che figura nella [11] assume particolari valori che si dicono autovalori dell’equazione e definiscono, mediante la relazione E=hν, le frequenze delle onde stazionarie. Tali autovalori sono sempre in numero infinito e possono costituire una successione discreta o anche, almeno in parte, riempire un intervallo continuo che si dice spettro continuo di autovalori. Nel primo caso l’equazione di Schrödinger conduce a stabilire l’esistenza negli atomi di livelli energetici discreti (che è un fatto sperimentalmente accertato) non attraverso un postulato come faceva la teoria di Bohr, ma mediante lo stesso procedimento matematico con il quale in acustica si stabilisce che una corda può vibrare solo con determinate frequenze. A ogni autovalore E_n può corrispondere una sola soluzione ψ_n (normalizzata) che si dice autofunzione, e allora l’autovalore si dice semplice; oppure vi possono corrispondere infinite autofunzioni che si possono tutte ottenere come combinazioni lineari di un certo numero p di esse, indipendenti fra loro: allora l’autovalore si dice multiplo d’ordine p (caso della degenerazione). Due autofunzioni corrispondenti ad autovalori diversi godono della cosiddetta proprietà di ortogonalità:

,

dove l’integrale è esteso a tutto lo spazio e l’asterisco denota il complesso coniugato.

Sviluppo e applicazioni La teoria e i risultati ai quali essa ha condotto, in particolare nella fisica atomica, hanno consentito tra l’altro di eliminare ipotesi arbitrarie e incertezze di interpretazione di risultati precedenti. Alcune modifiche successivamente (1928) apportate da P.A.M. Dirac nella impostazione stessa della m. ondulatoria, per metterla in accordo con il principio di relatività ristretta, hanno consentito di ricavare quelle proprietà dell’elettrone che nella precedente teoria dei quanti erano state introdotte a priori da G.E. Uhlenbeck e S.A. Goudsmit con l’ipotesi detta dell’elettrone rotante, e cioè l’esistenza di un momento di quantità di moto (lo spin) uguale a ±h/4π e di un momento magnetico uguale a un magnetone di Bohr e di orientamento opposto. Un ulteriore sviluppo della teoria, dovuto allo stesso Dirac, rende conto delle proprietà dell’elettrone positivo, o positrone, e in particolare della possibilità di ‘combinazione’ di un elettrone positivo e di un elettrone negativo, con annullamento delle cariche elettriche e delle masse ed emissione di radiazione (annichilazione).

Tra le più notevoli applicazioni della m. quantistica ricorderemo la teoria dell’emissione di particelle α da parte dei nuclei radioattivi, dovuta a G. Gamow (1928), che costituisce il primo esempio di applicazione alla fisica nucleare; la teoria dell’urto fra elettroni e atomi e tra atomi (o ioni) dovuta a M. Born, N.F. Mott e altri; la teoria della conduzione elettronica e quella del dia- e del paramagnetismo (➔ magnetismo); la teoria della radiazione, dovuta principalmente a Dirac, che, trattando come un solo sistema l’atomo e il campo elettromagnetico della radiazione, rende ragione degli scambi di energia tra essi e permette di calcolare intensità, frequenza e stato di polarizzazione delle radiazioni assorbite ed emesse nei processi atomici.

Sulle variabili nascoste in m. quantistica ➔ nascoste, variabili.

Meccanica dei sistemi continui

Parte della m. in cui i corpi vengono schematizzati in ‘continui’, cioè in sistemi nei quali la materia si pensa distribuita con continuità, a seconda dei casi in un volume, su una superficie o lungo una linea (continui tri-, bi- o unidimensionali); la legge di distribuzione è individuata al generico istante dalla funzione che esprime come vari da punto a punto la densità. Per la tale definizione, la m. dei sistemi continui dovrebbe a rigore comprendere sia la m. dei continui deformabili sia quella dei continui rigidi; in realtà abitualmente questa si tiene distinta dalla prima, poiché sono diversi i criteri d’impostazione e di sviluppo, così la locuzione è usata come sinonimo di meccanica dei sistemi deformabili. Nello sviluppo della teoria in un primo tempo non sono in alcun modo precisate le proprietà fisiche caratteristiche del corpo in esame, ed essa riguarda indifferentemente liquidi, aeriformi, corpi elastici ecc. In una fase successiva, precisando tali proprietà, la teoria si specializza in fluidomeccanica, elastomeccanica ecc. La m. dei sistemi continui può essere sviluppata da due punti di vista: cioè il punto di vista molecolare, o lagrangiano, che considera le varie grandezze in corrispondenza alle singole particelle del sistema, e il punto di vista locale, o euleriano, che le riferisce invece al generico punto dello spazio occupato dal sistema medesimo. Il sistema è in generale sottoposto a un certo insieme di forze, superficiali e di massa: ne nascono tensioni interne, incognite, che intervengono nel determinare l’andamento, pure generalmente incognito, della densità e del moto, o con riferimento alle singole particelle (impostazione lagrangiana) o con riferimento ai singoli punti dello spazio (impostazione euleriana).

Per determinare lo stato interno di tensione, si deve determinare la distribuzione degli sforzi specifici che al generico istante si crea intorno a ogni punto. Lo sforzo specifico, Φ⁽ⁿ⁾ (P, t), che si esercita all’istante t sull’elemento di superficie condotto per un punto P e individuato, quanto alla giacitura, dalla sua normale orientata, n, fermi restando P e t, varia al variare di n a norma del cosiddetto teorema del tetraedro di Cauchy. Precisamente, se si sceglie una terna di assi ortogonali x₁, x₂, x₃, con origine in P, e considerati tre elementi di superficie aventi come normali orientate, rispettivamente, i semiassi positivi x₁, x₂, x₃, si indicano con Φ⁽¹⁾, Φ⁽²⁾, Φ⁽³⁾ gli sforzi specifici relativi ai tre elementi suddetti, lo sforzo specifico relativo all’elemento di superficie avente per normale n può essere espresso nella forma

Φ⁽ⁿ⁾ = Φ⁽¹⁾ n₁ + Φ⁽²⁾ n₂ + Φ⁽³⁾ n₃,

essendo n₁, n₂, n₃ i coseni direttori di n. In altre parole, la conoscenza della distribuzione degli sforzi specifici intorno a ciascun punto richiede la conoscenza delle componenti dei tre vettori Φ⁽¹⁾, Φ⁽²⁾, Φ⁽³⁾, componenti che verranno qui indicate con il simbolo Φ_rs, essendo r, variabile da 1 a 3, l’indice dell’asse cui si riferisce la componente, e s, pure variabile da 1 a 3, l’indice dell’asse cui si riferisce lo sforzo (così, per es., Φ₂₃ indicherà la componente secondo l’asse x₂ di Φ⁽³⁾). Le Φ_rs, che in definitiva individuano il tensore degli sforzi, sono 9 quantità scalari, ma, come si dimostra, 6 soltanto di esse (caratteristiche di tensione) sono fra loro distinte, valendo le cosiddette relazioni di simmetria per le quali Φ_rs=Φ_sr (r≠s). La distribuzione degli sforzi specifici introduce pertanto in corrispondenza a ogni punto 6 incognite. A esse vanno aggiunte la densità e altre 3 incognite scalari per la determinazione del moto (per es., dal punto di vista euleriano le 3 componenti della velocità espresse in funzione del posto e del tempo). Si hanno così, complessivamente, nel caso più generale, punto per punto, 10 incognite, laddove punto per punto si hanno a disposizione soltanto 4 equazioni. Queste sono la cosiddetta equazione di continuità, in cui analiticamente si traduce il principio della conservazione della massa, e le 3 equazioni scalari corrispondenti alla equazione fondamentale della m. dei sistemi continui. In forma euleriana l’equazione di continuità, ove si indichino con x₁, x₂, x₃ le coordinate del posto, con ρ (x₁,x₂,x₃,t) e con v(x₁,x₂,x₃,t) rispettivamente le espressioni locali della densità e della velocità, con t il tempo, si può scrivere

,

essendo ∂ρ/∂t la derivata parziale (o euleriana) della densità rispetto al tempo: si tratta in sostanza di una equazione alle derivate parziali del prim’ordine nelle variabili indipendenti t, x₁, x₂, x₃ per le 3 componenti v₁, v₂, v₃ del vettore v e per la funzione ρ. Sempre in forma euleriana, le 3 equazioni scalari fondamentali, mantenendo agli altri simboli il significato precedentemente detto e indicando con a(a₁,a₂,a₃) l’accelerazione, con g(g₁,g₂,g₃) la forza unitaria di massa, si possono scrivere nella forma

,

con s=1, 2, 3. Le 4 equazioni suddette si dicono indefinite in quanto devono essere verificate nel generico punto del sistema. Il quadro delle relazioni fondamentali si completa con l’aggiunta delle condizioni al contorno, riassumibili nell’eguaglianza, vettoriale, fra l’intensità f della forza superficiale esterna e lo sforzo specifico Φ⁽ⁿ⁾, valutato rispetto alla normale interna n alla superficie di contorno:

f = Φ⁽ⁿ⁾.

Ben naturale appare la larga indeterminazione che si viene ad avere (4 equazioni contro 10 incognite) se si riflette all’ampia generalità dell’impostazione, cioè alla mancanza di qualsiasi precisazione circa particolari proprietà da attribuire al sistema: un corpo elastico e un liquido, per es., possono ambedue essere rappresentati mediante un sistema continuo deformabile, ma è ben evidente che il comportamento dell’uno non è quello dell’altro e che quindi le equazioni valide per il primo non potranno essere in tutto le stesse che per il secondo. Caso per caso l’indeterminazione si elimina dunque tenendo conto di particolari proprietà, ciò che può dar luogo a una riduzione di incognite o all’aggiunta di equazioni. Se, per es., si ha a che fare con un fluido non viscoso, lo sforzo specifico è, come si dimostra, in ogni punto una pressione, con uno stesso valore qualunque sia la direzione che si considera: in tal caso le caratteristiche di tensione da 6 si riducono a una, cioè alla incognita pressione, e si ha soltanto un’incognita in più rispetto al numero delle equazioni. Se, inoltre, si aggiunge l’ipotesi che il fluido non viscoso sia un liquido incompressibile, la densità, non potendo variare nell’intorno di ciascun punto, esce dal numero delle incognite e si raggiunge la parità fra equazioni e incognite senza che sia necessario aggiungere alle 4 equazioni di base altre relazioni.

Meccanica statistica

Parte della m. che si propone di dedurre le proprietà dei sistemi macroscopici dall’ipotesi atomica, secondo la quale la materia è costituita da aggregati di un grandissimo numero di atomi o molecole che si muovono seguendo le leggi della m. classica o della m. quantistica; la corrispondente teoria prende il nome di meccanica statistica classica o meccanica statistica quantistica. Le complicazioni matematiche alle quali si andrebbe incontro, se si volesse studiare con i metodi della m. ordinaria (classica o quantistica) il moto di un sistema costituito da un numero enorme di particelle, sarebbero molto grandi. D’altra parte per caratterizzare un sistema macroscopico è sufficiente un numero relativamente piccolo di parametri, cioè quelli necessari per specificare il suo stato termodinamico (come, per es., temperatura, pressione, magnetizzazione ecc.); quindi una eventuale soluzione delle equazioni del moto, dipendendo dall’enorme numero di parametri relativi alle particelle che costituiscono il sistema, sarebbe inutilmente dettagliata. Compito della m. statistica è fornire le prescrizioni e le giustificazioni per effettuare l’eliminazione dei parametri microscopici irrilevanti, e passare a una descrizione macroscopica, cioè termodinamica.

Meccanica statistica classica Nella m. classica gli stati microscopici di un sistema costituito da N particelle sono descritti specificando il valore delle quantità di moto e delle posizioni di ciascuna delle particelle a un dato istante; nell’ipotesi che la determinazione di tali valori possa avvenire con precisione illimitata, ciò equivale a specificare le 3N+3N coordinate che individuano un punto nello spazio delle fasi del sistema in esame. Tuttavia questa assunzione accetta per evidente un fatto che tale non è da un punto di vista sperimentale, cioè che abbia senso, almeno in linea di principio, misurare con esattezza e contemporaneamente posizioni e velocità di un enorme numero di molecole. Conviene allora procedere pensando lo spazio delle fasi suddiviso in piccolissime cellette di uguali dimensioni, ognuna delle quali determina quantità di moto e posizione di ogni particella del sistema, con la massima precisione consentita. Se p₁, p₂, p₃ e q₁, q₂, q₃ sono le coordinate di quantità di moto e posizione della prima particella, p₄, p₅, p₆ e q₄, q₅, q₆ quelle della seconda ecc., gli stati microscopici del sistema possono essere rappresentati da cellette costituite dai punti di coordinate:

con la condizione δpδq=h, dove con h è da intendersi una costante, a priori arbitraria, che ha l’interpretazione di limitazione alla precisione con cui sono eseguibili misure di una coordinata di quantità di moto e della corrispondente coordinata di posizione. Le coordinate p⁰_αe q⁰_α servono a identificare il centro della generica celletta e quindi la celletta stessa. Lo spazio degli stati microscopici è perciò l’insieme delle cellette Δ, di volume h^3N, con le quali si pensa suddiviso lo spazio delle fasi. La situazione in cui è possibile eseguire misure perfette di quantità di moto e posizione simultaneamente, corrisponde al limite h che tende a zero nella teoria più generale. Per tradurre il principio del meccanicismo insito nell’ipotesi atomica, è necessario definire una legge S, che descrive la dinamica del sistema trasformando le cellette dello spazio delle fasi tra loro: se il sistema al tempo t è individuato dalla celletta Δ, al tempo t+τ sarà individuato dalla celletta Δ′=SΔ; τ è una unità di tempo piccola rispetto agli intervalli di tempo macroscopici sui quali si osserva il sistema, tuttavia accessibile a misurazione diretta, almeno in linea di principio. La legge di evoluzione S deve verificare le leggi della m. newtoniana; ciò significa che a ogni celletta sono associate 3 grandezze fondamentali: l’energia cinetica T(Δ)=T(p⁰), quella potenziale Φ(Δ)=Φ(q⁰), quella totale H(Δ)=H(p⁰, q⁰)=T(p⁰)+Φ(q⁰), dove p⁰_i e q⁰_i sono la quantità di moto e la posizione della i-ma particella (i=1,...,N) nello stato corrispondente al centro (p⁰, q⁰) di Δ. Date le soluzioni delle equazioni del moto di Hamilton:

se Δ′ è la celletta che contiene il punto in cui evolve il dato iniziale (p⁰, q⁰) nel tempo τ, si definisce S in modo che sia SΔ=SΔ′. Molto importante è la questione se SΔ₁=SΔ₂ implichi Δ₁=Δ₂: questa proprietà, che ha un significato intuitivo e un interesse evidenti per la sua connessione con il problema della reversibilità del moto, è certamente vera solo nel caso delle cellette puntiformi (h=0). Nel limite h→0 è possibile scegliere τ in modo che, a meno di un insieme trascurabile di coppie di cellette, Δ₁≠Δ₂ implichi SΔ₁≠SΔ₂. Se invece h>0, e a posteriori si deve pensare che h sia la costante di Planck, tale condizione è soddisfatta solo per temperature sufficientemente elevate; in caso contrario, la rappresentazione degli stati microscopici in termini di cellette non è più consistente, ma in tal caso il problema dovrebbe essere trattato con la m. quantistica. Un sistema meccanico di N particelle identiche si può quindi descrivere, per temperature non troppo basse, in termini di una funzione energia, definita sullo spazio delle fasi a 6N dimensioni suddiviso in cellette di uguale volume; l’evoluzione temporale, osservata su intervalli di tempo multipli di una unità τ, va pensata come una permutazione di cellette di data energia. Ci si domanda quale sia il comportamento qualitativo di tale sistema con energia fissata macroscopicamente, cioè compresa tra E−DE e E, essendo DE una quantità piccola rispetto a E ma macroscopica. L. Boltzmann suppose che nei casi interessanti valesse l’ipotesi ergodica, secondo la quale l’azione di S è la più semplice possibile: S è una permutazione a un solo ciclo delle cellette della data energia. In altre parole: al passare del tempo ogni celletta evolve visitando successivamente tutte le altre di uguale energia. Il fondamento di questa celebre e contestata ipotesi è la sua semplicità concettuale: essa dice che, nel sistema in questione, tutte le cellette di uguale energia sono equivalenti. Ci sono dei casi in cui questa ipotesi è manifestamente falsa; per es., se il sistema è racchiuso in un contenitore sferico perfetto, l’evoluzione conserva il momento angolare per cui cellette con uguale energia ma diverso momento angolare non possono trasformarsi una nell’altra.

Data una grandezza osservabile definita sullo spazio delle fasi, f(p, q), una quantità importante che si vuole studiare, e spesso l’unica necessaria, è la media temporale di f:

[13] formula,

dove f(Δ) = f(p, q) se (p, q) è un punto che individua Δ. Se Δ₁ = Δ, Δ₂, Δ₃, ..., ΔN è il ciclo cui appartiene la celletta Δ si ha:

[14] formula,

e nel caso ergodico il ciclo consiste nell’insieme di tutte le cellette di energia uguale a quella di Δ. Se l’energia del sistema è determinata a meno dell’errore DE, le cellette di energia tra E−DE e E sono suddivise in cicli di energia variabile, su ciascuno dei quali la f dovrebbe avere lo stesso valor medio (a meno di variazioni trascurabili, se DE è trascurabile rispetto a E). Quindi, ricordando che le cellette hanno tutte lo stesso volume e indicando con J il dominio delle variabili (p, q) in cui E−DE ≤H(p,q)≤E, per la supposta debole dipendenza dif̅(Δ) da H(Δ) dalla [14] segue:

[15] formula,

se h è così piccola che la somma sulle cellette può essere sostituita con un integrale. Questa relazione, che Boltzmann congetturò essere vera salvo casi eccezionali, si legge: «la media temporale di un’osservabile è uguale alla sua media sulla superficie di energia costante». Essa è la base euristica del modello microcanonico della termodinamica classica. Si noti che, se è vera la [15], il valor medio di un’osservabile dipende solo da E e non dalla particolare celletta in cui il sistema si trova inizialmente. Quest’ultima proprietà è un prerequisito necessario a ogni programma che intenda dedurre le proprietà macroscopiche della materia dall’ipotesi atomica, in quanto tali proprietà non possono dipendere dalle dettagliate proprietà microscopiche della configurazione in cui il sistema viene a trovarsi a un determinato istante. Nelle applicazioni ha grande importanza saper valu;tare la velocità con cui il limite f̅ viene raggiunto: perché la [15] sia utile occorre che il limite nella [13] sia raggiunto in un tempo t lungo rispetto a τ, ma molto corto rispetto ai tempi rilevanti per le osservazioni macroscopiche che si vogliono eseguire sul sistema. Infatti solo su scale di tempo dell’ordine di t o più lunghe l’osservabile f appare costante e uguale al suo valor medio. È perfettamente concepibile una situazione in cui il sistema è ergodico, ma il valore f(Δ) oscilla talmente lungo la traiettoria che il valor medio di f è raggiunto su scale di tempo dell’ordine di grandezza del tempo necessario a visitare tutta la superficie di energia costante (tempo di ricorrenza), che è enorme. Per es., per 1 cm³ di idrogeno a 0 °C tale tempo è dell’ordine di 10¹⁰¹⁹ s, mentre l’età dell’Universo è (solo) ≈ 10¹⁷ s!

Meccanica statistica quantistica La m. statistica quantistica è assai simile a quella classica dal punto di vista della struttura formale. Lo spazio delle fasi non ha più senso e invece si pensa solo all’insieme delle grandezze osservabili: esse sono descritte da operatori lineari su uno spazio di Hilbert e gli insiemi statistici sono definiti in termini dell’operatore che descrive l’energia, di solito denotato con H e detto operatore di Schrödinger.