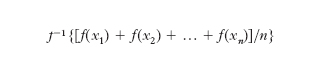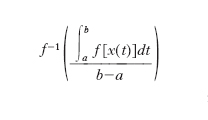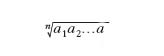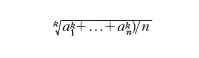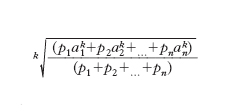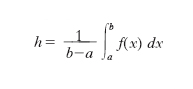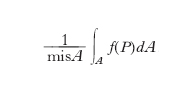media

Valore generalmente intermedio, determinato secondo vari criteri matematici o statistici, tra i valori assunti da una grandezza della stessa specie.

Media dei dati

In varie questioni matematiche e, in particolare, di statistica si rende spesso necessario valutare quantitativamente un insieme di dati numerici mediante uno o più parametri caratteristici dell’insieme; tra questi, la m. dei dati è un parametro di localizzazione, nel senso che può essere opportunamente interpretata come quel valore numerico costante intorno a cui si distribuiscono i dati o è maggiore la probabilità che vi si concentrino. Supposto, per semplicità, che i valori dei quali si vuole considerare una m. siano x₁, x₂, ..., x_n, e dunque in numero finito, si tratta di ottenere a partire da essi un numero spesso indicato con M, m, μ o più propriamente in statistica con E (dall’ingl. expectation) che: a) sia compreso tra il minimo e il massimo degli x₁, ..., x_n e in particolare, perciò, sia uguale a ciascuno di essi nel caso in cui essi siano uguali; b) non dipenda dall’ordine nel quale si considerano i numeri x₁, ..., x_n.

Un procedimento di carattere generale per ottenere una m. di n valori consiste nello scegliere una qualsiasi funzione f(x) che possieda una funzione inversa f⁻¹(x); di solito si sceglie una f(x) sempre crescente o viceversa sempre decrescente nell’intervallo che occorre considerare; una m. dei valori x₁, ..., x_n è allora data da

[1] formula.

Scegliendo, in particolare, f(x)=x oppure f(x)=logx, o f(x)=1/x o infine f(x)=x², la [1] dà quattro dei più comuni tipi di m.: rispettivamente le m. aritmetica, geometrica, armonica, quadratica.

fig. 1

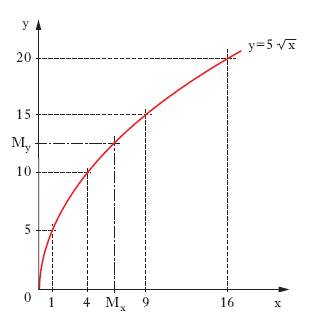
La [1] consente anche una semplice costruzione geometrica di M (fig. 1); tracciato il grafico della funzione y = f(x) la m. M_x dei valori x₁, ..., x_n è l’unico valore di x al quale corrisponde per la y il valore

M_y = [f(x₁)+...+f(x_n)]/n:

in un certo senso, perciò, ogni m. ottenuta tramite la [1] è riconducibile a una m. aritmetica.

Nel caso in cui i valori dei quali si deve calcolare la m. siano in numero infinito, per es. i valori assunti da una funzione x=x(t) al variare di t in un certo intervallo a ≤ t ≤ b, la somma indicata nella [1] si modifica in un integrale e la formula diviene:

[2] formula.

Il concetto di m. si estende poi, in vari modi, a casi ancora più generali (m. di valori complessi, m. in un intervallo illimitato ecc.).

Statistica

Per quanto riguarda la statistica, e quindi anche tutte le scienze sperimentali che si avvalgano di metodi statistici, è opportuno considerare una m. quando l’osservazione di un fenomeno dà luogo alla rilevazione di una pluralità di dati numerici non tutti uguali e si presenta la necessità di valutare quantitativamente l’andamento o il carattere del fenomeno mediante un solo parametro numerico costante. La m., quale sintesi delle osservazioni, viene quindi a sostituirsi alla molteplicità dei dati rilevati; ne consegue una perdita di informazioni che potrà essere espressa, o per lo meno approssimata, da una funzione che dipenderà dalla m. e dai valori osservati; la forma di tale funzione sarà determinata dalla natura dello studio che si intende svolge;re o del fenomeno esaminato, e varierà quindi a seconda delle circostanze. Scelta comunque una funzione, G (a₁, a₂, ..., a_n, m), che misura tale perdita di informazione, dove a₁, a₂, ..., a_n sono i valori osservati, la m. m risulta definita dalla condizione di rendere minima la funzione G. Così, per es., se

G = |(a₁−m) + (a₂−m) + ... + (a_n−m)|

oppure

G = (a₁−m)² + (a₂−m)² + ... + (a_n−m)²,

il minimo si realizza quando m è la m. aritmetica; se G=|a₁−m|+|a₂−m|+...+|a_n−m|, m deve essere la mediana (➔); e così via. Con tale impostazione, il concetto di m. può essere esteso abbastanza agevolmente a distribuzioni di caratteri qualitativi.

Principali tipi di media

M. di un numero finito di valori. - A seconda della natura dello studio che si intende svolgere o del fenomeno esaminato, si usano, per un dato insieme di valori, o seriazioni, vari tipi di m.: m. in senso stretto o effettiva o reale, è uno qualsiasi dei valori della seriazione che non sia né inferiore, né superiore a tutti gli altri; m. in senso lato è un qualunque valore compreso tra i valori di due elementi della seriazione; m. di conto è una m. in senso lato che non coincida con alcun termine della seriazione; m. analitica è quella che si calcola mediante un’espressione analitica, piuttosto semplice a partire dai termini della serie; m. di posizione è una m. che si definisce mediante la sua posizione nell’ordinamento dei termini della seriazione; m. lasca è una m. che tiene conto solo di taluni termini della seriazione, basandosi sulla loro frequenza, posizione ecc. (le m. lasche più usate sono la moda e la mediana); m. ferma è una m. che tiene conto di tutti i termini; m. semplice è una m. che considera tutti i termini alla stessa stregua; m. ponderata (o pesata) è una m. che distingue la diversa importanza (peso) da darsi ai vari termini.

M. ferme semplici. - Essendo a₁, a₂, ..., a_n i termini della seriazione, le m. ferme semplici più usate sono la m. aritmetica: (a₁+a₂+...+a_n)/n; la m. geometrica:

la m. armonica: n/[(1/a₁)+(1/a₂)+...+(1/a_n)]; la m. antiarmonica: (a₁²+a₂²+...+a_n²)/(a₁+a₂+... +a_n); le m. di potenze di ordine k:

M. ferme ponderate. - Essendo p₁, p₂, ..., p_n i pesi degli elementi sopra considerati, le più usate sono la m. aritmetica ponderata: (p₁a₁+p₂a₂+...+p_na_n)/(p₁+p₂+...+p_n); la m. geometrica ponderata: (a^p₁¹a^p₂²…a^p_nⁿ)^{1/(p1+p2+...+pn)}; la m. armonica ponderata: (p₁+p₂+...+p_n)/[(p₁/a₁)+(p₂/a₂) +...+(p_n/a_n)]; la m. antiarmonica ponderata: (p₁a₁²+p₂a₂²+...+p_na_n²) / (p₁a₁+p₂a₂+...+p_na_n); la m. di potenze di

ordine k ponderata:

M. mobile.- Un tipo particolare di m., cui si ricorre per eliminare o attenuare l’influenza di certi fattori, e in particolare di fattori accidentali nelle seriazioni temporali, è la m. mobile. Se a₁, a₂, ..., a_n sono i valori osservati agli istanti t₁, t₂, ..., t_n, fissato un intero positivo h<n/2, la m. mobile di modulo h dell’elemento a_t (con h<t<n−h+1) è la m. aritmetica semplice dei (2h+1) termini

a_t–h, a_t–h+1, ..., a_t, ..., a_t+h–1, a_t+h.

fig. 2

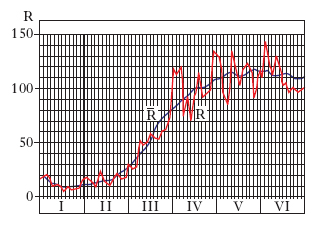
In fig. 2 sono riportati, a titolo di esempio, gli andamenti del numero medio mensile delle macchie solari (R, in rosso) e della m. mobile a 13 mesi (R̅, in nero), ottenuta sostituendo al valore di ogni mese la m. aritmetica semplice dei valori dei 13 mesi centrati sul mese in questione: come si vede, attenuando fortemente la variazione annua, la m. mobile evidenzia nella grandezza un andamento a lungo termine molto più regolare.

M. di una funzione. - Il caso più semplice è quello di una funzione reale f(x), definita nell’intervallo (a, b) dell’asse reale, e ivi integrabile: m. (o valor medio) della f(x) è il valore

fig. 3

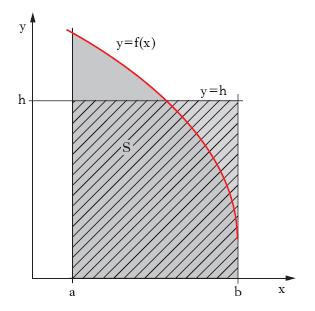
Il significato geometrico di tale numero è semplice: se si considera l’area S della regione piana limitata dalla curva y=f(x), dalle rette x=a, x=b e dall’asse delle x (in grigio in fig. 3), e si desidera sostituire alla y=f(x) una retta parallela all’asse x in modo però che il rettangolo ottenuto (segnato con linee oblique) abbia ancora area S, la retta deve essere la y=h. Nel caso di una funzione di più variabili, f (P) definita in un dominio misurabile A e ivi integrabile, si intende per m. il valore