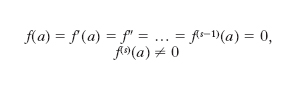molteplicità
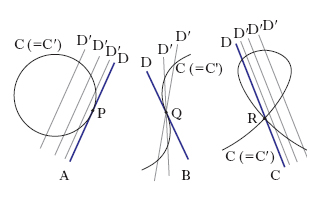
molteplicità In matematica, m. d’intersezione di più varietà algebriche in un punto comune è il numero intero positivo che si associa a ogni punto comune a due o più varietà algebriche e che denota (in un certo senso) quanti punti comuni alle varietà in questione siano da intendersi coincidenti nel punto considerato, o, in altre parole, quante volte quest’ultimo si debba ripetere quando si contano i punti di intersezione delle varietà. La definizione rigorosa di m. d’intersezione si dà in vari modi, algebrici o analitici, e distinguendo più casi a seconda del numero e delle dimensioni delle varietà che si intersecano. Per es., per valutare la m. d’intersezione di due curve algebriche piane C, D, di ordini m, n, in un loro punto P, si considerino due curve generiche C′, D′, dello stesso ordine di C e D: C′, D′ si intersecano in m ∙ n punti semplici. Se C′, D′ tendendo a C, D in tutti i modi possibili, rimangono generiche, e accade che un numero costante v degli m ∙ n punti suddetti tende al punto P, v è la m. d’intersezione di C e D in P. Per es., la m. d’intersezione tra una curva C (fig. A) e la sua tangente D, in un punto ordinario P è 2; in un flesso ordinario Q è 3 (fig. B); in un punto doppio R di una curva, la m. d’intersezione tra la curva e una retta generica per il punto è 2 (fig. C).
M. di un punto per una varietà algebrica Data una varietà algebrica pura V di dimensione k, immersa in uno spazio a r dimensioni, un suo punto si dice s-plo, o di m. s, se è s la m. d’intersezione in P di V con uno spazio generico per P, avente dimensione r −k. In particolare, un punto P di una curva piana si dice di m. s se una retta generica per P ha con la linea in P, m. d’intersezione s.
M. di una radice di un’equazione algebrica Data un’equazione algebrica f(x)=0 di ordine n, e una sua radice α reale o complessa, si dice che α è radice s-pla, o di m. s (naturalmente è 1 ≤s ≤n), se accade che f(x) è divisibile per (x − α)s e non per (x − α)s+1. Con lo stesso significato si parla anche di m. degli zeri della funzione f(x). Per riconoscere la m. di una radice vale il seguente teorema: se e solo se α è radice s-pla dell’equazione f(x) = 0, si ha
dove f(h)(α) indica la derivata h-esima f(h)(x) del polinomio f(x), calcolata per x = α.