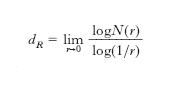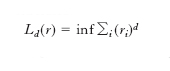dimensione

Fisica

Numero che indica in qual modo le grandezze fondamentali intervengono nelle singole grandezze derivate, individuandone l’unità di misura in funzione delle unità fondamentali. Una certa grandezza A è una grandezza fisica in quanto suscettibile di misurazione: prescelta una grandezza U della stessa specie di A come unità di misura è possibile determinare il rapporto tra A e U, che ha il nome di ‘misura di A rispetto a U′; pertanto una grandezza fisica è il prodotto di un numero (la misura) per un’unità di misura. Nulla vieta, a priori, di assumere per le varie specie di grandezze unità di misura scelte indipendentemente una dall’altra; così facendo, nelle relazioni tra misure di grandezze diverse vengono a comparire necessariamente fattori numerici, i cosiddetti ‘coefficienti parassiti’. Se si esige che, com’è conveniente, tali coefficienti scompaiano o siano ridotti a pochi casi, se cioè si esige un sistema di unità di misura coerente, occorre scegliere alcune grandezze e le relative unità di misura come fondamentali e derivare da esse, per il tramite di relazioni di definizione, le unità di misura delle altre grandezze. Scelte le grandezze fondamentali, ciascuna delle altre, dette perciò ‘derivate’, si presenta sempre come prodotto o rapporto di grandezze fondamentali, alla misura delle quali viene quindi a essere riportata la misura della grandezza derivata. Così, un’area è data in ogni caso dal prodotto di due lunghezze; una velocità è il rapporto di una lunghezza a un tempo ecc. Tutto ciò si esprime dicendo che le d. di ciascuna grandezza derivata sono sempre quelle del prodotto delle grandezze fondamentali elevate ciascuna a un opportuno esponente; più esattamente il termine d. sta a indicare questi esponenti, ciascuno dei quali può essere, a seconda dei casi, positivo, negativo o nullo. Si può dire indifferentemente che le d. della velocità sono quelle del prodotto di una lunghezza per l’inverso di un tempo, ovvero che essa ha d. 1 rispetto alla lunghezza e −1 rispetto al tempo; una superficie ha d. 2 rispetto alla lunghezza, zero rispetto al tempo. Se tutte le d. sono nulle, la grandezza in questione è, nel prescelto sistema di unità di misura, adimensionata; sono adimensionate, in generale, tutte le grandezze fisiche definite come rapporto tra grandezze della stessa specie (per es. gli angoli).

Matematica

Si dice che il piano ordinario è un ente a 2 d. perché la posizione di un suo punto P è individuata da una coppia ordinata di numeri reali (per es., le distanze con segno di P da due rette tra di loro ortogonali); analogamente, si dice che lo spazio ordinario è un ente a 3 d.; in generale si chiama spazio euclideo a n d. l’insieme delle n-ple ordinate (x₁,x₂,...,x_n) di numeri reali. Da questo punto di vista, le d. di un ente geometrico appaiono come i parametri necessari per individuare un punto di esso. Si noti che l’affermazione ‘il piano ha 2 d.’ significa non solo che i punti del piano (o di una sua parte, per es. di forma quadrata) si possono individuare biunivocamente mediante 2 numeri reali, ma che questa corrispondenza è ‘bicontinua’, cioè a piccoli spostamenti del punto corrispondono sempre piccole variazioni per le coordinate, e viceversa. È, infatti, possibile rappresentare biunivocamente i punti di un quadrato mediante una sola coordinata, ma inevitabilmente accade che vi sono piccoli spostamenti del punto a cui corrisponde una non piccola variazione dell’unica coordinata. Ciò indica che la d. sopra introdotta è una proprietà di carattere topologico; essa viene anche detta d. topologica per distinguerla da altri tipi di d., introdotte nello studio di strutture geometriche ‘non regolari’ (➔ frattale), caratterizzate dal fatto di poter assumere valori non interi e, per questo, dette anche genericamente d. frattali. Tra esse hanno rilievo la d. di ricoprimento (o capacitaria) e la d. di Hausdorff-Besikovich. La d. di ricoprimento di un sottoinsieme limitato E di uno spazio metrico, cioè sul quale è data una nozione di distanza, è definita da

,

dove N(r) è il numero minimo di sfere di raggio r necessarie per ricoprire E. La d. di Hausdorff-Besikovich di E, d_H, è definibile considerando la funzione

,

dove d > 0 e l’estremo inferiore è inteso rispetto ai ricoprimenti finiti di E con sfere di raggi ri 〈 r; al decrescere di r, L_d (r) cresce e converge a un limite: F. Hausdorff ha dimostrato che esiste un numero reale d_H tale che, se L_d indica il limite di L_d (r) per r → 0, si ha L_d = 0 per d 〈 d_H e L_d=∞ per d > d_H.