area

Biologia

In embriologia, il termine designa varie formazioni che si osservano durante lo sviluppo embrionale dei Vertebrati in genere e degli Amnioti in particolare. Nelle uova degli Uccelli, per es., a. germinativa (o disco germinativo) è il dischetto localizzato a un polo dell’uovo che, segmentandosi durante la discesa dell’uovo stesso nell’ovidutto, dà origine al blastoderma. Durante le prime ore d’incubazione l’a. germinativa diviene ovale e allungata e in essa si vengono a distinguere una parte centrale ( a. pellucida) più trasparente perché più sottile e perché si è sollevata dal sottostante tuorlo, e una parte periferica detta a. opaca per la sua minore trasparenza dovuta al maggiore spessore. La porzione centrale dell’a. pellucida da cui si originano la linea primitiva, il nodo primitivo, il prolungamento cefalico, formazioni tutte che preludono alla costituzione del futuro embrione, prende il nome di a. embrionale. La restante porzione di a. pellucida e l’a. opaca costituiscono l’ a. extraembrionale che non partecipa alla formazione del corpo dell’embrione, ma a quella dei vari annessi embrionali. Quando il disco embrionale nella sua crescita si è esteso notevolmente, nella regione dell’a. opaca si distingue una zona interna, nella quale sono presenti i tre foglietti embrionali e dove si formeranno i vasi sanguigni ( a. vasculosa), da una zona esterna ( a. vitellina), che corrisponde al margine di rivestimento.

Nei Mammiferi, a. centrale è l’accumulo di elementi (bottone o gemma embrionale) che, alla fine della segmentazione, si trova attaccato alla parete della blastocisti e che viene a corrispondere all’a. embrionale.

Geografia

A. marina protetta

A. marina protetta In ecologia, ambienti marini (acque, fondali e tratti di costa prospicienti) di rilevante interesse per le caratteristiche naturali, con particolare riguardo alla flora e alla fauna marine e costiere, e di intrinseca importanza scientifica, ecologica, culturale, educativa ed economica, posti sotto tutela per molteplici ragioni di ordine sociale, scientifico ed economico: mantenimento di strutture e processi ecologici di base, conservazione della diversità (genetica, tassonomica ecc.) degli organismi che vivono in queste a. e garanzia di una fruizione sostenibile delle specie e degli ecosistemi. In Italia, a questo scopo fin dall’inizio degli anni 1980 è stata istituita la possibilità di vincolare a. di particolare interesse naturalistico. Nelle riserve naturali marine, le attività sono regolamentate con divieti e limitazioni alla navigazione, alla pesca professionale e sportiva, all’alterazione diretta o indiretta dell’ambiente, allo scarico di rifiuti e a qualsiasi altra attività che possa interferire con le finalità per cui la riserva è stata istituita.

Le a. marine protette sono generalmente divise in settori a diverso grado di tutela. La zona A è destinata a riserva integrale: la tutela del sito è assoluta e non è permessa nessuna attività (navigazione, pesca, immersioni ecc.); la zona B, a riserva generale, e la zona C, a riserva parziale, sono a. di transizione tra gli ecosistemi tutelati e il mare a libera fruizione.

A. vulcanica Regione della superficie terrestre nella quale si accentrano i vulcani. Sono a. attive quelle in cui i vulcani, di continuo o saltuariamente, sono in attività, e quiescenti le altre. Le a. vulcaniche attive si trovano allineate su particolari direttrici e corrispondono alle zone di massima instabilità terrestre: sono marginali ai continenti e coincidenti con le zone di sollevamento relativamente recenti (settore insulare giapponese, settore insulindico, settore aleutino, settore siculo ecc.).

Istruzione

Nei modelli d’istruzione secondaria di carattere unitario, a. comune è il complesso degl’insegnamenti considerati di formazione generale e previsti in tutti gli indirizzi di studio. A essi si aggiungono altri insegnamenti specifici che costituiscono l’ a. di indirizzo.

Matematica

In geometria, misura di una superficie (in rapporto ad altra assunta come unità). Il concetto intuitivo di a. e la misura dell’a. nascono dalle prime esigenze e dalle prime esperienze dell’agrimensura e rappresentano uno dei punti di partenza della geometria. Ma una definizione rigorosa e generale del concetto di a. incontra notevoli difficoltà.

Per definire l’a. di un poligono piano si può ricorrere al concetto di equivalenza. Chiamando equivalenti due poligoni quando siano decomponibili in poligoni uguali (cioè quando siano equiscomponibili), si dirà che due poligoni hanno la stessa a. quando, e soltanto quando, essi sono equivalenti (in questo modo, l’a. di un poligono viene definita per astrazione, come l’elemento comune, l’astratto, di una classe di poligoni equivalenti). Sulla base di questa definizione, si possono confrontare tra di loro le a. di poligoni e misurarle, fissata come unità di misura l’a. di un ben determinato poligono. L’unità di misura dell’a. nel sistema internazionale è il metro-quadrato (m²).

In taluni casi, di a. di regioni piane, per es. limitate da curve chiuse o di superfici curve, può accadere che non sia possibile decomporre due superfici ‘uguali per estensione’ in un numero finito di parti uguali (nel senso della congruenza). Tuttavia è possibile arrivare anche in questi casi a una definizione soddisfacente mediante un ‘passaggio al limite’.

fig.

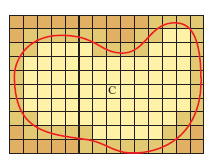
Regioni piane limitate da curve chiuse Se si vuole definire, e insieme determinare, l’a. A di una regione piana C racchiusa da una curva (non intrecciata), si può procedere nel seguente modo: si ‘quadretta’ il piano mediante due sistemi di rette parallele, tra loro ortogonali (v. fig.). Si considerano dapprima tutti i piccoli quadrati (o rettangoli) formati da tali rette e giacenti per intero dentro la regione C; si assume, in modo corrispondente all’intuizione, la somma delle a. di tali rettangolini come misura approssimata per difetto dell’a. A. La somma delle a. dei rettangolini che contengono invece anche solo qualche punto interno alla regione (ma eventualmente anche punti esterni) si assumerà come misura approssimata per eccesso di A. Infittendo via via la ‘quadrettatura’ (e cioè facendo tendere a zero la massima diagonale dei rettangolini), le misure approssimate per difetto cresceranno sempre, quelle approssimate per eccesso diminuiranno sempre. Se esse tendono a un comune ‘valore limite’, questo, l’integrale ʃʃ_cdxdy, si assumerà appunto come misura dell’a. A.

Anche il caso delle superfici sviluppabili sopra un piano si riconduce a quelli prima trattati. Negli altri casi di superfici curve, sono state proposte e discusse varie definizioni, sempre basate su ‘passaggi al limite’. Per es., l’a. su una superficie curva si può definire come il limite delle a. di una successione di superfici poliedriche iscritte, quando le facce di queste si restringono indefinitamente, e contemporaneamente i loro piani si accostino indefinitamente al piano tangente alla superficie in un vertice del poliedro. Le definizioni date (e le altre che si possono dare) soddisfano tutte le seguenti due proprietà, fondamentali nel concetto intuitivo di a.:

a) se si considerano porzioni di superficie, l’a. della superficie totale è uguale alla somma delle a. delle singole porzioni (proprietà additiva);

b) se una superficie contiene in sé interamente un’altra superficie, quest’ultima ha un’a. minore della prima.

Medicina

In neurologia:

a. corticale, porzione della corteccia cerebrale, distinta dalle circostanti per struttura istologica o per funzione;

a. di proiezione, l’a. corticale in rapporto con neuroni di moto o con organi periferici di senso;

a. di associazione, a. in relazione con altre a. della corteccia;

a. soppressoria, a. che determina inibizione in altre zone della corteccia.