misura

Diritto

M. cautelari

Provvedimenti provvisori e immediatamente esecutivi miranti a evitare che il trascorrere del tempo possa provocare un pericolo per l’accertamento del reato, per l’esecuzione della sentenza ovvero determinare l’aggravamento delle conseguenze del reato o l’agevolazione di altri reati (art. 272-325 c.p.p.; l. 332/1995). Possono essere adottate dall’autorità giudiziaria sia nel corso delle indagini preliminari, sia nella fase processuale, e limitano la libertà personale ovvero la disponibilità di beni. Le m. cautelari si suddividono in: m. cautelari personali e reali. Le prime si distinguono in coercitive e interdittive.

Le m. cautelari personali consistono in limitazioni della libertà personale; sono disposte da un giudice nella fase delle indagini preliminari o nella fase processuale. Per la loro applicazione richiedono l’esistenza di due ordini di requisiti: la sussistenza di gravi indizi di colpevolezza (art. 273, co. 1, c.p.p.), e quella di esigenze cautelari (art. 274 c.p.p.). Per quanto riguarda i criteri di scelta delle m., il giudice tiene conto dell’idoneità di ciascuna in relazione alle esigenze cautelari da soddisfare. Inoltre, devono essere osservati: il principio di adeguatezza, secondo cui la m. della custodia cautelare in carcere deve essere utilizzata solo come extrema ratio, cioè quando le altre risultino inadeguate (tranne i reati di associazione di tipo mafioso, in cui essa è obbligatoria); e il principio di proporzionalità, secondo cui la m. utilizzata deve essere proporzionata al fatto e alla sanzione. Con riferimento alle m. cautelari personali coercitive l’art. 280 c.p.p. stabilisce le loro condizioni di applicabilità disponendo che «salvo quanto disposto dai commi 2 e 3 del presente articolo e dall’art. 391», esse possono essere applicate «solo quando si procede per delitti per i quali la legge stabilisce la pena dell’ergastolo o della reclusione superiore nel massimo a tre anni», e che la custodia cautelare in carcere «può essere disposta solo per delitti, consumati o tentati, per i quali sia prevista la pena della reclusione non inferiore nel massimo a quattro anni», precisando inoltre che «la disposizione di cui al comma 2 non si applica nei confronti di chi abbia trasgredito alle prescrizioni inerenti a una m. cautelare». Questa classe di m. comprende il divieto di espatrio, l’obbligo di presentazione alla polizia giudiziaria, l’allontanamento dalla casa familiare, il divieto o l’obbligo di dimora, gli arresti domiciliari, la custodia cautelare in carcere e la custodia cautelare in luogo di cura.

Le m. cautelari personali interdittive sono provvedimenti adottati dal giudice penale, che limitano temporaneamente l’esercizio di determinate facoltà o diritti, in tutto o in parte. Salvo quanto previsto da disposizioni particolari, possono essere applicate solo quando si procede per delitti per i quali la legge stabilisce la pena dell’ergastolo o della reclusione superiore nel massimo a tre anni (art. 287 c.p.p.). Esse sono: la sospensione dell’esercizio della potestà dei genitori, la sospensione dall’esercizio di un pubblico ufficio o servizio, il divieto temporaneo di esercitare determinate attività professionali o imprenditoriali.

Le misuram. cautelari reali sono, invece, provvedimenti giudiziali che incidono su beni patrimoniali. Sono distinte in due tipologie: il sequestro conservativo e il sequestro preventivo. Il fine comune è garantire l’esecuzione della sentenza definitiva o impedire che l’uso di una cosa pertinente al reato possa agevolare le conseguenze di esso o la commissione di altri reati. Possono essere applicate indipendentemente dalla custodia cautelare in carcere. I provvedimenti concernenti le misure cautelari sono impugnabili.

M. di prevenzione

Denominate anche m. di polizia, sono adottate in base a meri indizi o sospetti. Consistono, infatti, in m. sanzionatorie dirette a evitare la commissione di reati da parte di soggetti considerati socialmente pericolosi. A differenza delle m. di sicurezza non presuppongono la commissione di un reato ma hanno lo scopo di prevenirlo, arginando la pericolosità sociale di determinate categorie di individui; per la loro applicazione è sufficiente la semplice esistenza di un indizio a carico del soggetto. Anche tali m. si distinguono in personali e reali.

Le m. di prevenzione personali sono l’avviso orale, il rimpatrio con foglio di via obbligatorio, la sorveglianza speciale, il divieto e l’obbligo di soggiorno. Le m. di prevenzione reali (o patrimoniali), dirette a colpire i cespiti che si abbia motivo di ritenere essere il frutto o il reimpiego di attività illecite, sono state introdotte dalla l. 646/1982 in ragione della loro particolare idoneità a contrastare le organizzazioni mafiose e il fenomeno dell’usura. Esse sono il sequestro anticipato, il sequestro disposto nel corso del procedimento finalizzato all’applicazione della m. di prevenzione, la confisca e la cauzione.

M. di sicurezza e m. alternative alla detenzione

Le m. di sicurezza sono disciplinate dall'art. 25 Cost. e dall'art. 199 ss. c.p. Principio fondamentale in materia è che nessuno può essere sottoposto a tali provvedimenti se non nei casi espressamente previsti dalla legge.

Presupposti per la loro applicazione sono la commissione di un reato e la pericolosità sociale del suo autore.

Le m. alternative alla detenzione (l. 354/1975) consistono in modalità di esecuzione delle condanne alternative rispetto alla tradizionale esecuzione negli istituti penitenziari. La competenza a decidere sulla loro concessione è affidata al Tribunale di sorveglianza. Possono accedervi i detenuti che hanno evidenziato progressi nel processo di risocializzazione e devono scontare un residuo di pena che risulta nei limiti fissati dalla legge.

Fisica

Il valore di una grandezza, espresso come rapporto tra la grandezza data e un’altra grandezza della stessa specie assunta come grandezza campione o grandezza unitaria (e detta in tal senso unità di m.) e determinato mediante un appropriato metodo di misurazione.

Una grandezza fisica è completamente definita quando ne siano fissate le modalità di misurazione (definizione operativa di grandezza fisica), cioè quando siano fissati i criteri e le procedure mediante i quali è possibile associare a una data grandezza un numero che ne esprima la misura. Per eseguire la misurazione di una classe (o specie) di grandezze omogenee è necessario definire (teoria della m. di Euclide): il criterio di uguaglianza; l’operazione di somma; il campione (o unità di m.). Queste definizioni debbono effettivamente consentire nella pratica la verifica dell’uguaglianza, l’esecuzione della somma, la riproduzione del campione. Conviene definire l’uguaglianza e la somma in modo che godano delle proprietà fondamentali delle corrispondenti relazione e operazione tra numeri, di modo che una generica grandezza della classe possa essere rappresentata con un simbolo letterale e trattata come un’ordinaria variabile algebrica reale. La misurazione di una grandezza fornisce non un ben preciso valore numerico, ma piuttosto un intervallo di valori numerici, originati dagli inevitabili errori che accompagnano la misurazione stessa: ciò comporta che la m. di una grandezza fisica è espressa da un numero e da un errore che rappresentano rispettivamente il valore centrale e la semiampiezza della fascia (➔ errore).

Nella fisica classica si ammette che sia possibile, adottando opportune precauzioni, ridurre quanto si voglia la perturbazione che accompagna l’osservazione dei fenomeni. Il processo di misurazione non pone in questo caso particolari problemi alla teoria; esso può in ultima analisi essere ridotto a un problema essenzialmente tecnico, quello cioè di individuare, per una data grandezza, il processo che apporti al sistema osservato una perturbazione non superiore a un certo limite fissato. Alle grandezze classiche si può pertanto attribuire un carattere obiettivo: si può cioè pensare che, per ogni grandezza fisica di un dato sistema, un particolare valore fra tutti quelli possibili sia obiettivamente realizzato, indipendentemente dal fatto che noi ne siamo a conoscenza oppure no. È così possibile scegliere un certo numero di grandezze fisiche tali che dalla loro conoscenza risulti univocamente individuato il risultato di tutte le misurazioni che si possono eseguire sul sistema: il complesso di dette grandezze fisiche fissa cioè lo stato del sistema. È anche evidente, da quanto detto, che nella fisica classica la conoscenza dello stato del sistema comporta un’informazione completa sul sistema stesso.

Al contrario della fisica classica, quella quantistica introduce, come conseguenza del principio d’indeterminazione di Heisenberg, un estremo inferiore per la perturbazione inerente alla nostra osservazione dei fenomeni e quindi nella misurazione delle grandezze fisiche. Pertanto ogni misurazione fornisce una certa informazione attinente alla grandezza osservata, ma distrugge in generale una certa quantità d’informazione attinente ad altre grandezze, che poteva essere stata raccolta in precedenza. L’informazione completa del sistema diventa così irraggiungibile: avendo eseguito una misurazione di una grandezza e avendo ottenuto un certo valore, è possibile pensare che quel valore sia obiettivamente realizzato nel sistema ma solo al prezzo che, per talune altre grandezze, nessun valore è più sicuramente realizzabile. Con ciò nella meccanica quantistica il concetto d’informazione completa risulta sprovvisto di senso fisico. In sua vece s’introduce il concetto d’informazione massima su un sistema, consistente nella conoscenza esatta del valore numerico del maggior numero possibile di osservabili tra loro indipendenti e tra loro compatibili. È attraverso un’osservazione massima che lo stato del sistema viene, nella teoria quantistica, a essere determinato e quindi noto.

Linguistica

Complemento di m. Indica in quale misura una persona o cosa differisce da un’altra; risponde alla domanda quanto? o di quanto?, ed è in genere costituito da avverbi di quantità e da espressioni quantitative (es.: «è molto più giovane di me»).

Matematica

Generalità

M. di una grandezza A (segmento, area piana, volume, angolo ecc.) rispetto a una grandezza con essa omogenea, U, presa come campione (unità di m.) è il numero reale esprimente il valore del rapporto A:U. Quando si considerino più grandezze omogenee A, B, ... e le loro m. a, b, ... rispetto alla medesima unità, le principali operazioni tra grandezze (somma, differenza ecc.) si traducono nelle operazioni analoghe tra le rispettive m.; per es., la m. della somma A+B di due segmenti, o di due angoli ecc. è la somma a+b delle m. degli addendi. La suddetta proprietà consente di trattare con i metodi dell’algebra le relazioni tra grandezze, sostituendo ciascuna di esse con la sua misura. In alcuni casi conviene considerare anche una m. algebrica, cioè una m. dotata di segno, laddove si voglia tener conto anche di un orientamento: così per la m. di segmenti sopra una retta orientata, o per la m. di angoli tra rette di un fascio orientato ecc.

M. secondo Peano-Jordan e Lebesgue

fig. 1

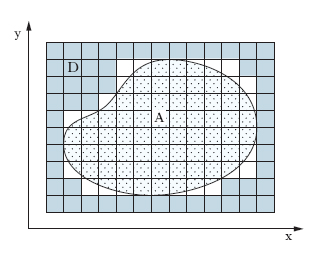
Il concetto elementare di m. si estende, nelle matematiche superiori, a enti più generali e a casi più generali. Quando si consideri un insieme limitato A, sopra una retta, nel piano (come in fig. 1), nello spazio o in un iperspazio, si procede nel modo seguente: fissato uno dei domini rettangolari D contenenti A, lo si decomponga in domini rettangolari parziali e si consideri la somma delle estensioni di quelli che contengono almeno un punto di A (si ricordi che estensione di un dominio rettangolare è il prodotto delle sue dimensioni); quando si fanno tendere a zero le dimensioni di tali domini rettangolari (e quindi all’infinito il loro numero), tale somma tende a una quantità ben determinata, che risulta indipendente dagli elementi arbitrari che intervengono nel procedimento precedente e che si chiama m. esterna di A e si indica con m_eA. In modo analogo si definisce la m. interna di A, che si indica con m_iA; questa si definisce come la differenza tra l’estensione di D e la m. esterna del complementare di A in D. Risulta sempre m_iA≤m_eA; quando sia m_iA=m_eA il loro comune valore si assume come m. secondo Peano-Jordan dell’insieme A, e A stesso si dice misurabile secondo Peano-Jordan. Se l’insieme A è illimitato, esso si dice misurabile se lo sono tutte le sue intersezioni con i domini rettangolari dello spazio ambiente; e per m. di A s’intende l’estremo superiore (eventualmente, ma non necessariamente, infinito) delle m. di tali intersezioni. Nei casi più semplici, come per un segmento rettilineo, per una porzione di piano o di spazio, la m. assume nomi particolari, quali lunghezza, area, volume. A titolo di esempio, la regione del piano limitata dall’asse x, dalla retta x=1, e dalla curva y=1/x è misurabile e ha m. infinita; invece, la regione limitata dall’asse x, dalla retta x=1 e dalla curva y=1/x², pur estendendosi all’infinito, ha m. finita pari a 1.

La definizione di m. secondo Peano-Jordan, sebbene abbastanza generale, non resse a lungo alle critiche, anche perché si costruirono subito insiemi non misurabili in questa accezione. Dopo un tentativo di perfezionamento dovuto a E. Borel, si giunse infine alla definizione di H. Lebesgue (1902), la quale si impose subito dal punto di vista sia teorico sia applicativo. Sempre nel caso che A sia limitato, si considerino tutti gli insiemi aperti e limitati E contenenti A e le loro m. interne m_iE nella accezione precedente; si assume come m. esterna, μ_eA, secondo Lebesgue dell’insieme A l’estremo inferiore dell’insieme numerico descritto da m_iE al variare di E nel modo anzidetto; la m. interna μ_iA si ottiene in modo analogo come estremo superiore delle m_eC, essendo C un qualunque insieme chiuso contenuto in A. Anche qui risulta μ_iA≤μ_eA e quando μ_iA=μ_eA l’insieme A si dice misurabile secondo Lebesgue. Analogamente si procede se l’insieme A è illimitato. Per avere un’idea della grande generalità di tale definizione ricorderemo che si è riusciti a costruire insiemi non misurabili secondo Lebesgue soltanto facendo ricorso al postulato di Zermelo delle infinite scelte arbitrarie.

Le generalizzazioni a spazi più astratti di Rⁿ della teoria della m. di Lebesgue hanno assunto un’importanza crescente per le loro applicazioni in svariati campi (fisica, matematica finanziaria, teoria dell’informazione ecc.). Ricordiamo dunque alcuni elementi fondamentali di questa teoria. Dato un insieme E, una σ-algebra Σ su E è una classe di parti di E alla quale appartenga l’insieme E stesso e che sia stabile per le operazioni di passaggio al complementare e di unione numerabile di parti. Una funzione μ da Σ nell’intervallo [0,+∞] è detta numerabilmente additiva se μ(∅)=0 e μ(A)=Σ_iμ(A_i) per ogni elemento A di Σ e per ogni partizione numerabile (A_i) di A costituita da elementi di Σ. Uno spazio misurabile è una coppia (E, Σ) costituita da un insieme E e da una σ-algebra Σ su di esso. Gli elementi di Σ sono detti insiemi misurabili di E. Una m. sullo spazio misurabile (E, Σ) è una funzione numerabilmente additiva μ su Σ. La terna (E, Σ, μ) è detta spazio misurato o, impropriamente, misurabile. L’additività numerabile della misura μ implica che se A⊆B, allora μ(A)≤μ(B). Si può mostrare che la m. di Lebesgue sul piano è la terna (E, Σ, μ), con E=R², Σ costituita dalla più piccola σ-algebra contenente tutti i rettangoli con i lati paralleli agli assi (detta anche σ-algebra boreliana del piano) e μ definita in modo ‘tradizionale’ sui rettangoli (la misura di un rettangolo è la sua area) e attraverso l’additività numerabile sugli altri elementi di Σ. Si può dimostrare che la σ-algebra boreliana del piano contiene tutte le figure classiche della geometria elementare. La definizione suddetta di spazio misurato e di m. si utilizza in particolare, quando si ponga μ(E)=1, nella teoria della probabilità.

M. invariante di un processo stocastico

Dato un processo stocastico x_t, esso è detto stazionario se, per ogni insieme A, la probabilità P(x_t∈A)=P(A) non dipende da t. La m. di probabilità P(A) definita sugli insiemi A nel modo suddetto è detta appunto m. invariante del processo x_t.

Tecnica

In senso strettamente tecnico, misurazione è l’operazione consistente nel confrontare, direttamente o indirettamente, una certa grandezza fisica con la sua unità di m. allo scopo di determinare la m. della grandezza stessa.

Metodi di misurazione

In generale, esistono due possibili modi di determinare la m. di una grandezza. Il primo consiste nel confrontare la grandezza data con un’altra grandezza omogenea di valore noto (campione), che può essere, in particolare, l’unità di m.: la misurazione si dice allora diretta o relativa (in quanto relativa al campione adottato), e così la m. ottenuta. Il secondo è applicabile a quelle grandezze fisiche che siano esprimibili in funzione di altre grandezze non della stessa specie; dalla misurazione diretta di queste ultime si può ricavare la m. delle prime: la misurazione, e così la m. ottenuta, si dice allora indiretta o derivata, o assoluta (quando ricondotta alla misurazione diretta di grandezze fondamentali del sistema di unità utilizzato). Per es., la velocità media v di un mobile è il rapporto v=s/t fra lo spazio percorso s e il tempo t impiegato a percorrerlo: misurando direttamente s e t si esegue al tempo stesso una misurazione indiretta di v. Una misurazione diretta può effettuarsi in più modi, che differiscono tra loro essenzialmente nel metodo adottato per confrontare la grandezza data con il campione; essa si esegue mediante dispositivi detti genericamente strumenti di m. (o misuratori).

Si distinguono i seguenti metodi fondamentali di misurazione: metodo di sostituzione, consiste nel confrontare l’effetto provocato nel dispositivo di misurazione dalla grandezza data con quello provocato dal campione; metodo di compensazione o di opposizione o di azzeramento o di zero, deriva dal precedente, ma, a differenza di questo, la grandezza da misurare e il campione sono introdotti contemporaneamente nel dispositivo di misurazione, in modo tale che i loro effetti si elidano reciprocamente; è un metodo largamente usato per misurazioni di grande precisione (potenziometri, ponti di m. ecc.); metodo degli strumenti tarati, a differenza dei metodi precedenti, nei quali la grandezza viene ogni volta confrontata con il campione che, pertanto, deve essere sempre disponibile, in questo metodo la grandezza da misurare agisce su uno strumento tarato, sul quale cioè sono stati fatti agire preventivamente campioni di valore opportuno, per cui le indicazioni dello strumento sono direttamente convertibili in valori della grandezza misurata; spesso la scala dell’indicatore dello strumento è già graduata in multipli e sottomultipli dell’unità di m., e la misurazione si dice allora a lettura diretta (calibro, termometro ecc.).

Apparati di misurazione

Ogni operazione di misurazione può considerarsi come l’insieme di tre distinte operazioni, ciascuna delle quali viene realizzata mediante uno (o più) dispositivi, incorporati o meno in uno stesso strumento. La prima fase è quella nella quale la grandezza da misurare viene sentita e, generalmente, trasdotta in un’altra di specie diversa; il dispositivo apposito si dice sensore (o trasduttore). La seconda fase è quella in cui la grandezza viene elaborata, in particolare, filtrata, amplificata, derivata, integrata ecc.; il dispositivo apposito si dice elaboratore (o condizionatore). La terza fase è quella in cui la grandezza viene presentata all’occhio dell’osservatore; il dispositivo apposito si dice indicatore (o visualizzatore o terminale). La possibilità di individuare in ogni misurazione tre fasi, e di far loro corrispondere tre dispositivi diversi, consente di utilizzare gli stessi dispositivi per misurare grandezze diverse: ciò significa, più precisamente, che mentre per ogni grandezza occorre un apposito sensore (per es., una termocoppia per misurare una temperatura, un estensimetro per misurare una deformazione ecc.), l’elaborazione e la presentazione della misurazione possono essere svolte da filtri, amplificatori ecc., dello stesso tipo, e quindi intercambiabili, ovvero da voltmetri, oscilloscopi ecc., ancora intercambiabili.

fig. 2

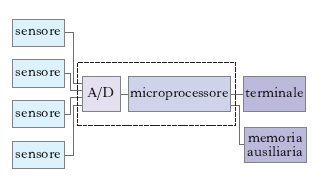
Lo sviluppo dei microprocessori permette ormai di realizzare apparati di misurazione digitali. In tal caso il sistema di misurazione si specializza come in fig. 2: in essa le grandezze in uscita dai vari sensori, ottenute sotto forma analogica, applicate a un convertitore analogico digitale (A/D in fig.), vengono convertite in forma digitale e inviate al microprocessore che ne esegue l’acquisizione e l’elaborazione; come terzo stadio, oltre al terminale di presentazione può essere presente un dispositivo di memoria ausiliaria.

Approfondimenti di attualità

Imputato alloglotta e traduzione dell'ordinanza cautelare ex artt. 27 c.p.p. di Sabino Morisco

Due sentenze delle sezioni unite in tema di misure cautelari di Giorgio Spangher