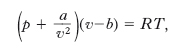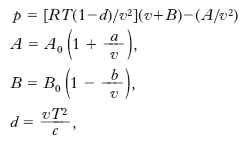stato

Diritto

S. civile

È il complesso delle singole posizioni giuridiche spettanti alla persona nella famiglia, nello Stato e nella comunità giuridica. Fin dalle origini dello Stato moderno gli atti dello s. civile rispondono all’esigenza di documentare pubblicamente fatti influenti sullo s. delle persone: nascita, matrimonio, morte, cittadinanza. Tale documentazione è, perciò, precostituita a cura di un funzionario pubblico, l’ufficiale dello s. civile. Ogni comune ha un ufficio dello s. civile (art. 1 d.p.r. 396/2000). Ufficiale dello s. civile è il sindaco, nonché i dipendenti a tempo indeterminato (e, in caso di esigenze straordinarie e temporalmente limitate, a tempo determinato: art. 2 d.p.r. 79/2009) del comune, ai quali siano state delegate le funzioni di ufficiale di s. civile. Negli atti dello s. civile, oltre all’iscrizione delle dichiarazioni rese direttamente all’ufficiale di s. civile e alla trascrizione di atti ricevuti da altri pubblici ufficiali, si procede all’annotazione di atti successivi alla prima iscrizione, in modo da integrare la pubblicità realizzata in via principale con l’iscrizione e la trascrizione. Gli ufficiali dello s. civile devono rilasciare gli estratti e i certificati che vengano loro domandati con le indicazioni dalla legge prescritte (art. 450 c.c.). Gli estratti degli atti dello s. civile possono essere rilasciati per riassunto, riportando le indicazioni contenute nell’atto stesso e nelle relative annotazioni, ovvero per copia integrale; in quest’ultimo caso, soltanto quando ne è fatta espressa richiesta da chi vi ha interesse e il rilascio non è vietato dalla legge. Gli atti dello s. civile fanno prova, fino a querela di falso, di ciò che l’ufficiale pubblico attesta essere avvenuto alla sua presenza o da lui compiuto (art. 451 c.c.). Chi intende promuovere la rettificazione di un atto dello s. civile o la ricostituzione di un atto smarrito o la formazione di un atto indebitamente registrato, deve proporre ricorso al tribunale, che provvede in camera di consiglio con decreto motivato.

S. di necessità

In diritto penale, lo s. di necessità è la condizione in cui si trova chi compie un fatto dannoso perché costrettovi dalla necessità di salvare sé o altri dal pericolo attuale di un danno grave alla persona, senza che il pericolo sia stato da lui volontariamente causato né fosse altrimenti evitabile. Sempre che il fatto sia proporzionato al pericolo, lo s. di necessità esclude la responsabilità penale, salvo che il fatto sia stato commesso da chi ha un particolare dovere giuridico di esporsi al pericolo. Si distingue dalla legittima difesa poiché, in questa, soggetto passivo dell’azione è chi ha messo in pericolo, mediante una offesa ingiusta, il diritto difeso, mentre nello s. di necessità l’azione colpisce un soggetto che può anche non aver concorso a provocare o a determinare il pericolo. La discriminante non si applica se lo s. di necessità è determinato dall’altrui minaccia; ma, in tal caso, del fatto commesso dalla persona minacciata risponde chi l’ha costretta a commetterlo (art. 54 c.p.).

In diritto civile, colui che ha cagionato un danno in s. di necessità è obbligato a pagare al danneggiato un’indennità la cui misura è rimessa all’equo apprezzamento del giudice (art. 2045 c.c.). Di s. di necessità si parla anche nel caso in cui il mancato adempimento di una obbligazione sia stato determinato dalla necessità d’evitare a sé stesso un danno patrimoniale. In tal senso lo stato di necessità rimane un fatto interno del debitore e non può essere considerato causa a lui non imputabile.

Economia

Nel linguaggio commerciale e contabile, con opportune qualificazioni, il documento, il prospetto, la relazione da cui risulta una particolare situazione economica, amministrativa ecc. S. di previsione Documento contabile che espone la previsione di un’intera gestione economica o finanziaria di un’azienda o di alcune operazioni di questa (nel bilancio dello Stato, è il documento da cui risultano le spese o le entrate previste dello Stato; c’è uno s. di previsione generale di tutte le entrate e inoltre uno s. di previsione delle spese per ciascun ministero). S. di liquidazione Esposizione dei rapporti patrimoniali da sistemare o risolvere, oppure dei valori di realizzo di singoli beni o di complessi patrimoniali. S. mensile di borsa Lo s. di liquidazione che a fine mese l’associato alla stanza di compensazione deve esibire alla stessa per la liquidazione dei contratti di borsa in scadenza, in modo che si possa determinare la posizione debitoria o creditoria dell’associato in titoli e in contante S. patrimoniale Prospetto nel quale vengono rappresentati gli elementi attivi e passivi del patrimonio di un’azienda. S. di avanzamento Documento richiesto da enti pubblici o privati per la liquidazione di quanto dovuto per lavori in appalto il cui pagamento debba eseguirsi in più volte durante la loro esecuzione, oppure da banche per la liquidazione delle quote di mutuo edilizio da somministrare durante l’avanzamento dei lavori di costruzione. S. finale Qualsiasi s. di liquidazione redatto alla fine della liquidazione medesima oppure uno s. patrimoniale compilato a fine esercizio.

Fisica e chimica

In fisica e in chimica e anche nella tecnica, condizione nella quale si trova una sostanza, un sistema materiale, un corpo, cioè condizione particolare individuata da un determinato numero di parametri.

Definizioni

Si parla di s. meccanico o di s. di moto con riferimento ai valori istantanei delle coordinate spaziali e delle componenti del vettore velocità, di s. termodinamico, con riferimento ai valori di equilibrio dei parametri di s., ossia dei parametri che individuano lo s. di equilibrio del sistema, in particolare, la pressione e la temperatura; si parla inoltre di grandezza (o funzione) di s., con riferimento a una grandezza fisica, come l’energia interna, l’entropia, l’entalpia ecc., dipendente solo dallo s. di un sistema. Il diagramma di s. è la rappresentazione grafica dei valori dei parametri di s. di un sistema termodinamico ai quali corrispondono s. di equilibrio in cui possono coesistere due o più fasi (➔ diagramma). Lo s. nullo (o s. zero) di un sistema termodinamico è lo s. convenzionalmente assunto come riferimento. Lo s. critico è quello di un sistema nelle condizioni per le quali sia possibile lo stabilirsi di un particolare fenomeno: per es., nel caso di un materiale fissile si parla di s. critico quando il numero di neutroni prodotto per fissione nell’unità di tempo uguaglia quello dei neutroni assorbiti o perduti dal materiale. In meccanica quantistica lo s. puro è la condizione di un sistema sul quale si ha la massima informazione compatibile con i principi della meccanica quantistica: tale informazione è fornita dai valori assunti sullo s. da un insieme di osservabili, tra loro commutanti, che risulti completo, cioè tale che a un dato insieme di autovalori corrisponda un unico s. fisico; la misurazione contemporanea di osservabili compatibili è detta anche preparazione dello stato. Se le osservabili misurate costituiscono un insieme completo, lo s. del sistema è descritto, a meno di una costante moltiplicativa, da un unico vettore dello spazio di Hilbert degli s. (➔ spazio); nel caso contrario il sistema è detto trovarsi in uno s. misto, la cui descrizione si effettua attraverso la matrice densità o matrice statistica (➔ statistico). Lo s. stazionario è la condizione di un sistema descritta da parametri che non dipendono dal tempo. Gli s. di aggregazione rappresentano i modi diversi (s. liquido, s. solido, s. gassoso) nei quali possono trovarsi associate le molecole, gli atomi o gli ioni d’una sostanza (➔ aggregazione); la materia si presenta anche allo s. di plasma (➔). Con significato specifico, si parla di s. di elettrizzazione (o elettrizzato), di magnetizzazione, di polarizzazione magnetica, dielettrica, di un corpo; di s. di tensione di una struttura ecc. Lo s. energetico è quello caratterizzato da un determinato valore dell’energia totale di un corpo (s. energetici atomici, elettronici ecc.); in particolare, la determinazione degli s. energetici accessibili a un sistema quantistico si ottiene risolvendo la relativa equazione di Schrödinger, e le autofunzioni così ottenute descrivono s. che risultano stazionari; lo s. eccitato è lo s. energetico nel quale un sistema si porta per apporto di energia dall’esterno e dal quale ritorna poi, emettendo il sovrappiù di energia, nello s. fondamentale di partenza.

Lo s. igrometrico dell’aria indica le condizioni di umidità relativa dell’aria in un determinato posto.

La locuzione allo s. nativo si riferisce a elementi chimici che si trovino in natura allo s. non combinato (come l’oro, il rame, lo zolfo ecc.); allo s. nascente si riferisce a specie chimiche al momento del loro sviluppo in seguito a una reazione.

Lo s. risonante, in fisica nucleare, è lo stesso che risonanza (➔).

Lo s. vetroso è lo s. di aggregazione della materia analogo a quello tipico del vetro (➔).

Equazioni di stato

Si dicono equazioni di s. quelle che stabiliscono una correlazione fra le grandezze individuanti lo s. di un sistema. Le equazioni di s. di sostanze specifiche non sono ricavabili nell’ambito della termodinamica, poiché essa fornisce relazioni generali indipendenti dalle proprietà specifiche dei vari sistemi. La meccanica statistica, facendo intervenire la struttura microscopica della materia, permette invece di dedurre relazioni tra proprietà termodinamiche e grandezze microscopiche, che consentono, in linea di principio e almeno in casi semplici, di calcolare l’equazione di s. a partire da principi primi. In genere si adottano come grandezze di riferimento quelle più facilmente determinabili, quali pressione p, volume molare v e temperatura T, come nel caso dei gas (➔) perfetti.

Per i gas reali, le più di 100 equazioni di s. proposte descrivono il comportamento del sistema rappresentato tanto meglio quanto maggiore è la loro complessità, cioè il numero delle costanti. Fra le equazioni a due costanti (a e b), ricordiamo: l’equazione di van der Waals

essendo R la costante dei gas, e l’equazione di Redlich-Kwong

dove le due costanti a e b sono calcolabili in funzione della temperatura critica, Tc, e della pressione critica pc. Fra le equazioni a maggior numero di costanti, ricordiamo l’equazione di Clausius, che contiene 5 costanti, l’equazione di Beattie

dove A0, B0, a, b, c, sono costanti caratteristiche del gas in esame, e l’equazione viriale (➔) di stato.

Per molti gas reali vale il teorema degli s. corrispondenti, per cui gas con uguali valori dei parametri ridotti pr = p/pc) e Tr = T/Tc (il pedice c indica le condizioni critiche) mostrano uguale scostamento dalle condizioni di gas perfetto. Il teorema nasce dalla constatazione sperimentale che le isoterme dei gas reali hanno andamenti simili (e spesso in pratica coincidono) se riportate su diagrammi con coordinate espresse in termini di parametri ridotti. Si può perciò individuare, mediante i parametri ridotti, un’unica equazione di s. generalizzata, priva di costanti specifiche del sistema esaminato. Introducendo nell’equazione di s. dei gas perfetti un fattore di compressibilità z che tenga conto dello scostamento dalle condizioni di idealità (pv = zRT), il teorema degli s. corrispondenti risulta espresso dalla seguente equazione: z = z(pr, Tr), per cui gas reali con uguali valori di pressione e temperatura ridotte hanno uguale fattore di compressibilità. Il teorema degli s. corrispondenti non ha validità generale e presenta in molti casi deviazioni anche notevoli che si possono in parte correggere introducendo nell’equazione di z, oltre a pr e Tr, il fattore di compressibilità zc al punto critico, caratteristico di ogni singolo gas reale. Il teorema degli s. corrispondenti, espresso nella forma z = z(pr, Tr, zc), può essere esteso allo s. liquido, pur con cautele e limitazioni.

Teoria dei sistemi

Nella teoria dei sistemi, il termine s. denota l’insieme delle grandezze caratteristiche di un sistema dinamico, il cui ruolo è quello di riassumere, istante per istante, gli effetti dei valori passati dell’ingresso, così da rendere univoca la determinazione dei valori presenti e futuri dell’uscita del sistema. Lo s. è, in generale, variabile nel tempo e assume valori in un insieme X (spazio di s.). L’associazione di uno spazio di s. X a un sistema, inteso come insieme di tutte le possibili coppie costituite da un ingresso ammissibile e dall’uscita corrispondente, è legata alla possibilità di parametrizzare tali coppie attraverso tutti e soli gli elementi di X, ovvero all’esistenza di due funzioni, η(t, x(t), u(t) (funzione di uscita) e ϕ(t, t0, x0, u) (funzione di transizione dello s.), dotate di opportune proprietà, e in grado di fornire a ogni istante t l’uscita del sistema (in base ai valori attuali dello s. x(t) e dell’ingresso u(t)) e, rispettivamente, lo s. attuale (in funzione dell’istante iniziale t0, dello s. iniziale x0 appartenente a X, e dell’andamento dell’ingresso u dall’istante iniziale a quello di osservazione t). Una terna (X, ϕ, η) con le suddette caratteristiche è detta rappresentazione con lo spazio di s. (o rappresentazione ingresso-s.-uscita) del sistema e la sua esistenza può essere assicurata sotto ipotesi molto generali. D’altra parte si può facilmente mostrare che tale terna non è unica. In particolare, l’esistenza di più rappresentazioni con lo spazio di s. è anche legata alla possibilità di usare uno spazio di s. ridondante per descrivere il sistema. In tal senso, due elementi dello spazio di s. xa e xb si dicono equivalenti a un dato istante t0 se, a partire da x(t0)=xa o da x(t0)=xb si ottengono uscite identiche per qualsiasi ingresso applicato. Una rappresentazione che a ogni istante non ha s. equivalenti è detta minima.

La rappresentazione costituita da una terna (X, ϕ, η) consente di calcolare lo s. assunto dal sistema in un qualsiasi istante di tempo t in modo esplicito, cioè come valore della funzione ϕ ed è per questo detta rappresentazione in forma esplicita. Accanto a questa, si considera spesso una rappresentazione in forma implicita, in cui l’evoluzione dello s. è descritta da un’equazione differenziale che deve essere integrata a partire dalla condizione iniziale x(t0)=x0, al fine di conoscere il valore dello s. in un particolare istante t. Per sistemi a tempo continuo, la forma implicita di una rappresentazione con lo spazio di s. esiste se e solo se la funzione ϕ è derivabile rispetto all’argomento t, e in tal caso la rappresentazione è detta regolare. Ulteriori classificazioni delle rappresentazioni con lo spazio di s. possono essere fatte in base a corrispondenti proprietà delle funzioni ϕ ed η e alla scrittura degli insiemi X, U (insieme dei valori di ingresso), Y (insieme dei valori di uscita), e U (insieme delle funzioni di ingresso). In particolare, una rappresentazione con lo spazio di s. è detta a dimensione finita se X, U ed Y ammettono una struttura di spazio lineare e hanno ciascuno dimensione finita. È detta stazionaria, se l’insieme Ʋ è chiuso rispetto alla traslazione, se la funzione di uscita η non dipende esplicitamente dal tempo e se la funzione di transizione dello s. ϕ dipende dal tempo solo attraverso la quantità (t−t0) (tempo trascorso dall’istante iniziale di applicazione dell’ingresso). Infine una rappresentazione con lo spazio di s. è detta lineare se gli insiemi X, U, Y e U hanno una struttura di spazio lineare e se, per ogni istante iniziale t0 e istante di tempo t, le funzioni ϕ ed η sono lineari negli altri argomenti, ovvero s. iniziale x0 e funzione di ingresso u per la ϕ, e s. e ingresso attuali, x(t) e u(t), per la η. Le rappresentazioni lineari godono naturalmente di notevole interesse, sia per l’ampia classe di sistemi che descrivono, sia per le semplificazioni analitiche che hanno consentito lo sviluppo di un’estesa e consolidata teoria in quest’ambito.

Psicologia

S. secondo Condizione abnorme che nella sua forma genuina è un restringimento più o meno grave della coscienza, in cui un soggetto compie azioni in apparenza coordinate e complesse, senza serbarne ricordo. Nelle analoghe manifestazioni di alcuni psicopatici si osserva spesso, oltre ai disturbi della memoria, anche un netto contrasto tra le abitudini del soggetto e le azioni compiute in tali condizioni, tanto da suggerire una corrispondenza tra s. secondi e un disturbo dell’intera personalità, come se quella abituale venisse sopraffatta dall’irruzione di una personalità differente (sdoppiamento della personalità o personalità alternante).