liquido

Fisica

Lo stato l. è quello stato di aggregazione della materia nel quale una sostanza ha volume ben determinato e pressoché invariabile per qualunque valore della pressione, ma non ha forma propria, e assume perciò quella del recipiente che la contiene.

Caratteri generali

La capacità di un l. di assumere la forma del recipiente in cui viene posto, o più precisamente l’incapacità di sopportare sforzi di taglio statici, è dovuta all’estrema scorrevolezza reciproca delle sue particelle. Tale scorrevolezza è dovuta al fatto che fra particella e particella sono modesti gli sforzi tangenziali, o attriti interni, cioè la viscosità assume in genere valori abbastanza piccoli. La compressibilità e la dilatabilità hanno nei l. entità minima: per la maggior parte dei l. la variazione relativa del volume è di pochi centomillesimi sotto un incremento di pressione di 10⁵ Pa e aumenta di pochi decimillesimi per un aumento di temperatura di 1 °C; il coefficiente di viscosità varia, nel SI, da pochi decimi di Pa∙s per i l. più viscosi (tipo glicerina) a qualche millesimo di Pa∙s per i l. più scorrevoli (tipo acqua).

Dove tale entità si supponga addirittura nulla, si ha un modello ideale di l.: il l. perfetto (fluido, non viscoso, incompressibile, indilatabile) di cui ci si serve, finché è possibile, per la trattazione matematica dei problemi inerenti ai liquidi. In un l. perfetto (in generale, in un fluido perfetto), intorno a un suo punto qualunque, la pressione è la stessa in tutte le direzioni: tale proprietà, stabilita in via teorica da A.-L. Cauchy, trova conferma nel principio sperimentale di B. Pascal.

Per i l. reali la tensione tangenziale (o sforzo di taglio) τ  che nasce per effetto di una differenza dv  di velocità fra due strati contigui distanti dx  è funzione del gradiente di velocità dv/dx. In molti casi tale relazione funzionale è di semplice proporzionalità:

dove μ è detto viscosità assoluta (o coefficiente dinamico di viscosità). Se μ si mantiene costante al variare dell’entità e del tempo di applicazione dello sforzo di taglio, si parla di l. newtoniani; se μ varia con l’entità dello sforzo di taglio o con il tempo di applicazione dello sforzo, si parla di l. non newtoniani.

Il passaggio dallo stato l. allo stato solido si chiama solidificazione; il passaggio inverso fusione; il passaggio dallo stato aeriforme a quello l. è detto liquefazione (o, in particolare, condensazione), l’inverso evaporazione (o, in speciali condizioni, ebollizione).

Proprietà microscopiche dello stato liquido

La definizione di stato l. come quello stato di aggregazione della materia che presenta volume definito ma che non ha forma propria, pur essendo in generale utilizzabile nella pratica, risulta insoddisfacente se analizzata con cura, perché molti cosiddetti ‘solidi’ si comportano come l. se sottoposti a sforzi sufficientemente intensi. Solo se si passa ad analizzare le proprietà microscopiche dello stato l., questo può essere chiaramente differenziato dal solido cristallino sulla base dell’ordine spaziale delle molecole. Nel processo di fusione si ha infatti una trasformazione durante la quale non variano significativamente né le distanze né le energie d’interazione intermolecolari, mentre si viene a perdere l’ordinamento a grandi distanze proprio della struttura cristallina. Anche se nel passaggio cristallo-l. si hanno in generale insieme perdita di correlazione spaziale e aumento di mobilità, queste proprietà non sono in diretta relazione tra loro; esiste in effetti un’ampia classe di sostanze (stati vetrosi e amorfi) che, pur non possedendo ordinamento cristallino, presentano valori della mobilità molecolare simili a quelli dei cristalli; questi materiali, pur essendo comunemente detti ‘solidi’, dovrebbero in realtà essere considerati l. ad altissima viscosità. La differenza tra l. e amorfi non è qualitativa ma solo quantitativa; considerare il sistema l. o solido amorfo dipende solo dalla scala di tempo nella quale si effettua l’osservazione: i materiali amorfi sottoposti a sollecitazioni di taglio si comportano come l. se si aspetta un tempo sufficientemente lungo; viceversa anche nei l. ordinari si possono osservare modi di vibrazione trasversale, legati all’esistenza di sforzi di taglio, se si considerano oscillazioni con periodi dell’ordine di 10^–11 s.

A seconda delle caratteristiche delle molecole componenti e in particolare del tipo di potenziale intermolecolare si possono distinguere diverse classi di l.: l. molecolari, l. di molecole chimicamente inerti (gas nobili, N₂, I₂ ecc.) che interagiscono solo con forze di dispersione o forze di Van der Waals, cioè interazioni di energia 100 volte inferiore a quella di un vero e proprio legame chimico; l. polari e associati, in questo caso le molecole costituenti posseggono momenti elettrici di elevata intensità o sono capaci d’interagire tramite legami chimici deboli, quale il legame idrogeno: l’acqua appartiene a questa classe; soluzioni o miscele, sistemi nei quali le molecole componenti il l. non sono tutte della stessa specie; metalli l. e l. ionici, l. con forti legami chimici ottenuti dalla fusione dei solidi corrispondenti (normalmente a temperature alte rispetto alla temperatura ambiente). Infine alcuni l., i superfluidi, presentano caratteristiche del tutto particolari, la più vistosa delle quali è la capacità di fluire attraverso capillari senza viscosità; tali proprietà sono connesse a effetti quantistici (➔ superfluidità).

Teorie microscopiche dello stato liquido

Costruire una teoria microscopica dello stato l. significa costruire un modello microscopico che permetta di calcolare la funzione di partizione del sistema, la cui conoscenza consente lo studio del comportamento termodinamico del sistema stesso. Le teorie proposte possono dividersi in due gruppi: le teorie pseudoreticolari e le teorie meccanico-statistiche. Nel primo gruppo sono comprese le teorie dello stato l. che partono da un modello che nelle sue linee essenziali è assimilabile a un modello pseudosolido. Questo punto di vista è dettato dalla constatazione sperimentale che molte proprietà termodinamiche del l. vicino al punto di fusione sono poco diverse da quelle del solido. Questo non è più vero per densità vicine a quella del punto critico, ma lo scopo di queste teorie è di descrivere il l. solo nell’intorno del punto di fusione. Le teorie meccanico-statistiche, sviluppate essenzialmente per i fluidi formati da molecole semplici, si differenziano tra loro per le approssimazioni introdotte nel corso del procedimento.

Metodi di simulazione numerica

Con l’avvento dei calcolatori molto veloci, si è aperto un nuovo campo pseudosperimentale chiamato di simulazione numerica (➔ computazionale), molto utile per lo studio di sistemi a N corpi e in particolare per quello dei liquidi. Vi sono due metodi con cui si possono usare i calcolatori per studiare le proprietà di equilibrio di un liquido: il metodo della dinamica molecolare, che consiste nel seguire nel tempo, risolvendo numericamente l’equazione del moto, l’evoluzione di un determinato numero di molecole (tipicamente alcune centinaia) che interagiscono con un potenziale interatomico, obbediscono alle leggi della meccanica classica e partono con una configurazione scelta a caso; il metodo Montecarlo, che consiste nel generare, con sorteggio di numeri casuali per un certo numero di molecole, una catena di configurazioni aventi frequenza di ricorrenza pari a exp[–βU], dove U è l’energia potenziale del sistema per quella configurazione. Le proprietà di equilibrio si ottengono mediando i valori calcolati per ogni configurazione su tutte le configurazioni della catena. Anche nel metodo Montecarlo il numero di molecole usato è dell’ordine delle centinaia.

La simulazione numerica sembra la tecnica più valida per ottenere informazioni sulla struttura dei liquidi. La situazione della fisica dello stato l. può considerarsi soddisfacente per quanto riguarda lo studio degli stati di equilibrio termodinamico (in particolare per i l. composti da molecole semplici). Un settore nel quale la conoscenza a livello microscopico non ha ancora raggiunto un livello parimenti soddisfacente è quello degli stati di non equilibrio e dei conseguenti fenomeni di rilassamento, tramite i processi di dissipazione; a questo settore è perciò attualmente dedicata gran parte delle ricerche.

Correnti liquide

In idraulica si definisce corrente l. la massa di l. che si muove in una regione di spazio ben determinata (corso d’acqua, canale, condotta ecc.).

Tipi di regimi

Le correnti l. possono essere a regime laminare (o regolare o di Poiseuille) o a regime turbolento: nel primo caso le particelle percorrono traiettorie regolari che non si discostano molto dal percorso della massa l. considerata nel suo insieme; nel secondo invece le particelle, oltre al moto comune di trasporto lungo il corso della corrente, possiedono un movimento vorticoso di notevole contenuto energetico e non seguono più traiettorie regolari. Ci si può tuttavia riferire, in molte trattazioni pratiche, al movimento medio di trasporto, introducendo una velocità (e in genere anche una pressione) media nell’intorno di ciascun punto della corrente in esame.

Generalmente, pressione e velocità variano da punto a punto della corrente, e in ciascun punto variano con il tempo: si parla allora di corrente l. a regime variabile. Può accadere però che, per particolari condizioni, la velocità e la pressione medie, pur variando da punto a punto, siano in ciascun punto costanti nel tempo; la corrente l. si dice allora in regime permanente (o stazionario), mentre si dice in regime uniforme se velocità e pressione medie sono, oltre che costanti nel tempo in ciascun punto, uguali in tutti i punti della corrente. In una corrente a regime variabile le linee di flusso del campo del vettore velocità sono generalmente variabili da istante a istante, e sono distinte dalle traiettorie delle particelle, cioè dalle linee di corrente. In una corrente a regime permanente, invece, le linee di flusso sono invariabili nel tempo e si identificano con le linee di corrente. Il flusso del vettore velocità attraverso una superficie S si chiama portata (si tratta, com’è evidente, di una portata in volume) della corrente attraverso S.

Una corrente l. si dice in pressione o a pelo libero, a seconda che il l. occupi tutta la sezione del condotto in cui si muove, o che solo una parte del contorno della sezione sia rigida e che il l. sia, lungo la parte rimanente del contorno, a contatto con l’aria.

fig. 1A

Correnti l. a pelo libero  

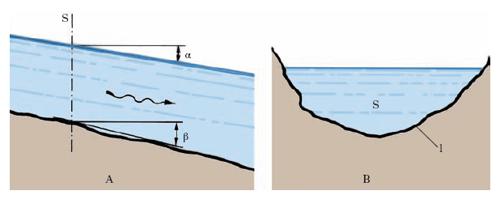
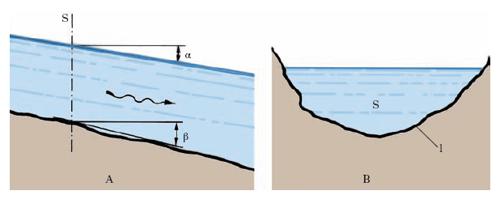
In una sezione verticale s della corrente l. (fig. 1A) i valori medi della pressione variano idrostaticamente. Si chiama pendenza del pelo libero (o pendenza motrice), nella generica sezione trasversale, il seno I dell’angolo α formato dall’orizzontale e dalla tangente al profilo del pelo libero nella sezione stessa; trattandosi normalmente di un angolo molto piccolo, il seno è confondibile con la tangente trigonometrica e questo giustifica la denominazione di pendenza. Si chiama invece pendenza del fondo il seno I_f dell’angolo β formato dall’orizzontale e dalla tangente al profilo del fondo. Raggio medio si dice poi (fig. 1B) il rapporto R tra l’area S della sezione e la lunghezza l del contorno bagnato; portata Q è il volume di l. che nell’unità di tempo attraversa la sezione; velocità media U è il valore medio delle velocità di trasporto nei punti della sezione: si ha evidentemente Q = US. In un moto permanente, U e S possono essere diversi da sezione a sezione, ma la portata Q ha lo stesso valore in tutte le sezioni. In una corrente a regime uniforme che, come si è detto, è un caso particolare di regime permanente, U è la stessa in ogni sezione e costante pertanto deve essere anche la sezione della corrente. Correnti a regime uniforme si hanno, per es., in un alveo a sezione costante e pendenza del fondo anch’essa costante. In tal caso il pelo libero è parallelo al fondo (I = I_f) e si ha U=χ√‾‾‾‾RI (formula di Chézy). Il coefficiente χ, che dipende in larga misura dalla natura delle pareti dell’alveo e, a parità di scabrezza di queste, cresce con il raggio medio, può essere calcolato empiricamente per l’acqua mediante la seconda formula di Bazin che, esprimendo χ e R nel Sistema Internazionale, si scrive: χ=87/(1+γ_b/√‾‾R. I valori del coefficiente γ_b possono variare in pratica da 0,06 per pareti molto lisce a 1,30-1,70 per pareti in terra di media ed elevata resistenza. Le formule del moto uniforme si possono usare non solo quando il moto sia realmente tale, ma anche quando le variazioni di velocità siano molto graduali e lente.

fig. 2

Correnti l. in pressione

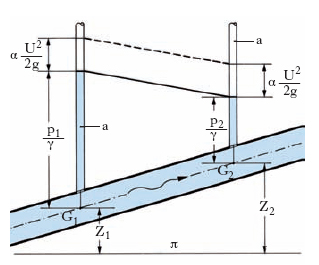
Nei tubi completamente pieni, al disotto di un certo valore della velocità il moto dei l. è laminare. Per valori della velocità superiori a un certo altro valore, il moto è invece sempre turbolento. Questi due valori caratteristici della velocità sono detti rispettivamente: velocità critica inferiore (U_ci) e velocità critica superiore (U_cs). Per valori compresi tra le due velocità critiche si può verificare l’uno o l’altro dei due regimi. Le condotte d’acqua che hanno interesse nella tecnica presentano generalmente regime vorticoso e le circostanze del moto sono in tutto paragonabili a quelle che si verificano nei corsi a pelo libero. Immaginiamo una condotta d’acqua di diametro molto piccolo rispetto alla lunghezza e nella quale regni una pressione maggiore di quella atmosferica (fig. 2). Applicando a una sezione, il cui baricentro G sia a una quota z rispetto a un piano orizzontale di riferimento π, un tubetto verticale a aperto in alto, si constata che l’acqua sale in esso fino a una certa altezza al di sopra del baricentro della sezione. Se p è la pressione che regna nella condotta nel punto d’inserzione del tubetto e γ è la densità dell’acqua, tale altezza risulta pari a p/γ. La quota h=z+p/γ si chiama quota o carico piezometrico della condotta nella sezione considerata. Ripetendo l’indagine per molte sezioni, la linea che congiunge gli estremi superiori delle quote piezometriche si dice linea dei carichi piezometrici o linea piezometrica. Se il moto dell’acqua viene arrestato (per es. chiudendo a valle la condotta), in un tubetto applicato alla generica sezione della condotta il livello dell’acqua sale ancora di αU²/(2g), se U è la velocità che l’acqua aveva prima in quella sezione; α è il coefficiente di Coriolis. La quota z+p/γ+αU²/(2g) si chiama carico effettivo, e linea dei carichi effettivi quella che ha tali quote come ordinate. In condizioni di moto permanente, applicando il teorema di Bernoulli ai vari filetti fluidi della condotta (la quale può considerarsi un tubo di flusso del moto medio di trasporto), si deduce che il carico effettivo si manterrebbe costante lungo l’intera condotta, se non vi fossero dissipazioni di energia. Queste sono in realtà sempre presenti per effetto degli attriti lungo le pareti del tubo oltre che degli attriti interni tra i diversi filetti fluidi. Corrispondentemente la linea dei carichi effettivi subisce un graduale abbassamento procedendo lungo la condotta nel verso del moto dell’acqua. Qualora, più restrittivamente, il moto sia uniforme (cioè permanente e con la stessa velocità in tutte le sezioni) anche la linea piezometrica, dovendo in ogni sezione sottostare alla linea dei carichi di un’altezza costante αU²/(2g), diviene a quella parallela e perciò gradualmente decrescente. La pendenza piezometrica, cioè la pendenza della linea piezometrica, viene a identificarsi in questo caso con il valore della perdita di carico per unità di lunghezza del condotto. Le equazioni del moto sono del tutto analoghe a quelle delle correnti a pelo libero, salvo l’opportuna scelta del coefficiente di scabrezza in base alla natura e allo stato del materiale costituente i tubi.

Linguistica

In fonetica, consonanti l. erano dette dagli antichi (gr. ὑγρὰ στοιχεῖα, lat. liquidae consonantes) le consonanti l, r, m, n per la loro peculiarità metrica di costituire o no posizione dopo una muta; per la linguistica moderna sono liquide solo i vari tipi di l e r. Per le l. sonanti ➔ sonante.

Tecnica

In ingegneria, i dispositivi a l. sono particolari strumenti di misurazione, in cui si sfruttano opportunamente determinate proprietà dei liquidi. Per es., ammortizzatori a l. (o idraulici), in cui si sfruttano la scarsa comprimibilità e la viscosità di un l., oppure termometri a l., in cui si sfrutta la dilatabilità termica di un liquido.