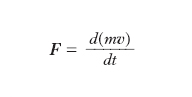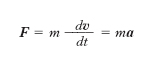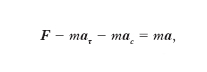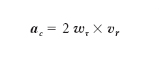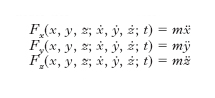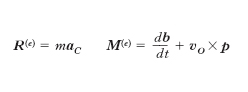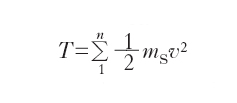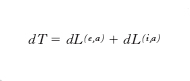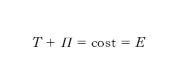dinamica

Chimica

Per la dinamica in chimica ➔ dinamica molecolare.

Economia

Per la dinamica in economia ➔ dinamica economica.

Fisica

Parte della meccanica che studia i movimenti dei corpi in relazione alle cause che li determinano. Nella dinamica si può far rientrare la statica, considerando la quiete come un aspetto particolare del moto.

Cenni storici

Se a I. Newton spetta il merito di aver stabilito le leggi fondamentali della meccanica, è Galileo che deve considerarsi come il fondatore della dinamica, principalmente per i suoi studi e per le sue osservazioni sperimentali sul moto dei gravi (Discorsi e dimostrazioni matematiche, intorno a due nuove scienze attenenti alla mecanica e i movimenti locali, 1638). Importanti furono anche i contributi di Cartesio, con una delle prime formulazioni della legge d’inerzia nei Principia Philosophiae (1644), e di C. Huygens che, determinando la forza centrifuga in un moto rotatorio (Horologiorum oscillatorium sive de motu pendululorum ad horologia aptato demonstrationes geometricae, 1673), studiò, in un caso particolare, l’influenza del sistema di riferimento sull’aspetto del moto. A partire dal 18° sec. la dinamica si è sviluppata suddividendosi in varie branche, principalmente in relazione alla schematizzazione adottata per rappresentare i corpi: sono sorte la dinamica dei solidi, la dinamica dei sistemi continui e deformabili, la teoria matematica dell’elasticità, la fluidodinamica. Al loro sviluppo hanno contribuito, fra gli altri, J.-B. D’Alembert, L. Euler, G.L. Lagrange, L. Poinsot, A.-L. Cauchy, G. Bernoulli, K. Gauss. Successivamente con H. Hertz, E. Mach e A. Einstein, si è sviluppata una critica dei principi che è sfociata nella teoria della relatività ristretta (A. Einstein, 1905) prima e poi nella relatività generale (A. Einstein, 1916), alla base delle quali è l’abolizione dei concetti di spazio e tempo assoluti. Parte essenziale delle teorie relativistiche è la dinamica relativistica (➔ relatività). Sebbene questa abbia avuto importanza fondamentale per lo sviluppo della fisica moderna, la dinamica classica, che ne costituisce il limite corretto nella trattazione di tutti i fenomeni ‘lenti’ (rispetto alla luce), nulla ha perduto del suo valore teorico e pratico, poiché le correzioni relativistiche risultano assolutamente trascurabili nella massima parte dei problemi della tecnica.

Principi della dinamica classica

Nei suoi Philosophiae naturalis principia mathematica (1687) Newton precisa in modo universale l’interdipendenza tra forza e movimento attraverso la legge fondamentale della dinamica (o secondo principio della dinamica): la variazione della quantità di moto di un corpo di massa m è proporzionale alla forza complessiva agente su di esso, la quantità di moto essendo misurata dal prodotto della velocità per la massa; cioè con le attuali notazioni vettoriali:

Se la massa non varia nel tempo, indicando con a l’accelerazione del corpo, si ha la relazione nota come ‘equazione fondamentale della meccanica’

[1] formula

ovvero l’accelerazione di un corpo è pari al rapporto tra la forza complessiva agente su di esso e la sua massa. Il corpo si intende assimilato a un punto materiale, cioè un modello di corpo privo di dimensioni spaziali, ma dotato di massa. La [1] è strettamente valida in un sistema di riferimento inerziale, ovvero un riferimento nel quale vale la legge di inerzia (o primo principio della dinamica): ogni corpo persevera nel suo stato di quiete o di moto rettilineo uniforme fintanto che non interviene una causa esterna (forza) a determinarne una variazione. Noto un sistema di riferimento inerziale, lo sono tutti quelli in moto traslatorio rettilineo uniforme rispetto al primo (relatività galileiana). Un sistema di riferimento con origine nel Sole e assi orientati in maniera invariabile rispetto alle stelle fisse è, solo approssimativamente, inerziale; anche un riferimento solidale con la Terra è non inerziale. Il quadro delle leggi della dinamica si completa con il principio di azione e reazione (terzo principio della dinamica): se su un corpo A agisce una forza F da parte di un corpo B, su B agisce una forza eguale e contraria agente lungo la medesima retta di applicazione. Ammessa infatti valida la [1] per un riferimento inerziale, se si vuole passare a un riferimento mobile con moto non traslatorio rettilineo uniforme rispetto al primo, cioè se si vuole attribuire ad a il significato di accelerazione relativa, alla [1], come si ricava applicando il teorema di Coriolis, va sostituita la

[2] formula

dove a_τ è l’accelerazione di trascinamento e

è l’accelerazione complementare (➔ moto). I due termini −m a_τ e −2 m w_τ × v_r prendono rispettivamente il nome di forza di trascinamento e di forza complementare (o di Coriolis) e, insieme, quello di forze apparenti del moto relativo. Esse non soddisfano il terzo principio della dinamica che, invece, resta valido per le forze che compaiono nei sistemi inerziali cui, per contrapposizione, si dà il nome di forze reali. Naturalmente nulla vieta di scrivere la [2] nella stessa forma, F=m a, della [1], ma la F non è più la stessa che si ha quando si considera il moto rispetto a un riferimento inerziale; la forza effettiva F va corretta con l’aggiunta delle forze apparenti.

La [1] è l’equazione alla quale si deve far capo per determinare analiticamente il moto di un corpo puntiforme libero. Per utilizzarla va opportunamente specificata la legge della forza, cioè, in generale, la sua dipendenza dalla posizione e dalla velocità del punto cui è applicata e, eventualmente, dal tempo. Una volta fatto questo, il problema meccanico è tradotto in un problema analitico. L’equazione vettoriale F=m a, proiettata sugli assi della terna di riferimento Oxyz, dà luogo a un sistema di tre equazioni differenziali del secondo ordine delle tre funzioni incognite x(t), y(t), z(t), coordinate del punto mobile:

[3] formula

ove ẋ=dx/dt, ẍ=d²x/dt² ecc. rappresentano rispettivamente le componenti cartesiane della velocità e dell’accelerazione. Le [3] si riducono a due se il moto è piano; a una se il moto è rettilineo. Integrando tale sistema, operazione che può non esser facile, si vengono a determinare le cosiddette equazioni del moto, x=x(t), y=y(t), z=z(t), cioè le equazioni parametriche della traiettoria (parametro il tempo t). A integrazione effettuata, in esse restano arbitrarie sei costanti (dette costanti di integrazione) che vanno determinate in base alle sei condizioni iniziali, cioè in base ai dati relativi alla posizione e alla velocità del punto mobile all’istante iniziale, generalmente individuate dai corrispondenti elementi cartesiani. Le condizioni iniziali determinano il moto insieme alle forze e devono quindi essere assegnate perché restino univocamente individuate le equazioni del moto.

Se il corpo non può essere assimilato, nel problema che si studia, a un punto materiale, il posto della [1] viene preso dalle cosiddette equazioni cardinali della dinamica dei sistemi. Si tratta di due equazioni vettoriali (quindi di sei equazioni scalari) che legano il risultante e momento risultante delle forze esterne attive e vincolari, agli elementi cinematici del moto. La forma più espressiva che si può dare a tali equazioni è quella che traduce rispettivamente il teorema della quantità di moto o dell’impulso e il teorema del momento della quantità di moto. Precisamente, indicando con R^(e) e con M^(e), rispettivamente, il risultante e il momento risultante delle forze esterne (calcolato rispetto a un punto O eventualmente in moto con velocità v_O), si ha:

essendo a_C e p l’accelerazione del centro di massa del sistema e la quantità di moto del sistema, rispettivamente, e b il momento risultante delle quantità di moto (anch’esso calcolato rispetto a O). Le equazioni cardinali hanno un posto fondamentale in tutta la dinamica dei sistemi. I motivi della loro importanza sono sostanzialmente due: il primo è che in esse non intervengono le forze interne (che, come insieme di forze a due a due uguali e contrarie, hanno, per il principio di azione e reazione, risultante e momento risultante nullo); il secondo è che le forze esterne intervengono solo per il tramite del risultante e del momento risultante e possono quindi essere sostituite con sistemi equivalenti. Una settima equazione fondamentale è in generale costituita dal teorema dell’energia cinetica o delle forze vive: per ogni sistema materiale in un qualsiasi intervallo di tempo infinitesimo dt, la variazione dT che subisce l’energia cinetica, o forza viva (con formula)

è uguale al lavoro elementare di tutte le forze esterne (dL^(e)) e interne (dL⁽ⁱ⁾) agenti sul sistema nello stesso intervallo di tempo:

Se il sistema è rigido, il lavoro delle forze interne si annulla, l’equazione precedente si riduce a dT=dL^(e), e non è più un’equazione indipendente dal sistema cardinale ma una conseguenza, tuttavia assai utile, di esso. Il teorema delle forze vive si presenta per il punto materiale, per il quale tutte le forze sono esterne, nella stessa forma che per il corpo rigido, e anche per il punto esso è una semplice conseguenza dell’equazione fondamentale. Al lavoro elementare portano in genere contributo sia le forze attive sia le forze vincolari: se si verifica che il lavoro elementare di queste ultime si annulla (e per ciò basta, ma non occorre, che i vincoli siano privi di attrito e indipendenti dal tempo) il teorema delle forze vive si semplifica, per un generico sistema, in

,

e per il punto e per i sistemi rigidi in dT=dL^(e,a). Se, di più, si dà la circostanza che le forze attive siano conservative, la precedente equazione (differenziale del 2° ordine) dà luogo a un integrale primo, detto integrale dell’energia. Indicando con Π l’energia potenziale, uguale al potenziale cambiato di segno, di tutte le forze attive, tale integrale si può porre nella forma

si tratta della particolarizzazione nell’ambito meccanico del generale principio fisico della conservazione dell’energia: durante il moto di un sistema soggetto a forze conservative, ed eventualmente anche a forze vincolari che però non compiano lavoro, l’energia meccanica può trasformarsi da cinetica in potenziale e viceversa, ma la somma delle due resta durante il moto inalterata e uguale al valore E che essa ha all’istante iniziale. La costante E ha il nome di costante dell’energia ed è appunto determinabile in base alle condizioni iniziali.

Matematica

Dinamica discreta

Trasformazione di coordinate che, applicata a un dato iniziale e iterata n volte, approssima la soluzione di un’equazione differenziale valutata al tempo αn, con lo stesso dato iniziale; il parametro α è detto ‘passo di integrazione’; si richiede che nel limite α → 0 gli errori di approssimazione si annullino. Per es., l’equazione (dx/dt)=f(x), x(0)=x₀, può essere discretizzata dalla trasformazione x′=x+αf(x). Ponendo xn₊₁=xn + αf(x), x(0)=x₀ si ha che xn approssima x(αn) e tende a questo per α → 0, n → ∞ e t=αn fissato. La discretizzazione interviene quando si vuole affrontare lo studio numerico di un’equazione differenziale, e la scelta del passo di integrazione opportuno è molto importante.

Dinamica simbolica

Se S è una trasformazione di un insieme F (spazio delle fasi) in sé stesso e F viene suddiviso in s sottoinsiemi disgiunti I₁, …, Is, si può associare a ogni traiettoria Skx (k=1, 2, …) una successione i₁ , i₂ , … dove, per ogni k, ik è l’indice tale che Skx∈Iik. In questo modo a ogni punto dello spazio delle fasi è associata una successione di simboli i₁, i₂ , … detta storia H(x) di x sulla partizione I₁, …, Is. L’azione di S sui punti di F può essere vista semplicemente come la traslazione delle intere successioni che ne rappresentano le storie; la storia del punto Sx si ottiene da quella di x traslando quest’ultima di una unità verso sinistra e cancellando il primo simbolo. Dunque, nel caso in cui le storie determinino univocamente i punti che le generano (e in questo caso la partizione I₁, …, Is si dice separante), la conoscenza della corrispondenza x → H(x), che è detta dinamica simbolica, determina completamente l’azione di S. La dinamica simbolica è interessante nelle applicazioni quando la partizione che la genera può essere scelta in modo che le successioni relative a qualche x siano descrivibili in modo semplice; essa è anche un linguaggio molto naturale e utilizzato per lo studio dell’ergodicità dei sistemi dinamici.

Musica

Per la dinamica in musica ➔ dinamica musicale.