moto

L’atto e l’effetto del muoversi, cioè dello spostarsi di un corpo da una posizione o configurazione a un’altra; si contrappone a quiete ed è sinonimo di movimento, a cui in genere è preferito nel linguaggio tecnico e scientifico, dove assume accezioni proprie e specifiche.

Astronomia

Si chiama m. ognuno degli spostamenti effettivi o apparenti degli astri.

Il m. apparente della sfera celeste (o del Sole, o di un astro) è il m. descritto dalla volta celeste (o, su questa, dal Sole o dall’astro) in conseguenza della rotazione terrestre (m. apparente diurno) e della rivoluzione della Terra intorno al Sole (m. apparente annuo).

Il m. proprio di una stella è lo spostamento angolare della stella lungo un arco di cerchio massimo della sfera celeste, risultante di movimenti effettivi (m. peculiari) o apparenti (m. parallattici) della stella stessa.

M. orbitale Il movimento che un corpo celeste (per es. un pianeta, un satellite o, in generale, il componente di massa minore di un sistema binario) compie nel suo giro di rivoluzione intorno al proprio centro di m. (Sole, pianeta, stella principale del sistema binario) quando, soltanto, si tenga conto della forza di attrazione su di esso esplicata dal corpo posto nel centro del m. (problema dei due corpi). È retto dalle leggi di Keplero: a) le orbite descritte dai pianeti sono ellissi di cui il Sole occupa uno dei fuochi; b) le aree descritte dal raggio vettore sono proporzionali ai tempi impiegati a descriverle; c) i quadrati dei tempi impiegati dai vari pianeti a percorrere le rispettive orbite (periodi di rivoluzione) sono proporzionali ai cubi dei semiassi maggiori delle orbite. Il m. di ciascun pianeta è centrale, col centro nel Sole; l’accelerazione è sempre orientata verso il Sole e ha grandezza inversamente proporzionale al quadrato della distanza del pianeta dal Sole, il fattore di proporzionalità essendo lo stesso per tutti i pianeti.

Filosofia

Dal punto di vista filosofico, il m. è studiato nella più generale prospettiva dei problemi relativi alle varie forme di mutamento e del divenire. M. è per Aristotele non solo il movimento spaziale, ma ogni forma di divenire: e perciò egli può considerare il m. come l’aspetto comune di ogni passaggio di potenza in atto, cioè come realizzazione di ciò che è in potenza. In senso specifico il m. è essenzialmente traslazione e si svolge secondo la linea retta o circolare (m. quest’ultimo proprio dei corpi celesti incorruttibili ed eterni); il m. locale o di traslazione ha per Aristotele la priorità sulle altre forme di mutamento. Nella fisica democriteo-epicurea, poi in quella di origine galileiana e cartesiana, il m. si definisce non come passaggio da potenza ad atto ma come rapporto reciproco di particelle prime, quantitativamente determinate. Quando invece il concetto di m. accentra su di sé lo stesso più generale problema della concepibilità del divenire (Hegel, Bergson) allora si presenta, come al pensiero classico, quale forma tipica o universale del divenire.

In relazione a quello di m., il concetto di motore si presenta nella concezione aristotelica della divinità, intesa come primo motore, cioè come causa suprema di tutto il divenire cosmico, e come motore immobile (κινοῦν ἀκίνητον), cioè come pura attualità affatto scevra di potenza, tale da muovere senza muoversi, come il fine supremo di perfezione a cui tutta la realtà tende. Tale concezione passò poi nella teologia Scolastica.

Fisica

Lo studio, cinematico o dinamico, di un m. richiede che il corpo materiale sia opportunamente schematizzato (in un punto materiale, in un corpo rigido ecc.) in relazione alla natura del problema che si ha di fronte e degli scopi che si perseguono. Occorre poi precisare il sistema di riferimento cui il m. viene riferito, poiché il concetto di m. è per sua natura relativo (di un corpo che sia in quiete rispetto alla Terra si può, per es., dire che è in m. rispetto al Sole ecc.). Il riferimento viene di solito rappresentato, in forma schematica e particolarmente atta agli sviluppi matematici, mediante una terna cartesiana di assi mutuamente ortogonali. Se talvolta non si parla esplicitamente del riferimento, esso è tuttavia sempre sottinteso: in molti problemi della tecnica ordinaria esso è senz’altro la Terra.

Grandezze fondamentali che caratterizzano cinematicamente un m. sono la velocità e l’accelerazione; dal punto di vista dinamico la descrizione o la determinazione del m. sono subordinate alla conoscenza delle forze agenti sul corpo. La conoscenza completa del m. di un corpo richiede la conoscenza sia della traiettoria che il corpo descrive muovendosi sia della legge con cui esso la descrive.

M. di un punto

Ai fini della conoscenza completa del m. è necessaria la conoscenza delle 3 equazioni, dette equazioni del m., che danno le coordinate cartesiane del punto in funzione del tempo; o, ciò che è lo stesso, la conoscenza della traiettoria descritta dal punto in m. e della legge (legge oraria) con cui questa è percorsa. Se sulla traiettoria si pensa fissato un sistema di ascisse curvilinee s, il m. del punto si dice progressivo (o diretto) oppure retrogrado a seconda che esso si svolga nel verso in cui la s, come funzione di t, è rispettivamente crescente o decrescente. Dal punto di vista dell’andamento delle velocità una prima distinzione è da farsi tra m. uniforme e m. vario.

Si dice m. uniforme se da istante a istante la velocità, che è una grandezza vettoriale, rimane costante in modulo potendo però variare in generale di direzione. Quando resta costante anche la direzione della velocità, il m. oltre che uniforme è anche necessariamente rettilineo. In un m. uniforme e rettilineo l’accelerazione è nulla; in un m. uniforme non rettilineo essa non è nulla (➔ accelerazione), ma è nullo il solo componente tangente alla traiettoria in ogni punto. Il cammino percorso in un m. uniforme è funzione lineare del tempo: precisamente esso si ottiene moltiplicando la velocità per il tempo; il diagramma orario, cioè il diagramma del cammino percorso in funzione del tempo, di un m. uniforme è una retta.

Si dice m. vario un m. non uniforme, un m. cioè ad accelerazione tangenziale non nulla; un m. vario si dice, a un dato istante, accelerato o ritardato a seconda che a partire da quell’istante al crescere del tempo t la grandezza della velocità vada crescendo o decrescendo. A seconda che un m. sia a un dato istante accelerato o ritardato, l’angolo formato dal vettore velocità v col vettore accelerazione a è acuto oppure ottuso. Un particolare m. vario è il m. uniformemente vario: si tratta di un m., su una traiettoria qualsiasi, in cui l’accelerazione tangenziale è costante in modulo mentre quella normale può variare da istante a istante (di modo che l’accelerazione vettoriale non è in generale costante). Un particolare esempio è dato dal m. nel vuoto di un grave lungo la verticale, uniformemente ritardato se il corpo sale verso l’alto, accelerato se scende lungo la verticale: in ambedue i casi l’accelerazione tangenziale, cui si riduce tutta l’accelerazione, è quella di gravità, concorde con la velocità se il m. è discendente, discorde se è ascendente. In un m. uniformemente vario la velocità scalare e lo spazio percorso sono rispettivamente funzione lineare e quadratica del tempo; il diagramma orario è parabolico con l’asse di simmetria parallelo all’asse delle s.

Il m. di un punto si dice poi piano, spesso in contrapposizione a spaziale, quando la traiettoria appartiene interamente a un piano. In un m. piano si riducono da 3 a 2 le equazioni cartesiane del m., nonché le componenti della velocità e dell’accelerazione. Questi 2 ultimi vettori, oltre a essere suscettibili delle espressioni cartesiane, possono essere soggetti per comodità a una decomposizione secondo le direzioni del raggio vettore (direzione radiale) e della sua normale (direzione trasversa), che fa capo alle coordinate polari.

Sono di seguito descritti alcuni m. particolari di un punto.

(fig. 1

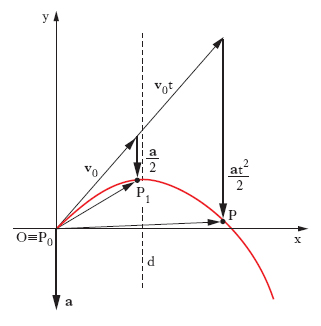
M. ad accelerazione costante o uniformemente accelerato M. in cui l’accelerazione a si mantiene costante da istante a istante, vettorialmente. In un generico m. ad accelerazione costante la velocità vettoriale è funzione lineare del tempo, cioè v = at + v₀, ove v₀ è la velocità iniziale; il vettore OP che va dall’origine O degli assi alla posizione occupata dal punto mobile all’istante generico t, è funzione di 2° grado di t: precisamente, scegliendo O coincidente con la posizione iniziale P₀ (fig. 1) di P, si ha OP = v₀t + at²/2. La traiettoria è una parabola uscente da O, tangente in O a v₀, con asse d parallelo alla direzione dell’accelerazione, che degenera in una retta se la velocità iniziale è nulla o diretta come a. In questo caso l’accelerazione viene a essere tutta tangenziale e il moto è uniformemente vario.

fig. 2

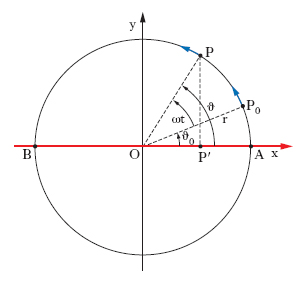
M. circolare M. di un punto P su una circonferenza. Se P₀ (fig. 2) è la posizione iniziale di P e ϑ₀ (fase iniziale) è l’anomalia di P₀ nell’istante t₀ dal quale si comincia a contare il trascorrere del tempo, in un sistema di riferimento il cui polo è nel centro O della circonferenza e il cui asse polare è una certa retta OA, l’anomalia (o fase istantanea) per la generica posizione P del punto vale ϑ = ϑ₀ + ʃ^t_t0 ω(t)dt, essendo ω la velocità angolare, cioè la derivata dell’anomalia rispetto al tempo. Se ω è costante si ha: ϑ = ωt + ϑ₀, il m. si dice circolare uniforme e la fase è una funzione lineare del tempo. La velocità v, diretta secondo la tangente alla circonferenza, vale in modulo rω, essendo r il raggio della circonferenza; l’accelerazione a, nel caso di m. uniforme, è puramente centripeta (o, e in questo caso è lo stesso, radiale) e la sua grandezza vale ω²r. Il m. è periodico, di periodo T = 2π/ω; in funzione della frequenza ν (inverso del periodo), velocità e accelerazione restano rispettivamente espresse da υ = 2πνr, a=4 π²ν²r. In un m. circolare non uniforme la velocità è ancora, istante per istante, esprimibile mediante il prodotto ωr, ma ω=ϑ. non è più costante; si ha un’accelerazione angolare ϑ¨ e l’accelerazione di P non è più totalmente centripeta: essa ha anche una componente

tangenziale e la sua grandezza è r√‾‾‾‾‾‾ϑ. ⁴+ϑ¨ ².‾‾‾.

M. armonico Dato un punto P che si muove di m. circolare uniforme, è il m., rettilineo e periodico, della proiezione P′ di P su un diametro x della circonferenza traiettoria (fig. 2). Se r è il raggio della circonferenza, O il suo centro, x e y la coppia di assi cartesiani di riferimento, ω la velocità angolare costante di P, ϑ₀ la fase iniziale del m. circolare di P, l’ascissa (o elongazione) x di P′, la velocità ẋ e la sua accelerazione ẍ sono, rispettivamente, x=r cos(ωt+ϑ₀); ẋ= − ω r sen(ωt + ϑ₀); ẍ =− ω²x. A differenza del m. di P, il m. di P′ non è uniforme: la velocità di P′ oscilla tra un valore massimo, uguale a ωr, che si ha quando P′ transita per O, centro del m., e un valore minimo nullo, che si ha agli estremi A e B del diametro. L’accelerazione è invece massima in corrispondenza a tali estremi, ove la sua grandezza assume il valore ω²r, ed è nulla in O. La massima elongazione r di P′ da O si chiama ampiezza del m.; ϑ=ωt+ϑ₀ è la fase all’istante t o fase istantanea (ϑ₀ è la fase iniziale); ω/2π è la frequenza; ω la pulsazione o costante di frequenza, che dà la variazione della fase nell’unità di tempo. La x è una variabile armonica; ẋ è un’altra variabile armonica, in quadratura (differenza di fase pari a π/2) con la x; l’accelerazione è una terza variabile armonica, in opposizione di fase con l’elongazione (differenza di fase pari a π). La relazione ẍ = −ω²x che passa tra la ẍ e la x è l’equazione caratteristica dei m. armonici: tutte le volte che una funzione x di una qualsiasi variabile è legata alla sua derivata seconda da una relazione di questo tipo si dice che essa soddisfa all’equazione dei m. armonici. Il diagramma orario di un m. armonico è una sinusoide.

M. centrale M. di un punto P per il quale si verifichi la circostanza che la retta del vettore accelerazione in corrispondenza a ogni posizione di P sulla traiettoria passi sempre per un punto fisso C, cui si dà il nome di centro del moto. Un m. centrale è sempre un m. piano, per il quale è costante la velocità areale, cioè la derivata rispetto al tempo dell’area spazzata dal raggio vettore CP. Sono centrali, per es., un m. circolare uniforme (ma non un m. circolare generico), i m. kepleriani, un m. determinato da una forza elastica e più generalmente qualunque m. mantenuto da una forza centrale. M. composto Il m. di un punto P si dice composto di n m. componenti se a ogni istante il vettore OP, che individua in funzione del tempo la posizione di P rispetto a un’assegnata terna di riferimento, può essere dato come risultante degli n vettori, OP₁, OP₂, …, OP_n, che individuano le simultanee posizioni di altrettanti punti in m. Un m. composto generalmente non è piano. Il m. spaziale di un punto si può sempre considerare composto dei m. delle 3 proiezioni del punto sugli assi; il m. parabolico dei gravi nel vuoto (fig. 1) si può considerare composto di un m. rettilineo uniforme sulla linea di proiezione e di un m. uniformemente vario sulla verticale passante per la posizione iniziale. Nel m. composto velocità e accelerazione sono i risultanti rispettivamente delle velocità e delle accelerazioni dei m. componenti.

M. elicoidale Il m. di un punto la cui traiettoria è un’elica.

M. inverso Il m. che si otterrebbe dal m. di un punto invertendo il tempo, ossia l’ordine di successione temporale.

M. libero e m. vincolato Si parla di m. libero di un punto materiale (o anche di un sistema), in contrapposizione a m. vincolato, tutte le volte che il punto (o il sistema) non è soggetto nel suo movimento ad alcun vincolo.

M. oscillatorio M. periodico su traiettoria rettilinea o no; se le posizioni estreme tra le quali si svolge il m. sono fisse, si parla di m. oscillatorio permanente (un m. oscillatorio permanente rettilineo è il m. armonico), mentre si parla di m. oscillatorio smorzato se dette posizioni si vanno progressivamente avvicinando, cioè se l’ampiezza del m. va riducendosi col passare del tempo.

M. periodico M. di un punto in cui a intervalli di tempo multipli interi di un certo intervallo (periodo del m.) il punto riprende la stessa posizione con le stesse caratteristiche cinematiche (velocità, accelerazione ecc.).

M. rigido

fig. 3

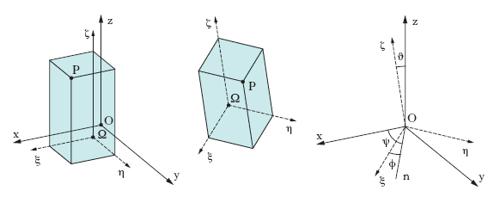
M. di un sistema rigido o che, comunque, si comporti come tale. Lo studio dei m. rigidi si può effettuare pensando associata rigidamente al sistema una terna cartesiana trirettangola (levogira) Ωξηζ, detta terna solidale. Le coordinate dei singoli punti del sistema S rispetto alla Ωξηζ, per la condizione di rigidità, restano durante il m. invariate, pertanto la posizione che occupa nello spazio a un dato istante il generico punto P di S resterà determinata, note che siano le sue coordinate solidali, appena siano noti la posizione di Ω (che si individua mediante le sue coordinate rispetto alla terna fissa di riferimento Oxyz) e l’orientamento della Ωξηζ, rispetto alla Oxyz, individuabile mediante i tre angoli ψ, ϑ, ϕ (fig. 3) detti angoli di Eulero. Questi hanno rispettivamente i nomi di angolo di precessione, di nutazione, di rotazione propria. La retta n, intersezione del piano Oxy con il piano Οξη, retta che forma l’angolo ψ di precessione con l’asse x, si chiama linea dei nodi. Un m. rigido di un corpo determina quindi un m. per tutti i punti dello spazio, quando si pensino rigidamente collegati al corpo o, ciò che è lo stesso, a una terna a esso solidale. Il fondamentale teorema di Mozzi stabilisce che nel più generale m. rigido la distribuzione istantanea delle velocità (atto di m.) è la medesima che si avrebbe in un moto elicoidale; che cioè il m. risulta dalla composizione, istante per istante, di una rotazione intorno a un certo asse (asse di m. o di Mozzi) e di una traslazione nella direzione dell’asse medesimo. Naturalmente ciò non significa che risulti elicoidale il m.: perché ciò si verifichi occorre che l’asse di m. sia invariabile, ciò che in generale non è. Se si indicano con A un punto qualunque dell’asse di Mozzi, con τ e ω la velocità di traslazione e la velocità angolare, comuni a ogni istante a tutti i punti del corpo, ma generalmente variabili da istante a istante sia in grandezza sia in orientamento (con la condizione però di risultare sempre paralleli tra loro e all’asse), il teorema di Mozzi si esprime nella formula

[1] v = τ + ω × AP,

che dà, in funzione degli elementi indicati, la velocità vettoriale v del generico punto P. Se τ si annulla l’atto di m. da elicoidale si riduce a rotatorio (v = ω × AP) e si ha addirittura un m. rotatorio se l’asse di rotazione è fisso. Se si annulla ω il m. si riduce a traslatorio (v = τ). Risulta inoltre dalla [1] che se P appartiene all’asse di Mozzi, v si riduce in ogni caso a τ: i punti dell’asse di Mozzi hanno velocità minima e uguale a τ (in particolare sono fermi se l’atto di m. è rotatorio). Applicando la [1] a un punto Ω che non appartenga all’asse di Mozzi e sottraendo dalla [1] la relazione che così si ottiene, si ha la formula fondamentale della cinematica rigida:

[2] v = v_Ω + ω × ΩP,

che presenta l’atto di m. rigido sempre sotto un aspetto rototraslatorio ma non più elicoidale (v_Ω e ω in generale non sono, come già τ e ω, paralleli fra loro). I due vettori v_Ω e ω sono i due vettori caratteristici del moto rigido (rispetto al polo o centro di riduzione Ω).

Se la terna Oxyz è a sua volta in moto rispetto a un altro riferimento, si parla di m. rigido relativo: allora, oltre alla validità per ciascun punto del corpo del principio dei m. relativi e del teorema di Coriolis, si ha la circostanza che la velocità angolare assoluta coincide col risultante delle due velocità angolari, relativa e di trascinamento: ω_a = ω_r + ω_τ.

Di seguito sono date alcune notizie riguardo a m. rigidi particolari.

fig. 4

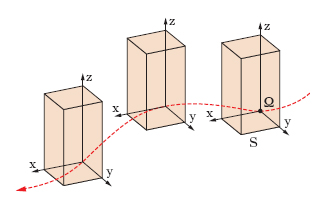
M. traslatorio M. rigido durante il quale ogni retta solidale al sistema S conserva direzione invariabile (fig. 4): il corpo si muove restando, per così dire, parallelo a sé stesso. In un m. traslatorio la velocità angolare è sempre nulla. Le traiettorie dei singoli punti risultano in ogni caso uguali tra loro, sovrapponibili l’una all’altra con una semplice traslazione e percorse con la medesima legge: sicché tutti i punti hanno a un determinato istante la medesima velocità e la medesima accelerazione (variabili però in generale da istante a istante). In definitiva il m. del sistema resta individuato dal m. di un solo suo punto Ω, per cui il numero dei gradi di libertà del sistema si riduce da 6, quale è in un generico m. rigido, a 3. Il vettore che rappresenta la comune velocità dei punti del corpo si chiama velocità di traslazione.

fig. 5

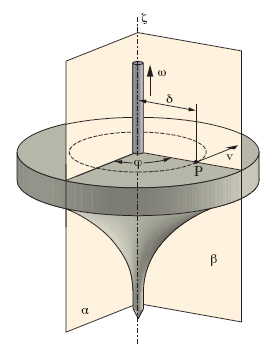
M. rotatorio M. rigido in cui una retta ζ (fig. 5) solidale al sistema rimane fissa. La retta fissa ha il nome di asse di rotazione: a essa è sempre parallelo il vettore velocità angolare ω, la cui grandezza è viceversa, in generale, variabile da istante a istante. Il sistema ha un solo grado di libertà (basta un parametro, per es. l’angolo ϕ formato da un semipiano β solidale al sistema e uscente da ζ con un semipiano fisso α, per individuare la rotazione). Il generico punto P del corpo posto a distanza δ dall’asse si muove, con velocità v = ωδ, sulla circonferenza del piano condotto per P normalmente all’asse, avente il centro sull’asse e raggio δ: il m. di ogni punto è dunque circolare. Se ω oltre che in direzione è costante anche in grandezza e verso, i m. circolari dei singoli punti riescono tutti uniformi, e il m. si dice in tal caso m. rotatorio uniforme. M. rototraslatorio M. rigido in cui una retta solidale al sistema (e quindi, per la condizione di rigidità, ogni retta solidale a essa parallela) conserva durante il m. direzione invariabile. La velocità angolare ha sempre la direzione di questa retta; il sistema ha 4 gradi di libertà (3 parametri per individuare la posizione dell’origine Ω della terna solidale, uno per individuare l’orientamento della terna solidale rispetto alla terna fissa di riferimento). Se la velocità angolare si annulla, il m. si riduce a essere traslatorio. Se la retta resta anche sovrapposta a un asse fisso, il m. si dice m. con asse scorrente su sé stesso o con asse invariabile.

M rigido piano M. rigido in cui ciascuna sezione del sistema parallela a un piano fisso π si mantiene sempre nello stesso piano (cioè tale che a ogni istante la velocità di ogni punto risulti parallela a π): difatti l’andamento di un m. siffatto è, per la rigidità, lungo ogni normale a π, lo stesso che si ha per il piede della normale, pertanto esso può essere descritto semplicemente descrivendo il m. d’un piano mobile p, solidale al sistema, che si mantenga costantemente sovrapposto a π. L’atto di m. in un m. rigido piano non può che essere o traslatorio, con velocità di traslazione parallela a π, o rotatorio, con asse istantaneo di rotazione, a, normale a π. In tale ultimo caso non è però detto che il m. sia rotatorio: ciò richiederebbe che l’asse fosse a ogni istante il medesimo; viceversa generalmente, da istante a istante, esso varia, sia nello spazio solidale al sistema in m., sia in quello fisso. L’intersezione I di a con π e con p si chiama centro istantaneo di rotazione: se il m. è rotatorio, come è invariabile a (asse permanente di rotazione), così è invariabile I; in generale invece la variabilità dell’asse porta di conseguenza che anche il centro varia da istante a istante, e varia sia sul piano mobile sia sul piano fisso. È notevole il fatto che le normali alle traiettorie dei singoli punti del piano mobile si incontrano tutte, istante per istante, nel corrispondente centro istantaneo di rotazione (teorema di Chasles).

M. rigido sferico (o polare). M. rigido in cui un punto O del sistema resta fisso. Il punto O è detto polo della rotazione. La traiettoria del generico punto P del sistema, per la condizione di rigidità, non può che essere una curva della sfera di centro O e raggio uguale alla distanza PO. Il sistema ha 3 gradi di libertà: occorrono, infatti, 3 parametri fra loro indipendenti (per es., i 3 angoli di Eulero) per individuare l’orientamento di una terna solidale Οξηζ rispetto alla terna Oxyz di riferimento. L’asse di m., che anche in questo caso si chiama asse istantaneo di rotazione, passa sempre per O, variando però in generale da istante a istante sia nel corpo (cioè rispetto alla terna solidale Οξηζ) sia nello spazio (cioè rispetto alla terna fissa Oxyz): l’asse di m. dà così origine a due coni, i coni di Poinsot, non necessariamente rotondi, uno costituito da rette del corpo, l’altro da rette dello spazio, che, ove fossero materializzati, rotolerebbero durante il m. l’uno sull’altro senza strisciare, ugualmente a ciò che si verifica per le traiettorie polari in un m. rigido piano (➔ precessione).

M. relativo

Ha il nome di teoria dei m. relativi quella parte della cinematica in cui si studia il m. di un punto o di un sistema di punti rispetto a due riferimenti a loro volta in m. l’uno rispetto all’altro. Sia Oxyz una terna di riferimento convenzionalmente fissa, Ωξηζ una terna in m. rispetto alla prima, P un punto in m. rispetto all’una e all’altra terna. Si dice m. assoluto il m. di P rispetto alla Oxyz; m. relativo il m. di P rispetto alla Ωξηζ; m. di trascinamento il m. rigido dello spazio pensato solidale alla Ωξηζ rispetto alla Oxyz. Corrispondentemente, si dicono velocità e accelerazione assoluta la velocità v_a e l’accelerazione a_a di P rispetto alla Oxyz; velocità e accelerazione relativa la velocità v_r e l’accelerazione a_r di P rispetto alla Ωξηζ; velocità e accelerazione di trascinamento di P la velocità v_τ e l’accelerazione a_τ che avrebbe il punto P all’istante considerato se, anziché essere mobile rispetto alla Ωξηζ, fosse a essa solidalmente unito. Fra le 3 velocità incorre la relazione v_a=v_r+v_τ nota con il nome di principio dei m. relativi. Fra le accelerazioni intercorre invece la relazione, nota come teorema di Coriolis, a_a=a_r+a_τ+a_c, ove a_c=2 ω_τ×v_r è l’accelerazione di Coriolis o complementare (ω_τ è la velocità angolare nel m. di trascinamento). Se il m. di trascinamento è traslatorio rettilineo uniforme, l’accelerazione assoluta si identifica con quella relativa: in tal caso se la terna Oxyz è una terna solidale alle stelle fisse, la terna mobile Ωξηζ si dice inerziale o galileiana.

M. browniano

M. irregolare e continuo di polveri solide (pollini o resine) sospese in un liquido. Osservato già nel 1650 da A. Leeuwenhoek e più tardi da G.-L. Buffon e da L. Spallanzani, venne ascritto per lungo tempo alla presenza di particelle organiche autoanimate in seno al liquido. La sua scoperta viene comunemente attribuita al botanico scozzese R. Brown (1827), che lo studiò per primo, servendosi di un microscopio a forte ingrandimento, come un processo di natura meccanica e non biologica. Interpretato alla luce delle ipotesi più varie (effetti termici, capillari, elettrici o di diffusione nel liquido) venne finalmente, intorno al 1860, ricondotto agli urti molecolari del mezzo sulle particelle sospese. Il fenomeno venne compreso e inquadrato nella teoria cinetica solo dopo il 1905, con la teoria di Einstein del m. browniano, basata sull’idea principale che alle particelle in sospensione in un liquido, benché di dimensioni molto maggiori delle molecole del solvente, si potessero estendere le leggi della meccanica statistica: in particolare, in base al principio di equipartizione dell’energia e alla legge di J.H. van’t Hoff, anche le particelle browniane devono esercitare una pressione osmotica su una membrana in seno al liquido, previsione contraria alla termodinamica classica ma non alla meccanica statistica.

Altre qualificazioni del termine

M. del centro di massa Il centro di massa di un qualsiasi sistema materiale si muove in ogni caso come si muoverebbe un punto materiale che avesse massa uguale alla massa totale del sistema e fosse sottoposto a una forza uguale al risultante delle forze esterne agenti sul sistema medesimo. Direttamente, quindi, nessun fenomeno interno può modificare il m. del centro di massa. Ne consegue che se il sistema è isolato, cioè non soggetto ad alcuna azione esterna, o se è nullo il risultante delle forze esterne, il suo centro di massa deve o essere in quiete o muoversi di m. rettilineo uniforme (conservazione del m. del centro di massa).

M. impulsivo M. di un sistema i cui punti, in conseguenza di urti, subiscano, in un certo intervallo di tempo, generalmente brevissimo, brusche variazioni di velocità senza che simultaneamente il sistema cambi in modo sensibile di posizione.

M. incipiente In generale, andamento iniziale del m. di un corpo: m. incipiente di una ruota, di un giroscopio ecc. In particolare, la legge del m. incipiente stabilisce che l’orientamento iniziale del m. di un punto che prenda a muoversi, a partire dalla quiete, sotto l’azione di una forza, coincide con quello della forza.

M. irrotazionale e m. rotazionale M. irrotazionale è un m. in cui risulta identicamente nullo il rotore del vettore velocità della generica particella. Nel m. di un qualunque sistema deformabile lo spostamento elementare di una particella si può pensare decomposto in 3 addendi, dei quali uno riassume la vera e propria deformazione, mentre gli altri due corrispondono rispettivamente a una traslazione e a una rotazione; la velocità angolare ω di quest’ultima risulta essere legata alla velocità v della particella dalla relazione ω = rot v/2, e proprio di qui ha avuto origine la qualifica di irrotazionale per il m. in esame e anche lo stesso termine rotore. In altri termini un m. irrotazionale è un m. in cui non si ha per così dire un rimescolamento, una rotazione intrinseca delle particelle fluide. Dal punto di vista matematico la proprietà dell’annullarsi identico di rot v è equivalente all’altra che il campo della velocità derivi da un potenziale, proprietà che può quindi essere assunta in luogo della prima a definizione di m. irrotazionale. Se il vettore v non deriva da un potenziale, il suo rotore non è identicamente nullo e il moto si dice rotazionale, o anche vorticoso con riferimento alla qualifica di vortice, che, per le proprietà sopra ricordate, si attribuisce al vettore ω = rot v/2.

M. stazionario M. di un sistema continuo (per es. un fluido) in cui l’atto di m. non dipenda esplicitamente dal tempo; cioè in ogni punto dello spazio l’eventuale particella del sistema che vi si trovi a passare vi passi sempre con la medesima velocità.

M. di regime Locuzione usata, soprattutto con riferimento alle macchine, per indicare la fase di m. regolare della macchina che segue a quella di avviamento o in contrapposizione a un funzionamento irregolare.

M. perpetuo Si parla di m. perpetuo con riferimento a una macchina ideale o, più in generale, a un sistema di corpi mobili, che, una volta avviato con un impulso esterno, si mantenga perpetuamente in m. senza che gli sia fornita energia. L’impossibilità di realizzare il m. perpetuo è sancita dal primo e dal secondo principio della termodinamica. Il primo principio stabilisce infatti la conservazione dell’energia e quindi l’impossibilità di realizzare una macchina che crei energia dal nulla (m. perpetuo di prima specie). Il secondo principio della termodinamica stabilisce altresì l’impossibilità di realizzare una macchina che basi il suo funzionamento sull’energia termica prelevata da una sola sorgente di calore tutta alla stessa temperatura (m. perpetuo di seconda specie).

Lingua

In grammatica, in senso ampio, verbi di m., i verbi che esprimono un movimento (per es. andare, correre ecc.); complementi di m., quelli che esprimono le varie relazioni di movimento, distinti in: complementi di m. a luogo («andare a casa»), di m. da luogo («tornare dall’ufficio»); di m. per luogo o attraverso luogo («entrare per la porta»), cui alcuni grammatici aggiungono anche un complemento di m. in o entro luogo, assimilato sintatticamente a un complemento di stato in luogo, ma dipendente da un verbo di movimento («aggirarsi nel giardino»).

Musica

Modo con cui procede una linea melodica. Può essere ascendente o discendente, si ha m. congiunto se essa procede per intervalli di tono o semitono, m. disgiunto quando procede per intervalli più ampi. Con riferimento all’andamento di due voci si parla di m. retto, se esse procedono parallelamente; m. contrario, se una scende mentre l’altra sale; m. obliquo, se una si muove mentre l’altra rimane ferma su una stessa nota.

M. perpetuo Composizione virtuosistica basata sulla ripetizione ostinata e senza pause di una stessa, rapida, figura ritmica. Il termine fu usato per la prima volta da C.M. von Weber nell’ultimo movimento della Grosse Sonate op. 24 per pianoforte; tra gli altri, è celebre quello per violino e orchestra (op. 11) di N. Paganini.