campo

Biologia

C. morfogenetico Area dell’embrione, o del primordio di un germoglio, dotata della capacità di dare origine a un determinato organo; per es., i c. morfogenetici dell’arto posteriore danno origine ad arti posteriori, quelli branchiali a branchie ecc. La realizzazione delle capacità di cui è dotato un c. morfogenetico può compiersi sia spontaneamente, sia sotto l’azione di uno stimolo (induzione).

Fisica

Grandezza fisica definita in ciascun punto di una regione dello spazio (e anche la regione stessa).

C. vettoriali

Il c. vettoriale è un c. in cui la grandezza fisica definita è un vettore. C. vettoriali sono il c. della velocità nello spazio occupato da un mezzo continuo in moto, i c. di forza ecc. Si dà la qualifica di costante (o stazionario) ai c. il cui vettore è indipendente dal tempo, pur potendo variare da punto a punto, e di uniforme a quelli il cui vettore è indipendente dal posto, pur potendo eventualmente dipendere dal tempo. Un esempio di c. costante, ma non necessariamente uniforme, è dato dal c. delle velocità per un mezzo continuo in moto stazionario (in ogni punto dello spazio occupato dal mezzo, la velocità è a ogni istante la medesima ma varia in generale da punto a punto). Un c. costante, ma anche uniforme, almeno in una ristretta regione dello spazio prossima alla Terra, è il c. della gravità.

fig. 1

Per un qualsiasi c. vettoriale si chiamano linee del c. (fig. 1) o linee di flusso le linee la cui tangente dà in ogni punto la direzione del vettore. Se il c. è costante le linee di flusso sono a ogni istante le medesime, altrimenti esse variano da istante a istante. Se il c. è uniforme le linee di flusso sono a ogni istante rette fra loro parallele. C. di forza C. vettoriale della forza agente sull’unità di massa, di carica elettrica ecc., detta intensità del c. o forza del c., o anche semplicemente campo. Le linee di flusso di un c. di forza si chiamano anche linee di forza; se il c. è conservativo, cioè deriva da un potenziale monodromo, ha un senso semplice e preciso parlare di superfici equipotenziali e le linee di forza risultano in ogni punto a esse normali.

C. centrale

C. di forza in cui: a) la retta d’azione del vettore del c. in un generico punto P è la congiungente di P con un punto fisso C detto centro del c. o della forza; b) il modulo del vettore è funzione soltanto della posizione di P, per es., tramite la distanza r di P da C. In questo caso la forza può essere espressa nella forma F=f(r)u, dove per u si intenda il versore di PC: f(r) sarà positiva o negativa a seconda che il c. sia attrattivo o repulsivo. Un c. centrale di questo tipo deriva dal potenziale U=−ʃf(r) dr, e la U risulta funzione uniforme e regolare in tutto lo spazio eccettuato al più il punto C; le linee di forza sono le rette passanti per C, le superfici equipotenziali sono le sfere di centro C. È di tal genere il c. elettrostatico generato da una carica puntiforme.

C. conservativo

C. vettoriale nel quale le componenti v_x, v_y, v_z del vettore v del c. coincidono con le derivate parziali di una medesima funzione monodroma, U, del posto, detta potenziale: v_x = δU/δ_x, v_y = δU/δ_y, v_z = δU/δ_z; si può cioè scrivere: v = grad U, cioè il vettore del c. è il gradiente del potenziale. Spesso, particolarmente nell’elettromagnetismo, si assume invece v = − grad U. In un c. conservativo la circuitazione elementare del vettore (cioè, se si tratta di una forza, il lavoro elementare della forza) coincide con il differenziale totale della U; la circuitazione estesa a un arco s collegante due punti A e B non dipende mai dalla forma dell’arco e risulta eguale alla differenza fra i valori che U assume nel punto di arrivo e nel punto di partenza. In particolare la circuitazione estesa a una qualsiasi linea chiusa si annulla; ciò significa, se il c. è un c. di forza, che il lavoro delle forze del c. lungo la linea chiusa è nullo o, se si vuole, che si torna al punto di partenza conservando la stessa energia con cui si era partiti: di qui la denominazione di conservativo data a un c. siffatto.

C. coulombiano

C. vettoriale, di natura qualsiasi, che segua la legge di Coulomb: cioè di un c. centrale, di centro O, in ogni punto P del quale il vettore del c. ha grandezza inversamente proporzionale al quadrato della distanza di P da O. In tale significato generico, è sinonimo di c. newtoniano.

C. di dipolo

C. di forza generato da un dipolo. Detto m il momento del dipolo, l’intensità del c. vale − grad [k m • r/r₃], dove k è una costante che dipende dalla natura del dipolo, dalla natura del mezzo in cui il c. si svolge e dal sistema di unità di misura adottato, e il vettore r è la distanza orientata dal dipolo al punto considerato.

C. di gauge

C. vettoriale fondamentale nelle teorie di c. che possiedono invarianza locale o di gauge.

C. irrotazionale

C. vettoriale per il quale il rotore del vettore v del campo è identicamente nullo. In un c. irrotazionale, per il teorema di Stokes, si annulla la circuitazione di v relativa a una qualsiasi linea chiusa all’interno. Un c. irrotazionale deriva sempre da un potenziale: se la regione in cui il c. è definito è semplicemente connessa, il potenziale è una funzione monodroma e il c. è conservativo.

C. radiale

C. vettoriale in cui la retta d’azione del vettore del c. in un generico punto P è la congiungente di P con un punto fisso C.

C. rotazionale

C. vettoriale per il quale il rotore del vettore del c. non è identicamente nullo (➔ vortice).

C. ruotante

C. vettoriale il cui vettore in un punto generico vari da istante a istante come varierebbe un vettore che ruotasse intorno al punto.

C. solenoidale

C. vettoriale in ogni punto del quale sia nulla la divergenza del vettore del campo: div v = 0. Proprietà caratteristica di un tale c. è l’annullarsi del flusso del vettore attraverso una qualunque superficie chiusa immersa nel campo. Esempi di c. solenoidali sono il c. del rotore di un qualsiasi vettore, quello del vettore induzione magnetica.

C. elettrico

fig. 2

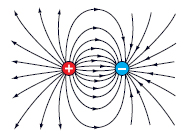
C. elettrico è la denominazione generica indicante un c. di forza agente su cariche elettriche, comunque generato. Il vettore del c. (v. rappresentazione delle linee di forza in fig. 2), indicato generalmente con il simbolo E, ha il nome di intensità del c. elettrico ed è, punto per punto, la forza che agisce sulla carica unitaria positiva posta in quel punto; la forza f agente sulla generica carica q è data quindi dalla relazione f = q E. Unità di misura di E nel Sistema Internazionale (SI) è il volt al metro (V/m). Se a generare il c. sono cariche di valore costante nel tempo e in quiete, localizzate o distribuite che siano, si parla di c. elettrostatico: si tratta di un c. conservativo, derivante da un potenziale V (potenziale elettrico), legato a V dalla relazione E = − grad V. Nel caso che il c. sia generato da una sola carica puntiforme, Q, per l’intensità e il potenziale nel generico punto P a distanza r da Q si ha

E = [Q/(4πεr²)] vers r; V = Q/(4πεr),

dove il vettore r è orientato da Q verso P, ε è la costante dielettrica assoluta del mezzo (omogeneo, isotropo) e per il potenziale si assume il valore zero a distanza infinitamente grande da Q (in pratica: a distanza tanto grande che le azioni elettriche generate da Q siano inapprezzabili). Se il c. è generato da più cariche puntiformi, E è il risultante (vettoriale) dell’intensità dei c. generati dalle singole cariche, V è la somma (algebrica) dei corrispondenti potenziali (principio di additività dei c. elettrici); se è generato da cariche distribuite su linee, su superfici o entro volumi, V viene calcolato mediante relazioni integrali ed E viene poi ottenuto calcolando il gradiente di V cambiato di segno (➔ elettrostatica). L’energia di un c. elettrico (quella che occorre spendere per creare il c. e che si rende nuovamente disponibile ove il c. venga distrutto) ha una densità che vale, punto per punto e istante per istante, εE²/2. Le proprietà dei dielettrici (➔ dielettrico) richiedono l’introduzione del vettore induzione del c. elettrico D=εE (➔ induzione); il c. vettoriale di cui D è il vettore prende il nome di c. di induzione elettrica; si tratta di un c. non solenoidale: precisamente, la divergenza di D è, punto per punto, pari alla densità ρ delle cariche ‘vere’, cioè non di polarizzazione. Anche il c. elettrico è non solenoidale: però per E sono sorgenti, cioè punti in cui la divergenza è diversa da zero, anche le cariche di polarizzazione dielettrica. Ciò significa che in generale per una completa descrizione delle proprietà del c. occorrono, insieme, E e D; soltanto nel vuoto queste due grandezze hanno identiche proprietà vettoriali. C. elettrostatico C. elettrico generato da una distribuzione statica di cariche elettriche costanti.

C. frenante

Genericamente, c. elettrico che fa diminuire la velocità di particelle cariche in moto.

C. elettromotore

C. al quale è dovuto il fluire di una corrente elettrica in un conduttore. A rigore, qualunque c. elettrico, in quanto capace di provocare l’ordinato movimento di cariche elettriche in esso immerse, può considerarsi un c. elettromotore. Tuttavia le cariche costituenti la corrente finirebbero con il neutralizzare quelle inizialmente possedute dai corpi generanti il c., azzerandolo. Perché ciò non accada occorre fornire ai corpi in questione cariche elettriche in misura corrispondente alle cariche su essi convogliate dalla corrente, e con opposto segno. È quanto avviene, per es., nell’interno di una pila chimica chiusa su un conduttore metallico: in virtù di fenomeni di trasformazione di energia potenziale chimica in energia elettrica, ioni trasportano cariche negative dall’elettrodo a potenziale maggiore all’elettrodo a potenziale minore e cariche positive in senso inverso, in tal modo compensando le cariche negative (elettroni di conduzione) che dall’elettrodo a minor potenziale vanno, lungo il conduttore cui la pila è connessa, all’elettrodo a maggior potenziale. A questo campo interno della pila che, contrariamente a quanto fa un c. elettrostatico, fa muovere le cariche positive nel verso dei potenziali crescenti, si attribuisce, in senso specifico, la qualifica di c. elettromotore. C. siffatti si hanno in tutti i cosiddetti generatori di corrente; essi derivano, in generale, dalla trasformazione di energia non elettrica: chimica, termica, luminosa, meccanica. L’intensità del c. elettromotore è la forza agente sulla carica unitaria positiva; il lavoro che le forze del c. elettromotore compiono quando fanno passare l’unità di carica positiva dal morsetto a potenziale minore a quello a potenziale maggiore del generatore, quando questo è in equilibrio, è la forza elettromotrice del generatore.

C. magnetico

fig. 3

Il c. magnetico è un c. di forza agente su magneti, su conduttori percorsi da corrente o su cariche elettriche in movimento, generato da magneti, da conduttori percorsi da corrente o da cariche elettriche in movimento. Il vettore del c. (v. rappresentazione delle linee di forza in fig. 3), indicato generalmente dal simbolo H, ha il nome di intensità del c. magnetico ed è, punto per punto, legato al momento M della coppia di forze che si esercita su un magnete (o più in generale su un oggetto assimilabile a un dipolo magnetico) posto in quel punto dalla relazione M = m×H, dove m è il momento magnetico del magnete (o del dipolo); unità di misura di H è, nel SI, l’ampere al metro (A/m). L’intensità del c. generato da un circuito percorso da corrente vale H = (i/4π) ∮dl× r/r³, dove i è l’intensità della corrente, dl è l’elemento di circuito, orientato nel verso di circolazione della corrente, e l’integrale è esteso all’intero circuito; quella del c. generato da una carica q in moto rettilineo uniforme con velocità v vale H = (q/4π) v × r/r³. La circuitazione di H lungo una linea chiusa L vale ni, dove i è l’intensità della corrente (di conduzione e di spostamento) che genera il c. e n è l’indice di concatenazione tra L e il circuito in cui scorre la corrente: ciò significa che il c. magnetico è conservativo soltanto se è generato da magneti (in tal caso, i=0 e la circuitazione di H lungo una qualunque linea chiusa nel c. è nulla). Introdotto poi il vettore induzione del c. magnetico o induzione magnetica, B, pari al prodotto di μ per H, la forza (azione elettrodinamica) che il c. esercita su un conduttore percorso da corrente vale F=ʃVj×B dV, essendo j la densità di corrente e V il volume occupato dal conduttore; la forza (forza di Lorentz) che il c. esercita su una carica q in moto con velocità v vale poi f = qv×B (➔ elettromagnetismo), unità di misura del cui modulo è, nel SI, il tesla (1T=1Wb/m²). Il vettore B, che dà conto, oltre che delle azioni elettrodinamiche, anche di fenomeni di induzione magnetica ed elettromagnetica (➔ induzione), ha ovunque e sempre divergenza nulla: div B=0. Il c. di induzione magnetica è un c. solenoidale, cioè esso non ammette sorgenti discrete (le sorgenti sono sempre dei dipoli). Per il c. magnetico non si può dire la stessa cosa: infatti, per H sono sorgenti, cioè punti in cui la divergenza è diversa da zero, i punti sulla superficie esterna dei corpi magnetizzati. Nei mezzi materiali, H e B hanno dunque proprietà vettoriali diverse e sono necessari entrambi per descrivere completamente il c.; nel vuoto, invece, non potendo insorgere fenomeni di magnetizzazione, anche H è ovunque solenoidale, e uno solo dei due vettori è sufficiente. La densità dell’energia di un c. magnetico, quella che occorre spendere per creare il c. e che si rende disponibile ove il c. venga rimosso, vale, punto per punto e istante per istante, μH²/2.

fig. 4

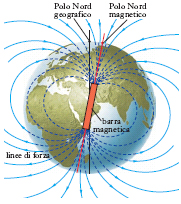
C. magnetico terrestre

C. magnetico esistente intorno alla Terra (fig. 4), assimilabile, con sufficiente approssimazione, a quello generato da un dipolo magnetico posto nel centro della Terra e lievemente inclinato rispetto all’asse della rotazione terrestre (➔ magnetismo).

C. magnetizzante

C. magnetico che provoca la magnetizzazione di un corpo.

C. magnetostatico

C. magnetico generato da magneti di momento costante e in quiete o da conduttori, percorsi da corrente stazionaria, in quiete.

C. elettromagnetico

Il c. elettromagnetico è un c. vettoriale che si propaga nello spazio, costituito da un c. elettrico (componente elettrico) e da un c. magnetico (componente magnetico) le cui intensità, E e H, sono punto per punto e istante per istante ortogonali tra loro e variano nel tempo con la stessa legge: se questa è sinusoidale, anche il c. prende la qualifica di sinusoidale. In generale, un c. elettromagnetico è generato da una corrente elettrica variabile; la corrente genera tutto intorno un campo magnetico variabile e le variazioni di questo generano, a loro volta, un campo elettrico variabile, le cui variazioni generano un c. magnetico variabile e così via: i due campi così generati si propagano nello spazio. Le equazioni rappresentative del c. elettromagnetico sono le equazioni di Maxwell (➔ elettromagnetismo). Al c. elettromagnetico è associata un’energia la cui densità, variabile da punto a punto e istante per istante, vale EH√‾‾εμ, con ε costante dielettrica assoluta e μ permeabilità magnetica assoluta del mezzo in cui ha sede il campo. Si tratta di un’energia che si propaga, come il c. elettromagnetico, tutt’intorno alla sorgente del c. con velocità v=1∣√‾‾εμ; la direzione e il verso della propagazione sono quelli del cosiddetto vettore di Poynting, P, definito dalla relazione P=E×H: il valore medio nel tempo del flusso di tale vettore attraverso una superficie dà l’energia che fluisce nell’unità di tempo attraverso la superficie in questione. Comunque complesse, le funzioni che danno l’andamento nel tempo di E e H, in un determinato punto, possono essere espresse, a norma di un teorema di Fourier, come somme di un certo numero (teoricamente infinito) di funzioni sinusoidali: il che equivale a dire che un c. elettromagnetico può sempre pensarsi come risultante di c. sinusoidali. Riferendoci, per semplicità, a un solo c. sinusoidale, consideriamo le superfici luogo dei punti in cui E e H hanno la stessa fase: si riconosce che l’energia del c. si propaga, nel verso di P e con velocità v, per onde elettromagnetiche le cui superfici d’onda (fronti d’onda) sono quelle anzidette.

C. elettromagnetico di radiazione

È il c. elettromagnetico propriamente detto, caratterizzato dal fatto che i vettori E e H variano in accordo di fase tra loro, talché, risultando il vettore di Poynting mediamente non nullo nel tempo, vi è un’effettiva propagazione di energia raggiante.

C. elettromagnetico d’induzione

Particolare c. elettromagnetico i cui vettori, E e H, variano nel tempo in quadratura di fase tra loro. Come facilmente si verifica, anche il vettore di Poynting risulta in tal caso variabile nel tempo con la stessa frequenza del c., talché l’energia del c. è mediamente nulla: il c. non convoglia energia, ma in esso vi è semplicemente un vicendevole scambio di energia tra il c. elettrico e quello magnetico. Un c. di tal genere si ha, per esempio, in prossimità di un’antenna trasmittente: per tale motivo, in radiotecnica è anche chiamato c. vicino.

Teoria dei campi

Nella teoria dei c., il c. è un sistema fisico a infiniti gradi di libertà il cui stato sia descritto assegnando il valore di una o più grandezze in ciascun punto dello spazio. I processi di interazione si interpretano, sia classicamente sia quantisticamente.

Teoria classica del campo

Questa teoria spiega l’interazione tra due o più corpi mediante la creazione di un c.: l’azione (gravitazionale, elettrica, magnetica ecc.) tra i due corpi non ha luogo direttamente a distanza tra gli stessi, ma ciascun corpo genera nello spazio qualcosa di fisicamente reale, il c., che si manifesta con l’azione sull’altro corpo e che sussiste anche in assenza di questo. In tal modo il c. media l’interazione tra i corpi che è ricondotta a un’azione locale. La teoria classica del c. è formalmente analoga alla meccanica dei mezzi continui.

Teoria quantistica del campo

Il concetto fondamentale di questa teoria è che il c. di interazione generato da una particella sia costituito dalle particelle virtuali emesse e riassorbite in continuazione dalla particella stessa, le quali interagiscono con altre particelle (reali) poste nelle adiacenze della prima particella. Le particelle virtuali che costituiscono il c. sono i cosiddetti quanti del c. e sono tipiche dell’interazione che si considera: una carica q_A posta in un punto dello spazio riempie lo spazio circostante di fotoni virtuali (quanti del c. elettromagnetico, cioè portatori dell’interazione elettromagnetica), i quali vengono continuamente emessi e riassorbiti dalla carica stessa e costituiscono il c. da essa generato; quando si pone una seconda carica q_B in prossimità di q_A fotoni virtuali emessi da q_A urtano q_B (e viceversa) originando l’interazione. Il numero di fotoni virtuali per unità di superficie decresce con la distanza r dalla carica come 1/r² che è proprio la legge con cui decresce il c. elettrostatico. Si parla di emissione di particelle virtuali in quanto le particelle emesse, per non violare il principio di conservazione dell’energia, debbono essere riassorbite prima che sia trascorso l’intervallo di tempo Δt~ħ/E (dove ħ è la costante di Planck divisa per 2π ed E l’energia totale della particella virtuale emessa) in accordo con il principio di indeterminazione. La massima distanza alla quale possono giungere le particelle virtuali emesse, cioè Δr ~ cΔt ~ c ħ̄/E (dove c è la velocità della luce nel vuoto), determina il raggio di azione dell’interazione, cioè la distanza massima alla quale si manifesta l’interazione. Poiché i fotoni hanno massa a riposo nulla, la loro energia totale E può essere piccola quanto si vuole e quindi il raggio di azione della forza elettrostatica è infinito.

C. quantizzati e particelle

Con l’avvento della meccanica quantistica il ruolo dei c. è divenuto preminente nell’interpretazione dei fenomeni fondamentali e quindi di tutta la struttura fisica della materia, poiché il concetto di particella è stato riassorbito nel concetto di campo. Il primo passo della quantizzazione di un c. consiste nell’esprimere la forma hamiltoniana, cioè nell’esprimere l’energia del sistema a infiniti gradi di libertà che costituisce il c. come funzione H (q_n, p_n) di un numero appropriato di variabili indipendenti, q_n, e dei corrispondenti momenti coniugati, p_n. Le variabili dinamiche del sistema, funzioni della qn e pn, divengono nella teoria quantistica operatori su uno spazio vettoriale, detto spazio di Hilbert, i cui elementi corrispondono ai possibili stati del sistema fisico. Il problema generale della dinamica, che nella teoria classica richiede la soluzione delle equazioni del moto, nella teoria quantistica si riconduce all’identificazione dei possibili valori (autovalori) dell’energia, e dei corrispondenti stati (autostati) nello spazio di Hilbert.

Per le teorie di c., che coinvolgono un numero infinito di gradi di libertà, non si conoscono, tranne casi particolari, soluzioni complete. Una classe importante di teorie di c. risolubili include tutti quei casi in cui le equazioni del moto sono lineari nei campi. È questo il caso delle equazioni di Maxwell per il c. elettromagnetico in assenza di cariche e correnti e la versione linearizzata delle equazioni della gravitazione di Einstein, valida per c. gravitazionali deboli. In questi casi la soluzione del problema classico si esprime come sovrapposizione lineare di onde di determinata frequenza e direzione di propagazione. Se si scelgono come variabili indipendenti le ampiezze delle singole onde, il sistema c. risulta equivalente a un insieme di oscillatori non interagenti tra loro, cioè di sistemi la cui trattazione è elementare anche a livello quantistico. Ciascun oscillatore del c. può occupare livelli energetici multipli di hν, dove ν è la frequenza classica dell’onda corrispondente. Si dimostra che un’unità di eccitazione, cioè il quanto hν di energia, può essere interpretato come una particella di energia hν e quantità di moto p=h/λ, dove λ è la lunghezza d’onda. Lo stato generico del c., in cui ciascun oscillatore ha un determinato livello di eccitazione, può essere così interpretato come un insieme di particelle con date energie e quantità di moto. In questa maniera, a ogni teoria di c. classica, governata da equazioni lineari, corrisponde una specie di particelle: i fotoni per il campo elettromagnetico, i gravitoni per il campo gravitazionale. Le eccitazioni elementari della teoria dell’elasticità possono anche essere trattate come particelle, dette fononi, anche se non si tratta naturalmente di particelle elementari, ma di moti collettivi del solido.

La situazione si complica enormemente quando i c. obbediscono a equazioni del moto non lineari. In questo caso la separazione del sistema in sistemi elementari non interagenti (gli oscillatori del c.) non può essere eseguita. Esistono tuttavia metodi approssimati per la soluzione del problema: il metodo perturbativo è quello che ha sinora dato i risultati più rilevanti, specie nell’elettrodinamica quantistica. In questo metodo si approssima la teoria non lineare con una teoria lineare che viene quantizzata come detto sopra, e si trattano le non linearità come perturbazioni delle quali si calcolano gli effetti per approssimazioni successive. Così come una teoria di c. quantizzato può essere descritta in termini di particelle, si può rappresentare una teoria di particelle come teoria di campo. Se si tralasciano le interazioni tra particelle, si otterrà un c. che obbedisce a equazioni del moto lineari e si introdurranno interazioni tra le particelle mediante non linearità nelle equazioni del moto.

C. di gravità

È il c. della forza di gravità, o forza peso, cioè il c. delle forze che la Terra esercita sui corpi materiali; il vettore del c., la forza agente sulla massa unitaria, è l’accelerazione di gravità.

C. gravitazionale

È il c. della gravitazione universale. Il c. gravitazionale generato da una massa puntiforme è un c. di forza centrale, la cui intensità vale, a norma della legge di Newton sulla gravitazione universale, f=G/m r², ove G è la costante di gravitazione universale, m la massa che genera il c., r la distanza fra il centro O del campo, in cui si immagina concentrata la massa m, e il punto che si considera.

C. nucleare

È il c. delle forze nucleari, delle forze cioè che tengono insieme le particelle costituenti il nucleo atomico (➔ forza).

C. mesonico

Secondo la teoria sviluppata nel 1935 da H. Yukawa, particolare tipo di c. nucleare, rappresentante forze a corto raggio derivanti da un potenziale. La denominazione deriva dal fatto che i quanti di tale campo debbono avere massa intermedia tra quella dell’elettrone e quella del protone (mesoni).

C. di radiazione

Regione dello spazio nella quale sono presenti radiazioni corpuscolari o ondulatorie che si propagano in tutte le direzioni con energie diverse.

C. della radiazione universale (o di fondo)

C. di radiazione, con spettro coincidente con quello di un corpo nero a 2,7 K, residuo della radiazione elettromagnetica emessa nelle prime fasi di espansione dell’Universo. Predetta verso il 1948 da G. Gamow, fu scoperta nel 1965 da A. A. Penzias e R. W. Wilson (➔ cosmologia, big-bang).

Informatica

Parte di una istruzione o di una struttura dati, in cui può essere memorizzato uno tra un insieme di possibili dati (ingl. field). Il campo può essere formato sia da un insieme di bit (che, all’interno di una istruzione, ne definiscono una particolarità), sia da un insieme di caratteri (o byte) adiacenti, corrispondenti a una unità di informazione.

Linguistica

C. d’accentazione Insieme delle sedi sillabiche che possono portare l’accento nelle parole d’una lingua ad accento relativamente libero (➔ accento).

C. associativo

Insieme dei rapporti che legano un’unità linguistica alle altre unità del medesimo sistema linguistico.

C. di realizzazione

Insieme delle possibili varianti acustico-articolatorie di un fonema.

C. semantico

Secondo J. Trier, l’insieme dei significati che, nell’ambito di una determinata lingua e tradizione culturale, si presentino affini. Così nell’antico alto tedesco o nel latino tardomedievale i significati di ‘scienza’, ‘tecnica’, ‘ragione’, ‘attività artistica’ si presentano collegati in un campo semantico unitario, unità garantita e attestata dalla possibilità di sostituzione dei vocaboli esprimenti queste nozioni. L’analisi sincronica e diacronica dei c. semantici è al centro di indagini della moderna semantica storica.

Matematica

In algebra, in particolare nello studio delle strutture algebriche, corpo commutativo (➔ corpo). Poiché i corpi numerici che si incontrano nelle matematiche elementari sono tutti commutativi, si parla di c. razionale, c. reale, c. complesso per indicare, rispettivamente, l’insieme dei numeri razionali, dei numeri reali, dei numeri complessi considerati in relazione alle ordinarie operazioni algebriche. Dal punto di vista dell’algebra due c. isomorfi (➔ isomorfismo), nei quali cioè sono astrattamente definite le stesse operazioni, vanno considerati come un unico ente.

Dello studio dei c. di fronte alla relazione di isomorfismo si occupa la cosiddetta teoria dei c. astratti, fondata da E. Steinitz in una sua memoria del 1910.

Nello studio dei c. ha particolare importanza l’operazione di aggiunzione, che fa passare da un c. C a un suo ampliamento o sopracampo. A partire da un dato c. C, gli ampliamenti di C si distribuiscono in due grandi categorie: gli ampliamenti algebrici di C, in cui ogni elemento è algebrico rispetto a C, e gli ampliamenti trascendenti in cui ci sono anche elementi trascendenti. Per i primi si dimostra che, dato un c. C qualunque, esiste uno (e, a meno di isomorfismi, uno solo) ampliamento algebrico massimo (del quale cioè non esistono ulteriori ampliamenti algebrici) che si chiama la chiusura algebrica di C, e si indica di solito con C̅ (C̅ si dice esso stesso c. algebricamente chiuso). Il c. C̅ gode della notevole proprietà che un qualunque ampliamento algebrico di C è contenuto, a meno di isomorfismi, in C̅. Per quanto riguarda i secondi si dimostra che un ampliamento trascendente qualunque di C è un ampliamento algebrico di un ampliamento trascendente puro di C (ottenuto aggiungendo a C un certo numero, finito o infinito, di elementi trascendenti). Con riguardo ai c. più elementarmente noti, se, per es., C è il c. razionale, C̅ è il cosiddetto c. dei numeri algebrici (radici di equazioni a coefficienti razionali). Dire che non tutti i numeri reali sono algebrici, equivale a dire che il c. reale non può essere ottenuto da quello razionale unicamente mediante ampliamenti algebrici. Se C è invece il c. reale, C̅ è il c. complesso. Dire che il c. complesso è algebricamente chiuso, equivale ad affermare il cosiddetto teorema fondamentale dell’algebra (ogni equazione algebrica di grado n, a coefficienti complessi, possiede esattamente n radici). Un particolare interesse teorico offrono i c. finiti. Si dimostra che ogni corpo finito è commutativo, ossia è un c. ed è isomorfo a un c. di Galois (➔ Galois Évariste).

Medicina

C. visivo Lo spazio illuminato che può essere abbracciato dallo sguardo tenendo fisso in un punto un solo occhio (c. visivo monoculare) o entrambi (c. visivo binoculare). Normalmente il c. visivo di ciascun occhio è più esteso lateralmente, un po’ meno in basso, ancora meno in alto e dal lato nasale. Abnormi limitazioni del c. visivo possono manifestarsi per cause morbose, quali le lesioni del nervo ottico, retiniti, tumori cerebrali ecc. L’ampiezza del c. visivo, che può essere grossolanamente delineata spostando un corpo nelle diverse direzioni, si può determinare con esattezza mediante l’uso di un apposito apparecchio (campimetro).

Preistoria

Campi di urne Denominazione di un aspetto culturale, proprio dell’età del Bronzo finale (dal 9° all’11° sec. a.C. circa), che si trova lungo le grandi vie di comunicazione, in Tirolo, Baviera meridionale, Boemia, Austria, Svizzera. È caratterizzato da cimiteri a incinerazione, con urne piriformi o globulari, ricchi corredi funebri di pugnali, coltelli, rasoi, e ornamenti, anche d’oro. L’economia delle popolazioni caratterizzate da questa facies culturale è agricola, con villaggi fortificati; nelle sepolture abbondano le armi. La società dei c. di urne appare caratterizzata da comunità tribali dominate da capi.

Storia

C. di concentramento Luogo di internamento e restrizione della libertà personale per soldati nemici catturati e civili considerati pericolosi per l’ordine interno.

La prima applicazione su vasta scala dell’internamento di civili si ebbe nel corso della guerra anglo-boera (1900-02), quando gli Inglesi trasferirono in c. di concentramento le famiglie dei coloni boeri per domarne la resistenza. I regimi totalitari, tra le due guerre mondiali, li adottarono come strumento di sopraffazione politica e di sterminio in nome di ideologie razziste e di sfruttamento della mano d’opera a sostegno dell’economia. Come mezzo per reprimere il dissenso, vi fecero poi ricorso la Francia in Algeria, gli Stati Uniti in Vietnam, alcuni regimi dell’America Latina; un sistema di campi fu impiantato in Cina durante la Rivoluzione culturale e, in Cambogia, dai khmer rossi. Negli anni 1990, i campi sono ricomparsi in Europa durante le guerre successive alla dissoluzione della Iugoslavia.

C. di concentramento nazisti Sorti in Germania dopo l’avvento al potere di A. Hitler (1933), inizialmente avevano lo scopo di spezzare con il terrore le opposizioni al regime; durante la Seconda guerra mondiale il sistema dei c. di concentramento si diffuse in tutta Europa, seguendo l’avanzata delle armate tedesche verso Est. Da luogo di punizione per prigionieri politici divennero luoghi di sterminio dei «nemici del popolo tedesco», specie ebrei e rom: accanto ai molti c. di lavoro coatto per l’industria di guerra, sorsero veri e propri c. di sterminio dove fu programmata e sistematicamente attuata l’eliminazione dei prigionieri nelle camere a gas. Il numero dei morti nei c. di concentramento nazisti viene calcolato intorno ai 10 milioni, di cui oltre la metà ebrei.

La Repubblica sociale italiana contribuì al tragico bilancio istituendo un c. di concentramento a Fossoli, in provincia di Modena, e organizzando rastrellamenti e deportazioni. Anche la Risiera di San Sabba (Trieste) fu utilizzata come c. di concentramento dai Tedeschi. C. di concentramento sovietici. Istituiti sin dal 1922 per detenere controrivoluzionari e ‘criminali politici’, dopo l’avvento di Stalin, centinaia di c. di lavoro coatto furono impiantati in tutto il paese, specie in Siberia (sistema dei gulag), contribuendo con il lavoro forzato dei detenuti all’industrializzazione del paese. Il processo di destalinizzazione successivo alla morte del dittatore (1953) consentì la riduzione del numero dei c. e la liberazione di centinaia di migliaia di prigionieri.

Sport

Il terreno o, per estensione, l’impianto in cui si svolgono gli incontri sportivi. Deve avere le dimensioni e le caratteristiche specificate dai regolamenti di ciascun gioco. Per gli sport a squadre, riguardo a ciascuna squadra, il c. è detto proprio o avverso, a seconda che l’incontro abbia luogo nella sede propria o in quella dell’avversario. Il campo è detto poi neutro quando, per decisione degli organi federali, o per convenzione, due squadre si incontrano nella sede di una terza.