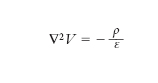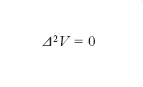elettrostatica

Parte dell’elettrologia che studia i fenomeni cui danno luogo cariche elettriche statiche, cioè con grandezza e posizione determinate e invariabili nel tempo.

Fisica

Le questioni tipiche dell’e. sono lo studio dei campi elettrostatici e quello dei fenomeni che avvengono nella regione sede di un campo elettrostatico: azioni tra cariche elettriche, induzione elettrica nei conduttori, polarizzazione dei dielettrici. Il campo elettrostatico è un campo vettoriale conservativo, il cui vettore, E, è definito operativamente come rapporto tra la forza agente su una carica che non perturbi il campo e il valore della carica stessa, oppure, analiticamente, come il gradiente cambiato di segno del potenziale V, quest’ultimo rappresentando l’energia potenziale dell’unità di carica positiva posta nel campo. L’intensità del campo elettrico è legata alle cariche dalla relazione div(E)=ρ/ε, e alle così dette cariche libere o vere, cioè non di polarizzazione, di densità volumica ρ_L, dalla relazione div(εE)=div(D) = ρ_L, con ε costante dielettrica assoluta (➔ dielettrico) del mezzo in cui il campo si svolge. Il vettore D=εE è il vettore spostamento elettrico, o induzione elettrica (➔ elettromagnetismo). In condizioni elettrostatiche E è nullo nell’interno dei conduttori e lo spazio occupato dai conduttori in questione, anche se sono carichi, è equipotenziale.

Il problema generale dell’e. è il seguente: siano dati vari conduttori, di forma e posizione assegnata, immersi in un mezzo di costante dielettrica assoluta ε, nota che sia la carica q₁, q₂, ..., oppure il potenziale V₁, V₂, ..., del primo, del secondo, ... conduttore, si tratta di determinare l’intensità E del campo in tutto lo spazio (in realtà, basta limitarsi ai vari punti del mezzo, posto che, come abbiamo detto sopra, E è nullo nei punti occupati dai conduttori). In termini analitici, si tratta di risolvere l’equazione:

[1] formula

essendo ∇²V il laplaciano (➔ Laplace, Pierre-Simon de) del potenziale. Tale equazione, nota come equazione di Poisson, risolta sotto la duplice condizione che V decresca proporzionalmente alla distanza r e che ∂V/∂r decresca proporzionalmente al quadrato della distanza, dà:

[2] formula,

l’integrale intendendosi esteso all’intero spazio. È poi E=− grad V. Per determinare V, e quindi E, nei vari punti del mezzo, sempre supposto omogeneo, si può peraltro seguire un’altra via. In tali punti, trovandosi le cariche sulla superficie dei conduttori, è ρ=0 di modo che in luogo della [1] si può considerare la relazione

[3] formula,

che costituisce la classica equazione di Laplace, in cui ci si imbatte in varie questioni di fisica matematica. Se sono noti i potenziali dei vari conduttori, il problema (problema di Dirichlet) si riduce alla determinazione di quella soluzione della [3] che assume i valori V₁, V₂, ... sulla superficie del primo, secondo, ... conduttore, ferme restando le condizioni che V si annulli all’infinito come 1/r e che −∂V/∂r si annulli all’infinito come 1/r². Come si dimostra, la soluzione esiste, è unica e dà risultati coincidenti con quelli che si traggono dalla [2]. Se invece che i potenziali sono note le cariche dei singoli conduttori, il problema, detto allora problema di Neumann, può essere ricondotto al caso precedente calcolando, per il tramite dei coefficienti di capacità (➔ capacità), i potenziali dei conduttori.

Tecnica

Macchine elettrostatiche Dispositivi (detti anche generatori elettrostatici), capaci di operare la separazione di cariche elettriche eteronome e di creare una differenza di potenziale tra due conduttori, detti poli. La tensione tra i poli ha valori molto elevati (dalle decine di migliaia di volt delle macchine a strofinio, sino ai milioni di volt delle macchine a effluvio), ma l’intensità della corrente che se ne può ricavare è piccolissima (dell’ordine dei microampere o, al massimo, dei milliampere): si tratta dunque di generatori con forza elettromotrice molto alta e resistenza interna parimenti molto alta. Il loro uso, a parte qualche applicazione delle macchine a effluvio all’accelerazione di particelle cariche, è sostanzialmente ristretto all’ambito delle esperienze didattiche.

fig. 1

La paternità delle macchine a strofinio è attribuita a O. von Guericke. Lo schema di principio di una tale macchina è mostrato nella fig. 1: un cilindro isolante a, per esempio di vetro, è messo in rapida rotazione e strofinato sopra un cuscinetto di pelle c, cosicché si elettrizza; dalla parte opposta a c si trova un conduttore e che termina con una punta b molto vicina al cilindro. Poiché questo è carico positivamente, l’estremo lontano di e si carica, per induzione, positivamente, mentre la punta si elettrizza negativamente e la sua carica passa per effluvio sul cilindro neutralizzandone la carica positiva. All’estremo di e si ha pertanto un addensamento continuo di carica positiva che, attraverso un filo inumidito d e la terra, può tornare al cuscinetto c. Anche le macchine di J. Ramsden, di B. Le Roy, e di E. Nairne sono del tipo a strofinio.

fig. 2

Un tipico esempio di macchine a induzione è la macchina di Wimshurst (fig. 2), costituita da due dischi di ebanite a, b, paralleli, vicini, rotanti in verso opposto, su cui sono disposte molte striscioline di stagnola (settori); due coppie di pettini metallici d, d′ collegate ai poli della macchina g, g′, connessi a loro volta a due bottiglie di Leida, abbracciano i dischi agli estremi di un diametro orizzontale; infine, due coppie di spazzole fisse f, f′ ed e, e′ sfregano rispettivamente sui settori di un disco e dell’altro. Facendo ruotare i dischi ne consegue che le spazzole, per strofinio, caricano i settori, i quali, attraverso i pettini metallici, caricano con segno opposto i condensatori costituiti dalle bottiglie di Leida, e con esse i poli della macchina. La macchina può arrivare a fornire una tensione massima di qualche centinaio di migliaia di volt. Di questo tipo sono anche le macchine di R. Voss, di W. Holtz e il duplicatore di Belli.

fig. 3

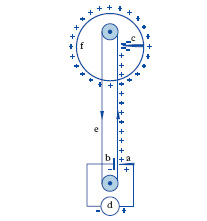
Le macchine a effluvio costituiscono il tipo di gran lunga più potente di macchina elettrostatica, ideato da R.J. Van de Graaff (1933). Mediante un generatore ad alta tensione d si stabilisce (fig. 3) tra la punta a e il piatto b una differenza di potenziale sufficiente a determinare l’effluvio; tra a e b scorre un nastro e di materiale dielettrico, che si carica positivamente; quando il nastro passa davanti alla punta c, connessa a una grande sfera metallica f, questa si carica, per induzione, positivamente, mentre la carica negativa della punta sfugge per effluvio e neutralizza quella del nastro. Mantenendo il nastro in continua rotazione mediante un motore, si può portare la sfera f a un potenziale positivo molto elevato; si possono ottenere tensioni che raggiungono diversi milioni di volt e correnti fino a qualche milliampere.