polarizzazione

Ogni processo in seguito al quale si manifesta una qualche polarità elettrica o magnetica in un corpo, un sistema di corpi ecc.: p. elettrica di un dielettrico, di un sistema elettrochimico ecc.; p. magnetica di un corpo ecc. Per estensione, qualunque processo in seguito al quale un ente fisico presenta una proprietà che individua una orientazione privilegiata: p. della luce, p. di onde, p. di particelle; lo stesso termine, opportunamente specificato, indica anche la grandezza fisica che quantifica tale proprietà.

P. elettrica

Nel suo più ampio significato, in riferimento al manifestarsi di cariche elettriche dell’uno o dell’altro segno, p. elettrica equivale a elettrizzazione (➔ elettricità); accanto a questo significato generico, si hanno vari significati particolari. Così, oltre alla p. elettrica che si manifesta in elettroliti, comunemente più nota come p. elettrolitica, la p. elettrica (o anche p. dielettrica) indica, specificamente, il complesso di fenomeni in virtù dei quali si manifestano cariche superficiali e di volume (cariche di p.) in un dielettrico immerso in un campo elettrico; tali fenomeni consistono, microscopicamente, nel manifestarsi attraverso deformazioni (p. per deformazione) di cariche dipolari negli atomi (p. elettronica) e nelle molecole (p. atomica) del dielettrico, nonché nell’orientamento dei momenti dipolari propri delle molecole ad allinearsi con il campo polarizzante (p. per orientamento): lo stato risultante è descritto da una grandezza vettoriale, detta intensità di p., o anche, semplicemente, polarizzazione.

La locuzione p. elettrolitica indica l’insorgere di polarità elettriche, cioè, in concreto, di forze controelettromotrici (forze elettromotrici di p.), in una soluzione elettrolitica in seguito a passaggio di corrente attraverso di essa; la locuzione si usa anche per indicare il complesso di fenomeni che determinano la p. stessa. Se si considerano due elettrodi immersi in un elettrolita adatto, contenuto in una cella, e si applica a questa una conveniente tensione continua, quando la tensione applicata non raggiunge un valore determinato si può verificare al più un istantaneo passaggio di corrente, dopo di che il processo si arresta poiché la prima conseguenza del fenomeno è la carica dei due condensatori elementari cui si possono assimilare le coppie anodo-elettrolita ed elettrolita-catodo. La corrente impiegata per la carica dei suddetti condensatori va sotto il nome di corrente non faradica e la modificazione del potenziale di un elettrodo a essa corrispondente è appunto una forma di polarizzazione. È pertanto evidente che, per realizzare un passaggio permanente di corrente attraverso una cella, la tensione applicata deve superare la somma delle due forze controelettromotrici che si originano rispettivamente al catodo e all’anodo, cioè la somma della p. anodica e della p. catodica: la tensione in eccesso rispetto alla suddetta somma serve a vincere la resistenza ohmica dell’elettrolita. Si noti che la tensione necessaria per far proseguire l’elettrolisi per una data densità di corrente non resta in genere costante durante tutto il periodo di funzionamento di una cella, ma di norma tende a crescere, giacché il potenziale di un elettrodo è influenzato dalla composizione dell’elettrolita a immediato contatto con esso. Così, quando un metallo passa in soluzione, e quindi funziona da anodo, la concentrazione degli ioni metallici nelle immediate vicinanze dell’elettrodo risulta superiore a quella esistente in regioni che si trovano a una certa distanza dall’elettrodo stesso: ne deriva che il potenziale anodico è spostato verso valori positivi più alti. Una situazione identica, a meno del segno, si determina al catodo; qui si ha accumulo di ioni positivi (in particolare, per es., di idrogeno) che, se non possono essere deposti alla stessa velocità con cui raggiungono l’interfaccia soluzione-elettrodo, provocano uno spostamento del potenziale verso valori negativi più bassi. Il risultato di questi due fenomeni si traduce in un aumento della forza controelettromotrice globale (p. di concentrazione), il che comporta di necessità un aumento nella tensione da applicare alla cella perché l’elettrolisi possa procedere.

P. di onde

fig. 1A

fig. 2

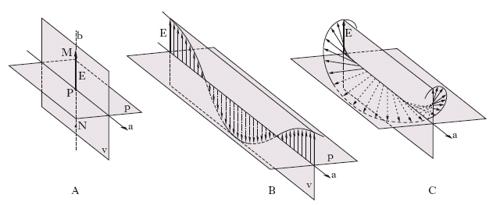
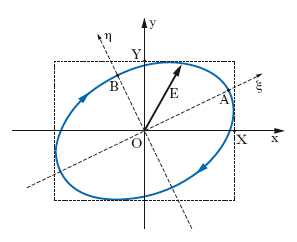
Un’onda (elastica o elettromagnetica) è caratterizzata, oltreché dalla frequenza, dal modo con cui il vettore caratteristico (lo spostamento delle particelle del mezzo nel caso di onde elastiche, l’intensità del campo elettrico o magnetico nel caso di onde elettromagnetiche) varia, o, se si vuole, ‘vibra’, punto per punto lungo la direzione di propagazione: è in base al modo di ‘vibrare’ che le onde si dividono, com’è ben noto, in longitudinali e trasversali, il vettore caratteristico vibrando parallelamente alla direzione di propagazione per le prime, ortogonalmente a quella direzione per le seconde. Mentre nel caso di onde longitudinali la direzione di vibrazione coincide con quella di propagazione, e l’onda è quindi completamente determinata, nel caso di onde trasversali per avere la completa determinazione occorre conoscere lungo quale direzione, tra le infinite ortogonali, in un punto, alla direzione di propagazione, vibra il vettore caratteristico. Il caso più semplice è quello in cui tale vettore (E in fig. 1A) vibri, in un punto P della direzione di propagazione a, costantemente secondo una determinata direzione, b: l’onda si dice essere dotata di p. rettilinea (o lineare), o anche polarizzata rettilineamente (o linearmente), il termine p. stando a significare la particolare determinazione della direzione di vibrazione tra le infinite possibili e la qualifica di ‘rettilinea’ essendo in relazione con la circostanza che, com’è evidente, l’estremo libero del vettore descrive in un intervallo di tempo pari al periodo dell’onda (supposta armonica), un segmento rettilineo MN (fig. 1A). Il piano v individuato da a, b si dice piano di vibrazione (nel punto P); il piano di p., p, è quello ortogonale al precedente e contenente la direzione di propagazione. Se il mezzo in cui avviene la propagazione è omogeneo e isotropo, accade generalmente che, se un’onda è polarizzata linearmente in un punto, essa è polarizzata linearmente ovunque: la situazione che si ha per un’onda siffatta nel generico istante è schematizzata, per un’onda armonica, nella fig. 1B, in cui p è il piano di p., v il piano di vibrazione. In questo caso, la determinazione dell’onda è completa ove sia nota la giacitura del piano di polarizzazione. Può peraltro accadere, e ciò accade in mezzi non omogenei o in mezzi dotati di potere rotatorio, che il piano di vibrazione, e con esso quello di p., vari lungo la direzione di propagazione che si considera (fig. 1C); perché l’onda sia determinata, occorre allora conoscere il modo con il quale varia la giacitura del piano in questione. A prescindere da queste eventuali variazioni introdotte dal mezzo, si può subito osservare che un’onda trasversale semplice, cioè derivante da un singolo modo di vibrazione (nel linguaggio delle onde elastiche) o da un atto elementare di emissione (nel linguaggio delle onde elettromagnetiche), è polarizzata linearmente; i casi di p. più complessa, non rettilinea, che si riscontrano sperimentalmente, si hanno quando si ha a che fare con una propagazione ondosa costituita da più onde semplici: circostanza che ricorre molto frequentemente nella pratica, e che anzi è normale per le radiazioni elettromagnetiche. Si consideri al riguardo il caso, semplice ma significativo, di un’onda che derivi dalla sovrapposizione di due onde armoniche della stessa pulsazione, ω, procedenti lungo la stessa direzione e polarizzate in piani ortogonali tra loro. Assumendo come riferimento un triedro cartesiano con origine nel generico punto O della direzione di propagazione, coincidente con l’asse z, orientato in modo che gli assi x, y coincidano con la direzione di vibrazione dell’una e dell’altra onda rispettivamente, è agevole mostrare che l’estremo libero del vettore E, caratteristico dell’onda risultante, descrive in tal caso nel piano xy un’ellisse (fig. 2) con centro in O e assi ξ e η (generalmente non coincidenti con x, y), inscritta nel rettangolo di lati 2X, 2Y, essendo X e Y le ampiezze delle onde componenti, e l’onda risultante si dice polarizzata ellitticamente. Il piano di vibrazione e quello di p. ruotano, con la frequenza dell’onda, intorno alla direzione di propagazione. Lo stato di p. è completamente determinato dall’ellisse anzidetta (ellisse di p.), che a sua volta è essenzialmente determinata dalla differenza tra le fasi iniziali, Δϕ = ϕ₂−ϕ₁, e dal rapporto tra le ampiezze, Y/X, delle due onde componenti. Se Δϕ è pari a zero o a un multiplo intero di π, l’ellisse degenera in un segmento (percorso due volte in un periodo), cioè si ha p. lineare dell’onda risultante; se Δϕ è pari a un multiplo dispari di π/2, gli assi ξ, η coincidono con gli assi x, y, rispettivamente. In quest’ultimo caso, se le ampiezze delle due onde sono uguali l’ellisse si riduce a una circonferenza e si ha p. circolare. Il verso secondo il quale l’estremo libero del vettore caratteristico descrive l’ellisse di p. è determinato dal segno della quantità sen Δϕ: precisamente, secondo una convenzione generalmente accettata, a seconda che sen Δϕ sia positivo oppure negativo si parla di p. destra oppure sinistra, il vettore caratteristico ruotando, se osservato in direzione opposta a quella di propagazione, nel verso orario oppure antiorario rispettivamente (nella fig. 2 si è assunto 0< Δϕ <π/2, e si immagina appunto di guardare nel verso di provenienza della radiazione). Quanto sinora detto può essere esteso senza difficoltà al caso in cui a sovrapporsi siano più di due onde della stessa frequenza, anche se polarizzate in piani diversi (in questo ultimo caso, basta pensare, come sempre si può fare, che ciascuna onda risulti dalla composizione di due onde polarizzate in piani ortogonali). Vale la pena di sottolineare che la p. è fenomeno esclusivo di onde trasversali, e pertanto il manifestarsi di fenomeni di p. è una prova sicura della trasversalità delle onde che li manifestano.

P. di radiazioni elettromagnetiche e p. ottica

fig. 3

Una radiazione elettromagnetica è descrivibile come una moltitudine di onde, o di treni di onde, polarizzate linearmente (secondo una convenzione pressoché generale, per un’onda elettromagnetica si assume come vettore caratteristico l’intensità del componente elettrico del campo elettromagnetico, di modo che il piano di vibrazione è quello che contiene tale vettore, mentre il piano di p. è quello che contiene il vettore magnetico, ortogonale, come si sa, al precedente vettore elettrico). Tali onde elementari, derivanti ciascuna da un atto elementare di emissione, possono avere la stessa direzione di propagazione, eventualmente la stessa ampiezza, eventualmente ancora (se la radiazione è monocromatica) la stessa frequenza, ma generalmente non hanno lo stesso piano di p. né una ben definita relazione di fase; la situazione, in generale, è quella schematizzata nella fig. 3: nel generico punto P della direzione di propagazione a e al generico istante, non v’è una direzione di vibrazione privilegiata, le vibrazioni dei vettori delle singole onde avvenendo, con uguale probabilità statistica, in tutte le direzioni ortogonali ad a e con tutti i possibili valori per le fasi iniziali (o anche per le fasi istantanee se la radiazione è policromatica). Poiché i tempi d’osservazione, per quanto brevi, sono in genere molto lunghi rispetto all’intervallo di tempo con cui mediamente si succedono gli atti elementari d’emissione, le singole onde elementari non sono separabili, e i fenomeni che si possono osservare riguardano un numero sempre molto grande di onde elementari. Una radiazione per la quale valga la situazione della fig. 3 è detta non polarizzata, o anche naturale per significare che questo è lo stato delle radiazioni conseguenti agli ordinari processi di irraggiamento (➔) elettromagnetico. Può accadere però che questa naturale mancanza di piani di vibrazioni privilegiati venga meno, nel senso che una parte più o meno grande delle onde elementari risulti polarizzata nello stesso piano: la radiazione si dice allora parzialmente polarizzata. Come si è ricordato, la generalità delle sorgenti elettromagnetiche, e in particolare luminose, emette radiazioni non polarizzate; queste però possono acquistare una p. più o meno elevata sia spontaneamente, in conseguenza di certi fenomeni di propagazione, sia perché forzate a passare in un polarizzatore. Non va tuttavia dimenticata l’esistenza di sorgenti che, in virtù di loro particolari meccanismi d’irraggiamento, emettono radiazioni totalmente polarizzate: è il caso dei dipoli hertziani e in genere delle antenne radiotrasmittenti (un’antenna a dipolo emette una radiazione costituita da onde coerenti, tutte polarizzate in un periodo ortogonale all’asse del dipolo).

fig. 4

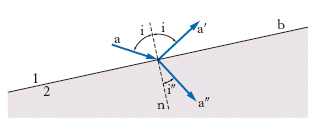
P. per riflessione e per rifrazione. - La radiazione elettromagnetica, costituita da onde piane monocromatiche, che incide sulla superficie di separazione tra due mezzi diversi, 1 e 2 omogenei e isotropi, viene in parte riflessa in parte rifratta. Facendo riferimento, come per semplicità si usa fare, ai raggi di propagazione e non ai fronti d’onda, un raggio a (fig. 4) dà luogo, incidendo sulla superficie b, a un raggio riflesso a′ e a un raggio rifratto a″; secondo le leggi della riflessione e della rifrazione, i due angoli di incidenza e di riflessione hanno lo stesso valore i e, detto i″ l’angolo di rifrazione (in fig. 4, n è la normale a b nel punto in cui incide a), vale la relazione sen i/sen i″=n₁₂, essendo n₁₂ l’indice di rifrazione del mezzo 2 rispetto al mezzo 1. Si consideri ora una qualunque delle onde elementari (polarizzate linearmente) che incidono su b, e le corrispondenti onda riflessa e onda rifratta; si pensi di scomporre, com’è sempre possibile fare, il vettore elettrico di ognuna di queste tre onde nei due componenti parallelo e ortogonale rispetto al piano d’incidenza (determinato da a, n); indicando con il simbolo p il componente parallelo, con o quello ortogonale, si hanno complessivamente le sei componenti E_p, E_o (onda incidente), E_p′, E_o′ (onda riflessa), E_p″, E_o″ (onda rifratta). Com’è chiaro, tale scomposizione equivale, per ognuna delle onde, a considerare onde componenti polarizzate linearmente in un piano ortogonale al piano d’incidenza (componenti paralleli) e in un piano parallelo a quello (componenti ortogonali). Se si impongono le condizioni di continuità dettate dall’elettromagnetismo per il passaggio attraverso la superficie di separazione dei due mezzi (continuità dei componenti tangenziali delle intensità elettrica e magnetica, continuità dei componenti normali delle induzioni elettrica e magnetica), risulta (➔ riflessione; rifrazione) che i rapporti E_p′/E_o′ e E_p″/E_o″ sono in genere diversi dal rapporto E_p/E_o; ciò significa che, a seconda delle circostanze (precisamente, a seconda del valore degli angoli di incidenza e di rifrazione), una componente viene riflessa o rifratta meglio dell’altra: la riflessione e la rifrazione introducono quindi una certa p. (per i ≠0). Si osservi al riguardo che risulta essere sempre E_p″/E_o″>E_p/E_o: così, la rifrazione favorisce i componenti paralleli al piano d’incidenza di modo che il raggio rifratto, arricchito per così dire di tali componenti, è parzialmente polarizzato (piano di vibrazione parallelo al piano d’incidenza, piano di p. ortogonale a esso). Il contrario accade per la riflessione, che dà luogo a una p. parziale ortogonale a quella della rifrazione. In particolare, se è verificata la cosiddetta condizione di Brewster, i+i″=π/2 (perpendicolarità tra raggio riflesso e raggio rifratto, come in fig. 4), risulta E′=0: delle onde elementari incidenti vengono riflesse le sole componenti il cui vettore vibra ortogonalmente al piano d’incidenza, cosicché il raggio riflesso è totalmente polarizzato, con piano di p. parallelo al piano d’incidenza. Se si indica con i_B l’angolo di Brewster (o angolo di incidenza brewsteriana), cioè l’angolo che soddisfa la condizione data, con facili calcoli si trova per esso il valore i_B=arctg n₁₂. Una superficie riflettente è dunque, sotto incidenza brewsteriana, un polarizzatore per riflessione: essa trasforma una radiazione (per es., un fascio di luce) naturale incidente in una radiazione riflessa totalmente polarizzata. Una superficie del genere ha inoltre un’importante proprietà: in quanto capace di riflettere soltanto onde polarizzate linearmente in un piano a essa ortogonale, quando viene investita da una radiazione linearmente polarizzata essa presenta per questa radiazione un coefficiente di riflessione che è massimo quando il piano di p. della radiazione è ortogonale a essa, minimo, e precisamente nullo, quando tale piano è parallelo.

P. per doppia rifrazione e per pleocroismo. - Particolarmente netti, e particolarmente importanti per le applicazioni ottiche, sono i fenomeni di p. che si verificano quando una radiazione attraversa un mezzo birifrangente (un cristallo monoassico o biassico, un plasma ecc.). Si ricordi che un mezzo del genere è caratterizzato dal fatto che la velocità di propagazione e il coefficiente d’assorbimento per onde elettromagnetiche propagantisi in esso dipendono non soltanto, come nei mezzi ordinari, dalla frequenza delle onde, ma anche dalla direzione di vibrazione del vettore elettrico, e precisamente dalla giacitura del piano di vibrazione rispetto a un certo piano caratteristico del mezzo in questione. Accade così che i due fasci polarizzati (in piani ortogonali tra loro), di cui si può immaginare costituito un fascio incidente non polarizzato, siano diversamente rifratti (➔ birifrangenza) e siano diversamente assorbiti (➔ pleocroismo): circostanze queste che determinano una certa p. del fascio emergente. Se, con opportuni artifici, si riesce a raccogliere uno solo dei due fasci, all’uscita dal mezzo si ha una radiazione totalmente polarizzata in un piano a seconda dei casi parallelo oppure ortogonale rispetto all’anzidetto piano caratteristico del mezzo birifrangente.

fig. 5

P. per diffusione. - Esaminando con un analizzatore la radiazione c (fig. 5), diffusa da un mezzo diffondente b investito da un fascio di radiazione non polarizzata a, si trova che essa è parzialmente polarizzata, con direzione di vibrazione ortogonale al piano di diffusione d determinato da a, c. Ciò accade in quanto anche la diffusione, come la riflessione e la rifrazione, dà luogo a polarizzazione. Precisamente, se le particelle diffondenti hanno dimensioni non molto grandi, per modo che si abbia diffusione (➔) alla Rayleigh, si trova che l’ampiezza del componente dell’onda diffusa ortogonale al piano di diffusione non dipende dall’angolo di diffusione ϑ, mentre per il componente parallelo a tale piano l’ampiezza è proporzionale a cosϑ; ne segue che, se si raccoglie la radiazione diffusa nella stessa direzione di quella incidente (diffusione in avanti oppure all’indietro), in modo che sia cosϑ=±1, i due componenti anzidetti hanno uguale ampiezza e la radiazione non è polarizzata, mentre se si raccoglie la radiazione diffusa ortogonalmente (ϑ=π/2, 3π/2, cosϑ=0), si trovano per essa soltanto componenti ortogonali al piano di diffusione. In tali ultime condizioni la radiazione dovrebbe essere totalmente polarizzata in un piano parallelo a quello di diffusione: ciò in realtà non accade quasi mai, a causa di diffusioni non alla Rayleigh subite dalla radiazione, e si ha quindi soltanto una più o meno spinta p. parziale. Si ricorda che a questo fenomeno è in particolare dovuta la p. parziale della luce diurna, cioè della luce solare diffusa dall’atmosfera terrestre (➔ cielo).

P. rotatoria. Con questa locuzione si indica talora il potere rotatorio delle sostanze otticamente attive, cioè la capacità che alcune sostanze hanno, naturalmente oppure in particolari condizioni fisiche, di far rotare il piano di p. di una radiazione polarizzata che si propaghi in esse.

P. di particelle

Come per le radiazioni elettromagnetiche o per perturbazioni elastiche ondose, anche per i fasci di particelle (cioè per le radiazioni corpuscolari) può accadere che la propagazione avvenga in particolari condizioni di ‘ordine’; per analogia con il caso delle altre radiazioni, si dà a questo fenomeno il nome di polarizzazione. Precisamente, un fascio di particelle si dice parzialmente polarizzato se vi è una direzione lungo la quale risultano preferenzialmente allineati i momenti della quantità di moto intrinseca, cioè gli spin, delle particelle; totalmente polarizzato se tutti gli spin risultano ugualmente orientati. Nel formalismo della meccanica quantistica l’assenza di p. corrisponde alla circostanza che tutti gli stati di spin possibili per le particelle sono ugualmente probabili, laddove la p., più o meno spinta, corrisponde all’esistenza di stati più probabili di altri: la determinazione dello stato di p. corrisponde dunque alla determinazione delle probabilità competenti ai vari stati possibili per le particelle costituenti la radiazione in esame. Poiché di una radiazione elettromagnetica può essere data anche una descrizione in termini di fotoni, la p. di un fascio di tali radiazioni può essere attribuita anche all’orientamento degli spin dei fotoni che costituiscono il fascio. Fenomeni di p. si accompagnano in genere ai fenomeni con cui le particelle interagiscono con la materia o tra loro (per es., fenomeni di diffusione); da questi fenomeni, opportunamente provocati in dispositivi che (per analogia con quelli usati in ottica) hanno il nome di polarizzatori e analizzatori, si determina sperimentalmente lo stato di p. di una radiazione. Poiché il momento magnetico delle particelle elementari che ne sono dotate è parallelo (o antiparallelo) allo spin, la p. può essere ottenuta sottoponendo le particelle a opportuni campi magnetici che tendono ad allinearne i momenti magnetici. Così fasci di elettroni o di protoni parzialmente polarizzati si hanno negli anelli di accumulazione, a causa della lunga permanenza delle particelle in campi magnetici molto intensi.

P. del vuoto

Per il principio di indeterminazione di Heisenberg e di equivalenza massa-energia, in qualunque punto dello spazio vuoto sono presenti coppie virtuali particella-antiparticella, ciascuna per un tempo sufficientemente breve (Δt<h/mc², con h costante di Planck, m massa della particella e c velocità della luce nel vuoto); la presenza di un campo di forza deforma la distribuzione delle cariche delle particelle virtuali dando origine alla p. del vuoto. Nel caso dell’elettrodinamica quantistica (➔ elettrodinamica), nei dintorni di una carica elettrica puntiforme q, a distanza r sufficientemente piccola ove il campo elettrico è più intenso, le coppie virtuali elettrone-positrone sono polarizzate dal campo elettrico della carica stessa; si dimostra che gli effetti della nuvola di dipoli e⁺e^– virtuali si manifestano in una regione intorno alla carica q di dimensioni dell’ordine della lunghezza d’onda Compton dell’elettrone λ_e=h/m_ec (con m_e massa dell’elettrone): il campo elettrico generato da q è in questa regione descrivibile o mediante un potenziale coulombiano V(r)=q/4πε₀ε_rr, con una costante dielettrica relativa ε_r funzione crescente di r, o ponendo ε_r=1 e sommando al potenziale coulombiano un termine correttivo (termine di Uheling, decrescente esponenzialmente con r/λ_e). W.E. Lamb, all’inizio degli anni 1950, ha dimostrato sperimentalmente, misurando accuratamente la differenza di energia (spostamento di Lamb o Lamb shift) tra i livelli 2S e 2P nell’atomo di idrogeno, l’esistenza della correzione di Uheling, confermata successivamente da misurazioni su atomi muonici.

Polarizzatori

Genericamente, si chiama polarizzatore ogni dispositivo atto a polarizzare radiazioni luminose o più in generale elettromagnetiche. A seconda del fenomeno in virtù del quale si produce in esso la p. delle radiazioni incidenti, si parla di polarizzatori a riflessione, a rifrazione, a birifrangenza.

I polarizzatori a riflessione sfruttano la p. che si produce nella riflessione; sono solitamente costituiti da una o più lastre di vetro sulle quali la luce viene fatta successivamente riflettere sotto incidenza brewsteriana.

I polarizzatori a rifrazione sfruttano la p. parziale che s’accompagna alla rifrazione.

fig. 6A

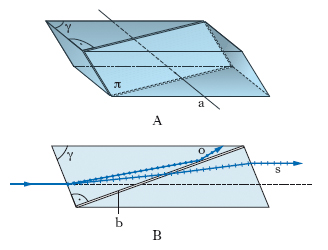
I polarizzatori a birifrangenza, i più usati, sfruttano le proprietà dei cristalli birifrangenti. A seconda dell’artificio cui si ricorre per eliminare uno dei due raggi polarizzati cui dà luogo la birifrangenza, si distinguono polarizzatori a prisma e a pleocroismo. Il più importante polarizzatore a birifrangenza a prisma è brevemente detto nicol, dal nome dell’ideatore (1828) W. Nicol, ed è costituito da un prisma di calcite, tagliato secondo il piano diagonale π, ortogonale all’asse ottico a (fig. 6A) in due parti, incollate poi insieme con balsamo del Canada, il cui indice di rifrazione è intermedio fra gli indici dei raggi ordinario e straordinario nella calcite. Le facce laterali del prisma corrispondono a quattro facce del romboedro di sfaldatura, mentre le facce di base sono ricavate artificialmente e lavorate in modo che l’angolo γ sia di 68° (l’angolo di sfaldatura naturale è di 71°). Il prisma è, di solito, annerito lateralmente e racchiuso in una guaina metallica che lascia libere le sole facce terminali. L’inclinazione del piano diagonale è tale che, dei due raggi rifratti e polarizzati rettilineamente a 90° tra loro, che si producono quando la luce penetra nel prisma sotto un angolo (fig. 6B) non maggiore di 14°, solamente il raggio straordinario s può attraversare lo strato di balsamo b e quindi emergere nell’aria, mentre il raggio ordinario o viene eliminato perché, dopo aver subito la riflessione totale su b, è assorbito dal rivestimento nero laterale: dal polarizzatore emerge pertanto un solo raggio, lo straordinario, totalmente polarizzato in un piano (piano di p. del nicol). Quest’ultimo, a seconda del tipo di polarizzatore, è ortogonale oppure parallelo al piano della fig. 6B, cioè alla cosiddetta sezione principale e la cui intensità è poco meno della metà di quella della luce naturale incidente. Se si invia un fascio di luce naturale di intensità I₀ su un nicol (polarizzatore) e si esamina successivamente la luce emergente mediante un secondo nicol (analizzatore), per l’intensità della luce emergente dal secondo nicol si ha: I≅I₀(cos²α)/2, indicando con α l’angolo formato dalle sezioni principali dei due nicol; I/I₀ è massimo per α=0° (nicol paralleli), minimo per α=90° (nicol incrociati). Il nicol è un ottimo polarizzatore per tutto lo spettro visibile e per parte dello spettro infrarosso e ultravioletto. I polarizzatori pleocroici (in particolare dicroici), sfruttano la circostanza che nelle sostanze birifrangenti con apprezzabile dicroismo o tricroismo uno dei due raggi polarizzati cui dà luogo un raggio incidente di luce non polarizzata è assorbito più dell’altro (➔ pleocroismo); così, se lo spessore della sostanza è sufficiente, emerge da essa solo il raggio meno assorbito. Un polarizzatore dicroico, un tempo piuttosto usato, è quello a tormalina, costituito semplicemente da una laminetta di tormalina, tagliata parallelamente all’asse ottico e spessa qualche millimetro: tale spessore è sufficiente perché il raggio ordinario sia completamente assorbito, talché emerge il solo raggio straordinario. Poiché il dicroismo (o il tricroismo) è fortemente selettivo, la luce trasmessa dai polarizzatori pleocroici è colorata (quella trasmessa dalla tormalina, per es., è verde), il che limita l’impiego di tali dispositivi. Questo inconveniente non esiste nei polarizzatori pleocroici artificiali noti con il nome di polaroidi, costituiti da un sottile conglomerato di cristallini di herapathite, ugualmente orientati, e di un legante plastico trasparente: essi non alterano sensibilmente lo spettro della luce che li attraversa. Notevolissimi vantaggi dei polaroidi sono il loro prezzo (al loro confronto, i nicol e i polarizzatori del tipo dei nicol sono assai costosi) e la possibilità di realizzare con essi polarizzatori di grandi dimensioni, con sezioni utili dell’ordine di centinaia di cm² (la sezione utile dei nicol più grandi è dell’ordine di qualche cm²); questi vantaggi, che compensano la minore trasparenza, giustificano l’ampio uso dei polaroidi nelle applicazioni tecniche.