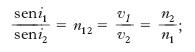rifrazione

Fenomeno ottico (detto anche r. ordinaria o semplice) consistente nella deviazione che raggi luminosi generalmente subiscono nel passare dall’uno all’altro di due mezzi trasparenti diversi, per es., dall’aria all’acqua; trae il suo nome dal fatto che un oggetto immerso in parte in un mezzo, in parte nell’altro (per es., un bastone infilato in parte nell’acqua) appare come se fosse piegato, spezzato. Sempre nell’ambito dell’ottica, si chiama genericamente r. anche il fenomeno per cui raggi luminosi percorrono traiettorie curve, anziché rettilinee, propagandosi in un mezzo omogeneo quanto alla natura ma non omogeneo quanto alle caratteristiche ottiche, per es., in un mezzo la cui densità vari regolarmente in una certa direzione: è la cosiddetta r. continua, di cui un notevole esempio è dato dall’incurvamento che raggi luminosi subiscono nell’atmosfera terrestre (r. atmosferica).

Come nel caso della riflessione, la r. si presenta come un fenomeno generale di propagazione di energia per onde e di essa può essere fatta una teoria generale valida per qualunque tipo di perturbazione ondosa, con una formulazione specifica per le onde elettromagnetiche (valida, come casi particolari, per il calore raggiante, la luce, le radioonde ecc.) e per le onde elastiche. Si parla anche di r. di particelle, e in particolare di r. di elettroni, per indicare il particolare comportamento, per molti versi riconducibile a quello di un fascio luminoso in un mezzo con costanti ottiche variabili, presentato da un fascio di particelle cariche in un campo elettrico o magnetico non uniforme. Con estensione puramente analogica, il termine è infine usato per indicare la deviazione che le linee di forza di un campo elettrico o di un campo magnetico generalmente subiscono nel passaggio attraverso la superficie di separazione tra due mezzi diversi (r. elettrica, magnetica).

La proprietà di una sostanza o di un mezzo materiale in genere di rifrangere la luce, i suoni ecc. è detta rifrangenza.

R. atmosferica

È l’incurvamento che raggi luminosi, radioonde ecc., e anche suoni e onde longitudinali elastiche in genere, subiscono nell’atmosfera terrestre: si tratta di una r. continua, dovuta al fatto che l’indice di r. atmosferico (per la luce, le radioonde, i suoni ecc.) non è costante, in genere variando, più o meno regolarmente, con l’altezza sul suolo.

fig. 1

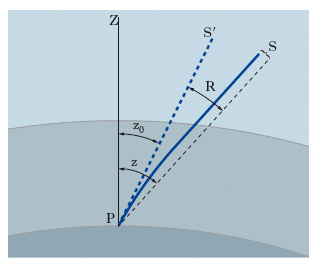
Tale fenomeno, cui, per es., è dovuto il ‘miraggio ottico’, ha particolare rilevanza in astronomia, disciplina nella quale la locuzione r. atmosferica ha un significato specifico, indicando, oltre al fenomeno, anche una conseguenza quantitativa del fenomeno medesimo, e precisamente un termine correttivo che va aggiunto alla distanza zenitale osservata di un astro per avere la distanza zenitale effettiva. Precisamente, a causa dell’incurvamento che i raggi luminosi provenienti da un astro subiscono nell’attraversare l’atmosfera terrestre, un osservatore P vede l’astro medesimo, sulla volta celeste, nella posizione apparente S′anziché nella vera posizione S (fig. 1: l’effetto è stato esagerato per motivi di chiarezza). Poiché, a meno di trascurabili irregolarità locali, l’indice di r. dell’atmosfera per i raggi luminosi varia soltanto con la quota, il fenomeno si svolge con simmetria sferica rispetto al centro della Terra e la traiettoria dei raggi è interamente contenuta nel piano contenente l’astro S, l’osservatore P e lo zenit Z del luogo d’osservazione: la r. atmosferica ha quindi per effetto di alterare solo la distanza zenitale dell’astro, l’azimut di questo restando immutato. L’indice di r. ottico dell’atmosfera dipende essenzialmente dalla densità e decresce procedendo dal suolo verso l’alto; l’incurvamento dei raggi è tale che la distanza zenitale osservata z₀ dell’astro è leggermente minore di quella vera, z: quest’ultima si ottiene aggiungendo a z₀ una quantità positiva, R, detta appunto r. atmosferica per l’astro osservato: z=z₀+R. La r. atmosferica R è nulla se l’astro è allo zenit e cresce al crescere della distanza zenitale; varia leggermente al variare della temperatura t e della pressione p che si hanno nel luogo d’osservazione. La r. atmosferica normale, cioè il valore R₀ di R per condizioni normali di temperatura e di pressione vale circa 22″ per z₀=20°, ca. 50″ per z₀=40°, ca. 1′44″ per z₀=60°. Per distanze zenitali maggiori di 75° il valore di R non è calcolabile con sufficiente approssimazione, per cui gli astronomi evitano di fare misurazioni relative ad astri poco alti sull’orizzonte. È interessante notare che la r. orizzontale, cioè per astri all’orizzonte, è mediamente di 36′36″; così, un astro sembra che sia all’orizzonte quando in realtà è circa mezzo grado al di sotto di esso; di questo fatto occorre naturalmente tener conto per il calcolo esatto dell’istante del nascere e del tramontare degli astri.

R. elettrica

fig. 2

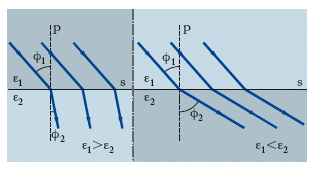
Il fenomeno (detto anche r. dielettrica) in virtù del quale le linee di forza di un campo elettrico subiscono una deviazione in corrispondenza alla superficie di separazione tra due dielettrici di natura diversa. Considerando, per semplicità, una superficie piana s di separazione fra due dielettrici omogenei e isotropi, aventi costante dielettrica assoluta ε₁ e ε₂ rispettivamente, il campo elettrico nel secondo mezzo ha direzione generalmente diversa da quella del campo nel primo mezzo (fig. 2). Imponendo le appropriate condizioni di continuità attraverso s ai vettori del campo (continuità della componente del vettore intensità parallela a s, continuità della componente del vettore induzione normale a s), per gli angoli ϕ₁ e ϕ₂ indicati in fig. 2, che caratterizzano la r. delle linee di forza attraverso s, si trova la relazione: ε₁tgϕ₂=ε₂tgϕ₁; in luogo delle costanti dielettriche assolute possono essere considerate le corrispondenti costanti dielettriche relative. Il rapporto ε₁/ε₂ è detto indice di r. elettrica del dielettrico 2 rispetto al dielettrico 1; a seconda che tale indice sia maggiore oppure minore dell’unità, le linee di forza nel secondo dielettrico si accostano oppure si allontanano dalla normale p a s. La relazione ora ricordata ha delle analogie con la seconda legge della r. ottica, ma mentre nella legge della r. ottica gli angoli caratteristici compaiono come argomenti di seni, qui compaiono come argomenti di tangenti, il che porta a escludere nella r. elettrica la possibilità di un fenomeno analogo alla riflessione totale nella r. ottica.

R. magnetica

Fenomeno consistente in una deviazione che le linee di forza di un campo magnetico subiscono nell’attraversare la superficie di separazione tra due mezzi aventi permeabilità magnetica diversa. È formalmente analogo alla r. elettrica e si tratta allo stesso modo, facendo corrispondere alle costanti dielettriche (assolute o relative) le permeabilità magnetiche (assolute o relative) dei due mezzi, μ₁ e μ₂; vale lo schema geometrico della fig. 2, e si ha: μ₁tgϕ₂=μ₂tgϕ₁. Al rapporto μ₁/μ₂ si dà il nome di indice di r. magnetica del mezzo 2 rispetto al mezzo 1; poco diverso dall’unità per mezzi dia- o paramagnetici, assume valori piuttosto piccoli (dell’ordine di 10^–3 e anche meno) nel caso di un campo magnetico che penetri da un mezzo dia- o paramagnetico in un mezzo ferromagnetico (per es., al passaggio aria-ferro): in questo caso, linee di forza incidenti obliquamente sulla superficie del mezzo ferromagnetico si rifrangono in questo allontanandosi fortemente dalla normale alla superficie, tendendo cioè a procedere parallelamente alla superficie medesima (è la situazione analoga a quella, elettrica, schematizzata nella fig. 2, a destra).

R. di radiazioni elettromagnetiche

Fenomeno che, insieme alla riflessione, si produce alla superficie di un mezzo limitato in cui si propaghi una radiazione elettromagnetica (in particolare, radiazione luminosa): la radiazione emergente dal mezzo in questione e propagantesi nel mezzo al di là del primo, subisce in genere un cambiamento di direzione e, inoltre, un cambiamento di intensità e di stato di polarizzazione, dipendenti sia da fattori geometrici sia dalle costanti elettromagnetiche (costante dielettrica, permeabilità, conduttività elettrica) dei due mezzi. In quel che segue ci riferiremo alla r. per discontinuità, al caso cioè in cui esista una superficie (superficie rifrangente) attraverso la quale le costanti elettromagnetiche subiscano una variazione netta, qual è la superficie che separa due mezzi diversi; al caso della r. continua, in cui cioè la variazione delle costanti sia continua su scala macroscopica, accenneremo separatamente più oltre.

fig. 3

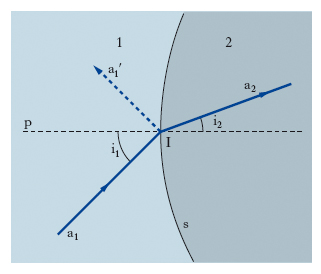
Considerando dunque la r. attraverso la superficie che separa due mezzi diversi, omogenei, isotropi e considerando, per semplicità, la r. monocromatica e quindi rappresentabile con onde armoniche, le leggi che regolano gli aspetti geometrici del fenomeno possono essere ricavate senza difficoltà, per es., applicando il principio di Huygens (➔ ottica); esse furono enunciate, per la luce, dapprima da W. Snellius per via sperimentale, poi, in maniera più rigorosa, da R. Descartes per via analitica, e sono note come leggi di Snellius-Descartes o leggi di Cartesio. La prima legge della r., analoga alla prima legge della riflessione, afferma che il raggio incidente a₁ (fig. 3), il raggio rifratto a₂ e la normale p alla superficie rifrangente s nel punto d’incidenza I giacciono nello stesso piano, detto ‘piano d’incidenza’ (in questo piano giace anche il raggio riflesso a′₁, del quale peraltro non ci occuperemo). La seconda legge della r. stabilisce poi che l’angolo d’incidenza i₁ (angolo tra a₁ e p) e l’angolo di r. i₂ (angolo tra a₂ e p) sono legati dalla relazione

[1] formula

dove la quantità n₁₂, invariabile, per le onde considerate, al variare dell’angolo di incidenza, ha il nome di indice di r. del mezzo 2 rispetto al mezzo 1, o anche di indice di r. relativo del mezzo 2 rispetto al mezzo 1 (il mezzo 1 è quello in cui si propagano le onde incidenti). Applicando il principio di Huygens, risulta n₁₂=v₁/v₂, essendo v₁, v₂ le velocità di propagazione (di fase) delle onde nell’uno e nell’altro mezzo. Chiamando indice di r. assoluto di un mezzo l’indice di r. relativo di esso rispetto al vuoto, cioè la quantità

[2] formula

dove c indica la velocità delle onde elettromagnetiche nel vuoto, la [1] può essere scritta nella forma

[1]' formula

una forma equivalente è la seguente:

[3] formula

alla costante, adimensionata, A, dandosi il nome di invariante di r. (per le onde considerate).

Restando nell’ambito delle questioni di carattere puramente geometrico, da quanto detto risulta che per incidenza normale (i₁=0) l’angolo di r. è nullo, cioè i raggi non subiscono deviazione. Per incidenza obliqua (0<i₁≤π/2), se n₁₂ è maggiore dell’unità (n₂>n₁), ovvero, come si usa dire, se il mezzo 2 è più rifrangente del mezzo 1, i raggi si rifrangono accostandosi alla normale (i₂<i₁); se, invece, il mezzo 2 è meno rifrangente del mezzo 1 (n₁₂<1; n₂<n₁), i raggi si rifrangono allontanandosi dalla normale (i₂>i₁). Mentre nel primo caso si ha r. sempre, cioè qualunque sia l’angolo di incidenza i₁, nel secondo caso v’è chiaramente un valore massimo i_l, detto angolo limite di r., per i₁, corrispondente al valore massimo, i₂=π/2, dell’angolo di r., superato il quale non v’è più r., tutti i raggi incidenti essendo riflessi dalla superficie rifrangente (fenomeno della riflessione totale); dalla [1] si ricava che è: i_l=arcsen n₁₂. Sperimentalmente si osserva che se si considera una certa coppia di mezzi e si varia la frequenza delle onde, si ottengono di volta in volta valori diversi per l’indice di r. n₁₂; ciò significa che se si opera con una radiazione policromatica, a un raggio incidente obliquamente sulla superficie rifrangente corrispondono tanti raggi rifratti in direzioni diverse quante sono le radiazioni monocromatiche componenti: queste ultime, tutte unite nel raggio incidente, risultano separate, disperse dopo essere state rifratte, e ciò costituisce il fenomeno della dispersione per r. (➔ dispersione).

R. della luce

tab. 1

tab. 2

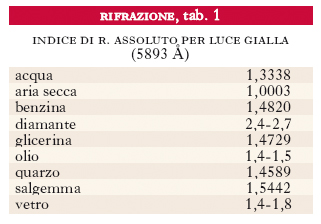
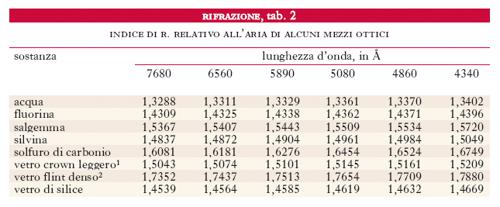
Il fenomeno della r. e lo studio sia geometrico sia analitico delle sue modalità è stato storicamente condotto con riferimento a onde luminose. Ancor oggi, quando, per es., si parla di indice di r. di un mezzo, senza ulteriori specificazioni, ci si riferisce sempre all’indice di r. per la luce. Nella tab. 1 sono riportati i valori dell’indice di r. assoluto, per la luce gialla del sodio (5893 Å) di varie sostanze (quelle solide e liquide, a temperatura di 20 °C; quelle aeriformi, in condizioni normali di temperatura e di pressione); nella tab. 2 sono i valori dell’indice di r. relativo all’aria (pochissimo diverso, peraltro, da quello assoluto), per varie lunghezze d’onda, di alcuni mezzi trasparenti usati in ottica.

Se la luce è bianca, o genericamente non monocromatica, alla r. s’accompagnano, più o meno vistosamente, fenomeni di dispersione (o cromatismo per r.), in virtù dei quali, grossolanamente parlando, la luce rifratta ha caratteristiche cromatiche diverse da quelle che aveva inizialmente. Nei mezzi otticamente anisotropi la r. si presenta poi con caratteristiche speciali: vi è una sorta di sdoppiamento dei raggi e il fenomeno prende specificamente il nome di doppia r. o birifrazione (➔ birifrangenza).

Rifrattometri

Il rifrattometro è lo strumento o dispositivo usato per la misurazione dell’indice di rifrazione.

fig. 4

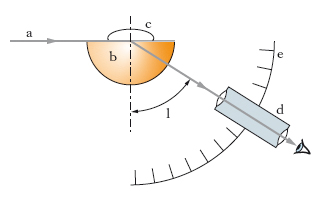
Per quanto riguarda i rifrattometri ottici, cioè usati nel campo delle radiazioni visibili, ve ne sono di vari tipi, riducibili però, come principio di funzionamento a tre: rifrattometri a dispersione, a riflessione totale, interferometrici. I rifrattometri a dispersione sono basati sul fatto che l’angolo di deviazione minima δ_m di un prisma di dato angolo rifrangente è in relazione con l’indice di r. n (relativo all’aria ambiente) del materiale di cui il prisma stesso è costituito (➔ prisma); sono schematicamente costituiti da un dispositivo che consente di misurare appunto l’angolo di deviazione minima di un campione della sostanza in esame foggiato a prisma (se la sostanza è liquida, si usa per essa un contenitore di vetro a forma prismatica). I rifrattometri a riflessione totale (o totalrifrattometri) sono basati sul fatto che l’angolo limite l per la riflessione totale nel passaggio da un mezzo di indice n₁ a uno di indice n₂ è legato agli indici stessi dalla relazione senl=n₂/n₁; noto che sia uno degli indici e misurato l, si può pertanto determinare l’altro (➔ riflessione). Poiché per la misurazione di uno dei due indici di r. occorre conoscere preventivamente l’altro, i totalrifrattometri sono degli strumenti di misurazione ‘relativi’, a differenza dei rifrattometri a dispersione che sono invece ‘assoluti’. Fra essi, molto usato è il rifrattometro a semisfera di Abbe (fig. 4), costituito da una semisfera di vetro b, di indice di rifrazione n₀ noto; un campione della sostanza in esame c, lavorato in modo che abbia una superficie piana (o una goccia di sostanza, se questa è liquida), viene appoggiato al centro della parte piana della semisfera; la superficie di contatto viene illuminata da un fascetto di luce monocromatica a e osservata a mezzo di un cannocchiale d scorrevole su un settore graduato e. Variando l’inclinazione del fascio incidente e l’orientamento del cannocchiale, si determina l’angolo limite l di riflessione totale: l’indice di r. n della sostanza in esame è allora dato dalla relazione: n=n₀senl (naturalmente, occorre che sia n<n₀). I rifrattometri interferometrici sono anch’essi strumenti relativi: la misurazione dell’indice di r. viene effettuata misurando la differenza di cammino ottico provocata dall’inserzione di uno spessore noto della sostanza in esame su uno dei due rami di un interferometro. Essi sono adatti per misurazioni su sostanze solide, liquide o aeriformi.