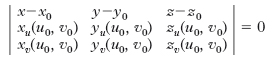superficie
superficie Il contorno di un corpo, come elemento di separazione fra la parte di spazio occupata dal corpo e quella non occupata.
Diritto
Diritto di s. Diritto di fare e mantenere al di sopra del suolo altrui una costruzione di cui si acquista la proprietà.
Introdotto nel nostro ordinamento dal codice civile del 1942, trova la sua definizione generale nell’art. 952, in base al quale il proprietario può costituire il diritto di fare o mantenere una costruzione a favore di altri che ne acquista la proprietà oppure può alienare la proprietà della costruzione già esistente, separatamente dalla proprietà del suolo. Nel primo caso, si parla anche di s. in senso stretto, o ius aedificandi (sul suolo altrui); nel secondo, si parla anche di s. in senso lato, o proprietà superficiaria. Se il diritto di s. è stato costituito a tempo determinato, si estingue (così come i diritti reali imposti dal superficiario) alla scadenza del termine e il proprietario del suolo acquista la proprietà della costruzione. Il diritto di s. può estinguersi anche per il perimento della costruzione (nel caso di specifico patto tra le parti), per prescrizione in conseguenza del non uso protratto per 20 anni, per rinuncia, per consolidazione o confusione. Per evitare ogni ostacolo al progresso agricolo il codice vigente, a differenza di quello abrogato, vieta la costituzione o il trasferimento della proprietà delle piantagioni separatamente dalla proprietà del suolo. Le disposizioni sulla s. si applicano anche nel caso in cui sia concesso il diritto di fare e mantenere costruzioni al disotto del suolo altrui.
Fisica e chimica
Fisica delle s. dei solidi cristallini
I solidi cristallini possiedono una struttura periodica in cui gli atomi sono disposti ai vertici di un reticolo ma, a causa del fatto che gli atomi di s. non rispettano la simmetria dell’interno del solido, la struttura della s. non coincide con quella di uno dei piani del reticolo del cristallo. Pertanto le proprietà delle s. dei solidi sono del tutto peculiari rispetto alle proprietà all’interno del solido e si evidenziano in fenomeni come l’emissione fotoelettrica, l’effetto termoelettronico, il chemiadsorbimento e la catalisi, l’adesione, la corrosione, il trasporto elettronico di s. ecc.
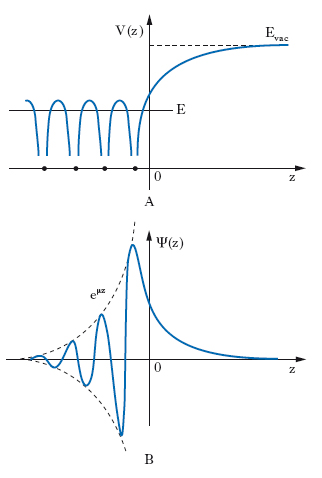
La maggiore perturbazione introdotta in un solido dall’esistenza di una s. delimitante è la rottura della simmetria traslazionale del reticolo cristallino (➔ solido). Anche per un’ipotetica s. ideale, con gli atomi superficiali disposti regolarmente su un piano cristallografico con la stessa regolarità presente all’interno del solido, la mancanza di simmetria traslazionale nella direzione perpendicolare alla s. introduce delle modificazioni della struttura elettronica che si rivelano particolarmente importanti, specie nel caso dei semiconduttori. La situazione che caratterizza la struttura elettronica per un solido limitato, ossia in presenza di una s., è illustrata nel semplice caso di un solido unidimensionale in fig. 1. Nella fig. 1A è rappresentata schematicamente l’energia potenziale V(z) di un elettrone, avendo supposto la presenza di una s. a z=0; Evac è l’energia potenziale dell’elettrone fuori dal solido, mentre E è la sua energia totale (cinetica più potenziale). Essendo E minore di Evac, l’elettrone è confinato all’interno del solido. In fig. 1B è riportato il grafico della funzione d’onda Ψ(z) di un elettrone sottoposto al potenziale rappresentato nella fig. 1A, nel caso in cui il vettore d’onda k (legato alla lunghezza d’onda dalla relazione k=2π/λ) sia immaginario (k=−iμ, con μ reale, >0): si vede che lo stato è localizzato in prossimità della s., con energia corrispondente (proprio perché k è immaginario) alle bande proibite del solido infinito.
La presenza della s. introduce cioè stati permessi all’interno delle bande proibite e pertanto modifica drasticamente le proprietà dei solidi, specie degli isolanti e dei semiconduttori. Tali stati, che dal punto di vista chimico sono associati ai legami non saturati degli atomi di s., possono catturare o cedere elettroni, causando la formazione di una carica sulla s. stessa, che a sua volta determina un campo elettrico macroscopico schermato verso l’interno dagli altri elettroni del solido. Si ha cioè un incurvamento delle bande di energia degli elettroni superficiali, che modifica il valore del lavoro di estrazione e il trasferimento di carica tra il solido e le molecole dell’ambiente esterno. Nel caso di un solido reale (tridimensionale) le cose sono più complicate, anche perché intervengono vari altri fattori. A causa dell’energia associata al moto dell’elettrone nel piano superficiale, gli stati di s. possono avere energie non necessariamente corrispondenti a quelle delle bande proibite.
L’esposizione all’ambiente esterno e la presenza di legami insaturi fa sì che la composizione chimica di una s. sia generalmente assai diversa da quella dell’interno del solido; si possono ottenere s. pulite, ossia prive di impurezze chimiche, per es., trattandole fisicamente in vuoto ultra spinto (dell’ordine di 10−13 bar). La disposizione degli atomi di s. è spesso diversa da quella dell’interno del solido sia per quanto riguarda le distanze interatomiche (rilassamento superficiale) sia per quanto riguarda la regolarità (ricostruzione superficiale). La struttura dei difetti di una s. dipende in genere dal modo in cui essa viene creata e dall’energia disponibile in tale processo: la s. tende a esporre, per quanto possibile, i piani di grande impacchettamento cui è associata una minore energia per unità di area. Quando il contatto non avviene tra un solido e un fluido, ma tra due solidi, si parla di interfaccia solida, una struttura che presenta solo alcune affinità con quella delle s. libere. La diversità dei parametri reticolari e delle strutture elettroniche dei due solidi, la carica spaziale della regione dell’interfaccia, l’interdiffusione dei componenti ecc. giocano in questo caso un ruolo essenziale. Lo studio di queste interfacce riveste grande importanza per la tecnologia dei dispositivi a semiconduttore.
La molteplicità e la versatilità delle tecniche sperimentali hanno permesso negli ultimi decenni del 20° sec. uno sviluppo rigoglioso dell’attività di ricerca nel campo della fisica delle superfici. Lo scopo principale di questi studi è quello di ricavare dei modelli per la struttura atomica, elettronica e vibrazionale di una data s. e di utilizzarli per la risoluzione di molteplici problemi, anche tecnologici.
Chimica delle superfici
Gli atomi (o ioni) presenti sulla s. di un solido sono in uno stato diverso da quelli esistenti all’interno, dato che solo una parte delle loro valenze è saturata da atomi (o ioni) vicini. Lo stato d’insaturazione genera negli atomi superficiali caratteristiche strutturali e di reattività tali da determinare comportamenti chimici particolari. Si è così sviluppata una branca della chimica, chiamata appunto chimica delle s., che tratta essenzialmente gli aspetti strutturali e di reattività delle s. dei solidi. La chimica delle s. non prende in esame solo lo strato di atomi appartenenti all’ultimo piano che delimita il solido, in quanto la presenza di una s. modifica la struttura elettronica e quindi le proprietà anche degli atomi appartenenti a strati sottostanti. È da notare che vanno prese in esame anche le s. ‘interne’ dei solidi se accessibili alle specie reagenti, quali quelle esistenti nei pori, nonché quelle esistenti in cavità presenti in alcune strutture, per es., nelle zeoliti (➔).
L’esistenza sulle s. di atomi (o ioni) insaturi porta alla interazione attrattiva verso molecole, ioni e atomi ‘esterni’. Così, nel caso di un gas, questa interazione porta a legare le molecole che vengono a contatto con la s. e si osserva, di conseguenza, un arricchimento della concentrazione delle molecole della specie gassosa sulla s. del solido. Questo fenomeno, denominato adsorbimento, può dar luogo, se la molecola è reattiva e la temperatura sufficiente, a una modificazione profonda della struttura elettronica della molecola adsorbita che determina l’instaurarsi di un vero legame chimico (adsorbimento chimico o chemiadsorbimento), caratterizzato da energia dell’ordine di quelle in gioco nelle reazioni chimiche e dalla formazione di ‘composti superficiali’.
La chimica delle s. ha un ruolo importante in molti processi: corrosione, elettrochimica degli elettrodi, lubrificazione, adesione di strati protettivi, catalisi eterogenea (dove una comprensione a livello atomico delle reazioni di s., che tenga conto anche dell’orientamento molecolare e del punto di impatto sul reticolo, consente il progetto ottimale dei catalizzatori). È da notare che molti processi che coinvolgono l’interno di un solido hanno inizio sulla s., cosicché la chimica delle s. consente di comprendere numerosi fenomeni osservati e studiati nell’ambito di tutta la scienza dei materiali.
Metodiche sperimentali
Le principali metodiche impiegate nello studio delle s. possono essere classificate sulla base del tipo di sonda usata, ossia a seconda che vengano inviati contro la s. fasci di elettroni, di fotoni, di molecole, di ioni ecc. Queste particelle scambiano con la s. energia e impulso e possono estrarne atomi e ioni: le modalità con le quali hanno luogo questi processi forniscono informazioni sulla struttura della superficie. A seconda che venga o meno scambiata energia con la s., le tecniche si classificano inoltre in spettroscopiche o diffrattive. Le tecniche topografiche, infine, sono quelle che forniscono un’immagine della superficie. Ciascuna tecnica mette in luce particolari aspetti della struttura superficiale e ha una sensibilità più o meno elevata nei confronti delle proprietà di superficie. In linea del tutto generale, le tecniche che fanno uso di elettroni o di ioni di bassa energia o di fasci molecolari sono quelle che presentano la massima sensibilità alle proprietà superficiali, data la elevata probabilità che queste particelle hanno di interagire con gli atomi della superficie.
Diffrazione di elettroni lenti. Un elettrone libero con quantità di moto p si comporta alla stregua di un’onda con lunghezza d’onda λ=h/p, dove h è la costante di Planck. Per un elettrone di 100 eV, la lunghezza d’onda è di circa 1,2 Å, ossia dello stesso ordine delle distanze interatomiche. Un fascio di elettroni di tale energia, riflesso da una s. cristallina, subisce fenomeni di diffrazione, rivelabili raccogliendo gli elettroni diffratti su uno schermo fluorescente o mediante opportuni elettrodi. L’analisi delle figure di diffrazione ottenute con questa tecnica, generalmente indicata con la sigla LEED (low energy electron diffraction), fornisce informazioni sulla disposizione degli atomi superficiali, anche se non è sufficiente a definire univocamente un modello di ricostruzione della superficie. Informazioni più dettagliate si ottengono con il metodo della LEED dinamica, in cui viene fatta variare la lunghezza d’onda degli elettroni (variando il potenziale acceleratore). La diffrazione di elettroni lenti è anche sensibile ai difetti microscopici della superficie.
Tecniche spettroscopiche. In esse la particella sonda scambia energia con il sistema, eccitandone i livelli elettronici o vibrazionali. Tali tecniche possono essere suddivise in: spettroscopia ottica di s., spettroscopie elettroniche, spettroscopia di fotoemissione (➔ spettroscopia).
Diffusione superficiale di molecole e ioni. Molecole (o atomi) e ioni vengono spesso utilizzati come sonde per studiare la struttura delle s.; sono possibili sia processi elastici di diffrazione, sia processi anelastici, in cui si analizza lo spettro di velocità delle particelle diffuse o l’emissione di raggi X e di elettroni, per effetto Auger (➔ Auger, Pierre-Victor), nei processi di neutralizzazione superficiale degli ioni. È possibile inoltre analizzare mediante la spettrometria di massa gli ioni secondari emessi per urto o deadsorbiti per effetto termico.
Microscopia. L’osservazione al microscopio (ottico o elettronico) di una s. permette una valutazione globale e quindi l’evidenziazione di difetti su larga scala, di contorni di grani ecc. Nel microscopio elettronico a scansione è possibile analizzare, oltre al fascetto di elettroni che proviene da una specifica piccolissima regione del campione, anche altri segnali (elettroni secondari, elettroni Auger, fotoni, raggi X) prodotti dall’interazione del fascio elettronico con il campione, che possono fornire informazioni sulla composizione chimica della superficie. Dal punto di vista della struttura atomica della s., sono particolarmente utili i microscopi a scansione a effetto tunnel, i microscopi a forza atomica e quelli a emissione di campo (➔ microscopio) che consentono di ottenere una mappa della s. nella quale si distinguono i singoli atomi.
Geologia
In geomorfologia, s. di spianamento, s. pianeggiante che si produce a seguito dell’erosione dei rilievi e che tronca sia le strutture tettoniche sia i diversi tipi di rocce che le compongono; la sua formazione richiede un lungo lasso di tempo geologico; s. strutturale, s. che coincide con la parte superiore di uno strato più resistente, il quale viene evidenziato a seguito dell’eliminazione, per erosione, dei terreni più teneri che lo ricoprivano.
Matematica
In geometria analitica, la figura rappresentata da una equazione in tre variabili del tipo z=f(x, y) oppure, più in generale, f(x, y, z)=0; la s. è parametrica, se le coordinate dei punti dipendono dai valori assegnati a 2 parametri u, v: x=x(u, v), y=y(u, v), z=z(u, v), dove le 3 funzioni x(u, v), y(u, v), z(u, v), definite tutte in un dominio D del piano (u, v), si suppongono per lo più differenziabili e realizzano una corrispondenza biunivoca tra i punti della s. e i punti del dominio D. A questa distinzione si sovrappone una classificazione derivante da altre proprietà (s. algebriche, trascendenti, spaziali, iperspaziali ecc.); alcune s. sono indicate mediante il nome di chi le considerò (per es., s. di Veronese), oppure mediante un nome che indichi una loro proprietà o il modo di generarle (s. di rotazione, s. rigate ecc.).
Proprietà di una superficie
Proprietà algebriche. Per una s. algebrica, si possono considerare alcuni caratteri algebrici: a) l’ordine della s. è il numero dei punti d’incontro della s. con una retta generica dello spazio, tale numero è uguale al grado del polinomio f (x, y, z); b) la classe è il numero dei piani tangenti che si possono condurre alla s. da una retta generica dello spazio; c) il punto s-plo è un punto appartenente alla superficie tale che, detta x la retta generica passante per il punto, tutte le s-intersezioni della retta x sono coincidenti con quel punto; d) la curva s-pla è una curva di punti s-pli per la superficie.
Proprietà differenziali. Si chiama retta tangente alla s. in un suo punto P0 di coordinate x0=x (u0, v0), y0=y (u0, v0), z0=z (u0, v0) ogni retta tangente a qualche linea tracciata sulla s. e passante per P0; in un punto esistono ∞1 rette tangenti, che formano il cono tangente; nei punti ordinari tale cono si riduce a un piano, detto piano tangente, la cui equazione è:
ovvero fx(x0,y0,z0) (x−x0)+fy(x0,y0,z0) (y−y0)+fz(x0,y0,z0) (z−z0)=0 quando l’equazione della s. è data nella forma f(x, y, z)=0. L’intersezione tra il piano tangente e la s. è una curva che ha nel punto di tangenza un punto doppio. Due s. sono dette tangenti in un punto se in esso hanno il medesimo piano tangente. Tangenti asintotiche alla s. in un suo punto semplice P, sono le tangenti a contatto (almeno) tripunto con la s.; in generale ne esistono due distinte (altrimenti tutte le tangenti sono a contatto tripunto, e l’intorno del secondo ordine del punto si dice calotta inflessionale); a seconda che esse siano reali e distinte o reali e coincidenti o complesse coniugate, il punto P si dice rispettivamente iperbolico, parabolico, ellittico. Tangenti coniugate a una s. in un suo punto, sono due tangenti che si corrispondono nell’involuzione che ha per elementi uniti le due tangenti asintotiche. Tangenti di curvatura (o tangenti principali) in un punto sono le tangenti, tra loro perpendicolari, che, insieme con la normale alla s., individuano le due sezioni piane (sezioni normali principali) aventi, tra le sezioni normali in quel punto, curvatura massima e minima rispettivamente.
Normale a una s. in un suo punto è la normale in quel punto al relativo piano tangente. Curvatura media in un punto è la somma delle curvature delle sezioni normali principali (curvature principali); curvatura totale (o curvatura gaussiana) è invece il loro prodotto. Punto singolare o multiplo per la s. è un punto nel quale il piano tangente è indeterminato.
Prima forma quadratica fondamentale: ds2= E du2+2F du dv+G dv2, con E, F, G funzioni opportune di u, v, la quale dà il quadrato della distanza di due punti infinitamente vicini e individua la metrica della superficie. Seconda forma quadratica fondamentale: L du2+2M du dv+N dv2 (con L, M, N funzioni opportune di u, v) rappresenta, a meno di un fattore numerico, la distanza di un punto infinitamente vicino al punto u, v dal piano tangente alla s. in u, v. La conoscenza delle due forme anzidette determina la s. a meno di un movimento.
Tipologie di superficie
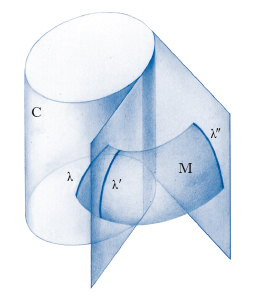
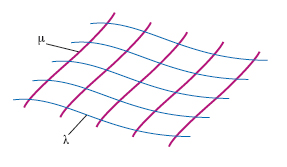
S. algebrica S. rappresentata da un polinomio in tre variabili. S. analitica S. rappresentata da una funzione analitica di 3 variabili. S. applicabili Due s. che, immaginate realizzate con una lamina flessibile e inestensibile, si possono portare a coincidere; più precisamente due s. si dicono applicabili quando hanno la stessa metrica, cioè la stessa prima forma quadratica fondamentale. S. differenziabile S. rappresentata mediante funzioni differenziabili; è lo stesso che varietà differenziabile di dimensione 2 (➔ varietà). S. luogo S. intesa come luogo dei suoi ∞2 punti; si contrappone a s. inviluppo, s. intesa come insieme dei suoi ∞2 piani tangenti; se la s. è sviluppabile ammette solo ∞1 piani tangenti, è allora da intendere come duale di una curva sghemba, che ne è lo spigolo di regresso. S. modanata S. che si può pensare generata come segue: si prenda una s. C (fig. 2) cilindrica, e si pensi a una lamina avvolta sul cilindro (e quindi inizialmente coincidente con esso) sulla quale sia tracciata una linea λ. Si svolge la lamina dal cilindro, in modo da farle assumere una configurazione piana; la linea λ assume allora infinite posizioni come λ′, λ″ ecc.; esse descrivono appunto la s. modanata M; ogni punto della λ descrive, in un piano ortogonale alle generatrici del cilindro, un’evolvente (➔ evoluta) del cerchio che è sezione del cilindro con quel piano. Come caso limite, quando il cilindro si riduca a una retta, la s. modanata diventa una superficie di rotazione. S. parallela a una s. data S. luogo degli estremi dei segmenti di lunghezza costante l riportati sopra le normali alla s. data, e aventi un estremo sulla s. stessa. Essa è anche inviluppo delle sfere di raggio l aventi il centro sulla s. data. S. razionale S. algebrica per la quale esista una corrispondenza birazionale tra i suoi punti e i punti di un piano. Sono s. razionali tutti i monoidi, cioè le s. d’ordine n con un punto (n−1)-plo. S. riducibile (o s. spezzata) S. algebrica somma di due parti (proprie) ciascuna delle quali sia a sua volta una s. algebrica. Sono riducibili quelle s. la cui equazione si ottiene uguagliando a zero il prodotto di due polinomi, cioè quelle per le quali f(x, y, z) è un polinomio riducibile. Una s. non riducibile, dall’equazione non fattorizzabile, si dice irriducibile. S. rigata S. costituita da infinite rette (➔ rigata). S. sviluppabile S. applicabile sopra un piano; è necessariamente rigata e ha soltanto ∞1 piani tangenti anziché ∞2. S. di traslazione S. generata dal moto rigido traslatorio di una linea λ, un punto prefissato della quale descrive una certa linea μ. Essa si può ottenere anche muovendo μ in modo che un suo punto descriva λ (fig. 3).
Tecnica
In meccanica, s. di lavorazione, le s. dei pezzi così come ottenute in uscita dalla fonderia dopo lavorazioni plastiche, alle macchine utensili ecc. Queste s., a causa delle lavorazioni stesse, si scostano, in modo più o meno sensibile, dalle s. geometriche ideali risultanti dal disegno dei pezzi stessi. Le irregolarità superficiali si identificano con i solchi dell’utensile o dell’abrasivo, con le impronte dei granuli di sabbia derivanti dalla formatura, oppure corrispondono alle irregolarità superficiali dello stampo, delle trafile, dei cilindri del laminatoio. Tra le irregolarità, ve ne sono di piccola ampiezza (rugosità o scabrosità), dovute agli spigoli taglienti degli utensili e dei granuli abrasivi e ve ne sono altre a carattere periodico (ondulazioni), dovute a difetti di guida del pezzo o dell’utensile, a vibrazioni delle macchine operatrici, a irregolarità nell’alimentazione, all’eccentricità di parti rotanti ecc. Alle caratteristiche superficiali si ricollegano le proprietà fisiche e tecnologiche di un materiale, o di un pezzo, come la durezza, la resistenza all’usura, alla corrosione, alle sollecitazioni di fatica, il potere adsorbente, il potere polarizzante, cioè quello di orientare o polarizzare le molecole dei corpi adsorbiti o aderenti.