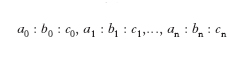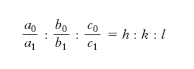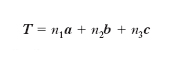cristallo

Chimica

Porzione di materia allo stato solido, chimicamente e fisicamente omogenea, che ha forma poliedrica ( stato cristallino). In essa le molecole, gli atomi o gli ioni sono disposti in modo regolare secondo una struttura tridimensionale caratteristica del materiale. Le proprietà delle sostanze cristalline dipendono dalla loro particolare struttura intima e non dalla forma poliedrica che esse assumono. Per i c. si usano attributi diversi secondo che si voglia indicarne l’abito, che è dato dalle dimensioni e dal tipo della forma predominante (c. aciculari, prismatici, colonnari, tubolari, bipiramidati ecc.) o una loro particolare composizione chimica.

Leggi della cristallografia morfologica

La forma poliedrica dei c. è conseguenza della loro velocità d’accrescimento che si manifesta come proprietà anisotropa discontinua, cioè con valori diversi nelle varie direzioni. In condizioni di libertà d’accrescimento le facce hanno uguale distanza dal centro del c. e quindi uguale contorno geometrico; in questo caso, all’equivalenza fisica corrisponde un’equivalenza di figura e di dimensioni delle facce e il solido viene detto c. modello. Libertà d’accrescimento si verifica quando un c. è a contatto con una massa fluida avente una concentrazione omogenea da cui trae alimento per l’intero periodo di formazione. Queste condizioni si realizzano difficilmente in natura: è sufficiente che una faccia sporga dal livello della soluzione o che poggi sul fondo dell’ambiente che la contiene, perché su di essa cessi ogni ulteriore deposito di particelle. A causa di tali perturbazioni, indipendenti dalle proprietà del c., le facce di una stessa forma finiscono per avere contorno e dimensioni diverse perché quelle più alimentate, spostandosi parallelamente a sé stesse, si allontaneranno dal centro del germe più delle altre; i solidi naturali, nei quali facce fisicamente equivalenti non hanno uguale forma e dimensioni, sono detti sproporzionati. Dato che la sproporzione è conseguenza di un maggiore o minore spostamento parallelo delle facce, gli angoli diedri di un c. sproporzionato sono uguali a quelli del corrispondente cristallo modello: è questa la legge della costanza dell’angolo diedro, la prima della cristallografia, formulata da N. Stenone nel 1665.

Tenuto conto di questa legge e dei turbamenti di sviluppo, in cristallografia la nomenclatura delle forme non può adattarsi del tutto ai criteri della geometria. In geometria una forma semplice è definita dall’equivalenza geometrica delle facce e dagli angoli che esse formano fra loro mentre in cristallografia è definita dall’equivalenza fisica delle facce e dagli angoli che esse formano fra loro. In geometria, per es., un cubo è limitato da 6 facce uguali a contorno quadrato ortogonali fra loro, in cristallografia è limitato da 6 facce fisicamente equivalenti ortogonali fra loro: perciò un cubo di salgemma sarà sempre definito con questo nome anche se, a causa della sproporzione, si trovi ad assumere la forma di un prisma a base rettangolare o quadrata.

Per individuare la posizione delle facce di un c. può convenire riferirle a un sistema trirettangolo di assi cartesiani OXYZ, con l’origine O in un punto interno al c. e gli assi Z e X orientati, il primo secondo la verticale ascendente, il secondo verso l’osservatore. Una superficie piana resta allora perfettamente definita nella sua posizione assoluta (inclinazione rispetto agli assi e distanza dal centro) quando si conoscono i parametri, cioè i segmenti OA, OB, OC che essa taglia o verrebbe a tagliare sugli assi coordinati se opportunamente sviluppata; la stessa superficie resta invece individuata soltanto nella giacitura (inclinazione rispetto agli assi) se si conoscono i rapporti parametrici OA: OB: OC. Dato che nei c. ciò che interessa è la giacitura delle facce e non la loro posizione assoluta, le facce stesse vengono abitualmente rappresentate mediante i rapporti parametrici. Se si considerano i rapporti parametrici

di tutte le possibili facce dei c. di una data sostanza e se a uno qualsiasi di essi, per es. a₀ : b₀ : c₀, spettante a una faccia F che incontra tutti e tre gli assi, si riferisce il rapporto di una qualsiasi delle rimanenti, per es. a₁ : b₁ : c₁ spettante a una faccia che potremo chiamare M, si ha che:

,

dove h, k, l, detti indici della faccia M, sono numeri razionali, riducibili sempre a numeri interi di solito semplici, cioè costituiti di una sola cifra, lo zero compreso. È questa la seconda legge della cristallografia morfologica che va anche sotto il nome di legge della razionalità degli indici (o legge degli indici semplici o legge di Haüy). Il rapporto a₀ : b₀ : c₀ che serve di riferimento per tutti gli altri è denominato rapporto parametrico fondamentale.

Strutture e reticoli cristallini

I materiali solidi che risultano privi di struttura regolare sono chiamati amorfi. Mentre nei gas e nei liquidi le molecole e gli atomi, pur interagendo tra loro, hanno una notevole libertà di muoversi gli uni rispetto agli altri, nei c. e nei solidi in genere tale libertà è fortemente limitata. La distinzione tra fase solida e fase liquida in termini di assetto periodico degli atomi e delle molecole è meno netta di quanto possa sembrare a prima vista. In alcuni liquidi organici, per es., le molecole si dispongono in modo regolare in almeno una direzione (come nei c. liquidi); d’altra parte i solidi amorfi possono essere considerati sotto molti aspetti come liquidi ad alta viscosità. Una sostanza policristallina è costituita da numerosi piccoli c., orientati diversamente l’uno rispetto all’altro, ma tutti aventi al loro interno una distribuzione ordinata degli atomi. Poiché nei c. reali esiste un numero elevato di possibili disposizioni ordinate degli atomi e delle molecole, un primo passo nel loro studio è quello di classificarli in modo organico. La soluzione di tale problema, proprio della cristallografia, è in realtà di utilità generale per le implicazioni che le diverse strutture cristalline hanno sulle proprietà fisiche dei materiali.

1A

2

Le strutture più semplici presentate dai c. sono quelle ‘compatte’: esse sono prevedibili per c. costituiti da un solo tipo di atomi, che comportandosi come piccole sfere attraggono le sfere vicine in tutte le direzioni. Ogni atomo tende ad attrarre a sé, il più vicino possibile, il maggior numero di atomi. Riferiamoci, allora, al semplice ma efficace modello in cui gli atomi sono rappresentati da sfere rigide tra loro tangenti, opportunamente accatastate su piani successivi in modo da formare il solido. Fig. 1A mostra uno strato di tali sfere. Lo strato immediatamente superiore può essere ottenuto disponendo le sfere in due possibili modi: o esattamente sopra gli atomi del primo piano, disposizione che chiameremo A e corrisponde alla struttura esagonale semplice (ogni sfera è circondata da altre sei sfere disposte sui vertici di un esagono), oppure negli avvallamenti (fig. 1B), disposizione che chiameremo B. Diciamo che nei due casi la struttura, passando dal primo al secondo strato, è caratterizzata da una sequenza AA e AB rispettivamente. Un terzo strato di atomi può essere sistemato ancora in due modi diversi: o negli avvallamenti situati direttamente sopra le sfere del primo piano (sequenza di strati del tipo ABAB ...) o nei rimanenti avvallamenti (fig. 1C), disposizione che chiameremo C, in quest’ultimo caso avremo una sequenza di strati del tipo ABCABC ... L’assetto ABAB ... è detto struttura esagonale compatta. L’assetto ABCABC ... conduce a una struttura cubica; poiché per ogni faccia del cubo esiste una sfera nel centro, tale struttura è detta struttura cubica a facce centrate (fig. 2). Queste strutture sono le più dense e sono proprie di molti metalli. In taluni casi la forte somiglianza delle due strutture fa sì che un solido possa presentare l’una o l’altra di esse a seconda della temperatura, con una precisa temperatura di transizione tra le due fasi.

Anche se le strutture compatte sembrano le più naturali per un ‘impacchettamento’ degli atomi, tuttavia esiste una grande varietà di c. che hanno forme diverse e disposizioni atomiche molto più complesse di quelle fino qui riportate. Allo scopo di individuare tutte le possibili forme cristalline proviamo a pensare un c., dal punto di vista geometrico, come l’insieme di punti ( reticolo) legati tra loro dall’operazione di traslazione T definita dalla seguente espressione:

,

dove n₁, n₂, n₃ sono numeri interi e a, b, c sono detti vettori fondamentali di traslazione. Ogni punto del reticolo può essere raggiunto con un’unica operazione di traslazione T tramite un’opportuna scelta degli interi n₁, n₂, n₃. Il reticolo ha solo significato geometrico e per costruire un c. occorre associare atomi, ioni o molecole a ogni suo punto. Si definisce base il gruppo di atomi associato a ogni punto reticolare. La base può essere costituita da un solo atomo o da più atomi che, a loro volta, possono essere di uno stesso elemento o di elementi diversi. Si definisce cella unitaria qualsiasi cella del reticolo che con operazioni di traslazione genera l’intero cristallo. È detta cella primitiva la cella unitaria individuata dai tre minimi vettori fondamentali di traslazione (vettori primitivi). Essa è perciò la cella unitaria di minimo volume e presenta punti del reticolo solo ai vertici.

3

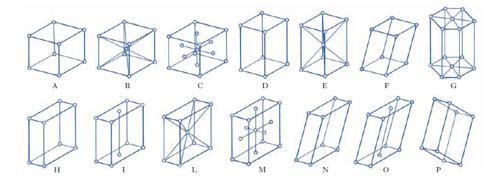
Il concetto di cella unitaria fu proposto per la prima volta da C. Huygens nel 1690 nel Trattato di ottica, per interpretare le proprietà ottiche della calcite. La forma a rombo dei piani di sfaldatura della calcite suggerì ad Huygens che il c. dovesse essere composto di tanti sferoidi appiattiti. Più tardi l’abate R.J. Haüy ipotizzò che un c. di calcite fosse costituito dall’accatastamento di tanti piccoli blocchetti romboedrici (celle unitarie). Questa ipotesi fu poi estesa supponendo che ciascun c. abbia un suo caratteristico edificio cristallino realizzato con celle unitarie di forma diversa, come per es. cubi, prismi quadrati, prismi rettangolari ecc. Spesso si usa la direzione dei vettori di traslazione primitivi per definire gli assi cristallografici. Il volume V_p di una cella primitiva definita dai vettori primitivi di traslazione a, b, c è V_p = ∣ a ⋀ b × c ∣; gli angoli compresi tra a, b, c si indicano generalmente con α, β, γ. Tenendo presente la definizione di reticolo, si dimostra che le possibili combinazioni dei vettori primitivi in tre dimensioni conducono a 14 reticoli irriducibili ( reticoli di Bravais), raggruppabili in sette sistemi (fig. 3):

1) Sistema monometrico, a=b=c, α=β=γ=90°: A) cubo semplice, B) cubo centrato, C) cubo a facce centrate.

2) Sistema tetragonale, a=b≠c, α=β=γ 90°: D) prisma retto a base quadrata semplice, E) prisma retto a base quadrata centrato.

3) Sistema trigonale o romboedrico, a=b≠c, α=β=90°, γ≠90°: F) romboedro semplice.

4) Sistema esagonale, a = b≠c, α=β=90°; γ=120°: G) prisma a base esagonale.

5) Sistema rombico, a≠b≠c, α=β=γ=90°: H) prisma retto a base rettangolare semplice, I) prisma retto a base rettangolare centrata, L) prisma retto a base rettangolare, centrato, M) prisma retto a base rettangolare, a facce centrate.

6) Sistema monoclino, a≠b≠c, α=γ=90°≠β: N) prisma obliquo a base rettangolare semplice, O) prisma obliquo a base rettangolare centrata.

7) Sistema triclino, a≠b≠c, α≠β≠γ≠90°: P) prisma obliquangolo semplice.

Simmetrie cristalline

La classificazione delle strutture cristalline fatta da A. Bravais si basa sulla sola proprietà di traslazione dei reticoli. Una classificazione più completa può essere fatta in termini delle proprietà di simmetria che le strutture cristalline mostrano intorno a un punto reticolare; infatti, oltre alla traslazione, esistono altre operazioni di simmetria che lasciano il reticolo invariato.

Rotazione Se un reticolo, dopo essere ruotato di un angolo pari a 360°/n intorno a un asse, torna in sé stesso, allora si dice che possiede un asse di simmetria di rotazione di molteplicità n; n può solo avere i valori 2 (asse binario), 3 (ternario), 4 (quaternario) o 6 (senario).

Riflessione Rispetto a un piano: i piani di riflessione sono piani immaginari che attraversano il reticolo in modo tale che una metà sia l’immagine esattamente speculare dell’altra.  Inversione Operazione di simmetria che permette di ottenere lo stesso reticolo sostituendo a ogni punto reticolare descritto dal raggio vettore r il punto − r. Se un cristallo ha tutti gli atomi a coppia disposti in − r e r, intorno a un punto origine opportuno, si dice che possiede un centro di simmetria.

I c. che hanno gli stessi elementi di simmetria appartengono tutti alla stessa classe cristallina. Si dimostra che dalle possibili combinazioni delle operazioni di simmetria (rotazione, riflessione, inversione) si ottengono 32 classi cristalline che più propriamente sono anche dette gruppi puntuali. Per un c. reale, si può immaginare dunque una operazione di simmetria più complessa ottenuta con operazione di rotazione o di riflessione seguita da un’altra di traslazione; tale operazione può essere considerata come il prodotto di due operazioni, e tale da lasciare quindi il c. invariato. Un insieme di tali operazioni viene detto gruppo spaziale. Si dimostra che esistono 230 gruppi spaziali possibili che corrispondono ad altrettanti modi diversi in cui atomi e molecole possono disporsi per formare delle strutture cristalline.

Alcune proprietà fisiche che caratterizzano i c. sono una diretta conseguenza della loro simmetria. Per es., in un c. cubico, comunque applichiamo il vettore campo elettrico E, si ha un vettore densità di corrente J che ha la stessa direzione e verso di E, cioè sussiste la relazione J = σ E, dove σ è una costante, chiamata conducibilità. Si dice anche che la conducibilità è isotropa. Che ciò sia vero si intuisce dal fatto che l’assetto cristallino è indistinguibile lungo uno spigolo del cubo da quello che si osserva lungo un altro spigolo; pertanto la resistenza elettrica e quindi la conducibilità devono essere le stesse lungo i tre assi principali della struttura cubica. Se il campo elettrico E è in una direzione qualsiasi, con proiezioni E_x, E_p, E_z rispetto agli assi principali del cubo, sarà anche J_x = σ E_x, J_y = σ E_y, J_z = σ E_z, per cui J = σ E. Un altro fenomeno direttamente legato alla struttura cristallina è quello ottico della birifrangenza: è noto che molti c., quali, per es., la calcite, hanno in generale la proprietà di dividere in due un fascio di luce non polarizzata che incida su di essi.

Un modo semplice, derivato dal metodo del rapporto parametrico, per individuare piani e direzioni reticolari è di indicarli con gli indici di Miller. Si consideri, per es., un piano qualunque nel c. e le sue intersezioni con assi coordinati che avremo assunto coincidenti con gli assi stessi del c., vale a dire i vettori a, b, c, della cella primitiva. Misurate le intersezioni lungo gli assi in unità a, b, c, se ne prendono i reciproci e si calcolano i più piccoli numeri interi che stanno tra loro negli stessi rapporti. Questi tre numeri sono gli indici di Miller del piano e si indicano tra parentesi tonde (h, k, l). Con la stessa notazione si indica anche una famiglia di piani paralleli ed equidistanti. Se un piano taglia un asse nella parte negativa rispetto all’origine il corrispondente indice di Miller sarà negativo e viene indicato con una linea sopra l’indice. Gli indici di Miller individuano nei reticoli cubici anche la direzione normale al piano che essi rappresentano; in tal caso essi sono i minimi interi che stanno tra loro come i coseni direttori della normale al piano e vengono generalmente scritti tra parentesi quadre [h, k, l]. È chiaro che piani (o rette) tra loro paralleli sono caratterizzati dagli stessi indici di Miller.

Legami cristallini

Una diversa classificazione dei c. può essere fatta, anziché in termini della loro struttura, in base al tipo di legame tra gli atomi che li caratterizza. I tipi fondamentali di legame sono: il legame ionico, il legame covalente, il legame metallico e il legame molecolare. Questa schematizzazione è però solo indicativa in quanto frequentemente i c. presentano caratteristiche intermedie e solo in alcuni casi si può dire che un c. presenta in modo evidente un determinato tipo di legame. In ogni caso la coesione nei solidi è essenzialmente determinata dalla interazione elettrostatica attrattiva tra le cariche negative degli elettroni e le cariche positive dei nuclei. In ogni solido l’energia potenziale è determinata da un termine negativo rappresentante le forze attrattive e uno positivo rappresentante le forze repulsive.

4

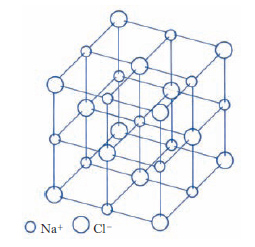
Nei c. ionici gli elettroni sono trasferiti da atomi elettropositivi ad atomi elettronegativi e il legame è determinato dall’interazione elettrostatica coulombiana degli ioni così formati. Naturalmente ciascuno ione tende a circondarsi di ioni di carica opposta, mentre ioni dello stesso segno occupano posizioni reticolari più distanti. Un tipico esempio è il cloruro di sodio (fig. 4). Una stima dell’energia di attrazione coulombiana permette di verificare che, in tutti i composti fortemente ionici, l’interazione elettrostatica è la principale responsabile della coesione. Il grado di ionizzazione degli atomi costituenti un c. ionico è spesso tale che le configurazioni elettroniche di tutti gli ioni corrispondono a strati elettronici completi, proprio come nei gas inerti. In modo analogo al caso dei gas inerti ci si può quindi aspettare che la distribuzione elettronica intorno a ciascuno ione abbia approssimativamente una simmetria sferica, eccettuata qualche distorsione nella regione di contatto di due atomi vicini. È evidente che dal punto di vista elettrico i c. ionici si comportano come degli isolanti ed eventuali fenomeni di conducibilità elettrica sono dovuti al moto di ioni o vacanze nel cristallo, anziché al moto di elettroni. Nei c. ionici, dato che le forze coulombiane non sono direzionali, le dimensioni degli ioni sono determinanti ai fini della struttura finale. L’energia di coesione dei c. ionici può essere calcolata come somma dell’energia di interazione estesa a tutte le coppie di ioni e può essere determinata sperimentalmente da dati termochimici per mezzo del ciclo di Born-Haber.

5

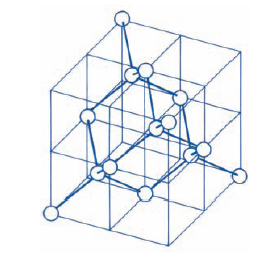
In molti c., il legame (covalente eteropolare o omopolare) tra gli atomi risulta invece dal fatto che uno o più elettroni forniti dagli atomi che partecipano al legame sono condivisi tra gli atomi stessi. In un legame covalente gli elettroni condivisi servono generalmente per completare lo strato esterno di ciascun atomo. Nel diamante, esempio tipico dei solidi con atomi a valenza quattro, ciascun atomo di carbonio è circondato da quattro atomi uguali posti ai vertici di un tetraedro (fig. 5) e con essi condivide i suoi quattro elettroni di valenza.

Un notevole numero di c. presenta caratteristiche intermedie tra il legame ionico e quello covalente. Tipici esempi sono i semiconduttori composti III-V (cioè formati da elementi appartenenti al III e V gruppo del sistema periodico), come il GaAs, e II-VI, come lo ZnS. Diversamente dai casi precedenti i metalli si devono pensare come un insieme di ioni positivi immersi in una più o meno uniforme nube costituita dagli elettroni di valenza. Il legame metallico è caratterizzato dall’interazione elettrostatica attrattiva fra elettroni e ioni e quella repulsiva delle cariche dello stesso segno. L’alta conducibilità elettrica è dovuta al fatto che nel tipo di legame discusso gli elettroni di valenza non sono legati a nessun atomo in particolare.

I c. molecolari sono infine caratterizzati da deboli forze di legame (legame idrogeno, forze di Van der Waals) causate dall’interazione dei dipoli elettrici permanenti o istantanei; l’energia di legame in tali solidi è piuttosto piccola: ne è tipico esempio la fase solida dei gas inerti.

Imperfezioni nei cristalli

Finora si è parlato di strutture cristalline ideali, cioè perfette. In realtà i c. presentano imperfezioni che comprendono difetti accidentali, dovuti al fatto che le condizioni di crescita non sono state quelle ideali, e difetti che esistono come risultato delle condizioni di equilibrio termodinamico. Mentre si possono quasi del tutto eliminare i difetti accidentali, mediante raffinamenti delle tecniche di crescita, è impossibile eliminare i difetti che derivano dall’equilibrio termodinamico. I difetti sono costituiti da siti reticolari vacanti, da impurezze o da atomi interstiziali. In quest’ultimo caso gli atomi occupano delle posizioni che in un reticolo perfetto non sarebbero occupate. Queste imperfezioni, come pure le impurezze estranee che entrano in posizione sostituzionale degli atomi del solido o in posizione interstiziale, hanno un marcato effetto sulle proprietà del materiale, sia quelle di trasporto sia quelle ottiche, e influiscono in maniera spesso determinante sul comportamento dei dispositivi a stato solido. Oltre ai difetti puntiformi sopra citati esistono difetti che interessano intere linee di atomi del c.: in questo caso si parla di dislocazioni. Esistono infine altri tipi di difetti complessi, tra cui conviene ricordare i cosiddetti bordi di grano, che sono serie di dislocazioni a spigolo consecutive e interessano interi piani di atomi. Questi difetti costituiscono tipicamente la superficie di separazione tra due monocristalli di diversa orientazione e sono quindi molto numerosi nei materiali policristallini.

Tecnica

Nella tecnica, si intende per c. un prodotto dell’industria vetraria, che si distingue dal vetro ordinario per essere perfettamente trasparente, incolore, lucente, assai dispersivo e particolarmente atto alla molatura e all’incisione. È essenzialmente costituito da miscele di sabbia quarzosa, minio e carbonato potassico (in proporzioni di circa 3:2:1), cui talora si aggiunge acido borico e ossido di zinco, fusi a elevata temperatura; l’elevato modulo di elasticità gli conferisce una sonorità metallica; le sfaccettature ne mettono in risalto la rifrangenza, con bellissimi effetti decorativi. Si hanno vari tipi di c.: tra i più pregiati è il c. di Boemia, c. potassico-calcico, preparato partendo da composti puri; rispetto al c. ordinario, o c. al piombo, è più leggero, più duro, meno fusibile, ha buona sonorità, si usa per oggetti artistici, per servizi da tavola ecc.

Il c. di Boemia fu prodotto inizialmente dalle vetrerie tedesche (Slesia, Sassonia, Baviera) e fu trattato come il c. di rocca, e intagliato, specie a Praga (G. Lehmann, G. Schwanhardt), a imitazione delle opere degli incisori italiani chiamati a corte da Rodolfo II (1576-1612). L’industria raggiunse la massima fioritura nella prima metà del 18° sec., ma presto prevalsero criteri commerciali. La concorrenza dei vetri inglesi, alla metà del 18° sec., indusse ad adottare il colore, già abbandonato da Lehmann: si ebbe così il tipo che fu poi preferito nel 19° secolo. L’industria del c. di Boemia, bianco e colorato, è tuttora fiorente nella Repubblica Ceca; nel 1928 se ne è introdotta la fabbricazione anche in Italia, a Murano.

Il mezzo c. è un prodotto più economico, in cui circa metà della potassa è sostituita dalla soda e gran parte del minio è sostituito da ossidi di calcio, bario e zinco; il colore talora tende leggermente al giallastro. Il mezzo c. di Boemia differisce dal c. di Boemia per il fatto che una parte di ossido potassico è sostituita da ossido di sodio; è più fusibile, e più facilmente lavorabile del c.; si usa quando si richieda una completa assenza di colorazione.

Il cosiddetto c. temprato e il c. di sicurezza sono vetri sottoposti a particolari trattamenti.