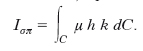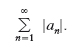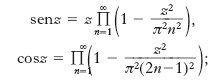prodotto

Tutto ciò che la terra produce o che costituisce il risultato di un’attività umana.

Diritto

La categoria dei p. alimentari, che tende a sostituire quella dei p. agricoli, intesi come frutti naturali, ha assunto rilievo giuridico crescente con lo sviluppo dei mercati e l’esigenza sempre più avvertita di garantire sicurezza ai consumatori. In essa si tendono poi a ricomprendere prodotti miranti a promuovere la salute, oltre che la nutrizione, come nel caso degli integratori alimentari. La disciplina, nella quale svolge un ruolo importante l’Unione Europea, prevede fra l’altro un’autorità per la sicurezza alimentare, con sede in Italia, norme sulla etichettatura volte a consentire il controllo della qualità e della tracciabilità del ciclo di produzione e distribuzione, norme che promuovono qualità relative ai p. tipici. In particolare, per proteggere la tipicità di alcuni p. alimentari l’Unione Europea ha tutelato le produzioni legate al territorio con l’introduzione delle denominazioni di origine e delle indicazioni geografiche (➔ indicazione). La sigla STG (specialità tradizionali garantite) riguarda poi i p. ottenuti secondo un metodo di produzione tipico, tradizionale di una particolare zona geografica, al fine di tutelarne la specificità.

Economia

Risultato di un’attività produttiva, ossia il bene o servizio ottenuto mediante la trasformazione di altri beni o servizi; nel quadro generale dei beni economici i p. possono considerarsi distinti dai beni strumentali e dalle materie prime e in tal caso si identificano con i beni di consumo, ma qualsiasi impresa considera p. il risultato della sua attività e da questo punto di vista sono p. anche i beni strumentali e anche le materie prime, quando sia necessario svolgere un’attività per poterne disporre. Con riferimento a una singola unità di produzione si parla di p. totale (quantità di beni prodotti), di p. medio (rapporto tra il p. totale e il numero delle unità di fattori produttivi impiegati) e di p. marginale (incremento del p. totale in funzione dell’incremento delle unità di fattori produttivi impiegati).

In contabilità nazionale si intende per p. interno lordo (PIL) l’insieme dei beni e servizi prodotti sul territorio nazionale in un determinato periodo di tempo indipendentemente dalla nazionalità dei produttori (esclusi quindi i residenti all’estero) e al lordo degli ammortamenti. Sottraendo al valore del PIL, calcolato sulla base dei prezzi di mercato, il valore delle imposte indirette e sommandovi le sovvenzioni pubbliche alle imprese, si ottiene il PIL al costo dei fattori. Detraendo gli ammortamenti si ottiene invece il p. interno netto. Sommando al valore del PIL il reddito prodotto dai residenti all’estero e sottraendo il reddito prodotto all’interno del paese dai non residenti, si ottiene il p. nazionale lordo (PNL) che, in termini reali, è l’insieme di tutti i beni finiti, diretti e strumentali, prodotti in un anno dalla collettività e, in termini monetari, il valore dei beni stessi ai prezzi di mercato; detraendone i beni o il valore dei beni strumentali prodotti per rimpiazzare quelli logorati nella produzione o obsoleti, cioè le quote d’ammortamento, si ottiene poi il p. nazionale netto.

Dato che questo flusso di produzione crea un analogo flusso di reddito per tutti coloro che partecipano alla produzione, il p. nazionale lordo viene a coincidere con il reddito nazionale lordo o somma di tutti i redditi guadagnati nella produzione dei beni e servizi. Per questa ragione il p. o reddito nazionale lordo si può valutare sia sommando il valore dei beni e servizi prodotti (ai prezzi di mercato) sia sommando il valore dei redditi creati nel corso della produzione di quei beni e servizi (al costo dei fattori di produzione) sia infine sommando i valori aggiunti. Per il calcolo del reddito nazionale lordo e netto ➔ reddito.

Il p. netto (produit net), o sovrappiù, secondo i fisiocrati, era soltanto la differenza tra il reddito dell’agricoltura e delle industrie estrattive e le anticipazioni necessarie per la produzione agricola e mineraria; questi economisti consideravano infatti sterili le altre attività economiche e ritenevano che tutte le classi sociali vivessero sul p. netto della terra e delle miniere, messo in circolazione dai proprietari fondiari acquistando beni o servizi.

Fisica

In fisica dello stato solido, p. np, quello tra il numero di elettroni e il numero di lacune nella banda di conduzione presenti nell’unità di volume di un semiconduttore; per un dato semiconduttore è costante a una data temperatura.

In dinamica e in scienza delle costruzioni intervengono, accanto ai momenti d’inerzia, i cosiddetti p. d’inerzia (detti anche momenti di deviazione); essi d’altronde già compaiono nella legge di variazione del momento d’inerzia con la rotazione della retta cui esso si riferisce (➔ momento). Per un sistema di n masse puntiformi mi concentrate in altrettanti punti Pi, il p. d’inerzia è dato dalla somma degli n termini che si ottengono moltiplicando le singole masse per le loro distanze da due piani prefissati σ e π:

Per un sistema continuo C, detta μ la densità, h e k le distanze da σ e π del generico elemento dC del sistema, il p. d’inerzia vale:

Quando i due piani σ e π coincidono, il p. d’inerzia s’identifica con il momento d’inerzia planare. Per i sistemi contenuti tutti in un piano si considerano i p. d’inerzia rispetto a rette del piano, così come si fa per i momenti d’inerzia; in tal caso si considerano naturalmente le distanze delle varie masse da due rette qualunque del loro piano.

Matematica

Il termine p. si usa in matematica per indicare il risultato di svariati tipi di operazioni che, in qualche modo, si possono però tutte ravvicinare alla moltiplicazione ordinaria. Quasi tutti i tipi di p. godono, per es., della proprietà associativa (l’eccezione più importante è data dal p. vettoriale); buona parte di essi gode della proprietà commutativa (come il p. scalare, il p. topologico, il p. di convoluzione), mentre in alcuni casi il p. è anticommutativo o alternante (ossia invertendo l’ordine dei fattori si muta nel suo opposto, come il p. vettoriale) e in altri (p. di matrici, p. di quaternioni) non è né commutativo né anticommutativo.

La proprietà di annullamento del p. è la proprietà in base alla quale, nel caso di insiemi dotati di un certo tipo di struttura algebrica, il p. risulta nullo soltanto se è nullo uno almeno dei fattori. La proprietà è verificata non solo negli insiemi dei numeri reali o complessi ma, più in generale, in qualsiasi corpo (anche non commutativo, come il corpo dei quaternioni) e anzi in tutti quei tipi di anelli che si chiamano domini di integrità proprio perché, da questo punto di vista, costituiscono una generalizzazione dell’anello dei numeri interi. Soltanto in tali tipi di anelli la relazione ab=ac (con a, b, c non nulli) implica b=c: difatti, in caso non valga il principio di annullamento del p., potrebbe risultare ab=ac=0 anche con b≠c. Si comprende perciò che solo nei domini d’integrità si può operare secondo le abituali regole dell’algebra elementare e, in particolare, eseguire ‘semplificazioni’ come quella indicata.

P. diretto esterno di due gruppi

Considerati due gruppi G, G′ si chiama p. diretto esterno di G, G′ e si indica con G×G′ il gruppo H tale che elementi di H sono le coppie (g, g′), ove g è un elemento di G e g′ di G′; inoltre la legge gruppale di H è definita da (g₁, g′₁) (g₂, g′₂)=(g₁g₂, g′₁g′₂), dove g₁ g₂ e g′₁ g′₂ indicano i p. nei gruppi G e G′ rispettivamente. In modo analogo si definisce il p. diretto esterno di più di due gruppi, come pure di due anelli o due corpi ecc.

P. infinito

Assegnata una successione di numeri reali o complessi a₁, a₂, … a_n, … si chiama p. infinito relativo a tale successione l’espressione

[1] formula

Fattori del p. infinito sono ciascuno dei numeri 1+a₁, 1+a₂ ecc.; si dice che il p. infinito ha valore P≠0 (o converge a P) se il limite lim _n→∞ (1 + a₁)(1 + a₂)…(1 + a_n) esiste e vale appunto P, mentre si dice che è nullo o anche che diverge a zero se tale limite P è uguale a zero. Naturalmente un p. infinito diverge a 0 se uno dei suoi fattori è nullo, o anche se la successione dei fattori è infinitesima; ciò però non è necessario, come è mostrato dall’esempio (1/2)∙(2/3)∙(3/4) …∙(n/n+1) … nel quale la successione dei fattori tende a 1 nonostante che il p. sia nullo. Vari collegamenti esistono tra la teoria dei p. infiniti e la teoria delle serie: per es., si dimostra che il p. infinito [1] converge se e solamente se converge la serie

[2] formula

oltre che tanto il p. [1] quanto la serie [2] convergono commutativamente ossia indipendentemente dall’ordine dei fattori del p. (o, rispettivamente, dei termini della serie) se converge la serie

[3] formula

La locuzione «il prodotto [1] diverge a 0» in apparenza paradossale si spiega appunto perché in questo caso la serie [2] diverge a −∞. Uno dei più celebri p. infiniti è dato dalla formula di J. Wallis:

Si considerano spesso p. infiniti nei quali i fattori non sono numeri bensì funzioni di una o più variabili reali o anche complesse definite in un opportuno insieme E; si danno allora, analogamente al caso delle serie di funzioni, le nozioni di convergenza uniforme e di convergenza totale in relazione a un sottoinsieme E′ di E. Sono classiche le relazioni:

esse sono valide per ogni valore complesso della z, e la convergenza è inoltre uniforme in ogni insieme limitato del piano complesso. Dalla prima di esse, posto z=π/2, si riottiene la formula di Wallis. Anche la funzione gamma di Eulero ha un’interessante rappresentazione come p. infinito, e cioè:

Per il p. esterno (lo stesso che p. vettoriale), per il p. interno (lo stesso che p. scalare) e per il p. misto ➔ vettore.

Per il p. di matrici ➔ matrice.

P. di due sottoinsiemi di un gruppo

Se A, B sono due qualunque sottoinsiemi di un insieme G dotato di una struttura di gruppo (o anche di struttura algebrica di altro tipo) si chiama p., di A, B e si indica con AB l’insieme degli elementi di G che si ottengono componendo, secondo la legge gruppale, due qualsiasi elementi a di A e b di B rispettivamente.

Per il p. tensoriale (o anche p. tensore) di due o più spazi vettoriali ➔ spazio.

P. topologico di spazi topologici

Se X, Y sono due spazi topologici, all’insieme p. cartesiano X×Y si può attribuire in modo spontaneo una topologia, operando nel seguente modo. In X×Y si definiscono come insiemi aperti (o semplicemente ‘aperti’) i p. cartesiani U×V, dove U è un aperto di X e V un aperto di Y, e inoltre tutti gli insiemi ottenibili come unione di questi insiemi prodotto. Questa topologia attribuita ad X×Y si chiama topologia p. (di quelle di X e di Y) e X×Y si chiama spazio topologico p. di X, Y. Per es., il piano euclideo è il p. topologico di due rette (piano e rette essendo provvisti delle topologie consuete): difatti ogni aperto del piano si può ottenere come unione di un numero finito o infinito di rettangoli (privati del bordo) con lati paralleli agli assi x, y, e ciascuno di tali rettangoli è appunto l’insieme p. di un intervallo aperto dell’asse x e di uno dell’asse y.

Per quanto riguarda il p. di trasformazioni ➔ trasformazione.