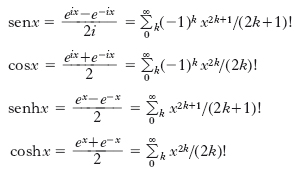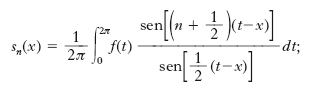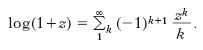serie

Successione ordinata e continua di elementi, concreti e astratti, dello stesso genere.

Ecologia

Successione delle comunità che si sostituiscono l’una all’altra in una regione. Le comunità di transizione sono dette stadi seriali, quella terminale stabile è chiamata climax. Poiché il climax varia in dipendenza di condizioni edafiche e climatiche da luogo a luogo, la s. può essere considerata indicatrice delle condizioni ecologiche locali.

Economia

Produzione in s. (o di massa)

Produzione di un grande numero di oggetti tutti uguali a un unico modello. Conseguenza della produzione in s. è la riduzione dei costi unitari, tanto più sensibile quanto maggiore è l’uso di procedimenti automatizzati; essa inoltre, garantendo la formazione di pezzi rigorosamente uguali, permette un rapido e sicuro montaggio, la sostituzione di pezzi e l’uso contemporaneo di questi in luoghi diversi con conseguente utile decentramento di lavorazione. D’altra parte, la produzione in s., traducendosi in un flusso abbondante e continuo di prodotti, richiede una domanda rilevante e in aumento; tale domanda deve essere accompagnata da una diminuzione dei prezzi per interessare i gruppi sociali a reddito debole, che sono sempre i più numerosi. L’industria può essere definita come una organizzazione del lavoro volta a ottenere produzioni in s. in tempi brevi.

Editoria

Nelle arti grafiche, l’insieme dei caratteri e dei segni necessari, distinti secondo la pendenza (tondi, corsivi), il tono (chiari, neretti, neri, nerissimi), la larghezza (stretti, normali, larghi, larghissimi) e la forma alfabetica (maiuscoli, maiuscoletti, minuscoli).

In biblioteconomia, pubblicazioni in s. (ingl. serials), le pubblicazioni, a stampa o no, che appaiono in fascicoli o volumi successivi, in genere collegati numericamente o cronologicamente, per una durata non predeterminata. Comprendono i periodici, i giornali, le pubblicazioni annuali (rapporti, annuari, repertori), le riviste, memorie, rendiconti, atti di società e le collezioni di monografie.

Geologia

S. geologica

L’insieme degli strati sedimentari considerati nella loro successione cronologica; come termine cronostratigrafico, la s. geologica rappresenta una unità, di rango superiore al piano, che indica una sequenza di formazioni sedimentarie e/o vulcaniche deposte una sull’altra in un dato intervallo di tempo (epoca: rappresenta la corrispettiva unità geocronologica) e in una data regione.

S. geologica normale

Successione stratigrafica di strati deposti secondo l’ordine di sovrapposizione corrispondente a quello originario di sedimentazione, dai più antichi ai più recenti.

S. geologica inversa

Successione stratigrafica di strati che ha subito un rovesciamento tettonico per cui i termini più antichi si trovano geometricamente al di sopra di quelli più recenti.

Matematica

In analisi, operazione eseguita su una successione di elementi a₀, a₁, ..., a_n, ... tra i quali abbia senso fare la somma; tale operazione consiste nell’associare alla successione una nuova successione s₀, s₁, ..., s_n, ... il cui elemento generico, che si dice somma parziale k-esima, o ridotta k-esima, è così definito: s_k=a₀+a₁+...+a_k. Si parla allora di s. formale, e si indica con il sim-

bolo ∑^∞_k=0a_k, o, talvolta con a₀+a₁+...+a_n+...,

a prescindere dal fatto che a esso si possa dare un significato concreto; gli elementi a_n si dicono i termini della s.; studiare la s. significa studiare la successione delle ridotte. Si chiama resto n-esimo di una s. la s. ottenuta dalla successione a_n+1, a_n+2, ...,

a_n+k, ... e si indica con R_n= ∑^∞_k=n+1a_k. Le ri-

dotte di tale s. resto si possono ottenere sottraendo a quelle della s. originaria la somma degli elementi da a₀ ad a_n. S. subordinata a una s. ottenuta dalla successione a₀, a₁, ..., a_n, ... è una qualsiasi s. ottenuta da una sottosuccessione di questa. Hanno particolare interesse le s. formali, per le quali ha senso eseguire l’operazione di limite sulla successione delle ridotte: per es., le s. i cui termini sono numeri (s. numeriche), matrici (s. di matrici), funzioni (s. di funzioni, e in particolare s. di potenze, s. trigonometriche ecc.). Il risultato di tale limite determina il carattere della s.: se il limite esiste, lo si chiama somma della s., lo si indica ancora con ∑^∞_k=0a_k=lim_n→∞ s_n, e si può dire intuitivamente che si è fatta la somma di infiniti termini. Il concetto di s. si può generalizzare, arrivando così alla s. bilatera, s. doppia, s. multipla, fino al concetto di famiglia sommabile.

S. numeriche

Tipi di serie

I termini della s. sono numeri reali o complessi; il limite della successione delle ridotte può esistere finito, o infinito, o non esistere, e la s. si dirà rispettivamente convergente, divergente, o indeterminata. La s. si dice anche regolare quando è convergente, oppure diverge a uno dei valori +∞, −∞; se non converge, né diverge e se è a termini reali viene chiamata oscillante. Il carattere di una s. è uguale a quello di ogni suo resto. Se una s. è regolare, vale la proprietà associativa della somma tra i suoi termini. La s. si dice assolutamente convergente se è convergente la s.

∑^∞_k=0∣a_k∣

dei moduli dei termini della s. data. Una s. assolutamente convergente è anche convergente; una s. che è convergente ma non assolutamente si dice semplicemente convergente. Scambiando tra loro un numero finito di termini della s., il carattere resta immutato, e in particolare la convergenza si avrà verso la stessa somma. Scambiandone invece un numero infinito ciò può non accadere, non vale cioè la proprietà commutativa. Questa vale solo per le s. assolutamente convergenti, mentre per una s. semplicemente convergente esiste sempre un modo di scambiare i termini tale da renderla convergente a un’altra qualsiasi somma finita, o addirittura renderla divergente o indeterminata (teorema di Riemann-Dini).

Criteri di convergenza e divergenza per una s. numerica

Data una s. numerica vale il seguente criterio generale di convergenza o criterio di Cauchy: condizione necessaria e sufficiente perché la s. sia convergente è che fissato comunque un numero ε>0 esista un indice ν, dipendente solo da ε, tale che per ogni n≥ν e per ogni intero p positivo sia

Ne segue che per la convergenza di una s. è necessario, ma non sufficiente, che il termine generale tenda a 0 (per p=1 si ha |a_n+1|<ε). Per le s. a termini reali, quando questi da un certo indice in poi sono dello stesso segno, valgono notevoli teoremi per determinarne il carattere: ci limitiamo alle s. a termini tutti positivi, che sono sempre regolari, essendo facile l’adattamento al caso più generale.

Criterio del rapporto (o di d’Alembert)

La s. converge se è lim_n→∞ (a_n+1/a_n)<1, diverge se è lim_n→∞ (a_n+1/a_n)>1.

Criterio della radice (dovuto a A.-L. Cauchy)

La s. converge se lim_n→∞ ⁿ√‾‾‾a_n<1, diverge se lim_n→∞ ⁿ√‾‾‾a_n>1.

Criterio di Raabe

Risolve alcuni casi in cui i limiti nei due criteri precedenti risultino uguali a 1 (➔ Raabe, Joseph Ludwig).

Criterio di Kummer

Include come casi particolari il criterio di Raabe e quello del rapporto (➔ Kummer, Ernst Eduard).

Primo criterio del confronto (dovuto a C.F. Gauss)

Se da un certo indice in poi i termini della s. sono minori dei corrispondenti termini di una s. convergente, la s. converge; se essi sono maggiori dei corrispondenti termini di una s. divergente, la s. diverge.

Secondo criterio del confronto

Due s. ∑^∞_k=0a_k, ∑^∞_k=0b_k tali che lim_n→∞ (a_n/b_n)=l≠0 hanno lo stesso carattere. Una s. a termini complessi ∑^∞_k=0d_k con d_n=a_n+ib_n converge se e solo se convergono le s. reali ∑^∞_k=0a_k e ∑^∞_k=0b_k, e analogamente per la convergenza assoluta. I criteri di convergenza per le s. a termini positivi sono criteri di convergenza assoluta per le s. a termini complessi.

Operazioni sulle serie

Considerate due s. numeriche convergenti ∑^∞_k=0a_k, ∑^∞_k=0b_k, le cui rispettive somme siano s, σ, la s. ∑^∞_k=0(a_k+b_k) risulta convergente e si chiama s. somma termine a termine; per essa si ha s+σ= ∑^∞_k=0(a_k+b_k). La s. ∑^∞_k=0(a_k−b_k) è anch’essa convergente e si dice s. differenza termine a termine; per essa si ha: s−σ= ∑^∞_k=0(a_k−b_k). Posto inoltre w_n = a_ob_n + a₁b_n-1 + … + a_n-1b₁ + a_nb₀, la s. ∑^∞_k=0w_k si dice s. prodotto secondo Cauchy, o per diagonali, delle due s. date. Si possono anche considerare altri modi di fare il prodotto. Non sempre la s. prodotto di due s. convergenti è convergente; se lo è, vale il teorema di Abel:

Una condizione sufficiente per la convergenza della s. prodotto è che una delle s. date sia assolutamente convergente (teorema di Mertens).

Sommabilità di una serie

Se una s. numerica non è convergente, non ha significato parlare di somma nel senso usuale, perché non esiste lim_n→∞ s_n. Tuttavia talvolta esistono procedimenti che permettono di associare alla s. un numero finito (somma generalizzata), tra cui quello di E. Cesaro, per il quale si considera il limite della media aritmetica delle prime n ridotte: lim_n→∞ (s₁+s₂+…+s_n)/n. Se una s. è convergente a una somma s, essa è anche sommabile secondo Cesaro, e la somma generalizzata vale s. Viceversa, se una s. ∑^∞_k=0a_k è sommabile secondo Cesaro con somma generalizzata s, e inoltre esiste un numero positivo K tale che |a_n|≤K/n, allora la s. data è convergente alla somma s (teorema di Hardy). Se due s. sono convergenti a s e σ rispettivamente, la s. prodotto, anche se non converge, è sommabile secondo Cesaro con somma generalizzata sσ. Con altro procedimento indicato da N.H. Abel, si considera il limite della somma della s. di potenze reali ∑^∞_k=0a_kρ^k al tendere di ρ a 1 da sinistra. Se la s. ∑^∞_k=0a_k è sommabile secondo Cesaro, lo è anche secondo Abel, con la stessa somma generalizzata (teorema di Frobenius); non sempre vale il viceversa.

S. bilatera

Si indica col simbolo ∑^∞_k=−∞a_k e si ha partendo dalle due successioni a₀, a₁, ..., a_n, ... e a_–1, a_–2, ..., a_–n,

e considerando le due s. ∑^∞_k=0a_k e ∑^∞_k=−1a_k;

se queste convergono a s e a σ rispettivamente, si dice che la s. bilatera converge a s+σ.

Esempi di s. numeriche

S. armonica

È la s.

tale s. è divergente, sia pure molto lentamente, anche se limn→∞ an=0. La s. armonica generalizzata è ∑∞k=1 1/kα dove α è un numero reale positivo; tale s. è convergente se α>1, è divergente se α≤1. La s. armonica a segni alterni è ∑∞k=1 (−1)k+1/k, essa è convergente, ma non assolutamente, in quanto la s. dei valori assoluti è divergente.

S. geometrica

È la s. ∑∞k=0a0qk dove q è un numero reale o complesso, la cui somma parziale n-esima è data da a0(1−qn+1)/(1−q), e pertanto la s. è convergente se |q|<1 e la sua somma vale a0−−−−−1−q ; se |q|=1 con q≠1 è indeterminata, se q=1 o |q|>1 diverge.

S. di funzioni

Tipo di s. i cui elementi sono delle funzioni f₁, f₂, ..., f_n, ... complesse o reali, tutte definite in uno stesso insieme di un conveniente spazio complesso o reale. Nel caso di una sola variabile si scrive ∑∞k=1 fk(x) e la s. assume denominazioni particolari se tali funzioni sono di tipo particolare (così, per es., s. di potenze, s. trigonometrica, s. ipergeometrica ecc.). Riferendoci per semplicità a una s. di funzioni di una variabile reale x, definite in uno stesso intervallo dell’asse reale, una s. di funzioni si dice semplicemente convergente, assolutamente convergente, divergente o indeterminata per un valore x = x0 nell’intervallo di definizione delle funzioni, se tale è la s. numerica ∑^∞_k=1 f_k(x₀). L’insieme dei valori di x in cui la s. di funzioni converge (supposto che ne esistano) si dice insieme di convergenza, e la somma della s. è una funzione di x definita in questo insieme. Secondo il criterio di convergenza per una s. di funzioni (o di Cauchy), condizione necessaria e sufficiente perché una s. di funzioni sia convergente per un valore x della variabile è che per ogni numero ε>0 prefissato esista un indice ν, dipendente da ε ed eventualmente da x, tale che per n≥ν e per ogni p≥0 sia

Una s. di funzioni si dice uniformemente convergente in un intervallo (a, b) se la condizione precedente è soddisfatta per ogni x di (a, b) con un ν indipendente da x; chiamando norma della funzione f l’estremo superiore dei moduli dei valori assunti da f in (a, b) e indicando tale norma con ∥f∥, si dice anche, equivalentemente, che la s. ∑^∞_k=0 f_k(x) converge uniformemente a f se per n≥ν è ∥∑^∞_k=0 f_k−f∥<ε. Una s. uniformemente convergente in un intervallo (a, b) è assolutamente convergente in ogni punto di (a, b). Una s. di funzioni si dice totalmente convergente in (a, b) se la s. delle norme dei suoi termini, ∑^∞_k=0 ∥f_k∥, è convergente; una s. totalmente convergente in (a, b) è anche ivi uniformemente convergente. Se ciascuna delle f_k(x) è continua in (a, b) e se la s. ∑^∞_k=0 f_k(x) è uniformemente convergente, la funzione somma è continua in (a, b).

Esempi di s. di funzioni

S. asintotica

S. di funzioni che costituisce uno sviluppo asintotico di una funzione f(x) la quale, per x→∞, tenda al valore a₀. È una s. del tipo ∑^∞_k=0 a_kx^−k che gode della proprietà che la somma dei suoi primi k termini rappresenta la funzione data f(x) con un errore dell’ordine di x^−k.

Serie binomiale

È lo sviluppo in s. di Maclaurin della funzione (1+x)ⁿ, con x reale o complesso, n reale ≠0. Si ha (1+x)ⁿ= ∑^∞_k=0(nk)x^k, dove il simbolo (nk) indica il coefficiente binomiale; tale s. è convergente per |x|≤1 se n>0, per |x|<1 se n<0; per x=1 converge anche se è −1<n<0; nel caso che n sia intero positivo o nullo la s. si riduce a una somma finita e quindi converge per ogni x.

S. di Dirichlet

S. del tipo ∑^∞_k=0a_ke^−λkx, dove x è complesso, gli a_k sono numeri complessi e i λ_k sono una successione monotona di numeri reali che tende a +∞. Ponendo e^−x=z si ha la s. ∑^∞_k=0a_kz^λk, e se i λ_k sono interi si ha una s. di potenze alcune delle quali (in numero finito) sono eventualmente negative.

S. esponenziale

È lo sviluppo in s. di Maclaurin della funzione e^x; si ha, con la convenzione

0!=1, e^x=∑^∞_k=0x^k/k!; tale s. converge per ogni x, reale o complesso. Per x = 1 si ha la s. fattoriale. Facendo combinazioni lineari di s. esponenziali si definiscono le funzioni circolari e iperboliche anche per x complesso, tramite le seguenti formule di Eulero:

S. di Fourier

Per una funzione reale y=f(x), è la s. trigonometrica

a₀/2+ ∑^∞_k=1 (a_k coskx+b_ksenkx), dove i coefficienti a_k e b_k, detti coefficienti di Fourier della funzione, sono dati da:

Se la s. si esprime nella forma ∑+∞k=−∞ckeikx i coefficienti di Fourier risultano ck= 1−−2π ∫2π0 f(x)e−ikxdx. Se una s. trigonometrica converge uniformemente in (0,2π), essa è necessariamente una s. di Fourier. Sotto ipotesi molto ampie, la s. di Fourier di una funzione f(x), periodica di periodo 2π converge alla funzione stessa nei punti di continuità di f(x) e alla media aritmetica dei suoi limiti destro e sinistro nei punti di discontinuità di prima specie (teorema di Dirichlet). La continuità e la periodicità di f(x) senza ulteriori ipotesi assicurano che la sua s. di Fourier è sommabile, secondo Cesaro e secondo Abel, con somma f(x). Per una funzione pari risultano nulli tutti i bk, per una funzione dispari lo sono gli ak. Se f(x) è a quadrato sommabile, cioè appartiene allo spazio L2[0,2π], la ridotta n-esima Sn(x) della sua s. di Fourier rende minimo l’errore quadratico medio, cioè

∫2π0 ∣f(x)−Sn(x)∣2dx;

ciò si esprime dicendo che la s. di Fourier converge in media di ordine 2 (o nello spazio L₂) alla f(x). A sua volta la ridotta n-esima si può esprimere tramite un integrale così formulato:

lo studio di tale integrale, detto integrale di Dirichlet, si riconduce allo studio di

con m reale. Tramite le s. di Fourier si possono approssimare anche funzioni generalmente continue non periodiche, definite su intervalli limitati, o anche su tutto l’asse reale purché ivi sommabili. In quest’ultimo caso la rappresentazione di f(x) si ha tramite il valore principale di Cauchy di un integrale doppio (contrassegnato con * ʃ), detto integrale di Fourier, ottenuto come limite di una s. di Fourier estesa a un intervallo limitato facendo tendere i suoi estremi all’infinito. Tale integrale, che vale

1−−2π *∫∞−∞ (∫∞−∞ f(t)cos[u(x−t)]dt)du, sotto opportune ipotesi coincide con la funzione f(x) dove questa è derivabile e con la media aritmetica dei suoi limiti destro e sinistro nei punti di discontinuità di prima specie dove esistono le derivate destra e sinistra (teorema di Fourier); l’ultimo fatto va sotto il nome di fenomeno di Gibbs. Tutte le considerazioni sopra esposte si estendono alle funzioni di più variabili, periodiche rispetto a ciascuna di esse, anche con periodi diversi; si fa uso in tal caso delle serie multiple e degli integrali multipli. Lo sviluppo di una funzione nella sua s. di Fourier si dice, con termine proveniente dall’acustica, sua analisi armonica (➔ armonico); ciò corrisponde a vedere la funzione come risultato di un sovrapporsi di infiniti fenomeni periodici con periodi e ampiezze sempre minori: infatti, sotto ampie ipotesi i coefficienti ak e bk tendono a 0 per k→∞ (teorema di Riemann). Tale metodo si applica anche a equazioni differenziali nello studio di oscillazioni di corde, membrane o circuiti elettrici e nella teoria del potenziale.

Serie di Fourier generalizzata

Data una funzione f(x) di L2[a,b], si dice sua s. di Fourier generalizzata una s. del tipo ∑^+∞_k=0c_kψ_k(x), dove le funzioni ψ_k(x) formano un sistema ortonormale in L₂[a,b], e dove i numeri c_k, che si dicono coefficienti di Fourier generalizzati, sono dati da

c_k =∫^b_a f(x)ψ_k(x)dx.

Per es., le funzioni 1−−−√‾‾‾‾2π, senkx−−−−−√‾‾‾‾π , coskx−−−−−√‾‾‾‾π , costituiscono, al variare di k, un particolare sistema ortonormale che dà la s. di Fourier usuale. Sotto opportune ipotesi, tra le quali la chiusura del sistema ortonormale, si hanno convergenze di vario tipo della s. di Fourier generalizzata verso la f(x).

S. ipergeometrica

Per tale tipo di s. ➔ ipergeometrica, serie.

S. di Laurent

È una s. bilatera di potenze di coefficienti

c_k= 1−−−−2πi ∫_C−−−−−f(s)−−−−−ds e con C circonferenza di centro x0 (➔ anche Laurent, Pierre-Alphonse)

(x−x₀)^k+1

La parte della s. con gli esponenti positivi si dice parte regolare, l’altra singolare, o principale. Se quest’ultima non è nulla, in x0 vi è una singolarità polare o essenziale a seconda che i coefficien­ti non nulli siano in numero finito o no. Se esiste solo la parte regolare

f^(k)(x₀)

risulta ck= −−−−−−−− e la s. di Laurent si ridu-

k!

ce a una s. di Taylor.

S. logaritmica. Nel campo complesso la funzione f(z)=log(1+z) ha infiniti valori per ogni z, tranne che per z=1 dove c’è un punto di diramazione. Quella determinazione di log(1+z) che per z=0 assume il valore 0 si dice determinazione principale e il suo sviluppo in s. di Maclaurin si dice s. logaritmica:

Tale s. converge per |x|<1 e nel punto x=1, dove si ottiene la s. armonica a segni alternati che ha quindi come somma log2.

S. di Maclaurin

Nome che prende la s. di Taylor quando il punto iniziale è l’origine del sistema di riferimento.

S. di potenze

È una s. del tipo ∑^∞_n=0a_n(x−x₀)ⁿ, o anche ∑^∞_n=0a_nxⁿ (nella variabile reale o complessa x), a seconda che il suo punto iniziale sia x₀ oppure 0. Una s. di potenze converge sempre nel suo punto iniziale; può convergere anche in altri punti, e anche in tutto il piano complesso (su tutto l’asse nel caso reale). Se x è complessa esiste comunque sempre un cerchio, detto cerchio di convergenza (per x reale si riduce a un intervallo), di centro il punto iniziale, all’interno del quale la s. converge assolutamente, mentre all’esterno diverge; sulla frontiera la convergenza può esserci in tutti i punti, o solo in alcuni, o in nessuno. Il suo raggio R (nel caso reale è la semilunghezza dell’intervallo) si dice raggio di convergenza e si usa dire che è nullo se la s. converge solo nel punto iniziale, oppure infinito se la s. converge in tutto il piano complesso; R può calcolarsi con la formula:

1

lim_n→∞ ⁿ√‾‾‾‾a_n = −−(teorema di Cauchy-Hadamard)

R

oppure

a_n+1 1

lim_n→∞ ∣−−−−−∣=−−(se tale limite esiste), con la

a_n R

convenzione che se i primi membri sono nulli il raggio è infinito e viceversa. Per la convergenza, valgono il teorema di Weierstrass (➔ Weierstrass, Karl Theodor Wilhelm) e il teorema di Abel (➔ Abel, Niels Henrik). Nella classe delle funzioni (analitiche) olomorfe e iniettive su un disco unitario (dette univalenti regolari) del tipo f(z)=z+ ∑^∞_n=2a_nzⁿ vale la congettura di Bieberbach (1916): |a_n|≤n per n≥2, dimostrata da L. de Branges nel 1984.

S. bilatera di potenze

S. di potenze del tipo ∑^+∞_k=−∞c_k(x−x₀)^k, che possiede quindi anche potenze negative. Se c_k=0 per i k negativi si rientra nelle s. ordinarie di potenze.

S. di Taylor

Per una funzione di variabile reale o complessa f(x) infinitamente derivabile in un punto x₀, è la s. di potenze

∑^∞_n=0a_n(x−x₀)ⁿ, dove a_n=f⁽ⁿ⁾(x₀)/n!. Se in un intorno di x₀ tale s. converge a f(x), la funzione si dice sviluppabile in s. di Taylor, o analitica nell’intorno. Ciò accade sotto ampie ipotesi, per es. se in tutto l’intorno le derivate di f(x) esistono e sono limitate in modulo da un numero M. Se x è complessa, la sviluppabilità di f(x) in s. di Taylor in un cerchio C è equivalente all’olomorfia nei punti interni a C. Nel caso di più variabili si hanno s. multiple i cui coefficienti sono derivate parziali; per es., per due variabili, la s. di Taylor di f(x,y) è

Lo sviluppo in s. di Taylor è utilissimo per lo studio delle funzioni non periodiche; le somme parziali di ordine uno e due di tale s. danno rispettivamente l’approssimazione lineare e quella quadratica.

S. trigonometrica

S. del tipo

dove a0, ak, bk sono numeri reali qualsiasi e x è una variabile reale. Si può anche scrivere, usando la funzione esponenziale nel campo complesso e le s. bilatere, sotto la forma ∑^+∞_k=−∞c_ke^ikx con c_k=(a_k−ib_k)/2,

e c_–k=(a_k+ib_k)/2. Se la s. converge nell’intervallo (0, 2π) essa converge su tutto l’asse reale, e la sua somma è una funzione periodica di periodo 2π. Con un semplice cambiamento di variabile si può rendere arbitrario il periodo. Le ridotte di una s. trigonometrica si dicono polinomi trigonometrici. Le s. trigonometriche, e in particolare le s. di Fourier, si prestano assai bene ad approssimare funzioni periodiche o con molte oscillazioni, o diverse da zero solo in intervalli limitati, quali si presentano in moltissimi fenomeni fisici.

Geometria

S. lineare

Fissata una curva algebrica piana C e un sistema lineare ΣR (di dimensione R) di curve algebriche dello stesso piano di C le quali non contengano tutte come parte la curva C, ciascuna di esse interseca su C un numero finito di n punti, costituenti un gruppo di punti Gn; le ∞R curve di Σ intersecano su C ∞r (r≤R) gruppi Gn; il loro insieme si dice s. lineare (di gruppi di punti) sopra la curva C, e si indica con gnr. I numeri n e r si dicono rispettivamente ordine e dimensione della s. lineare. Su una curva irriducibile esiste un numero minimo q (≥1) di punti che genera una s. lineare, e il numero p=q−1 si dice genere della curva. Una s. lineare per cui è r>n−p si dice speciale. Due gruppi Gn, G′n del medesimo numero di punti di C, si dicono linearmente equivalenti se appartengono a una medesima gnr. L’importanza delle s. lineari sta nel fatto che esse sono invarianti di fronte alle trasformazioni birazionali, in quanto i loro gruppi sono gli insiemi dei punti di C nei quali una funzione razionale, dipendente da r−1 parametri, assume lo stesso valore, cioè sono i gruppi di livello di una tale funzione. In questa forma il concetto si trasporta alle curve algebriche sghembe.

Musica

Nel sistema dodecafonico (➔ dodecafonia), l’elemento basilare, formato dal susseguirsi in un determinato ordine dei 12 suoni che compongono la scala cromatica temperata: appare nella forma fondamentale e in quelle per moto retrogrado, per moto contrario e per moto contrario del retrogrado.

Statistica

Si dice s. statistica una successione di dati statistici, distinti in corrispondenza delle modalità di un certo carattere qualitativo; se il carattere è quantitativo si ha una seriazione statistica. Questa è una successione numerica (detta meno propriamente solo seriazione), ciascun elemento della quale esprime il numero degli individui che presentano una determinata caratteristica (in particolare una modalità quantitativa) di un fenomeno collettivo; un esempio di seriazione statistica è dato dai numeri degli individui che presentano le varie stature: inferiore a 150 cm, tra 151 e 160 cm, ..., tra 191 e 200 cm, oltre 200 cm; questa seriazione statistica contiene 7 termini. In generale una seriazione è rappresentabile con un istogramma.

S. storica (o s. temporale)

Con tale espressione si indica un insieme ordinato di osservazioni (elementi della s. storica) relative a un carattere qualitativo xt; l’indice t ordina cronologicamente tali elementi e può essere un numero intero, nel qual caso la s. si dice discreta (per es., i valori giornalieri di chiusura di un’azione in una data borsa), oppure un numero reale variabile in un intervallo, nel qual caso la s. si dice continua (per es., la pressione atmosferica misurata in modo continuo).

Alcune s. storiche discrete sono costituite da elementi determinati per accumulazione nel tempo, come quelle relative al numero delle nascite calcolato mensilmente, e sono dette in tal caso s. di densità. Una classificazione di carattere statistico divide le s. storiche a seconda che posseggano o no il carattere di stazionarietà: una s. storica si dice s. stazionaria quando il valor medio x̄ e la varianza σ2x sono indipendenti dal tempo t e la covarianza di X con la stessa X traslata di un ritardo τ è una funzione γ(τ) che dipende da τ e non dal tempo t; la γ(τ) considerata come funzione del ritardo τ è detta funzione di autocovarianza. Nell’analisi delle s. storiche stazionarie è conveniente normalizzare tale funzione dividendola per la varianza σ2x e ottenendo in tal modo la funzione di autocorrelazione ρ(τ)= γ(τ)/σ2x che indica la correlazione esistente tra la X e sé stessa traslata temporalmente di τ, al variare di τ. Il grafico di tale funzione è detto correlogramma e in base a esso è possibile effettuare un’analisi delle caratteristiche interne della s. storica.

Se si ammette l’ipotesi che ogni s. storica sia una parte di un insieme infinito di elementi ordinati, è possibile utilizzare un teorema dovuto a H. Cramer (teorema di rappresentazione spettrale), con il quale si dimostra che ogni s. storica può essere rappresentata per mezzo di una ‘somma’ di infinite componenti cicliche aventi ciascuna ampiezza aleatoria ma periodo fisso. Data l’ortogonalità di queste, la varianza totale σ2x della s. storica è data dalla somma delle varianze delle singole componenti cicliche. La ripartizione della varianza tra queste componenti con frequenza angolare compresa tra −π e π è indicata dalla funzione di densità spettrale

che matematicamente è la trasformata di Fourier della funzione di autocovarianza. Il significato di tale funzione può essere compreso considerando che il suo integrale tra λ1 e λ2 rappresenta la parte di varianza della s. storica spiegata dalle componenti cicliche con frequenza angolare compresa tra λ1 e λ2. Per valutare la stima fˆ(λ) di f(λ) si usa generalmente la

per j=1,2,..., M, e con λj=πjM, che è una versione corretta della precedente tale da rendere asintoticamente consistente la stima. Le quantità σ̂x2 e γ̂(τ) sono stime campionarie della varianza e delle autocovarianze effettuate sugli elementi della s. storica. Il diagramma che rappresenta fˆ(λj) in funzione delle frequenze tra 0 e π è detto spettro, e dalla sua analisi, condotta identificando le frequenze alle quali lo spettro presenta dei massimi relativi (picchi), è possibile determinare le ciclicità più importanti presenti nella s. storica; l’area compresa al di sotto di un picco fornisce una misura relativa di questa ‘importanza’. Molte delle s. storiche che si incontrano nella tecnologia e nelle scienze fisiche sono stazionarie, come quelle relative alla temperatura o alla pressione misurate in un dato luogo; le s. storiche economiche sono invece essenzialmente non stazionarie, in quanto presentano generalmente valore medio e varianza crescenti o decrescenti nel tempo. Per poter attenuare la variazione della varianza è di uso comune effettuare una trasformazione logaritmica dei dati, mentre per eliminare la tendenza crescente o decrescente delle s. storiche la si suppone costituita dalla somma di una funzione non aleatoria del tempo, g(t), rappresentante la tendenza, e di una variabile statistica Yt stazionaria; si ottiene così il semplice modello Xt=g(t)+Yt che rende possibile l’analisi spettrale effettuata sulla Yt. Questa analisi è utile per individuare le caratteristiche cicliche di una s. storica economica, come le ciclicità congiunturali e le accidentalità. Le stagionalità sono oscillazioni che si ripetono annualmente nelle s. storiche e sono dovute a fattori connessi con i periodi festivi e in generale con il variare annuale del clima e delle abitudini; le ciclicità congiunturali sono invece conseguenza dell’alternarsi dei periodi di recessione e di sviluppo dell’economia, mentre le accidentalità sono il risultato delle interazioni tra il sistema economico e il fenomeno di cui la s. storica costituisce una misura.

Tecnica

Collegamento in s.

Connessione di più elementi (condensatori, resistori, generatori ecc.), omogenei o no, uno di seguito all’altro. In tale tipo di collegamento i vari bipoli collegati sono percorsi dalla medesima corrente; l’impedenza complessiva Z risulta pari alla somma delle impedenze:

[1] formula

essendo Z₁, Z₂, ..., Z_n le impedenze dei singoli elementi collegati. Se gli elementi collegati in s. sono polarizzati, il collegamento deve essere fatto in modo che risultino connessi insieme i poli eteronimi. Tale avvertenza vale in particolare per il collegamento in s. di più generatori di tensione continua: la forza elettromotrice (e la resistenza interna) della s. di generatori risulta allora pari alla somma delle forze elettromotrici (e delle resistenze interne) dei vari generatori collegati. Nel caso del collegamento in s. di più resistori, l’impedenza Z si riduce alla resistenza R e la [1] diviene: R=R₁+R₂+...+R_n. Se invece si collegano in s. più induttori l’impedenza Z si riduce alla sola reattanza induttiva e dalla [1] si ottiene: L=L₁+L₂+...+L_n, essendo L l’induttanza complessiva della s. e L₁, L₂, ..., L_n le induttanze dei vari induttori. Nel collegamento in s. di più condensatori, dette C₁, C₂, ..., C_n le capacità dei singoli condensatori e C la capacità complessiva, dalla [1], riducendosi l’impedenza Z alla reattanza capacitiva, si ha:

Eccitazione in s.

Tipo di eccitazione per le macchine a corrente continua (dinamo o motori), caratterizzato dal fatto che l’avvolgimento di eccitazione è collegato in s. con quello di indotto. Motore s. Denominazione di alcuni motori, sia per corrente continua sia per corrente alternata, del tipo monofase o trifase a collettore, caratterizzati dal fatto che gli avvolgimenti di statore e di rotore risultano collegati in s. (➔ motore).