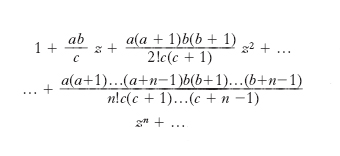ipergeometrica, serie

Nome dato da Eulero alla serie

,

dove a, b, c, z sono numeri complessi qualsivogliano (ma c è diverso da 0 e da un intero negativo). Essa converge assolutamente per | z | < 1. K.F. Gauss, che studiò per primo la serie i. (detta perciò anche serie di Gauss), chiamò a, b, c i parametri, z l’argomento, e ne indicò con F (a, b, c, z) la somma, detta funzione ipergeometrica. Tale funzione soddisfa l’equazione differenziale i.:

z(1−z)F″+[c−(a+b+1)z]F′−abF=0,

la quale ammette anche altre soluzioni, esprimibili però sempre mediante funzioni ipergeometriche. Casi particolari della serie i. sono la serie binomiale:

(1+z)^m=F(−m, 1, 1,−z),

e la serie logaritmica: ln (1+z)=−F(0, 1, 1, −z). Quando il parametro b tende all’infinito la funzione i. diviene, al limite, una funzione i. confluente che è soluzione dell’equazione i. confluente, ed è somma della serie i. confluente (la qualifica di ‘confluente’ è dovuta al fatto che, in questo passaggio al limite, due dei punti singolari dell’equazione confluiscono in uno solo). Dallo studio della serie i. sono scaturiti due dei più importanti capitoli della teoria delle funzioni: quello sulle equazioni differenziali lineari (I. L. Fuchs), e quello sulle funzioni automorfe (H. Poincaré, F. Klein).