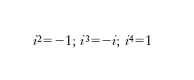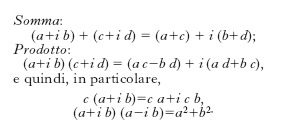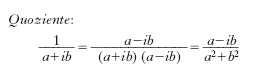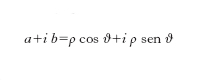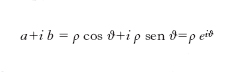complessi, numeri
Si chiama c. ogni numero della forma a + i b, essendo a e b due numeri reali relativi (positivi, negativi o anche nulli) e rappresentando il simbolo i (unità immaginaria o immaginario) la radice quadrata di −1; l’addendo a si chiama la parte reale, l’addendo i b la parte immaginaria, b il coefficiente dell’immaginario. Si opera sui numeri c. considerandoli come polinomi (a coefficienti reali) di 1° grado nel simbolo i e tenendo conto che le potenze di i sono:
ecc. In base a ciò si hanno le seguenti regole di calcolo (fig. 2):
Quoziente:
(purché non sia contemporaneamente a = 0, b = 0). A un numero complesso z=a+i b si può far corrispondere il numero z̄ =a−i b che si dice suo coniugato o il suo c. coniugato; tale corrispondenza è involutoria, ossia il coniugato di z̄ è z. Si osservi che la somma di un qualunque numero c. z e del suo coniugato, cioè z+z̄, è sempre un numero reale, e vale 2a; così pure il prodotto z z̄ è un numero reale, uguale ad a2+b2 (e perciò positivo o nullo) che si chiama norma di z; la sua radice quadrata positiva, √‾‾‾‾‾‾a2+‾‾b2, è il modulo di z.
Le operazioni definite soddisfano le consuete proprietà formali; l’insieme dei numeri c. è perciò un corpo commutativo o campo di numeri. È anzi il corpo algebrico, algebricamente chiuso, che si ottiene ampliando il corpo dei numeri reali, aggiungendo a esso una radice dell’equazione x2+1=0, irriducibile nel campo reale. In parole più semplici, i numeri c. sono una naturale e necessaria estensione del campo dei numeri reali, alla quale si è portati quando si vuole dare un senso all’operazione di estrazione della radice quadrata nel caso in cui il radicando è negativo.
Per l’origine storica dei numeri c. ➔ numero.
In un piano cartesiano, che prende il nome di piano c. o piano di Argand-Gauss o piano sfera, si fa corrispondere biunivocamente al numero a+i b il punto che ammette a come ascissa e b come ordinata (fig. 1). Risulta in tal modo subordinata una corrispondenza sia fra i numeri reali e i punti dell’asse x (asse reale), sia fra i numeri con parte reale nulla, cioè del tipo i b (detti numeri immaginari puri), e i punti dell’asse y (asse immaginario). Due numeri tra loro coniugati vengono rappresentati da punti in posizione simmetrica rispetto all’asse reale. Ove convenga, si può anche considerare come rappresentativo del numero c. a+i b il vettore che, applicato nell’origine O del piano c., ha come estremo il punto (a, b). Il modulo sopra definito del numero c. a+i b, ρ=√‾‾‾‾‾‾a2+‾‾b2 è allora uguale alla distanza dall’origine del punto rappresentativo del numero c.; l’angolo ϑ, che è definito (a meno di multipli di 2π) da cos ϑ=a/ρ, sen ϑ=b/ρ si chiama argomento (o anomalia) del numero c. e, più precisamente, si dice valore principale dell’argomento quel suo valore per cui è 0≤ϑ〈2π. Vale dunque la formula:
Tale rappresentazione trigonometrica del numero c., dovuta ad A. de Moivre, consente di vedere facilmente che modulo e argomento dell’inverso di un numero sono rispettivamente l’inverso e l’opposto di quelli del numero dato; e che il modulo e l’argomento di un prodotto sono uguali rispettivamente al prodotto dei moduli e alla somma degli argomenti dei fattori; in particolare si ha la cosiddetta formula di De Moivre, che esprime la potenza n-ma di un numero c.: (a+i b)n=[ρ (cos ϑ+i sen ϑ)]n=ρn (cos n ϑ+i sen n ϑ).
La rappresentazione geometrica dà un’immagine semplice e intuitiva dei numeri c. come vettori e permette d’interpretare la somma di due numeri c. come somma dei vettori che li rappresentano nel piano c. (fig. 2). La rappresentazione geometrica è inoltre uno strumento efficace per affrontare alcuni importanti problemi. Ricordiamo, per es., che le n radici complesse dell’unità positiva sono rappresentate, sul piano c., dai vertici di un poligono regolare di n lati, inscritto nella circonferenza di centro nell’origine e raggio 1; e che quindi la costruzione del poligono regolare di n lati è intimamente legata alla risoluzione (nel campo c.) dell’equazione xn=1 (➔ poligono). Una terza rappresentazione dei numeri c., è la rappresentazione esponenziale, che si ottiene da quella trigonometrica applicando la formula di Eulero: