vettore

Biologia

Organismo che trasporta un parassita (batterio patogeno, fungo, protozoo o virus) e lo trasferisce da un individuo (animale o Uomo) a un altro. Sono esempi comuni di v. alcuni animali ematofagi (che si nutrono di sangue), come pulci, zecche, zanzare, pipistrelli, capaci di trasmettere, mediante puntura o morso, determinate parassitosi, del cui agente patogeno rappresentano un ospite intermedio o definitivo.

In biologia molecolare, v. di clonazione, molecola di DNA a doppia elica, capace di replicarsi autonomamente in una cellula ospite, nella quale è inserito un altro frammento di DNA per formare una molecola ricombinante adatta alla clonazione. Con metodi di ingegneria genetica, qualsiasi gene può essere purificato e, una volta inserito in un v., si può duplicare in una cellula ospite in quantità illimitata. Quando il v. di clonazione può replicarsi in due o più organismi ospiti, prende il nome di v. navetta. I v. utilizzati per clonare geni sono diversi a seconda dell’ospite (batterio o cellula eucariote) dove il DNA viene fatto replicare. I v. di clonazione più usati si replicano nei batteri e sono i plasmidi, i batteriofagi e i cosmidi. A differenza dei v. plasmidici e fagici, i cosmidi non si trovano in natura ma sono costruiti combinando caratteristiche dei plasmidi e del batteriofago λ. I cromosomi artificiali di lievito (YAC) sono v. eucariotici che permettono la clonazione in lievito di frammenti di DNA molto lunghi e sono usati, per es., per costruire mappe di genomi complessi quali quello umano. Utilizzando Escherichia coli come ospite sono state sintetizzate, da geni inseriti in un v., le proteine del virus dell’afta epizootica nel bestiame e quelle del virus dell’epatite nell’Uomo utili per l’immunizzazione, enzimi quali l’insulina, ormoni (per es., la somatomedina) e l’attivatore tissutale del plasminogeno. Per studiare l’espressione di un gene già clonato è importante scegliere il sistema ospite-v. appropriato. I v. che dirigono tali sintesi proteiche programmate, denominati v. di espressione, sono modificati per consentire sia la replicazione del v. sia la sintesi di proteine in ospiti diversi. Per l’espressione di geni clonati in cellule di mammifero, i v. più usati sono derivati dal genoma del virus di scimmia SV40 e da quello del papilloma virus bovino. Anche i retrovirus (➔) possono funzionare come v.: v. retrovirali difettosi nella replicazione ma che possono essere trascritti in DNA e inseriti nel genoma dell’ospite possono diventare uno strumento efficace per la terapia genica di soggetti che presentano un difetto genico modificabile a livello dei tessuti somatici. Per la manipolazione genetica dei prodotti dell’agricoltura, il v. delle cellule vegetali più comunemente usato è il plasmide Ti, il cui ospite è Agrobacterium tumefaciens che si fonde con la cellula vegetale e vi trasferisce il DNA ricombinante (➔ transgenico).

Matematica e fisica

Ente caratterizzato, oltre che da un’intensità (o modulo), cioè da un valore numerico (o scalare), anche da una direzione e da un verso.

Grandezze vettoriali

L’origine del concetto di v. è da ricercare nella geometria e nella meccanica. Tale concetto è suggerito dallo studio delle caratteristiche di certe grandezze come gli spostamenti, le velocità, le forze che non possono essere descritte completamente da una sola quantità numerica, che ne misura l’entità, ma sono caratterizzate anche da un orientamento, cioè da una direzione e da un verso. Viene naturale assumere come rappresentante di una tale grandezza un segmento orientato AB avente una lunghezza, una direzione e un verso, in modo che la lunghezza rappresenti l’entità della grandezza, mentre direzione e verso siano quelli propri della grandezza in questione. Queste grandezze prendono il nome di grandezze vettoriali, in contrapposizione alle grandezze scalari, caratterizzate da una sola quantità numerica (come, per es., la massa, la temperatura ecc.). Con riferimento a un segmento orientato AB, il punto A prende il nome di origine e il punto B è l’estremo del segmento stesso. Due segmenti orientati equipollenti AB, A′B′ (aventi cioè in comune lunghezza, direzione e verso) rappresentano la stessa grandezza vettoriale e un v. è l’astratto di una classe di segmenti orientati equipollenti. Con ciò si vuole significare che un v. geometrico è un ente rappresentato indifferentemente da un segmento orientato AB o da qualsiasi altro segmento orientato equipollente ad AB; inoltre esiste un rappresentante del v. con l’origine in un punto comunque prefissato dello spazio.

Un v. si rappresenta con lo stesso simbolo di un segmento orientato che lo rappresenta, eventualmente sormontato da una freccia, cioè AB→ , oppure con una lettera in grassetto v, mentre con |AB| o con v si indicherà la sua lunghezza o modulo. Un v. v, pensato come l’astratto di una classe di segmenti orientati equipollenti, prende anche il nome di v. libero; per un v. libero è del tutto indifferente il punto di applicazione, cioè l’origine di un segmento orientato che lo rappresenti. Per contro un segmento orientato AB, avente l’origine nel punto A si chiama anche v. applicato (nel punto A), e si può pensare come l’insieme del v. v e del punto A (punto di applicazione); un v. applicato si indica con la notazione (A, v) o altra analoga. La considerazione dei v. applicati è essenziale agli effetti, per es., della rappresentazione delle forze per le quali non è indifferente la scelta del punto di applicazione.

Operazioni sui vettori

fig. I

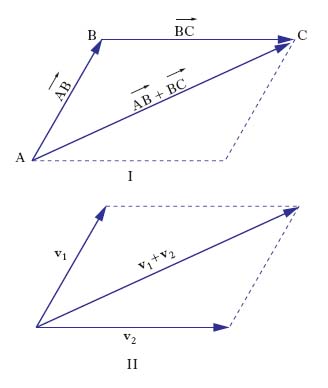
La nozione puramente matematica di v. è però quella di v. libero, o senz’altro di vettore. La sua importanza in matematica e nelle sue applicazioni è dovuta all’esistenza di certe operazioni che sono definite sui v. e che consentono di costruire un’algebra dei v. e di sviluppare un vero e proprio calcolo vettoriale. La prima operazione fondamentale è quella di composizione o somma di due v. secondo la regola del parallelogramma (suggerita dalla composizione degli spostamenti A→B e B→C: fig. I): il v. v₁+v ₂, somma dei due v. v₁ e v₂, è la diagonale del parallelogramma che ha i due v. come lati consecutivi uscenti dal vertice comune. Essa gode della proprietà commutativa e associativa, e cioè

v₁+v₂=v₂+v₁

(v₁+v₂)+v₃=v₁+(v₂+v₃).

La composizione si può eseguire anche su un sistema di un numero qualunque di v. e dà luogo al risultante del sistema; viceversa, ha spesso interesse la decomposizione di un v. in due o più v. componenti. Nell’operazione di somma di v. l’elemento neutro è il v. nullo, che si indica con 0: esso è rappresentato da un segmento orientato AA di lunghezza nulla; il v. opposto del v. v è invece quel v. v′ tale che

v+v′=0.

La seconda operazione è quella di prodotto di un v. v per uno scalare r (numero reale); il risultato è il vettore v′ che ha il modulo v′=|r|v, la stessa direzione di v e lo stesso verso oppure l’opposto a seconda che r sia positivo o negativo. Combinando le due operazioni, a partire dai v. v₁, ..., v_k e dagli scalari r₁, ..., r_k, si può costruire il v.

v=r₁v₁+...+r_kv_k

che si chiama combinazione lineare dei v. v₁, ..., v_k con i coefficienti r₁, ..., r_k.

Spazi vettoriali

La constatazione che in numerosi altri insiemi matematici è possibile introdurre in modo naturale delle operazioni formalmente simili alle due sopra dette per i v. (così accade, per es., per certi insiemi di matrici, insiemi di funzioni ecc.) ha condotto a uno studio sempre più astratto e generale delle proprietà algebriche dei v., e ha portato alla formulazione generale della nozione di spazio vettoriale (➔ spazio). Lo sviluppo della teoria degli spazi vettoriali introduce via via nozioni e proprietà relative ai v. che li costituiscono. Così accanto alla nozione di combinazione lineare di più v., compare subito quella di v. linearmente dipendenti (o indipendenti): più v. v₁, ..., v_k sono linearmente dipendenti se esistono k scalari r₁, ..., r_k non tutti nulli, tali che risulti

r₁v₁+...+r_kv_k=0

(una combinazione lineare di v₁, ..., v_k dà il v. nullo). I v. dati sono invece indipendenti quando non esiste alcuna combinazione lineare del tipo precedente. Per i v. geometrici la dipendenza lineare ha un significato immediato: due v. sono linearmente dipendenti se e solo se sono paralleli; tre v. sono dipendenti se e solo se sono complanari (cioè paralleli a uno stesso piano) ecc. Nello studio degli spazi vettoriali è fondamentale la nozione di base; si tratta di un insieme (non necessariamente unico) di v. c₁, ..., c_n linearmente indipendenti e tali che ogni v. v dello spazio si possa esprimere come loro combinazione lineare

v=v₁c₁+ ... + v _nc_n.

L’intero n è la dimensione dello spazio vettoriale, e ha un valore costante qualunque sia la base che si considera. Dire quindi che lo spazio dei v. geometrici ha dimensione 3 significa che in esso esistono tre v. linearmente indipendenti c₁, c₂, c₃, costituenti una base, e che ogni altro v. dello spazio si può esprimere come loro combinazione lineare. I coefficienti v₁, ..., v_n della combinazione lineare prendono il nome di componenti del v. v rispetto alla base prefissata. Così, se lo spazio ha dimensione 2, i v. hanno due componenti; se ha dimensione 3, i v. hanno tre componenti ecc.

Nell’ordinario spazio euclideo i v. hanno tre componenti, cioè sono rappresentabili con una terna ordinata di numeri; si scrive anche v≡(v₁, v₂, v₃). È molto importante osservare che, fissata una base, le componenti di un v. sono univocamente determinate; anzi c’è una corrispondenza biunivoca tra v. e n-ple ordinate di numero, cosicché, in un certo senso, la considerazione dei v. di uno spazio a n dimensioni può essere sostituita da quella delle n-ple di numeri. E ciò anche agli effetti delle operazioni sui v.: così, per es., il v. somma di due v. dati ha come componenti le somme delle componenti dei due addendi. Occorre però fare attenzione a non identificare i v. con le n-ple di numeri che ne rappresentano le componenti; infatti le componenti di un v. cambiano se si sceglie un’altra base, mentre il v. ha un significato intrinseco, del tutto indipendente dalla base. Non sempre però esiste una base formata da un numero finito n di v.; in tal caso lo spazio vettoriale ha dimensione infinita.

Quanto è stato detto finora vale in uno spazio vettoriale qualunque. Spesso lo spazio, e i suoi v., godono però di ulteriori proprietà che ne arricchiscono la struttura. Così accade, per es., per gli spazi vettoriali in cui è definito anche il prodotto interno, o prodotto scalare, tra vettori. Nel caso dei v. geometrici, il prodotto scalare di due v. a, b è dato dal prodotto dei moduli dei due v. per il coseno dell’angolo ϑ fra essi compreso o, in forma cartesiana, dalla somma dei prodotti delle componenti cartesiane omonime dei due v.:

a∙b=ab cosϑ =a_x∙b_x+a_y∙b_y+a_z∙b_z.

Il prodotto scalare di un v. v per il versore di una retta orientata r (ossia per il v. di lunghezza unitaria orientato come r) dà luogo alla componente v, di v secondo r. La forma intrinseca del prodotto scalare mette in evidenza che esso coincide col prodotto del modulo di un v. per la componente dell’altro secondo la direzione orientata del primo. L’annullarsi del prodotto scalare di due v. non nulli caratterizza l’ortogonalità dei due vettori. Il prodotto v. (o vettoriale o esterno) di due v. a, b è definito, nel caso dei v. dell’ordinario spazio a tre dimensioni, come il v. v=a×b che ha per modulo il prodotto ab senϑ dei moduli dei due v. per il seno dell’angolo fra essi compreso, direzione normale al piano individuato dai due v. applicati in uno stesso punto, verso tale che la terna a, b, v risulti levogira o anche, secondo altra convenzione, orientata come la terna costituita dai versori c₁, c₂, c₃ degli assi di riferimento. Note le componenti cartesiane di a e b, le componenti cartesiane del prodotto v. sono i minori principali estratti dalla matrice

quindi si ha

v=(a_yb_z−a_zb_y)c₁+(a_zb_x−a_xb_z)c₂+

+(axby−aybx)c3.

In base alla definizione risulta

a×b=−b×a,

di modo che il prodotto v. non è commutativo ma alternante. L’annullarsi del prodotto vettoriale di due v. non nulli caratterizza il parallelismo dei v. medesimi. Per tutti i prodotti suddetti valgono, con le sole eccezioni segnalate per il prodotto v., tutte le proprietà formali del prodotto ordinario. Su di essi, inoltre, come sul risultato delle altre operazioni sopra ricordate, non influisce la scelta dei punti di applicazione: si tratta di operazioni di fronte alle quali i v. vanno considerati in ogni caso come liberi. Non altrettanto può dirsi per il risultato di altre operazioni che hanno significato soltanto se riferite a v. applicati: è ciò che, per es., si verifica nel calcolo dei momenti (assiali o polari). La considerazione di operazioni e di enti legati ai punti di applicazione rientra, in modo specifico, nella teoria dei v. applicati. Osserviamo che le operazioni tra v. ora definite si possono tutte effettuare sia operando sulle componenti dei v., sia operando sui v. direttamente; poiché il v. è un ente dotato, a differenza delle sue componenti, di un significato intrinseco (indipendente cioè dal riferimento), i risultati ottenuti si prestano alla rappresentazione matematica e all’interpretazione fisica di fenomeni e di leggi; nello stesso tempo, per il fatto di operare su uno anziché su tre elementi, si ottiene una rappresentazione molto sintetica.

Rappresentazione vettoriale nella fisica

La rappresentazione vettoriale delle grandezze e la relativa trattazione con i metodi del calcolo vettoriale trovano largo impiego in fisica (particolarmente in meccanica) e in moltissime applicazioni della matematica. In fisica, i v. sono generalmente v. a tre (o più) componenti; a seconda delle esigenze, si può trattare sia di v. liberi (o semplicemente v.), sia di v. applicati.

Un particolare sistema di v. applicati è la coppia (eventualmente degenere, cioè a braccio nullo). Elementi fondamentali, di carattere globale, sono per un sistema di v. applicati il suo risultante R e il suo momento risultante M rispetto a un assegnato polo T. Nel passaggio da un polo T a un polo T′ il momento in generale varia, secondo la legge

M=M′+TT′×R;

fa eccezione il caso in cui sia R=0 (il caso, per es., di una coppia), nel quale il momento si presenta (al variare del polo) come un invariante. Un sistema a R≠0, comunque complesso, è generalmente riducibile, al più, al suo risultante applicato all’asse centrale e a una coppia di momento μ (agente quindi in un piano normale all’asse centrale). È importante notare che il passaggio da un qualunque sistema di v. applicati a un altro equivalente si può ottenere con le cosiddette operazioni elementari, che sostanzialmente sono: a) l’aggiunta o la soppressione di una o più coppie di braccio nullo; b) la sostituzione di un gruppo di v. tutti applicati in un punto con il loro risultante applicato allo stesso punto; è immediato constatare che ambedue le operazioni non alterano né il risultante né il momento risultante del sistema di vettori.

Medicina

In cardiografia, v. cardiaco è la rappresentazione delle forze elettriche create dal cuore durante il processo di attivazione; la sua grandezza esprime il momento del dipolo elettrico cui il cuore può essere assimilato, mentre la direzione verso cui esso punta ne indica l’orientamento. Poiché il v. cardiaco, in accordo con il variare della condizione elettrica del cuore, varia continuamente nel valore e nella direzione, con il termine v. istantaneo si indica il v. cardiaco nell’istante considerato. Il v. cardiaco medio rappresenta invece la media dei v. cardiaci istantanei che concorrono a definire un intero ciclo elettrocardiografico, o soltanto alcune fasi di esso. Il v. cardiaco può essere ricostruito a partire dai segnali elettrici rilevati con vari tipi di derivazioni e il suo variare durante il ciclo cardiaco può essere rappresentato in un grafico detto vettocardiogramma; la vettocardiografia è quindi lo studio dei v. cardiaci proiettati sul piano (vettocardiografia piana), o nello spazio (vettocardiografia spaziale).

Trasporti

Nella navigazione radar-assistita, il v. (o v. guida) è l’informazione o il comando teletrasmessi, con gli elementi di moto necessari per proseguire il volo in sicurezza o terminare la missione (direzione, verso, velocità, quota, posizione di riferimento), ad aereo o missile che non possa mantenere da solo la traiettoria stabilita.