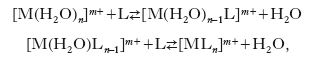stabilità

Chimica

Capacità di un composto o un sistema chimico di conservarsi invariato, di non subire modificazioni chimiche. Sono detti stabilizzatori (o sostanze stabilizzanti o solo stabilizzanti) le sostanze che, aggiunte a un’altra o in genere a un sistema chimico, tendono a renderlo più stabile, cioè ad assicurare la conservazione nel tempo del suo stato e delle sue proprietà: così, per es., l’acqua ossigenata, che tende a decomporsi facilmente sotto l’azione del calore, della luce, di particelle polverulente, si può conservare a lungo con l’aggiunta, come stabilizzatore, di piccole percentuali di acido fosforico o di urea. Costanti di s. Le costanti di equilibrio relative alle reazioni di formazione di un complesso. In soluzione acquosa la formazione di un complesso avviene mediante la sostituzione delle molecole di acqua coordinate intorno allo ione centrale, con i gruppi leganti ionici o molecolari. Nella soluzione coesistono perciò n equilibri del tipo

dove n e m sono rispettivamente il numero di coordinazione e la carica dello ione metallico M, mentre L indica il legante (supposto elettricamente neutro). Le n costanti di equilibrio delle suddette reazioni vengono denominate costanti di s. parziali. Quanto maggiore è il valore dell’i-esima di tali costanti (k_i), tanto più è favorita la formazione del relativo complesso. Le costanti di s. globali (β_i) sono invece definite come β_i=k₁k₂ ... k_i. Tutte le costanti di s. vengono espresse generalmente in termini di concentrazione e non di attività, per cui il loro valore dipende dalla forza ionica della soluzione oltre che dalla temperatura. Se il metallo e/o il legante sono coinvolti in altri equilibri, è utile introdurre la costante di s. condizionale, il cui valore dipende dalla concentrazione delle specie che danno vita agli equilibri secondari (per es., dal pH, se il legante ha proprietà basiche, come spesso accade).

Ecologia

La capacità intrinseca di un ecosistema di resistere ai cambiamenti. Un’ipotesi lega la s. delle comunità alla loro diversità di specie: se il flusso di energia all’interno della comunità può seguire più vie (per es., un predatore che ha più prede), allora l’interruzione di una delle vie (cioè la scomparsa di una preda) non fa altro che deviare il flusso verso un’altra direzione, senza che globalmente si verifichi alcun rallentamento o diminuzione del flusso stesso (cioè senza che la dinamica di popolazione del predatore venga modificata).

Secondo un’ipotesi alternativa, la diversità non genera s., in quanto l’incremento del numero di specie aumenta il numero e l’intensità delle interazioni che, a loro volta, generano ritardi nei processi demografici, destabilizzando il sistema. Sia la s. sia la struttura degli ecosistemi non hanno ancora una definizione che consenta misure oggettive delle comunità naturali.

Fisica

Condizione di ciò che è stabile, fermo, solido, durevole nel tempo. Specificatamente, proprietà di un sistema capace di sviluppare reazioni tali da compensare gli effetti di azioni esterne e mantenere quindi il suo assetto iniziale; tale significato, inteso come s. dell’equilibrio, si è esteso dalla meccanica ad altre discipline. In generale, parlando della s. in relazione a una grandezza fisica, s’intende l’entità, assoluta o relativa, delle variazioni di essa: per es., una s. (temporale) di 10–5 per una frequenza significa che quest’ultima è suscettibile di variare (nel tempo) dello 0,001%.

Instabilità

L’analisi delle proprietà di s. ha incentivato il parallelo studio della nozione di instabilità (➔), in cui si sono avuti importanti progressi. L’instabilità è definita solamente per un punto di equilibrio, sia per semplicità sia perché i risultati che si conoscono sono relativi a questo caso. Dato un sistema di equazioni differenziali della forma x′=f(t,x), e posto per semplicità nell’origine un punto di equilibrio del sistema, f(t,0)=0 per ogni t, si dice che l’origine è instabile se esiste ε>0 tale che per ogni dato iniziale x0≠0, detta x(t,x0) la soluzione dell’equazione x′=f(t,x) con dato iniziale x0, esiste un t tale che |x(t,x0)|>ε. La determinazione delle condizioni per cui un punto di equilibrio è instabile costituisce un problema di grande difficoltà: per es., nel caso meccanico, l’instabilità di un sistema conservativo avente un potenziale approssimabile attorno all’origine con una forma omogenea che può assumere anche valori negativi è stata dimostrata solo negli anni 1980, e in certi casi particolari.

Scienza dei sistemi

Il termine s. indica un’importante proprietà della risposta di un sistema dinamico, e cioè quella di evolvere con uno scostamento arbitrariamente limitato rispetto all’andamento nominale in seguito a perturbazioni opportunamente limitate sullo stato iniziale. Lo studio della s., che può essere inquadrato nell’ambito della teoria qualitativa delle equazioni differenziali (iniziato da J.-H. Poincaré intorno al 1880), si avvale ancora della formulazione dovuta al matematico russo A.M. Ljapunov, autore nel 1892 di un celebre trattato sulla s. del moto.

Tipi di stabilità

In particolare, si definiscono vari tipi di s., corrispondenti ai diversi tipi di risposta che possono essere presi in considerazione (risposta libera o forzata, nello stato o nell’uscita), ai diversi modi di reagire alle perturbazioni e alle esigenze più o meno stringenti da soddisfare. Per es., si ha la s. semplice di uno stato di equilibrio xe se, fissato un qualsivoglia intorno di xe, l’evoluzione libera nello stato si mantiene entro tale intorno, purché lo stato iniziale sia sufficientemente vicino a xe. Si ha invece la proprietà di s. asintotica per lo stato d’equilibrio xe se, oltre alla s. semplice, si ha anche la convergenza verso xe di ogni evoluzione libera nello stato avente origine in un opportuno intorno dello stato d’equilibrio, detto regione di s. asintotica. Se la regione di s. asintotica coincide con tutto lo spazio di stato, la s. asintotica è detta globale. Volendo poi caratterizzare la velocità di convergenza delle traiettorie di stato verso xe, si parla di s. esponenziale se, per stati iniziali sufficientemente vicini a xe, lo scostamento delle suddette traiettorie dallo stato di equilibrio è limitato, in norma, da un esponenziale decrescente.

Nel caso di sistemi dotati di rappresentazioni lineari, si può parlare direttamente di s. (semplice o asintotica) della rappresentazione. Infatti si dimostra facilmente che gli stati di equilibrio, che costituiscono in questo caso un sottospazio lineare dello spazio di stato, godono tutti delle stesse proprietà di stabilità. Inoltre, in presenza di s. asintotica, questa è sempre globale ed esponenziale, e riguarda l’origine dello spazio di stato che è in tal caso l’unico stato di equilibrio della rappresentazione. Accanto al tipo di s. appena descritto, basato sulla considerazione della risposta libera nello stato (e spesso indicato con il termine di s. interna), se ne definisce anche un altro, basato sulla considerazione della risposta forzata nell’uscita e denominato s. esterna. Un sistema si dice stabile esternamente se, a partire da ogni stato iniziale e sottoposto a ingressi limitati, risponde con uscite anch’esse limitate. Questo tipo di s. è anche detto s. BIBO (ingl. bounded input-bounded output «ingresso limitato-uscita limitata»).

Condizioni di stabilità

Poiché la s. è un requisito fondamentale per qualsiasi sistema fisico, è assai utile conoscere le condizioni che assicurano l’uno o l’altro tipo di s., al fine di poterne verificare il soddisfacimento in fase di analisi, ed eventualmente imporlo mediante la sintesi di un opportuno sistema di controllo. Particolare interesse riveste il caso di sistemi dotati di rappresentazioni lineari a dimensione finita, per i quali si possono dedurre facilmente condizioni di s., sotto forma di proprietà della matrice di transizione dello stato Φ(t, t0). Tale matrice consente di esprimere l’evoluzione libera dello stato x del sistema nella forma

dove x₀ è lo stato iniziale. È possibile dimostrare che la limitatezza della norma di Φ(t, t₀) (per ogni t>t₀) è da sola condizione necessaria e sufficiente per la s. semplice della rappresentazione e, aggiunta alla convergenza a zero della stessa Φ(t, t₀) per tempi indefinitamente crescenti, è condizione necessaria e sufficiente per la s. asintotica. Nel caso di rappresentazioni stazionarie, quanto detto si particolarizza a condizioni sugli autovalori della matrice dinamica A, che caratterizza la forma implicita della rappresentazione con lo spazio di stato. In particolare, per sistemi a tempo continuo, condizione necessaria e sufficiente per la s. asintotica della rappresentazione è che gli autovalori della matrice A abbiano parte reale strettamente minore di zero. Per la s. semplice tale condizione (necessaria e sufficiente) è verificata ammettendo la possibilità di parte reale nulla per eventuali autovalori a molteplicità geometrica unitaria.

Criteri di stabilità

I criteri di s. sono quei procedimenti che consentono la verifica delle suddette condizioni di s. senza richiedere il calcolo, più o meno esplicito, della risposta del sistema. Fra tali criteri, uno dei più utilizzati è il metodo diretto di Ljapunov. Per rappresentazioni stazionarie, a dimensione finita, a tempo continuo e regolari, tale metodo si basa sul fatto che uno stato di equilibrio x_e è stabile se e solo se esiste almeno una funzione dello stato, V(x), nulla in x_e e strettamente positiva in ogni altro punto di un intorno S di x_e, tale che la sua derivata rispetto al tempo, V̇(x), sia nulla in x_e e minore o uguale a zero in ogni altro punto dello stesso intorno S. Per i sistemi a tempo discreto l’enunciato rimane ugualmente valido, purché a V̇(x) si sostituisca ΔV(x), e cioè la variazione di V(x) in un intervallo di campionamento. L’importanza del criterio di Ljapunov risiede nella sua applicabilità a una vasta classe di sistemi (eventualmente dopo opportune modifiche alla sua formulazione); esso ha però lo svantaggio di non fornire una procedura automatica generale per l’individuazione di V(x) (funzione di Ljapunov), rendendo impossibile ogni conclusione circa la s. di x_e nel caso che non si riesca a trovare tale funzione, oppure a dimostrarne l’inesistenza mediante qualche criterio di instabilità.

Per i sistemi dotati di rappresentazione lineare, la s. può essere valutata anche mediante l’impiego di criteri atti a stabilire l’appartenenza delle radici di un polinomio a opportune regioni del piano complesso, in particolare al semipiano sinistro (criterio di Routh). Applicati al polinomio caratteristico della matrice A, tali criteri consentono di verificare, rispettivamente, la s. di sistemi a tempo continuo e a tempo discreto.

fig. 1A

Di particolare interesse nella teoria dei controlli automatici è infine il criterio di Nyquist che, sempre in caso di linearità, consente di valutare la s. di un sistema a retroazione unitaria sulla base delle proprietà di s. del sistema in catena aperta (➔ reazione). Tale criterio è basato sulla costruzione del diagramma polare del determinante della matrice di trasferimento ad anello aperto, F(s), valutato per s che varia sull’asse immaginario (s=jω) percorrendolo nel verso delle ω crescenti. Il numero di rotazioni che tale diagramma compie in verso antiorario intorno al punto (−1+j0) è infatti pari alla differenza fra il numero di poli a parte reale positiva del sistema ad anello aperto e quello dei poli a parte reale positiva del sistema ad anello chiuso. In particolare, un sistema asintoticamente stabile ad anello aperto rimane tale ad anello chiuso se e solo se il diagramma polare del determinante di F(jω) non circonda il punto (−1+j0) (criterio ridotto di Nyquist: fig. 1A). L’applicazione del criterio descritto (nella sua forma completa o ridotta) è particolarmente semplice nel caso di sistema con un solo ingresso e una sola uscita: in tal caso, infatti, il determinante di F(jω) coincide con la funzione F(jω) stessa.

Oltre che sulla s. in sé, il criterio di Nyquist consente di trarre conclusioni sul persistere di detta proprietà in presenza di perturbazioni sui parametri del sistema (proprietà di robustezza della s.). Per es., nel caso di sistemi a un ingresso e un’uscita, all’aumentare del guadagno K di F(jω), il suo diagramma polare viene amplificato fino eventualmente a circondare il punto critico (−1+j0) (fig. 1B). Sulla base del criterio descritto, è possibile dunque individuare gli intervalli di valori di K per cui il sistema ad anello chiuso è stabile asintoticamente. A tal proposito, un sistema viene detto a s. regolare se esiste un solo valore critico per il guadagno ad anello aperto, K_c, per il quale si è al limite di s., cosicché il sistema ad anello chiuso è stabile per valori di K inferiori a K_c e instabile per valori superiori.

Margini di stabilità

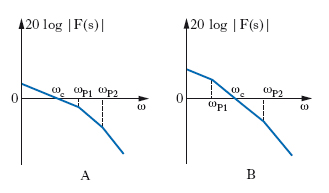
Per sistemi a s. regolare è possibile introdurre, sempre sulla base del criterio di Nyquist, dei margini di s., ovvero opportune misure della prossimità del sistema alla situazione di limite di stabilità. In particolare, si definisce il margine di guadagno come il logaritmo del rapporto tra il guadagno critico del sistema e il suo guadagno attuale. Il margine di fase si definisce invece come la differenza tra la fase di F(jω) e la fase critica (−π) corrispondente alla pulsazione critica ω_c, calcolata nel punto in cui il modulo di F(jω) è unitario.

fig. 2

Spesso si analizza il diagramma asintotico del modulo di F(s), ottenuto (fig. 2) riportando in ascissa su scala logaritmica le pulsazioni ω e in ordinata 20 log₁₀ ∣F(s)∣. Il diagramma è formato da una spezzata con i vertici in corrispondenza degli zeri e dei poli di F(s) ed è costruibile facilmente perché in corrispondenza di uno zero o di un polo si ha una variazione di pendenza di 20 dB per decade; il diagramma è detto asintotico perché ∣F(s)∣ tenderebbe a ciascuna retta della spezzata se non intervenisse un cambiamento di pendenza. Spesso, anziché calcolare il valore della fase in corrispondenza di ω_c, punto di intersezione con l’asse delle ascisse, si controlla che tale intersezione avvenga con pendenza inferiore a 20 dB per decade, il che garantisce che la fase è lontana da 180°.

Politologia

In materia di sicurezza internazionale, situazione in cui non giova ad alcuna delle parti di una disputa far ricorso alla forza armata. La s. strategica è definita come l’eliminazione dei vantaggi che ciascuna parte potrebbe percepire nel colpire per prima in una crisi. Quindi diventa essenziale che le potenze nucleari siano in condizione non tanto di usare per prime o più efficacemente le proprie armi, quanto di poter replicare a un eventuale primo uso nemico in ogni possibile circostanza. Il concetto di s. viene talvolta anche applicato in campo convenzionale, dove denota una situazione in cui le capacità difensive delle parti sono palesemente superiori a quelle offensive, precludendo qualunque vantaggio a un potenziale attaccante.

In senso geopolitico, situazione in cui i principali attori internazionali (Stati, movimenti di liberazione) e in particolar modo le maggiori potenze, non si adoperano per un mutamento violento dello statu quo, ma per una sua graduale evoluzione.

Tecnica

In scienza delle costruzioni, per s. di una struttura s’intende genericamente la sua proprietà di resistere nel tempo e in condizioni statiche soddisfacenti alle sollecitazioni cui essa è soggetta; con riferimento a tale significato si parla anche di verifica di s. (sia in sede di progetto, sia in sede di controllo di una costruzione esistente). La verifica di s. consiste nel valutare le tensioni interne della struttura con i metodi della scienza delle costruzioni e nell’accertare che esse risultino non maggiori dei corrispondenti carichi ammissibili di sicurezza.

Con significato più restrittivo, per struttura stabile s’intende una struttura esente dal pericolo dei fenomeni d’instabilità elastica per effetto delle forze cui essa è soggetta. In questo secondo caso s’intende parlare della s. dell’equilibrio elastico della struttura, cioè dell’equilibrio tra le forze esterne e le tensioni interne. Lo studio della s. elastica può in sostanza essere ricondotto a quello generale della s. meccanica, salvo a tener conto, oltreché delle forze esterne agenti sul sistema, anche delle tensioni interne che in esso si generano per effetto delle prime. Le tensioni interne costituiscono in ogni caso un insieme equilibrato di forze, ma quando si rinunci allo schema di perfetta rigidità, il loro intervento diviene essenziale nella considerazione dell’energia totale del sistema.