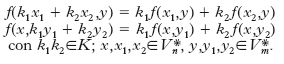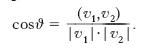spazio

spazio Sostantivo polisenso che designa in generale un’estensione compresa tra due o più punti di riferimento. Può essere variamente interpretato a seconda che lo si consideri dal punto di vista filosofico, psicologico, geometrico, fisico, astronomico, geografico, architettonico, pittorico, astronautico e industriale.

Astronomia

Con riferimento ai corpi celesti, o anche a mezzi artificiali, l’ambiente, il luogo in cui essi sono e si muovono. In particolare: s. terrestre, o circumterrestre, quello a non grande distanza dalla Terra, divisibile in s. atmosferico e s. extraatmosferico; s. planetario, o interplanetario, quello occupato dal Sistema solare; s. interstellare, la parte dell’Universo non occupata da stelle.

La navigazione spaziale è l’insieme delle conoscenze e delle tecniche necessarie per far viaggiare nello s. che circonda la Terra veicoli con equipaggio o con soli strumenti (➔ astronautica; navigazione).

La fisica spaziale è la branca dell’astrofisica e, più in generale, della fisica, che si avvale di sperimentazioni effettuate con satelliti artificiali (➔ satellite) e sonde spaziali (➔ sonda). Diversamente da altre discipline, la fisica spaziale non ha un suo tema specifico di ricerca, ma è piuttosto legata a una tecnica di indagine. Oggi, essa svolge un ruolo di primaria importanza in tutti i settori dell’astrofisica. Gli esperimenti di cui si occupa la fisica spaziale possono essere distinti in due grandi categorie. Il primo tipo utilizza satelliti artificiali per eseguire misurazioni in condizioni più favorevoli di quelle esistenti sulla Terra (assenza di atmosfera, gravità quasi nulla). Nella maggior parte dei casi, il satellite rappresenta un vero e proprio osservatorio astronomico dal quale, per es., si possono rivelare onde elettromagnetiche, provenienti da sorgenti celesti, in bande dello spettro non osservabili da Terra a causa dell’assorbimento atmosferico. Il secondo tipo di esperimenti è indirizzato all’esplorazione diretta, in loco, del Sistema solare.

S. aereo Quello in cui si svolge la navigazione aerea e spaziale, con specifico riferimento alle norme di diritto nazionale e internazionale che la regolano, nelle quali si distingue uno s. atmosferico, sovrastante il territorio di uno Stato e compreso nella sua sfera di sovranità, e uno s. extra-atmosferico, che si trova al di là dell’atmosfera e in cui è possibile il volo orbitale tramite lo sfruttamento della meccanica celeste.

S. atmosferico Spazio in cui si svolge la navigazione aerea. In base all’art. 1 della Convenzione di Chicago sull’aviazione civile internazionale del 7 dicembre 1944, la sovranità dello Stato si estende allo s. atmosferico sovrastante il suo territorio, compreso il mare territoriale. Tali diritti sovrani non si estendono invece allo s. sovrastante l’alto mare e gli spazi inappropriabili. Non vi sono modalità concordate tra gli Stati sulla delimitazione dello s. atmosferico; mentre in senso orizzontale la sovranità dello Stato trova un limite nello s. sottoposto alla sovranità di un altro Stato territoriale confinante, in senso verticale, non esiste una precisa delimitazione. Per ragioni pratiche, si assume tuttavia che il limite estremo dello s. atmosferico è rappresentato dall’altezza massima che può essere raggiunta da un aeromobile in volo.

Regime dello s. atmosferico. - L’attraversamento dello s. di uno Stato è soggetto al consenso e all’autorizzazione di quest’ultimo. Lo Stato territoriale può regolare, mediante la conclusione di specifici accordi internazionali, il passaggio nel proprio s., consentendo o impedendo l’ingresso ad aerei di altri Stati. Nello s. sovrastante l’alto mare e altri s. internazionalizzati vige invece libertà di sorvolo, sebbene sia invalsa la prassi da parte degli Stati costieri di definire delle ‘zone di identificazione’. Gli aerei che entrano in dette zone e che sono diretti verso le coste hanno l’obbligo di sottoporsi all’identificazione, alla localizzazione e ad altre misure di controllo. In tale s. aereo, la libertà di sorvolo può subire delle limitazioni dettate da esigenze di difesa dello Stato territoriale.

S. extra-atmosferico Non esiste una precisa linea di delimitazione tra s. atmosferico e s. extra-atmosferico. Si assume tuttavia che essa si collochi al più basso perigeo raggiungibile da un satellite terrestre, che, a seconda delle diverse opinioni degli Stati, è compreso tra 84 e 110 km al di sopra del livello del mare. Il lancio del primo satellite russo Sputnik il 4 ottobre 1957 e la corsa allo s. a scopi di difesa militare ha determinato una rapida evoluzione della disciplina giuridica dello s. extra-atmosferico. Il regime giuridico è costituito da un nucleo di principi generali, consolidatosi nel diritto internazionale tra il 1961 e il 1967, e da un insieme di norme contenute nei cinque trattati spaziali elaborati nell’ambito delle Nazioni Unite: il Trattato sullo spazio esterno del 1967, che regola le attività degli Stati nell’esplorazione e l’uso dello s. extra-atmosferico; l’Accordo sul salvataggio degli astronauti del 1968; la Convenzione sulla responsabilità per danni causati da oggetti spaziali del 1972; la Convenzione sulla registrazione degli oggetti lanciati nello spazio del 1975; l’Accordo relativo alle attività degli Stati sulla Luna e gli altri corpi celesti del 1979.

Regime dello spazio extra-atmosferico. - Il regime giuridico si fonda essenzialmente sul principio in base al quale lo spazio e i corpi celesti non sono soggetti a occupazione o appropriazione statale. L’esplorazione e l’utilizzazione dello s. costituiscono appannaggio dell’umanità intera e gli Stati devono cooperare nelle attività spaziali. Nello s. gli Stati sono responsabili per tutte le attività, proprie e svolte dai privati con la loro autorizzazione e sotto il loro controllo; essi sono tenuti alla registrazione degli oggetti spaziali lanciati in orbita.

Le attività spaziali per considerarsi lecite devono essere pacifiche. L’attività militare non è vietata, purché sia un’attività non aggressiva e conforme al principio di denuclearizzazione dello spazio.

Filosofia

Lo s. nel pensiero antico e medievale

Si può distinguere la problematica storica sul concetto di s. individuando due punti di vista: per il primo, lo s. è inteso come qualità relativa alla posizione degli oggetti materiali nel mondo; per il secondo lo s. è inteso come contenitore di tutti gli oggetti materiali. Tracce di una concezione dello s. quale contenitore degli oggetti materiali si possono ritrovare nella tradizione pitagorica e nella teoria atomistica del vuoto. Al pitagorico Archita è attribuita una teoria sulla natura primaria dello s., luogo (τόπος) di tutti i corpi e necessario per la loro stessa sussistenza. L’ipotesi atomistica riguarda invece l’esistenza di un infinito vuoto (κενόν) che contiene atomi indivisibili, costituenti, col loro aggregarsi, gli oggetti corporei. Il vuoto degli atomisti ha inoltre la funzione, secondo la testimonianza di Aristotele, di permettere il movimento degli atomi e dei corpi da essi composti.

La concezione del luogo esposta da Aristotele nel 4° libro della Fisica rientra, al contrario, sotto il primo dei due punti di vista sopra elencati. Il luogo, definito come la ‘superficie interna del corpo contenente’, compete a ogni singolo corpo materiale e, seppure esso è per definizione ‘diverso’ dal corpo che contiene, non è pensabile senza un corpo contenuto. A differenza di quanto accade nella concezione dello s. dei pitagorici e degli atomisti, non è il corpo ad avere bisogno dello s. per essere collocato ma, al contrario, se non si desse corpo, non si darebbe neppure il ‘luogo’ che lo contiene. Non esiste in Aristotele una teoria dello s. globale; all’interno del mondo si identificano i singoli luoghi semplicemente sommati e giustapposti, non costituenti uno s. unitario. Questi luoghi sono ordinati gerarchicamente in quanto a ognuno dei quattro elementi che costituiscono la sfera sublunare (terra, acqua, aria e fuoco) è assegnato un ‘luogo naturale’ verso cui ogni elemento tende per natura a tornare quando ne sia stato allontanato con la violenza. Il moto rettilineo, proprio solo del mondo sublunare, si giustifica quindi per la necessità di ricostituire l’equilibrio statico dei quattro elementi quando esso sia stato violentemente alterato. Al di sopra della sfera lunare le sfere celesti, muovendo eternamente in circolo per loro natura, non si allontanano mai dal loro luogo e non danno adito, con ciò, ad alcuno squilibrio. Nei cieli è quindi impensabile il moto rettilineo; la materia perfetta (quintessenza) che costituisce le sfere celesti possiede per natura un moto più perfetto, simile alla quiete in quanto non implica traslazione.

Le tesi di Aristotele posero una pesante ipoteca allo sviluppo dei concetti di luogo e di moto in età successiva. Sulla via che conduce al prevalere delle tesi relative a uno s. unitario contenitore dei corpi materiali riveste notevole importanza la trattazione di Filopono, commentatore cristiano di Aristotele (6° sec. d.C.); egli, nel suo commento al 4° libro della Fisica, elabora una teoria dello s. interno nettamente antitetica a quella aristotelica. Filopono contrappone alla definizione aristotelica del luogo come ‘superficie del corpo contenente’ la sua definizione del luogo come ‘intervallo’ (διάστημα) tridimensionale, corrispondente, come misura, al volume dell’oggetto ‘locato’; questo vuoto ricettacolo, in cui il corpo è contenuto, è incorporeo e permane immutato qualora il corpo ne esca. Una volta applicata questa definizione al luogo dell’intero mondo materiale, ne risulta un’unica estensione tridimensionale incorporea al cui interno si collocano i singoli corpi che ne occupano via via porzioni diverse. Cade con ciò per Filopono ogni distinzione qualitativa di luoghi naturali, impensabili in una estensione puramente tridimensionale; lo s. non possiede di per sé un ‘alto’ e un ‘basso’, una ‘destra’ e una ‘sinistra’, ma i corpi occupano le posizioni che sono state loro assegnate da Dio all’atto della creazione e tendono ‘naturalmente’ a mantenerle.

Al punto di vista opposto, cioè alla dottrina dello s. come qualità relativa alla posizione degli oggetti materiali, si ispira invece l’analisi del neoplatonico Damascio (6° sec. d.C.), per il quale il luogo o s. non è altro che la misura della relazione posizionale delle diverse parti di un oggetto o dell’oggetto nei confronti di altri. Questa ‘posizione’ è inerente e inseparabile dall’oggetto stesso. Contrariamente all’ambigua tesi di Aristotele, per cui, pur non dandosi luogo vuoto, il luogo è pur sempre ‘diverso’ dal suo contenuto e ‘permane’ quando questo se ne allontani, nella più rigida analisi di Damascio la posizione di un corpo in moto, per quante posizioni nuove esso assuma, non diventa mai posizione di un altro oggetto; essa, infatti, è semplice qualità del suo entrare in relazione con altri oggetti e non possiede quindi un’esistenza indipendente.

Lo s. nel pensiero rinascimentale e moderno

Telesio. La fioritura di nuove teorie sullo s., ricostruite anche sulla base della polemica antiaristotelica di Filopono, è databile al Rinascimento. B. Telesio oppone alla concezione di Aristotele la tesi di uno s. unitario privo di differenziazioni qualitative e di direzioni privilegiate: il moto dei corpi si giustifica integralmente guardando alle loro caratteristiche fisiche e alla tendenza a unirsi che è propria dei corpi simili. Nello s. omogeneo i corpi di simile natura sono attratti da forze simpatetiche, e i dissimili respinti da reciproche antipatie. A un’analoga concezione perviene G. Bruno, che procede altresì ad affermare l’infinità di questo s. vuoto, vanificando con ciò ancor più integralmente la pretesa scolastica d’identificare in esso direzioni e punti di riferimento fissi e assoluti.

Con F. Patrizi da Cherso il problema dello s. assume connotazioni metafisico-teologiche più complesse. Lo s. telesiano, che Patrizi accetta, fuoriesce dallo schema della metafisica aristotelica ponendosi in un rapporto problematico con la divinità: esso è prima creatura, senza la quale il mondo creato non avrebbe potuto sussistere. Patrizi giunge ad affermare la ‘parentela’ (cognatio) dello s. e della luce, prima manifestazione del suo Dio, neoplatonico, supponendo l’ipotesi di una derivazione dello s. da Dio nei termini di un rapporto di emanazione extratemporale e non di creazione nel tempo.

Galileo. Ben lontano da audaci ed eterodosse speculazioni metafisiche, G. Galilei mantenne al contrario ben fermi all’interno della sua fisica nuova alcuni presupposti tradizionali, fra cui una concezione dello s. non omogeneo e anisotropo. La tesi della comune ‘gravità’ di tutti i corpi materiali, non più distinguibili in pesanti e leggeri, e l’identificazione, quindi, di un’unica direzione ‘naturale’ nel moto all’ingiù avvicina Galileo piuttosto a Lucrezio che ad Aristotele, ma non toglie che il moto rettilineo dei corpi seguiti a essere distinto in ‘naturale’ e ‘violento’, e che sia lo s. a dirigere il moto naturale. All’interno di questa concezione si spiega come mai Galileo non sia potuto pervenire alla formulazione corretta della legge d’inerzia pur avendone individuato tutti gli altri presupposti.

Descartes e la scuola di Cambridge. D’altro canto R. Descartes, nella sua rigorosa riduzione del mondo fisico alle caratteristiche della geometria, perviene alla riduzione della materia a pura tridimensionalità, identificandola perciò con l’estensione in lunghezza, larghezza e profondità. Ciò gli consente, una volta liberata la materia da ogni altra qualità, di descriverne il comportamento in termini puramente meccanici, ma l’identificazione di estensione (s.) e materia impedisce altresì di concepire l’esistenza del vuoto e quindi d’intendere il movimento se non in termini puramente relativi. In un mondo pieno di materia estesa il moto non può essere che mutamento dei rapporti di posizione dei corpi.

Contro la tesi cartesiana, muovendo dal filone speculativo di ascendenza neoplatonica rappresentato da Patrizi da Cherso, elabora la sua teoria dello s. uno dei più illustri rappresentanti della scuola di Cambridge, H. More. Contro l’identificazione cartesiana di materia ed estensione More afferma l’attribuibilità dell’estensione anche alle sostanze spirituali, che altrimenti verrebbero negate, in quanto esistenti ‘in nessun luogo’. L’estensione immateriale in cui tutte le sostanze materiali e immateriali sono collocate, lo s. infinito, uniforme, indivisibile che tutto contiene, è il punto di riferimento immobile rispetto al quale è possibile identificare il moto ‘vero’ di un corpo e la quiete ‘vera’ di un altro, risolvendo l’assurdo problema che Descartes aveva aperto con la sua teoria del moto relativo. Questo s., analogamente a quanto si è visto in Patrizi, possiede una serie di caratteristiche (infinità, indivisibilità, unità ecc.) che consentono di supporre l’identificazione con l’infinito estendersi reale di Dio nel mondo. Il Dio provvidente della tradizione cristiana è ‘fisicamente’ presente nel mondo, o meglio ‘contiene’ in sé il mondo creato estendendosi a costituire lo s. infinito.

Newton, gli empiristi inglesi e Leibniz. È ormai accettata la dipendenza da queste teorie di More del concetto di s. assoluto elaborato da I. Newton. A partire da un’analoga polemica nei confronti di Descartes, Newton perviene alla definizione dello s. assoluto, infinito, omogeneo, isotropo, indivisibile, base immobile del movimento inerziale rettilineo dei corpi materiali, unico possibile parametro di misura dei moti veri e assoluti. Attraverso lo s. assoluto si trasmette altresì la forza gravitazionale che tiene unito in una compagine ordinata il cosmo planetario; dall’analisi di questa funzione che lo s. assume in relazione alla gravità, Newton desume la sua identificazione con l’infinito ‘esser presente’ di Dio, definendo lo s. assoluto come ‘sensorio’ di Dio. Con la teoria newtoniana dello s. assoluto, accettata da gran parte dei fisici del suo tempo, il punto di vista relativo allo s. come universale contenitore dei corpi sembra segnare un trionfo, seppure non incontrastato.

È soprattutto in sede epistemologica che il concetto newtoniano subisce più serie critiche, proponendosi da parte degli empiristi inglesi, J. Locke, G. Berkeley e D. Hume, e di G.W. Leibniz, seppure a partire da diversi presupposti, un’interpretazione soggettivistica della nozione di spazio. Per Leibniz il concetto di s. è un’elaborazione ideale che sorge dalla considerazione del mutare dei rapporti reciproci dei corpi. Per Locke l’idea complessa di s. nasce dalla correlazione mentale di idee semplici provenienti da sensazioni visive e tattili; per Berkeley la percezione dello s. è impossibile senza una serie di sensazioni visive e tattili, quali il colore, la figura ecc., del tutto soggettive, che vengono astratte dalla mente a costituire un’idea di cui non ci è affatto garantita la realtà extramentale; per Hume l’idea generale di s. non deriva da alcuna impressione individuale ma sorge dalla correlazione di gruppi di impressioni considerate come coesistenti.

Kant. Con queste tesi la validità fisica e metafisica del concetto newtoniano di s. come entità reale viene messa seriamente in discussione, aprendosi la via alla soluzione critica kantiana. Negando il carattere di realtà assoluta dello s. fisico ma nel contempo negando che esso possa risolversi in semplice astrazione di dati empirici, I. Kant definisce lo s. come «intuizione pura a priori», forma pura delle intuizioni del senso esterno: lo s. rappresenta la condizione necessaria per intuire gli oggetti come esterni a noi, ma nulla può dirci circa la realtà dei rapporti tra gli oggetti nel momento i cui essi siano considerati in sé.

Il concetto di s. dall’Ottocento a Einstein

Nel 19° sec. sono principalmente i matematici e i fisici che si rivolgono alla ricerca delle concezioni dello s., attraverso l’uso di strumenti concettuali altamente specializzati.

La matematica. Proprio all’inizio del secolo C.F. Gauss, contrapponendosi alle idee di Kant, rivendica alla conoscenza geometrica delle proprietà dello s. il carattere di conoscenza empirica, mentre il calcolo e l’analisi conserverebbero il carattere di conoscenze a priori.

Il problema dei fondamenti della geometria euclidea assume intanto nei primi decenni dell’Ottocento un aspetto completamente nuovo: fra i 5 postulati da cui Euclide aveva fatto discendere tutta la costruzione razionale della geometria, il quinto, cosiddetto delle parallele, era stato oggetto di studio già nel Seicento a causa della complessità nei riguardi degli altri, complessità che alimentava le ricerche per ridurlo agli altri o per lo meno a postulati più semplici. Il quinto postulato afferma che per un punto esterno a una retta si può condurre a essa una e una sola parallela. Si cercava di provarne la validità e necessità mostrando come la sua negazione portasse a risultati logicamente assurdi o in contrasto con il senso comune. Agli inizi del 19° sec. le ricerche assumono una direzione completamente nuova. N. Lobačevskij ritiene in un primo tempo di poter giungere a dimostrare il postulato delle parallele, e solo in seguito ai tentativi infruttuosi si convince che una geometria non euclidea è logicamente compatibile quanto la geometria di Euclide. Anche J. Bolyai, ungherese, scrive nel 1829 un lavoro in cui mostra come si possa costruire una geometria indipendente dal postulato delle parallele, meritando le lodi di Gauss, che era giunto per conto suo alle stesse conclusioni ma non le aveva pubblicate temendo di suscitare incomprensioni. Gauss dà inizio a un filone di ricerca che impronterà di sé tutta la fisica e la matematica moderna. Con l’affermazione di una possibilità logica di strutturare le proprietà dello s. in modo diverso da quello ormai tradizionalmente collegato alla geometria di Euclide, egli apre autorevolmente il problema del rapporto fra geometria e s. fisico e avvia l’indirizzo di ricerca delle geometrie differenziali, che offriranno in seguito all’indagine geometrica strumenti raffinatissimi, tali da rendere la geometria un metodo d’indagine delle proprietà spaziali altrettanto, se non più, potente del calcolo e dell’analisi numerica.

Queste prospettive sono realizzate da B. Riemann che effettua una feconda sintesi fra i metodi analitici e sintetici della matematica. Per Riemann lo s. è una struttura tridimensionale, ma il sistema di assiomi della sua geometria non è dato a priori. Riuscendo a scoprire altri tipi di s. prima non previsti, il metodo analitico di Riemann si è mostrato più fecondo dei metodi sintetici con cui si era arrivati alle geometrie non euclidee.

La fisica. Oltre alla matematica, anche le altre scienze positive entrano a metà Ottocento nel campo delle indagini sulla natura dello s.; emblematica l’opera di H.L. von Helmholtz, che studia il problema dello s. non soltanto come matematico ma anche come fisiologo, psicologo, fisico, e ne fa il punto focale di tutte le sue ricerche.

Le idee sul rapporto fra s. e oggetti in esso contenuti ricevono, a metà Ottocento, un contributo innovatore anche da una direzione imprevista, la fisica del campo elettromagnetico. M. Faraday mostra che i fenomeni elettrici e magnetici si spiegano molto meglio se si ammette che le forze elettromagnetiche possono esistere per sé, senza attribuire la loro origine a un ente materiale (come l’etere). Nella sua arditissima concezione si tende anzi a considerare la materia come una concentrazione di forze attrattive e repulsive. La fisica del campo viene matematizzata da W. Thomson e da J.C. Maxwell.

L’interesse dei fisici al problema dello s. si manifesta anche nell’approfondimento della comprensione del significato del principio d’inerzia. Nella formulazione di questo principio da parte di L. Lange nel 1885, si nota già un decisivo superamento della concezione newtoniana dello s. assoluto, in direzione di una diversa comprensione moderna del rapporto fra teoria fisica ed esperienza.

Geometria dello s. fisico. Il problema del rapporto fra matematica ed esperienza viene affrontato in modo singolare dal matematico F. Klein, la cui risposta ai problemi della teoria dello s. e della geometria si trova nella teoria dei gruppi di trasformazione, presentata nel suo programma di ricerche del 1872, detto programma di Erlangen. Il concetto di gruppo, insieme di operazioni astratte dotate di proprietà caratteristiche, è uno dei concetti più importanti della matematica moderna. Ogni geometria, secondo Klein, è, nel suo significato più vero e generale, una teoria delle proprietà degli invarianti rispetto a un certo gruppo di trasformazioni. Non c’è alcun limite nel pensare tipi diversi di trasformazioni, e così la varietà di geometrie possibili è illimitata. Nella nuova concezione della geometria di Klein la lontananza dal senso comune non è caratteristica della sola geometria non euclidea, ma appartiene già alla differenza fra il mondo dell’ordinaria percezione sensoriale e quello delle idee geometriche. Il successo di questa teoria mette in luce alla fine dell’Ottocento come nella matematica pura non vi sia alcuna necessità logica che obblighi a pensare soltanto uno s. a tre dimensioni. Il problema del perché lo s. percettivo sembri avere solo tre dimensioni sarà considerato d’ora in poi come un problema riguardante la fisiologia, la psicologia, la fisica.

A. Einstein mostra con la sua ‘relatività speciale’ del 1905 che la misura del tempo presenta quelle stesse caratteristiche di relatività rispetto ai sistemi di riferimento e al loro stato di moto che si credevano prima uniche prerogative dello spazio. H. Minkowsky interpreta questi risultati mediante una fisica quadridimensionale, un formalismo in cui il tempo figura sullo stesso piano delle dimensioni spaziali.

La quasi infinita libertà d’invenzione di nuove teorie geometriche e fisiche che sembra affacciarsi così alla mente umana è interpretata in modo particolare dalla filosofia del convenzionalismo, di cui è illustre esponente H. Poincaré. Poincaré nega la possibilità di formulare conclusioni sulle caratteristiche della geometria dello s. fisico. La scelta di una geometria è per Poincaré solo un problema di scelta motivata e concordata fra gli scienziati, cioè una scelta convenzionale. L’esperimento non può dirci niente sulla struttura dello s., ma solo sulle relazioni che passano fra gli oggetti materiali, e noi scegliamo sempre quella geometria che ci permette di formulare nel modo più semplice le leggi di natura. Coerentemente a queste sue idee, Poincaré è convinto che la geometria euclidea rimarrà sempre la favorita nelle teorie scientifiche.

Egli è smentito in questa sua previsione dal successo della teoria della ‘relatività generale’ di Einstein del 1916. Secondo questa teoria è la presenza della materia che modifica la geometria dello s.: la gravitazione deve essere inclusa nella struttura geometrica dello s.-tempo. In linea di principio, un osservatore potrebbe scegliere di continuare a considerare euclidea la struttura dello s.-tempo e ad attribuire alla gravità la deviazione dalla linea retta nel moto dei corpi. La scelta della relatività generale di includere la gravitazione nella geometria non rende soltanto la teoria logicamente più semplice e compatta, ma conduce anche a nuove previsioni, quelle della deflessione della luce nella vicinanza della materia, e all’interpretazione di fenomeni già noti, come l’avanzamento del perielio del pianeta Mercurio, che non sono spiegati dalla teoria newtoniana della gravitazione.

Geografia

Il concetto di s. entra formalmente nel dibattito sul pensiero geografico all’inizio del 20° sec., quando C. Vallaux (1911) lo qualifica in base al numero più o meno ampio di caratteri fisici, la cui diversità e le cui compenetrazioni si dispiegano sulla superficie terrestre. Alla fine degli anni 1930, R. Hartshorne, nell’ambito di una visione ‘corologica’ della geografia, individua il fulcro della disciplina nell’integrazione funzionale di fenomeni nello s., inteso come campo dell’organizzazione umana. Ancora, negli anni 1050, F.K. Schaefer affermava come unico oggetto della geografia le ‘relazioni spaziali’. Dunque lo s. geografico sarebbe costituito da quelle porzioni di superficie terrestre che presentano condizioni tali da rendere possibile l’insediamento, in forme organizzate, delle società umane.

Dallo s. assoluto proprio del determinismo naturalistico ed espresso cartograficamente, per ciascun punto, da una coppia di valori delle coordinate geografiche (latitudine e longitudine) si transita, così, allo s. come prodotto sociale, in cui la posizione relativa di ciascun punto è data dalle sue condizioni produttive, relazionali, di valore fondiario ecc. (D. Harvey). Sotto questo profilo, lo s. geografico è caratterizzato da una serie di discontinuità, che ne articolano i diversi ambiti configurando la struttura organizzativa del territorio, la cui complessità è data dalla compresenza e interazione di elementi fisici, storici, culturali, politici e funzionali. Ne derivano, per le diverse parti dello s. geografico, differenti traiettorie di sviluppo. Per tali aspetti, la concezione di s. in geografia si lega sempre più strettamente a quella di regione (➔), nell’ottica funzionalista e sistemica.

Lo s. geografico rimane comunque distinto dallo s. economico inteso come campo di forze o, più specificamente, come «insieme di relazioni astratte» (F. Perroux) di tipo matematico. Perciò l’avvento della ‘geografia quantitativa’ ha acceso un ulteriore forte dibattito in merito all’applicazione di modelli statistici alle realtà territoriali, da cui è derivata la cosiddetta ‘analisi spaziale’. Si è sottolineato, da parte dei geografi, come alcune tecniche di analisi statistica, quali quella di autocorrelazione o di convergenza spaziotemporale, debbano considerarsi utili strumenti di indagine, ma non possano in alcun modo surrogare l’interpretazione dello s. fondata sulla dinamica dei processi di organizzazione antropica, a loro volta strettamente motivati da fattori sociali e comportamentali.

Matematica

S. ordinario Lo s. nel quale viviamo, le cui proprietà geometriche gli hanno fatto attribuire la qualifica di euclideo. Il termine è poi passato a indicare, in matematica, altri enti, in qualche modo analoghi allo s. ordinario, dotati o no delle medesime proprietà.

Nozione di spazio

Inizialmente il termine s. indicava esclusivamente l’ambiente della geometria euclidea classica, ritenuta come l’unica ‘vera’, e nata dal desiderio di astrazione delle proprietà di estensione, di forma e di mutua posizione degli oggetti osservabili dall’uomo. Caduta tale concezione con l’avvento delle geometrie non euclidee (19° sec.), constatata cioè la compatibilità logica di altre geometrie diverse da quella euclidea, la nozione di s., nel più ampio contesto di una revisione dei fondamenti della geometria, ha assunto un ruolo non più assoluto, ma relativo al particolare tipo di geometria che si intende sviluppare. Così D. Hilbert nelle Grundlagen der Geometrie (1899) ha realizzato la sistemazione razionale della geometria in un sistema ipotetico-deduttivo (➔ sistema) ricorrendo a un insieme di postulati che legano i concetti di punto, retta e piano assunti come primitivi e definiti solo implicitamente dai postulati stessi. In tale contesto lo s., come insieme dei punti, rette e piani ha una struttura non unica, ma dipendente dal sistema di postulati che viene messo a base della geometria; a seconda dei casi si ha allora la struttura di s. proiettivo, s. metrico, s. grafico, s. vettoriale ecc. Secondo tale visuale un insieme di elementi di natura arbitraria può assumere la struttura di s. se è possibile introdurre in quell’insieme i postulati che caratterizzano quella struttura, cioè quel tipo di spazio.

Negli s. che sono stati fin qui nominati (s. proiettivo ecc.) i postulati consentono di riconoscere nell’insieme alcune delle proprietà dello s. della geometria euclidea; essi sono in definitiva abbastanza vicini alla comune intuizione geometrica. In altri casi invece la struttura dello s. ne è lontana. È questo il caso degli s. funzionali (insiemi di funzioni in cui è definita una opportuna nozione di ‘distanza’ tra due elementi, cioè due funzioni pensate come punti dello s., oppure una nozione di ‘vicinanza’ tra due elementi) e più generalmente degli s. topologici astratti. In questi ultimi gli elementi dello s. sono soggetti soltanto a delle relazioni che traducono in vario modo il concetto di vicinanza, intorno, distanza ecc. Con riferimento a un qualunque tipo di s., si definiscono i sottospazi di un dato s., come particolari suoi sottoinsiemi che hanno una struttura dello stesso tipo dello s. ambiente e a quest’ultima strettamente legata; le relazioni esistenti tra i sottospazi di un dato s., che dipendono evidentemente dai postulati che caratterizzano lo s. ambiente, e variano quindi da s. a s., servono in ogni caso validamente a descrivere la struttura dello s. ambiente.

Solo in alcuni casi è possibile definire un intero n (non negativo) da intendere come dimensione dello s. stesso, che fornisca un’indicazione del numero dei parametri da cui dipende la determinazione di un elemento dello s.; quando n>3 si parla di s. a più dimensioni, s. n-dimensionale o iperspazio. Spesso accade infine che in un dato insieme, pensato come s., siano simultaneamente presenti due diverse strutture di s., generalmente collegate tra loro; così, per es., l’ordinario s. euclideo possiede in modo naturale la struttura di s. euclideo (legata alla presenza delle coordinate cartesiane) e una struttura di s. topologico (che permette di parlare di continuità ecc.) la cui fusione fornisce l’ambiente naturale per sviluppare la teoria delle funzioni di variabile reale.

Tipologie di spazi

S. affine. La struttura di s. affine in un insieme è essenzialmente legata all’esistenza di un sistema di riferimento affine, che si può concepire come un riferimento euclideo non necessariamente ortogonale monometrico, o per meglio dire nel quale si prescinda da queste ultime condizioni. In uno s. affine dunque non si potrà parlare di ortogonalità, di distanze, di circonferenze ecc. (proprietà metriche), ma solo di proprietà affini come l’incidenza, il parallelismo, l’esistenza di parallelogrammi ecc. Un modello dello s. affine a 3 dimensioni è fornito dall’ordinario s. euclideo, nel quale si prescinda dalle proprietà metriche; in esso i punti hanno 3 coordinate (x, y, z), i sottospazi (rette, piani) sono rappresentati da equazioni lineari in x, y, z ecc. A differenza di quanto accade in uno s. proiettivo, due sottospazi di dimensioni complementari possono non essere incidenti (per es., nello s. affine a tre dimensioni un piano e una retta paralleli).

S. di Banach. È uno s. vettoriale normato, che sia anche completo nel senso che ogni successione di Cauchy converge a un punto dello s. stesso. Un esempio è fornito dallo s. euclideo En, con l’ordinaria metrica euclidea. La parte più importante della teoria degli s. di Banach viene però sviluppata in vista delle applicazioni allo studio degli s. funzionali e degli operatori in essi definiti.

S. euclideo (o n-dimensionale euclideo o iperspazio euclideo). Concetto che comprende quelli di piano e di s. della geometria elementare. In esso si chiama punto un insieme ordinato di n numeri x1, x2, ..., xn, reali o complessi a seconda che lo s. sia reale o complesso, detti coordinate del punto; si definisce come distanza di due punti (x1, x2, ..., xn), (y1, y2, ..., yn), l’espressione

e si chiama iperpiano l’insieme dei punti le cui coordinate soddisfano un’equazione lineare del tipo

(dove le a0 ... an sono delle costanti); l’intero n si dice dimensione dello spazio. Nella topologia si indica con Rn o En, nella geometria proiettiva con Sn. È evidente che si ottiene generalizzando lo s. ordinario (n=3), pensato riferito a una terna cartesiana ortogonale e monometrica. Per n=1 si ha la retta euclidea, per n=2 il piano euclideo ecc. La geometria analitica elementare, ordinariamente sviluppata in uno s. euclideo a 2 e 3 dimensioni, si estende facilmente a uno s. euclideo di dimensione qualunque. Oltre alla formula della distanza di due punti già citata, si possono scrivere le condizioni analitiche per esprimere il parallelismo, la perpendicolarità, le misure degli angoli, le aree ecc., analoghe a quelle tridimensionali.

S. fibrato. In geometria differenziale, nozione che generalizza quella di varietà prodotto di due varietà differenziabili (➔ varietà). Se V e V′ sono due varietà differenziabili e V×V′=W è il loro prodotto, esistono due mappe naturali (dette proiezioni), rispettivamente π: W→V e π′: W→V′, con la proprietà che per ogni x ∈ V la restrizione di π′ all’insieme π−1(x) è una mappa biunivoca di π−1(x) su V′, mentre la mappa inversa di V′ in W è un diffeomorfismo. Al variare di x in V l’immagine di V′ nella precedente mappa fornisce una fibrazione di W. Uno s. fibrato S si ottiene generalizzando la situazione ora descritta, e precisamente considerando una varietà B, detta base, al posto di V, una varietà F detta fibra al posto di V′ e associando a esse delle mappe (soddisfacenti opportune condizioni): una mappa π:S→B detta proiezione, e delle mappe di A×F in S (dove A è un aperto variabile in un ricoprimento di B). La varietà S risulta così essere fibrata mediante un sistema di sottovarietà diffeomorfe a F, pur senza essere in generale prodotto di B per F. Essa prende il nome di s. fibrato (o semplicemente fibrato) di base B e fibra F; nel caso particolare S=B×F si parla di fibrato banale. Per sezione di un fibrato si intende una mappa differenziabile σ:B→S tale che la composizione πσ sia l’identità su B.

Particolare importanza in geometria differenziale hanno alcune classi speciali di fibrati: tra questi i fibrati vettoriali, in cui la fibra è uno spazio vettoriale Vn a n dimensioni, come i fibrati tangenti e cotangenti a una varietà differenziabile.

S. di Fréchet. È uno s. metrico i cui elementi sono le successioni di numeri (reali o complessi) (x1, x2, ..., xn, ...) e nel quale si definisce come distanza di due elementi (x1, x2, ..., xn, ...), (y1, y2, ..., yn, ...) l’espressione

è uno s. limitato, perché la distanza di due suoi elementi qualunque è minore di e−1 (≅1,7 ...).

S. funzionale. S. astratto i cui elementi (punti) sono funzioni di un determinato tipo, nel quale viene introdotta una topologia (cioè sostanzialmente una nozione di intorno), con criteri che variano da un caso all’altro, sì da rendere lo s. stesso uno s. topologico. Esempi notevoli di s. funzionali sono lo s. di Banach, lo s. di Fréchet e l’insieme delle funzioni definite su uno s. topologico localmente compatto dotato della misura di Radon. Rispetto alla misura si definisce una famiglia normale di funzioni o funzioni ortonormali.

S. di Galois (o s. lineare finito). È uno s. proiettivo formato da un numero finito di punti, costruito sopra un corpo K che sia un campo di Galois (corpo necessariamente finito con q=ph elementi, essendo p un numero primo, e h>1). Le proprietà di geometria che si sviluppano in uno s. di Galois sono essenzialmente legate a questioni aritmetiche dipendenti dagli interi p e h; il loro studio può condurre a questioni di teoria dei numeri. Tra le questioni tipiche: determinazione del numero dei punti e del numero dei sottospazi di data dimensione dello s. ambiente, e più in generale del numero dei punti di una curva o di una varietà algebrica; studio di gruppi (finiti) di collineazioni e di omografie; studio dei k-archi nel piano (e di k-calotte nello s.) cioè di insiemi di k punti a due a due non allineati, e loro classificazione.

S. di Hausdorff. S. topologico costruito mediante opportuni assiomi di separazione. La corrispondente topologia si chiama topologia di Hausdorff.

S. di Hilbert. È caso particolare di uno s. di Banach nel quale la norma di un elemento si può derivare dal prodotto interno. Precisamente uno s. di Hilbert è uno s. vettoriale dotato di un prodotto interno (a, b) di due elementi, e dotato in conseguenza della norma ∥a∥=√‾‾‾‾‾‾(a, a); inoltre si deve trattare di uno s. di Banach nel senso che lo s. deve essere completo (ogni successione di Cauchy deve convergere. Oltre allo s. euclideo En, si può dare come esempio di s. di Hilbert lo s. delle successioni di numeri reali (x1, x2, ...) tali che sia convergente

la serie ∑^∞_k=1∣x_k∣²; il prodotto interno è ∑^∞_k=1x_ky_k

e la norma è √‾‾‾‾‾‾∑^∞_k=1∣x_k∣²‾‾‾. Questo esempio si

può riguardare come uno s. euclideo a infinite dimensioni. In tale s. si chiama cubo (o mattone) di Hilbert il sottoinsieme costituito dalla totalità delle successioni tali che 0≤x_i≤2^–i, (i=1, 2, ...). La teoria degli s. di Hilbert è stata di grande impulso per la costruzione della teoria degli s. funzionali e dei relativi operatori; è utilizzata anche in fisica, e in particolare in meccanica quantistica, dove gli stati di un sistema sono descritti da vettori di uno s. di Hilbert.

S. metrico (o distanziale). S. nel quale è definita una distanza d tra due qualunque elementi x, y tale che d(x, y)=0 se e solo se x=y, e d(x, y)+d(x, z)≥d(y, z) (relazione triangolare). La distanza permette di definire l’intorno di un punto x₀ di raggio r>0 come l’insieme degli elementi x tali che valga la relazione d(x₀, x)<r; in conseguenza è possibile introdurre una nozione di continuità e in definitiva una struttura di s. topologico (ogni s. metrico è dunque uno s. topologico, anche se non vale il viceversa).

S. misurabile. S. nel quale è assegnata una σ-algebra di sottoinsiemi, cioè un’algebra booleana di sottoinsiemi chiusa non solo per le operazioni di unione, intersezione e negazione ma anche per la congiunzione di una famiglia numerabile di sottoinsiemi.

S. normato. Uno s. vettoriale si dice normato se per ogni elemento a è definita una funzione (reale non negativa) ∥a∥ detta norma (o lunghezza) di a soddisfacente le condizioni: ∥a∥=0 se e solo se a=0; ∥λa∥=|λ| ∥a∥; ∥a+b∥≤∥a∥+∥b∥. Ogni s. normato diventa uno s. metrico, ove si assuma come distanza di due suoi elementi a, b la norma della loro differenza, cioè ∥a−b∥. Per es., lo s. euclideo Eⁿ delle n-ple (x₁, ..., x_n) è normato con la norma espressa da √‾‾‾‾‾‾x₁²+…‾‾‾‾+x_n²‾‾‾‾ e la distanza di (x₁, ..., x_n) da (y₁, ..., y_n) è

(metrica euclidea). L’applicazione più cospicua della teoria degli s. normati viene fatta nell’analisi funzionale e precisamente nella teoria degli operatori.

S. di probabilità. S. degli eventi misurabile con una funzione probabilità soddisfacente gli assiomi di normalizzazione e finita additività (➔ probabilità).

S. proiettivo. Elementarmente si può dire che uno s. proiettivo di dimensione n si ottiene da uno s. euclideo della stessa dimensione aggiungendo a esso i punti, le rette, ... impropri (o all’infinito) e trattandoli alla stessa stregua degli elementi propri (al finito). In conseguenza, in uno s. proiettivo non è possibile parlare di distanze o altre proprietà metriche (come accade nello s. euclideo) e neppure di parallelismo (come in uno s. affine) ma sostanzialmente solo di proprietà di incidenza. La definizione precisa si può dare, nel caso di uno s. proiettivo reale, per via assiomatica, assegnando i postulati di appartenenza, di ordine e di continuità, ovvero, nel caso di uno s. proiettivo sopra un corpo K, per via analitica. Secondo la definizione analitica, fissato un corpo K (finito o no, non necessariamente commutativo), si chiama s. proiettivo a n dimensioni su K ogni insieme S di elementi (detti punti) che abbia le proprietà: a) esiste una corrispondenza biunivoca tra i punti ξ di S e le (n+1)-ple non nulle (x0, x1, ..., xn) di elementi di K definite a meno di un fattore di proporzionalità (le x0, ..., xn si chiamano coordinate proiettive omogenee del punto ξ); b) un sottospazio di S è un qualunque sottoinsieme S′ i cui punti si ottengono come combinazioni lineari di k punti fissati ξ1, ..., ξk di S, cioè

essendo x_i¹, ..., x_i^k, le coordinate dei punti ξ¹, ..., ξ^k, e c₁, ..., c_k elementi arbitrari di K. Si tratta evidentemente di una generalizzazione della nozione di piano o di s. proiettivo a tre dimensioni nei quali si svolge l’ordinaria geometria proiettiva. Se K non è commutativo, è possibile definire uno s. proiettivo destro o sinistro consentendo che il fattore di proporzionalità delle coordinate e i moltiplicatori c₁, ..., c_k di cui sopra moltiplichino a destra o a sinistra le coordinate x₀, ..., x_n.

S. di Sobolev. Particolare tipo di s. funzionale, che si indica con W^k,p(Ω); si tratta di uno s. di funzioni a valori complessi, definite in un aperto Ω di R^m e tali che: a) possiedono derivate (nel senso delle distribuzioni) fino all’ordine k; b) le derivate appartengono a L^p(Ω), vale a dire che la potenza p-esima del loro modulo è integrabile in Ω.

S. subordinato (o sottospazio). Dato uno s. (topologico, euclideo ecc.) un suo sottoinsieme si dice s. subordinato o sottospazio se la struttura dello s. ambiente subordina su tale sottoinsieme una struttura che lo renda uno s. dello stesso tipo di quello ambiente. Così, per es., un piano dello s. euclideo a tre dimensioni è un sottospazio di quest’ultimo; lo s. delle funzioni derivabili è un sottospazio dello s. delle funzioni continue ecc.

S. topologico. S. costituito da un insieme S di elementi (detti punti dello s.) nel quale sia assegnata una famiglia ℱ di sottoinsiemi (detti insiemi aperti o semplicemente aperti di S) soddisfacenti i seguenti postulati: a) S e l’insieme vuoto appartengono a ℱ; b) ogni unione di elementi di ℱ appartiene a ℱ; c) l’intersezione di ogni famiglia finita di elementi di ℱ appartiene a ℱ. In tali condizioni si dice anche che nell’insieme S è stata introdotta una topologia o una struttura topologica. L’ordinario s. euclideo è uno s. topologico nel quale gli aperti soddisfacenti le a), b), c) sono gli ordinari insiemi aperti; nel caso generale sono invece le a), b), c) stesse assunte come postulati, che conferiscono il carattere di insieme aperto agli elementi della famiglia ℱ. Gli aperti contenenti un dato punto P dello s. (e più in generale gli insiemi che contengono uno di tali aperti) vengono allora assunti come intorni del punto stesso, e un punto Q è da ritenere ‘vicino’ a P se appartiene a un intorno di P. In modo analogo sono definiti gli intorni di un sottoinsieme dello spazio. Per base di uno s. topologico S si intende una famiglia B di aperti non vuoti di S tali che ogni aperto di S sia unione di elementi di B. Se in S esiste una base numerabile, si dice che S è uno s. a base numerabile.

Un’operazione generale, che prende il nome di prodotto topologico, consente di associare a due dati s. topologici S ed S′ un nuovo s. topologico detto il prodotto topologico di S per S′. Esso è lo s. topologico formato dall’insieme S×S′ (prodotto cartesiano di S per S′), nel quale una base di aperti è costituita dai prodotti di coppie di aperti A×A′ (con A⊂S e A′⊂S′).

Una funzione continua tra due s. topologici S ed S′ è una funzione f:S→S′ con la proprietà che la controimmagine di ogni aperto di S′ è un aperto di S (la nozione elementare di funzione continua rientra in questa più generale). Una funzione di S in S′ che sia suriettiva e biunivoca, e che sia continua nei due sensi (biunivoca e bicontinua), prende il nome di omeomorfismo, e due s. topologici S ed S′ si considerano equivalenti, aventi cioè le stesse proprietà topologiche, quando sono omeomorfi, quando cioè esiste un omeomorfismo tra S ed S′.

Accanto alla nozione di intorno ricordiamo anche quella di insieme chiuso di uno s. topologico S come complementare di un insieme aperto, e di chiusura di un sottoinsieme A come intersezione di tutti gli insiemi chiusi contenenti A: la chiusura di A si indica con Ā. Alla stessa nozione di s. topologico si perviene anche assegnando per ogni punto dello s. i sottoinsiemi che debbono intendersi come suoi ‘intorni’ soddisfacenti convenienti postulati (s. di intorni), oppure assegnando per ogni sottoinsieme A dello s. la sua ‘chiusura’ Ā, sempre in modo che siano soddisfatti degli assiomi ben determinati, detti assiomi di Kuratowski (questi sono: A⊂Ā, ∅= ∅−−, A⁼=Ā, A⋂B−−−−=Ā⋂B̄).

Alcune classi notevoli di s. topologici godono di proprietà aggiuntive rispetto a quelle generali derivanti da a), b), c). Una prima classe si ottiene aggiungendo gli assiomi di ‘separazione’; un esempio è dato dagli s. di Hausdorff o s. separati: uno s. topologico è di Hausdorff se per ogni coppia di punti distinti x, y esistono un intorno U di x e uno V di y tra loro disgiunti. Un assioma di separazione più debole che definisce lo s. T₀ di Kolmogorov è: per ogni coppia di punti distinti x, y di S esiste un aperto di x che non contiene y e un aperto di y che non contiene x. Un altro assioma è: per ogni coppia di punti distinti x, y di S esiste un intorno di x che non contiene y e un intorno di y che non contiene x (senza che necessariamente i due intorni siano disgiunti); uno s. topologico che soddisfi tale proprietà si chiama uno s. T₁ (con la stessa terminologia uno s. di Hausdorff si chiama anche s. T₂). Un’altra classe notevole è quella degli s. metrici. In uno s. metrico in cui è definita una distanza tra punti è possibile definire gli intorni di ogni punto e quindi rendere lo s. uno s. di intorni e quindi uno s. topologico. Vale anzi il teorema: ogni s. metrico è uno s. di Hausdorff.

In particolari casi uno s. topologico assume qualifiche e denominazioni speciali; tra le tante ricordiamo: a) connesso, se non è unione di due aperti A, B non vuoti e disgiunti; b) compatto, se ogni ricoprimento dello s. topologico S mediante insiemi aperti contiene una famiglia finita che è ancora un ricoprimento di S; se il ricoprimento è numerabile lo s. si dice di Lindelöf; c) localmente compatto o talvolta paracompatto se ogni punto dello s. ammette un intorno compatto; d) regolare (o T₃) se esso è uno s. T₁ e inoltre comunque si prendano un sottoinsieme chiuso C e un punto x non appartenente a C esistano un intorno di C e un intorno di x tra loro disgiunti; e) normale (o T₄) se esso è uno s. T₁ e se due chiusi disgiunti qualsiasi dello s. hanno due intorni disgiunti; f) completamente regolare (o di Tichonov) se lo s. S è innanzitutto T₁ e inoltre per ogni sottoinsieme chiuso C e ogni punto x non appartenente a C, esiste una funzione continua f di S nell’intervallo [0,1] tale che f(x)=0, f(C)=1; g) separabile (da non confondere con separato) se contiene un insieme numerabile e denso (un sottoinsieme D di S si dice denso se D̄=S).

S. vettoriale. Con riferimento a un campo K (reale, complesso o anche più generale), un insieme V di elementi, detti vettori, si dice s. vettoriale su K se: a) tra gli elementi di V è definita una somma rispetto alla quale V è un ‘modulo’; la somma è cioè associativa e commutativa, esiste l’elemento neutro 0 (vettore nullo) ed esiste l’opposto −v di un elemento qualunque v; b) inoltre è definito il prodotto di un elemento k di K per un vettore v di V, il risultato essendo un vettore kv di V, in modo tale che vengano rispettate certe regole di calcolo del tipo: 1∙v = v; k₁(k₂v) = (k₁k₂)v; (k₁ + k₂)v = k₁v + k₂v; k(v₁ + v₂)=kv₁+kv₂. Se K non è un campo (commutativo) ma un corpo (non necessariamente commutativo) è possibile definire in modo analogo uno s. vettoriale destro e uno s. vettoriale sinistro.

I vettori liberi della meccanica formano uno s. vettoriale rispetto al corpo reale R; i numeri complessi a+ib formano anch’essi uno s. vettoriale reale; analogamente le n-ple ordinate (x₁, ..., x_n) di numeri reali, se si definiscono in modo naturale la somma (x₁, ..., x_n)+(y₁, ..., y_n)=(x₁+y₁, ..., x_n+y_n) e il prodotto per un numero reale r come r(x₁, ..., x_n)=(rx₁, ..., rx_n) (quest’ultimo s. vettoriale si indica con Rⁿ); le funzioni reali di variabile reale definite nell’intervallo (0,1) ecc. Come conseguenza della definizione, è possibile parlare, in uno s. vettoriale, di combinazione lineare di più elementi k₁v₁+ ... +k_rv_r, nonché, di dipendenza e indipendenza lineare: v₁, ..., v_r sono indipendenti se k₁v₁+ ... +k_rv_r=0 solo quando k₁= ... =k_r=0. Sottospazio V′ di V è l’insieme degli elementi di V ottenuto partendo da un sottoinsieme M⊂V e formando tutte le combinazioni lineari a coefficienti in K di elementi di M. Un sottoinsieme B⊂V si dice che costituisce una base per V quando ogni vettore v è esprimibile in modo unico come combinazione lineare di un numero finito di elementi di B. Se la base B è un insieme finito n si dice che V ha dimensione n, altrimenti V ha dimensione infinita. Per es., ha dimensione n lo s. vettoriale delle n-ple (x₁, ..., x_n), una base essendo formata dagli n vettori indipendenti: (1, 0, ... 0), (0, 1, ... 0), ..., (0, 0, ... 1). Sia V uno s. vettoriale su K; si verifica che le forme lineari definite in V, e a valori in K, cioè le funzioni f:V→K tali che f(k₁v₁+k₂v₂)=k₁f(v₁) + k₂f(v₂), formano a loro volta uno s. vettoriale V* detto lo s. duale di V; se V ha dimensione finita n, anche V* ha la stessa dimensione n.

Dati due s. vettoriali qualunque V_n, V_m, di dimensioni rispettive n, m, entrambi su K, il loro prodotto tensoriale, che si indica con V_n⊗V_m, è lo s. vettoriale a nm dimensioni definito come lo s. delle funzioni bilineari definite nel prodotto degli s. duali V_m*×V_n* in K cioè delle funzioni f tali che

La definizione di prodotto tensoriale si può estendere da due a più s. vettoriali. Se in particolare si prendono i fattori del prodotto uguali a uno stesso s. vettoriale V o al suo duale, gli elementi del prodotto tensoriale si chiamano tensori affini su V.

Uno s. vettoriale può essere dotato di strutture o proprietà addizionali che ne particolarizzano la collocazione tra tutti gli s. vettoriali. Una proprietà addizionale che s’incontra frequentemente è l’esistenza del prodotto interno (o prodotto scalare). Si tratta di una funzione V×V→K definita per le coppie di elementi di V e a valori in K, che si indica con (v1, v2) (oppure con v1∙v2) e gode delle seguenti proprietà: (v1, v2)=(v2, v1); (k1v1+k2v2, v3)=k1(v1, v3)+k2(v2, v3). Uno s. vettoriale dotato di prodotto interno si chiama anche uno s. vettoriale euclideo; se inoltre vale la proprietà (v, v)>0 se e solo se v≠0 lo si chiama propriamente euclideo. In uno s. propriamente euclideo si può definire la norma di un vettore v come ∥ν∥ = √‾‾‾‾‾(ν,ν) (uno s. vettoriale propriamente euclideo è uno s. normato; ha senso considerare la disuguaglianza di Schwarz: |(v1,v2)| ≤ |v1|∙|v2|; è inoltre possibile definire l’angolo ϑ di due vettori v1, v2, mediante la

È possibile parlare di vettori v1, v2 ortogonali quando (v1, v2)=0, di base orto-normale ecc.

Uno s. vettoriale dotato di una topologia di Hausdorff è uno s. vettoriale topologico detto convesso se in ogni punto esiste una base di intorni convessi.

Per s. di Minkowski (o spazio-tempo) ➔ cronotopo.

Medicina

Medicina spaziale Branca della medicina che studia i problemi fisiologici, patologici e psicologici connessi con il volo dell’uomo nello spazio. Il compimento d’imprese astronautiche presuppone lo studio e il superamento di molteplici problemi biologico-medici che, tra l’altro, riguardano: gli effetti esercitati sull’organismo umano dalle variazioni gravitazionali (accelerazione al momento del lancio, decelerazione al rientro, diminuzione o assenza di gravità nelle fasi intermedie); l’igiene personale degli astronauti e dell’abitacolo spaziale (capsula spaziale oppure astronave); l’esigenza di non contaminare lo s. o i corpi extraterrestri; il controllo da terra, a grandi distanze, delle condizioni cliniche dell’equipaggio; l’alimentazione degli astronauti; il mantenimento di un adatto microclima nell’interno dell’astronave; le ripercussioni sulla psiche della navigazione spaziale di lunga durata; il riadattamento psicofisico dopo il rientro a terra.

Vita in ambiente confinato

Il volo spaziale avviene in condizioni fisiche, ambientali e dinamiche particolari, alcune delle quali incompatibili con la vita: la pressione ambientale è praticamente nulla, l’atmosfera è costituita da rari ioni dei gas terrestri nella fascia meno lontana (ionosfera) e da corpuscoli della radiazione solare e cosmica al di sopra di questa; la temperatura può essere elevatissima su un corpo esposto alla radiazione solare, o estremamente bassa se il corpo è schermato da questa. Per tali motivi, la vita è possibile solo in una cabina a tenuta di gas, climatizzata, contenente aria continuamente rigenerata e scorte di acqua e alimenti.

Anche se un grande progresso si è registrato dalle prime capsule degli anni 1960, che avevano volumi utili intorno al metro cubo per membro di equipaggio, tuttavia le dimensioni interne di veicoli e stazioni spaziali sono tuttora assai limitate. L’atmosfera artificiale è costituita da circa il 21% di O2 in azoto, alla pressione atmosferica; essa è fatta circolare, filtrata e depurata continuamente e rigenerata con l’O2 delle scorte. La costanza della temperatura (che oscilla fra 20 e 25 °C) è ottenuta disperdendo il calore prodotto dall’equipaggio e dalle apparecchiature all’esterno mediante scambiatori di calore, che lo irraggiano verso il lato in ombra del veicolo. La relativa costanza del microclima è tenuta sotto controllo e assicurata da automatismi. Le scorte sono di regola rinnovate, nel caso di lunghe missioni, per mezzo di navette periodicamente inviate. Sono in continuo miglioramento il comfort ambientale (anche sul piano psicologico), la disponibilità di servizi igienici personali, l’alimentazione, la possibilità di fruire di privacy, seppure ridotta, e di comunicare con la famiglia e con gli psicologi che curano l’assistenza specialistica dell’equipaggio. Sono stati descritti episodi di irritabilità, di intolleranza, di ansia non giustificata nei rapporti interpersonali con gli altri membri dell’equipaggio e/o con il personale delle basi. L’analisi dello spettro della voce ha rivelato in qualche caso lievi stati di depressione.

Diverse condizioni, o accidentali o programmate, possono richiedere l’uscita di membri dell’equipaggio dal veicolo in volo e la permanenza nello s. per diverse ore. Questa attività extraveicolare (EVA) si può svolgere grazie all’utilizzo di robusti scafandri multistrato, impermeabili ai gas, contenenti O2 al 30% in N2, climatizzato e depurato in circuito chiuso mediante dispositivi contenuti nello zaino. Lo scafandro è molto rigido e causa difficoltà nei movimenti, fatica, maggior lavoro muscolare e produzione di calore. L’EVA deve essere preceduta da periodi di deazotazione per impedire la comparsa di embolismo gassoso.

Microgravità

Denominata anche assenza di peso, è la condizione peculiare che si verifica nei veicoli spaziale orbitanti, nella quale la forza di gravità terrestre è equilibrata dalla forza centrifuga. I viventi non possiedono adattamenti naturali alla microgravità; dispongono però di propriocettori generali, soprattutto nell’apparato locomotore, e speciali (vestibolo dell’orecchio interno), sensibili alle accelerazioni lineari e angolari, i quali intervengono nella regolazione della postura e dell’equilibrio, nel tono della muscolatura scheletrica e nella motricità volontaria. L’assenza di gravità provoca spostamento dei liquidi corporei (dalla metà podalica a quella cefalica), mentre la riduzione del carico su scheletro e muscoli ne determina demineralizzazione e rispettivamente ipodinamia e ipotrofia. Anche a livello cellulare avvengono fenomeni fisico-chimici di cui non sono stati finora dimostrati gli eventuali effetti su tutto l’organismo.

L’apparato vestibolare ha una parte (organo otolitico) molto sensibile alle accelerazioni lineari (come la gravità terrestre) e una (le ampolle dei 3 canali semicircolari) sensibile più specificamente alle accelerazioni angolari (per es., nella rotazione del capo). La microgravità altera le risposte dell’organo otolitico, ma non influenza manifestamente quelle dei recettori ampollari. Si può generare, pertanto, un disaccordo sensoriale intravestibolare, complicato e aggravato dal conflitto tra le informazioni provenienti da questo apparato e quelle visive, propriocettive, viscerali e cutanee, che causa il cosiddetto mal di spazio. Questa sindrome si manifesta, in modo più o meno grave, nella maggioranza degli astronauti nei primi 2-3 giorni del volo; in seguito si attenua, spontaneamente e/o con l’uso di farmaci antichinetosici. Una parziale profilassi si ottiene con tecniche di addestramento al suolo e con l’uso di farmaci contenenti prometazina, efedrina, destroamfetamina, dimenidridato, scopolammina.

La funzione respiratoria polmonare è moderatamente influenzata: la capacità vitale diminuisce anche del 25% nei lunghi voli, a causa del sollevamento medio della posizione del diaframma e del maggior contenuto di sangue nei capillari. La circolazione del sangue viene alterata dalla scomparsa dei fenomeni idrostatici, alla quale consegue lo spostamento di notevoli quantità di liquido (sangue, poi il liquido interstiziale e la linfa) verso il capo, il collo e i polmoni, a spese di quello contenuto nel bacino e negli arti inferiori. Il volume spostato è intorno a 3-4 litri e il fenomeno è rivelato da modificazioni dell’aspetto (volto e collo turgidi, palpebre ispessite, lieve protrusione dei bulbi oculari, vene giugulari e superficiali distese, arti inferiori assottigliati), da variazioni nelle misure del perimetro della coscia e della gamba e, come si è detto, della capacità vitale.

Nel corso dei primi giorni di volo, per effetto dei riflessi che partono da vari recettori di pressione vascolare (seno carotideo), cardiaci (atriali) e polmonari, si instaurano alcuni fenomeni di compenso, quali l’aumento della diuresi e/o la diminuzione del bisogno di bere, che finiscono per portare a una perdita di 2-4 kg di liquidi. Anche la gettata cardiaca subisce piccole variazioni intorno al valore fisiologico di riposo al suolo, legate essenzialmente all’andamento della frequenza. Il volume delle cavità ventricolari e la massa totale del cuore diminuiscono del 10-15% nei voli di lunga durata, verosimilmente per la diminuzione del lavoro a causa della scomparsa della pressione idrostatica. Lo svolgimento di un programma di vigoroso esercizio fisico, specialmente nelle settimane che precedono il rientro, l’uso regolare di speciali dispositivi che in volo provocano modificazioni circolatorie simili a quelle causate dall’ortostatismo (➔ ortostatico) e l’assunzione di fluorocortisone acetato e/o di soluzioni saline nei 2-3 giorni finali attenuano notevolmente questi fenomeni i quali, peraltro, non sembrano tali da costringere a limitare la durata del volo. Subito dopo il ritorno al suolo l’uso degli indumenti antigravità evita i disturbi dell’intolleranza ortostatica.

L’assenza di peso provoca la cessazione del carico fisiologico sulle ossa. A ciò conseguono demineralizzazione, minore attività degli osteoblasti, aumento del Ca11 nel sangue e della sua eliminazione intestinale e renale. Sono presenti anche anomalie strutturali delle ossa portanti simili a quelle dell’osteoporosi senile o a quelle causate da lunga immobilità. Il fenomeno appare confinato alle ossa pelviche, alle vertebre lombari e al femore, mentre aumenta il contenuto minerale del cranio e della gabbia toracica. La calcemia elevata inibisce la secrezione di ormone paratiroideo e talvolta della tirocalcitonina, con influenza negativa sull’attivazione della provitamina D e, conseguentemente, sull’assorbimento del Ca11, per cui il bilancio di questo elemento diviene negativo dopo pochi giorni di volo. L’assunzione di difosfonati ha un relativo effetto protettivo.

I muscoli scheletrici con funzione antigravitativa (responsabili della stazione eretta e, in parte, della deambulazione) presentano una modica ipotrofia e la forza e la resistenza della contrazione diminuiscono del 10-30%. Aumentano i processi catabolici e il bilancio azotato diviene negativo, a spese soprattutto di quel tipo di fibre, a contrazione lenta, che prevalgono nei muscoli ad attività statica. Nei voli di durata medio-lunga quasi tutti gli equipaggi presentano una diminuzione del 10-20% del numero totale degli eritrociti (e maggiormente dei reticolociti) e lievi alterazioni morfologiche, sembra per ridotta attività eritropoietinica, ma senza disturbi manifesti. Importanti sono la linfocitopenia spontanea e la diminuzione della sensibilità di queste cellule in coltura all’azione di agenti mitogeni, cioè che favoriscono la moltiplicazione. Ciò ha evidenti implicazioni in campo immunologico. Anche la risposta immunitaria sembra alquanto depressa. La funzione endocrina non presenta modificazioni specifiche attribuibili con certezza alla microgravità. Lo stress conseguente alle intense sollecitazioni psicofisiologiche nel periodo preparatorio e in quello del volo è sicuramente responsabile delle variazioni di cortisolo, catecolammine, ormone dell’accrescimento, prolattina e altri ormoni, descritte episodicamente.

La riproduzione, anche di piccoli Mammiferi, è possibile durante il volo spaziale: qualche anomalia nei feti, come pure il ritardato accrescimento dei neonati, sono probabilmente in rapporto alla reazione di stress subita dall’animale e, in qualche caso, al maggior assorbimento di radiazioni ionizzanti.

Effetti delle radiazioni cosmiche

I viventi sul nostro pianeta sono protetti dalle radiazioni (elettromagnetiche o di altra natura) di origine solare e cosmica, grazie a due diversi schermi. Quello esterno è rappresentato dalle fasce di van Allen, dove le particelle cariche sono trattenute dal campo magnetico terrestre e si muovono a spirale lungo le sue linee di forza (solo in parte riescono ad attraversarlo, specialmente nelle regioni polari). Lo schermo interno è l’atmosfera, che in parte riflette (ionosfera) e in parte blocca o degrada le radiazioni. Questa seconda protezione manca nel volo orbitale e ambedue sono assenti nei viaggi verso gli altri corpi celesti. Per es., mentre nei voli dello Space Shuttle la dose media giornaliera di radiazioni assorbita oscilla fra 5 e 10 mrad, durante la missione lunare dell’Apollo 14 sono stati superati i 127 mrad/giorno. Nel primo caso si superano di poco, e nel secondo di molto, i limiti stabiliti dal National council of radiation protection. Una condizione particolare è l’EVA, in cui manca anche la piccola protezione delle pareti del veicolo. Poiché le radiazioni ionizzanti provocano la formazione di radicali liberi e di perossidi, cioè di agenti ossidanti molto aggressivi, si è tentato di neutralizzarli con diversi composti, quali la coppia cistina-cisteina, il glutatione e l’ubichinone ridotti, la vitamina E e altri antiossidanti. Le radiazioni ultravioletta e infrarossa non presentano problemi purché l’organismo sia schermato dall’azione diretta (l’UV è particolarmente dannosa per gli occhi).

Prospettive dell’esplorazione umana nel cosmo

Per voli di lunga durata, specialmente se all’esterno delle fasce di van Allen (per es., Terra-Marte e ritorno), si ritiene che i limiti possano essere posti da almeno tre condizioni: superamento della dose non dannosa di radiazioni ionizzanti assorbite, demineralizzazione progressiva dello scheletro e perdita delle difese immunitarie. A queste si deve aggiungere la possibilità di un danno progressivo degli organi emolinfopoietici e dei sistemi di regolazione posturale della circolazione, tale che il decondizionamento cardiovascolare (funzionale-reversibile) porti ad alterazioni organiche irreversibili con impossibilità di riadattamento, anche psicologico, alla vita terrestre. Da non trascurare, infine, le eventuali mutazioni patogene di microrganismi, di colture vegetali o di allevamenti destinati alla nutrizione. Un pericolo reale è rappresentato dall’urto di micrometeoriti che viaggiano a 30-50 km al secondo e attraversano le pareti del veicolo e ancor più quelle degli scafandri spaziali.

Politologia

S. vitale Traduzione corrente del tedesco Lebensraum, con la quale si indica l’estensione territoriale indispensabile, secondo la visione della scuola geopolitica tedesca ripresa dal nazionalsocialismo, affinché un popolo e uno Stato possano avere le necessarie risorse e possibilità economiche di vita e di sviluppo, e quindi le necessarie garanzie di autonomia e di sicurezza. La formula è stata resa celebre da A. Hit;ler nella sua opera programmatica Mein Kampf e posta a fondamento della sua politica espansionistica.

Psicologia

Il problema della percezione dello s. è stato uno dei temi di ricerca più rilevanti della psicologia fin dal suo costituirsi in disciplina scientifica autonoma. Basti citare le notissime ricerche di E. Hering (1861) e di H.L.F. von Helmholtz (1867) sullo s. visivo e quelle di inizio Novecento (1902) di B.B. Bourdon (1860-1943) e di W. Wundt (1908 e 1911). Particolarmente studiati, per quanto riguarda la percezione visiva, il fenomeno dell’unificazione delle due immagini retiniche, l’acutezza stereoscopica (misura della soglia percettibile della parallasse stereoscopica basata sull’esistenza di una disparità retinica), l’acutezza visiva e l’organizzazione dello s. visivo del piano. Particolare rilievo è stato dato alla percezione visiva della distanza in profondità, alla percezione delle dimensioni e al complesso problema del rapporto dimensione-distanza. Le percezioni spaziali uditive risultano assai meno accurate di quelle visive e tuttavia permettono, in base alla parallasse biauricolare, di cogliere la direzione di un suono e le sue distanze. Ancor meno precise delle altre percezioni spaziali sono quelle di tipo tattile-cinestesico (percezione dello spostamento del proprio corpo, dell’ampiezza di un movimento, valutazione della distanza in base a dati propriocettivi, schema corporeo ecc.). Di notevole interesse gli studi di H.A. Witkin (1949) sulla percezione della verticale, che hanno permesso di mettere a confronto l’apporto di dati diversi, talvolta conflittuali, nella costruzione dello s. percettivo, approdando a formulare l’ipotesi di una connessione tra le modalità percettive preferenziali del singolo soggetto e le sue caratteristiche di personalità (ipotesi della campo-dipendenza). Una teoria generale di vasta portata sulla percezione spaziale è inoltre quella sensorio-teorica di H. Werner e S. Wapner (1952). L’indagine sull’evoluzione genetica della percezione spaziale (J. Piaget, 1950) ha messo in luce dapprima la coesistenza indifferenziata dei vari tipi di s. nel bambino (0-4 mesi), quindi l’inizio della coordinazione fra i diversi dati sensoriali (4-9 mesi) e infine (a 18 mesi) la costruzione di uno s. sensorio-motorio coerente. La rappresentazione dello s., invece, non si costituirebbe fino agli 11-12 anni.