unità
Biologia
In biologia molecolare, u. trascrizionale, la distanza fra i siti di inizio e di terminazione riconosciuti dalla RNA polimerasi (➔ trascrizione); può includere più di un gene. In genetica, u. di mappa, la distanza fra due geni associati.
Economia
U. di prezzo Nella pratica commerciale e mercantile, il prezzo riferito a tutta la partita di merce venduta nel suo complesso (o anche ad altri parametri particolari). U. di contratto La misura unitaria o complessiva dell’obbligazione delle parti contraenti, costante e uniforme nell’ambito di determinati regolamenti di borsa. U. di nolo Nei trasporti marittimi, la misura unitaria del nolo riferita a un’u. di massa, o di volume o di collo, della merce da trasportare. U. lavorativa o di lavoro Ciascuna u. di tempo (calcolabile in ore, giornate ecc., a seconda delle esigenze) sulla base della quale si suddivide l’attività di un lavoratore, o di un’azienda, utilizzata allo scopo di poterla programmare e controllare più agevolmente; nelle statistiche economiche u. di lavoro è l’equivalente a tempo pieno di posizioni lavorative. U. monetaria È la moneta base di un sistema monetario internazionale (➔ sistema), mentre l’u. di conto è l’unità monetaria fittizia utilizzata per operazioni di pagamento o prestiti internazionali (per l’u. di conto europea, ➔ ECU).
Nei contratti di utenza telefonica, si chiama u. (comunemente anche scatto) ogni periodo di un determinato numero di minuti o di secondi, indivisibile, cui corrisponde un’u. tariffaria.
Farmaceutica
U. biologica U. di misura riferita all’effetto biologico di una determinata sostanza. Il suo impiego ha consentito la titolazione di prodotti che in passato non erano suscettibili di misure ponderali (sieri, certi ormoni e vitamine). Si denomina dall’animale usato nella sperimentazione (u. cavia, u. rana ecc.), o dall’ideatore del metodo di dosaggio (u. Collip ecc.), o anche dall’azione farmacodinamica (u. ossitocica, u. antidiuretica ecc.); per i prodotti di più largo impiego si usa un’u. internazionale (UI), stabilita in base a campionamento regolato dall’Organizzazione mondiale della sanità. Quando è possibile, si tende a sostituire tali u. con u. di massa (μm, ng, pg).
Fisica
U. di misura Con riferimento a una determinata classe di grandezze fisiche della stessa specie, la grandezza di quella specie (per le lunghezze, per es., il metro) assunta come campione e termine di confronto per la misurazione di tutte le grandezze della classe.
Generalità
L’u. di misura si sceglie arbitrariamente soltanto per alcune grandezze, dette perciò fondamentali o primitive o primarie o di base, e si esprimono in funzione di esse le u. di tutte le altre grandezze, dette derivate. A tal fine, di ogni grandezza derivata si dà la definizione dimensionale in funzione delle grandezze assunte come fondamentali (per es., in cinematica, assunte come tali lunghezza e tempo, la velocità si definisce come rapporto fra lunghezza e tempo), quindi si scrive il prodotto delle prescelte u. fondamentali attribuendo a ognuna di esse come esponente la dimensione con cui la corrispondente grandezza fondamentale interviene nella definizione dimensionale della grandezza in esame (per es., assunte come u. di lunghezza e di tempo il metro e il secondo, è u. di misura della velocità il m∙s−1). Le grandezze fondamentali devono essere fra loro indipendenti, nel senso che l’u. di una di esse non sia ricavabile dalle altre (per es., lunghezza e area non sono fra loro indipendenti mentre lo sono lunghezza e tempo); devono essere tali, per numero e natura, da consentire la definizione di tutte le grandezze derivate (il numero, in particolare, è dato dalla differenza fra il numero di grandezze considerate e il numero di relazioni fra le grandezze stesse). Ciascuna di esse deve poi permettere la scelta di un’u. rappresentabile mediante un campione facilmente riproducibile e possibilmente materializzabile in un oggetto o strumento, per quanto possibile, semplice e invariabile. I campioni delle u. di misura fondamentali di un sistema, definiti operativamente, debbono dunque essere indipendenti, invarianti, riproducibili, precisi e accessibili. Quando, soddisfatte queste condizioni, si convenga di misurare tutte le grandezze di una stessa specie con la stessa u. (per es., tutte le lunghezze in metri), si viene a costituire un sistema di u. di misura (➔ sistema).
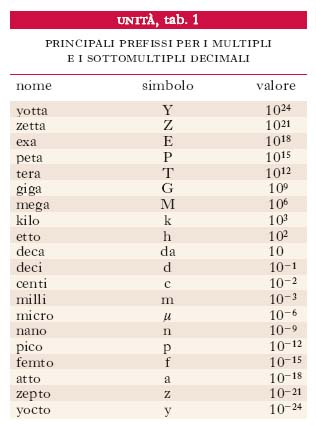
Fissata che sia una u., per evitare calcoli con numeri troppo grandi o troppo piccoli può convenire l’uso di multipli o sottomultipli, decimali o no, a seconda dei casi. Multipli e sottomultipli decimali, espressi abitualmente mediante potenze di 10, hanno in genere il nome che risulta dalla giustapposizione di un prefisso al nome dell’u. (tab. 1). Va sotto il nome di sistema metrico decimale, o semplicemente sistema metrico, il complesso di tutte le u. di misura i cui multipli e sottomultipli sono decimali.
U. di misura di lunghezze, aree, volumi, angoli
Nell’ambito della geometria le grandezze suscettibili di definizione quantitativa e quindi di misurazione sono: le lunghezze, le aree, i volumi, gli angoli piani, gli angoli solidi. Assunta come fondamentale la lunghezza, e come u. di lunghezza il metro, u. di area e di volume sono rispettivamente il m2 e il m3. La misura di un angolo piano si definisce mediante una relazione del tipo ϕ=ks/r, dove k è un fattore numerico, r il raggio di una circonferenza c con centro nel vertice dell’angolo, s l’arco di c sotteso dall’angolo. Gli angoli piani si presentano quindi come grandezze adimensionate e adimensionata è pure la loro unità. Questa varia, naturalmente, a seconda del valore che si attribuisce a k: per k=1 è u. il radiante, angolo che sottende un arco di circonferenza di lunghezza pari al raggio (si tratta dell’unica u. coerente per gli usi della fisica); per k=360/2π si ha il grado sessagesimale o nonagesimale o babilonese, pari alla 360ª parte dell’angolo giro, avente come sottomultipli il primo sessagesimale, 60ª parte del grado, e il secondo sessagesimale, 60ª parte del primo; per k=400/2π si ha il grado centesimale, pari alla 400ª parte dell’angolo giro, avente come sottomultipli il primo centesimale (100ª parte del grado) e il secondo centesimale (100ª parte del primo). Per gli angoli solidi l’u. di misura abituale è lo steradiante.
A ogni multiplo o sottomultiplo del metro corrisponde un multiplo o sottomultiplo del metro quadrato e del metro cubo. Se il rapporto fra l’u. di lunghezza e un suo multiplo o sottomultiplo è 10n, il rapporto fra l’u. di area e il corrispondente multiplo o sottomultiplo è 102n e quello fra l’u. di volume e il corrispondente multiplo o sottomultiplo è 103n: così, per es., essendo il decimetro la decima parte del metro (1 dm=10–1 m), il decimetro quadrato è la centesima parte del metro quadrato (1 dm2=10–2 m2), il decimetro cubo è la millesima parte del metro cubo (1 dm3=10–3 m3).
Accanto alle u. di area ora ricordate, definite con diretto riferimento al metro, è molto usata, in agrimensura, l’ara (a, 102 m2) con il suo multiplo ettaro (ha, 104 m2) e il sottomultiplo centiara (ca, 10−2 m2). Accanto al metro cubo con i suoi multipli e sottomultipli, sono anche usate per misure di volume di liquidi le u. di capacità: il litro, che si identifica con il decimetro cubo, e i suoi multipli e sottomultipli.
Sistemi di u. nei vari campi della fisica
In fisica, oltre alle u. geometriche, si introducono a seconda del settore al quale il sistema è destinato: u. meccaniche, u. termologiche e u. elettromagnetiche; e inoltre u. fotometriche (➔ fotometria) e u. speciali, come anno-luce, parsec, elettronvolt ecc.
U. meccaniche In cinematica, alla lunghezza si associa come grandezza fondamentale il tempo; e al metro si affianca, come u. fondamentale, per es., il secondo. Le principali u. cinematiche nel sistema m, s sono: u. di velocità (m ∙ s−1), u. di velocità angolare (rad ∙ s−1), u. di accelerazione (m ∙ s−2), u. di accelerazione angolare (rad ∙ s−2), u. di frequenza (s−1 hertz), u. di portata in volume (m3 ∙ s−1).
Il passaggio dalla cinematica alla dinamica è segnato dalla comparsa di due nuove grandezze, forza e massa, legate fra loro dalla relazione fondamentale della dinamica F = ma, le cui u. non possono essere ricondotte a lunghezza e tempo. Così, accanto alle u. di lunghezza e di tempo deve entrare nel gruppo delle u. fondamentali l’u. di una delle due nuove grandezze. Se si assume la massa come grandezza fondamentale, la forza assume il ruolo di grandezza derivata, e viceversa. I sistemi di u. nei quali sono grandezze fondamentali lunghezza, massa, tempo sono, per il carattere invariantivo della massa, sistemi assoluti; quelli nei quali sono grandezze fondamentali lunghezza, forza e tempo sono detti sistemi tecnici, o pratici. È sistema assoluto il sistema MKS, in cui u. di lunghezza è il metro, di massa il kilogrammo (kg; ➔ kilo-), di tempo il secondo; ed è sistema assoluto il sistema CGS (centimetro, grammo, secondo).
U. termologiche. Per costituire un sistema di u. di misura che copra tutte le esigenze della termologia occorre e basta associare, come fondamentale, alle grandezze meccaniche fondamentali una quarta grandezza opportunamente scelta. Come tale è ormai abituale assumere la temperatura termodinamica T e associare questa alle grandezze di un sistema meccanico assoluto, così che le 4 grandezze fondamentali della termologia vengono a essere: lunghezza (l), massa (m), tempo (t), temperatura termodinamica (T). Generalmente il sistema di u. meccaniche di partenza è il sistema MKS, l’u. di temperatura è il kelvin (simbolo K). Si costituisce così il sistema MKSK.
Sistemi di u. nell’elettromagnetismo. Un sistema di u. in grado di fornire un’u. di misura per ciascuna delle grandezze che intervengono nell’elettromagnetismo si costituisce associando alle grandezze fondamentali meccaniche una grandezza di natura elettromagnetica. La scelta della grandezza elettromagnetica fondamentale è limitata dall’esigenza di poterne costruire campioni stabili, abbastanza semplici e facilmente riproducibili. Come grandezza fondamentale può essere scelta la costante dielettrica assoluta del vuoto ε0, con la possibilità di attribuirle carattere di grandezza adimensionata e valore arbitrariamente prefissato.
Sistema Internazionale
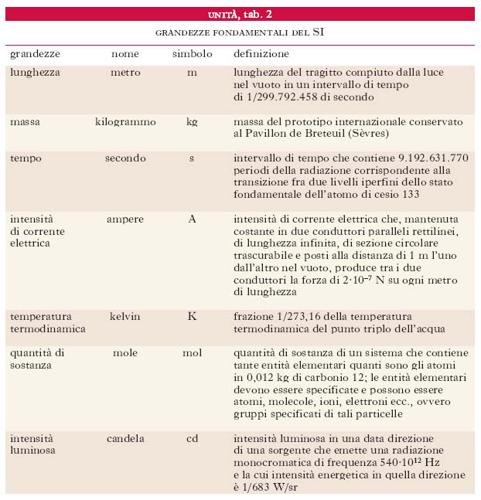
Nel 1875 a Parigi 17 Stati, tra cui l’Italia, mirando all’unificazione mondiale delle misure fisiche, siglarono la Convenzione del metro, alla quale oggi aderiscono 51 paesi. In base a tale convenzione, un comitato tecnico, il CIPM (Comité International des Poids et Mesures), ha il compito di prendere delle risoluzioni sulle unità di misura e sui loro campioni. Le proposte del CIPM sono adottate dalla CGPM (Conférence Générale des Poids et Mesures) e rese esecutive dal Bureau international des poids et mesures (➔). La Convenzione del metro introdusse il Sistema metrico decimale. Da esso discende il Sistema Internazionale (SI), che nel 1960 l’11a CGPM decise dovesse essere adottato per tutte le esigenze metrologiche della scienza e della tecnica e che è considerato quindi il sistema definitivo e unico di u. di misura. Il SI prevede 7 unità fondamentali: metro per la lunghezza, kilogrammo per la massa, secondo per il tempo, ampere per l’intensità di corrente, kelvin per la temperatura, mole per la quantità di sostanza, candela per l’intensità luminosa (tab. 2). Le u. di misura delle grandezze derivate nel SI si ottengono a partire dalle equazioni dimensionali delle grandezze stesse in funzione delle u. fondamentali.
Sistema di u. atomiche
È usato esclusivamente in questioni di fisica atomica, nucleare e subnucleare ed è anche noto, dal nome del fisico che lo propose (1926), come sistema di Hartree; è basato sull’assunzione, come grandezze fondamentali e di valore unitario, dell’u. quantistica h/(2π) con h costante di Planck, della massa di riposo dell’elettrone, m0, e della carica elettrica del protone, e. In tale sistema, non razionalizzato, le varie u. di misura hanno in genere un immediato significato nel campo della fisica atomica. Per es., u. di lunghezza, pari a h2/(4π2m0e2), altro non è che il raggio di Bohr; l’u. di velocità, 4π2e2/h2, è la velocità dell’elettrone nello stato fondamentale dell’atomo di idrogeno; l’u. di numero di onde è la costante di Rydberg dell’idrogeno ecc. In particolare, si chiama u. atomica l’u. di misura dell’energia, 4π2m0e4/h2, che rappresenta l’energia potenziale dell’elettrone dell’atomo di idrogeno nell’orbita fondamentale di Bohr. Una variante del sistema, usata specialmente in questioni di meccanica quantistica relativistica, consiste nell’assumere come grandezze fondamentali il valore unitario h/(2π) e la velocità c delle radiazioni elettromagnetiche nel vuoto (sistema naturale della fisica subnucleare).
Istruzione
U. didattica Sezione o parte di una disciplina di studio, dotata di relativa autonomia e tuttavia correlata all’insieme del programma. Nell’insegnamento tradizionale, centrato sul libro di testo, l’u. didattica ha carattere prevalentemente contenutistico e consiste nello svolgimento di una tematica relativamente compiuta, pressappoco corrispondente a un capitolo del testo adottato. Nelle forme di organizzazione modulare dell’insegnamento, l’u. didattica è più direttamente finalizzata all’apprendimento e comprende, di norma, l’inventario dei prerequisiti richiesti, l’individuazione di un definito nucleo tematico e degli eventuali apporti interdisciplinari, nonché la definizione dei tempi di svolgimento, delle procedure didattiche, delle modalità di verifica dell’apprendimento stesso. Le diverse u., dette perciò anche moduli, devono essere in grado di combinarsi, secondo criteri adeguati (di natura contenutistica, logica o psicopedagogica), in un più organico percorso di studio.
Matematica
In matematica, il numero reale 1, in quanto è il fondamento della numerazione; le u. di un numero sono le cifre da 1 a 9, con in più lo zero, che si scrivono all’estrema destra di un numero intero (o immediatamente prima della virgola se il numero è decimale), nel posto delle unità.
Proprietà dell’u. sono: l’u. è l’elemento indifferente rispetto alla moltiplicazione, cioè se a è un qualunque numero reale, si ha (1∙a=a∙1=a): ne segue perciò che ogni numero intero è multiplo dell’u.; l’inverso di 1 è 1 (1∙1=1), e, più in generale, tutte le potenze dell’u. con esponente positivo o negativo coincidono con l’u. stessa. Si hanno allora varie generalizzazioni del concetto di u., le più importanti delle quali sono: a) in un insieme astratto nel quale sia definita un’operazione di composizione, che si potrà chiamare ‘moltiplicazione’ e indicare con il simbolo della moltiplicazione ordinaria, si chiama elemento u. o brevemente u. un elemento u indifferente rispetto a questa operazione, e cioè tale che: u∙a=a∙u=a qualunque sia l’elemento a dell’insieme. Se poi si ha soltanto u∙a=a (oppure a∙u=a), l’elemento u si chiamerà u. sinistra (rispettivamente u. destra). In un gruppo, vi è una e una sola u., sinistra e destra insieme (u. bilatera o semplicemente u.); in un anello, in un’algebra ecc. può non esservi u.; tuttavia, se vi è una u. bilatera, essa è unica; b) i numeri complessi si dicono numeri a due u. (perché ogni numero complesso si può scrivere nella forma: a∙1+b∙i (dove a, b, sono numeri reali; i=√‾‾‾‾−1 è l’u. immaginaria). Si chiamano in generale sistemi di numeri a n u. (sistemi ipercomplessi, o algebre) quei sistemi algebrici nei quali ogni elemento si può esprimere, in uno e in un sol modo, mediante una combinazione lineare a1u1+a2u2+ ... +anun di n elementi ui (unità), con le ai numeri reali (o complessi o, più in generale, elementi di un dato corpo K); c) matrice u. di ordine n è la matrice che ha nulli tutti gli elementi tranne quelli sulla diagonale principale che sono eguali a 1. Moltiplicando tale matrice per una qualunque altra dello stesso ordine, quest’ultima rimane invariata.
Scienza militare
Nell’esercito di terra, si dicono u. i reparti delle varie armi, nonché i complessi organici formati da più elementi di armi diverse e i raggruppamenti di più complessi: u. minori , i reparti delle varie armi fino al battaglione o equivalenti; grandi u., i raggruppamenti di u. delle varie armi: brigata, divisione, corpo d’armata, armata, gruppo d’armate. Queste a loro volta si distinguono in grandi u. semplici, che sono i raggruppamenti formati da u. semplici delle varie armi (brigata e divisione), e grandi u. complesse, che sono costituite da più grandi u. semplici (corpo d’armata, armata). Si distinguono inoltre in u. tattiche (brigata, divisione e corpo d’armata) e u. strategiche (armata e gruppo d’armata), e anche in u. da combattimento e u. servizi, a seconda che si tratti di reparto addestrato e armato per il combattimento vero e proprio o che disponga di mezzi e attrezzature per compiere servizi di vario genere nel campo di battaglia o nelle immediate retrovie. La fisionomia delle grandi u. è comune agli eserciti di tutto il mondo, quantunque la loro denominazione possa essere diversa.
In Marina, specialmente nella Marina militare, si dice genericamente u. una nave di un determinato tipo. Il termine designa inoltre l’insieme organico di più navi: così la squadra, la divisione, la squadriglia ecc. costituiscono, in ordine decrescente d’importanza, le u. organiche nelle quali è divisa una flotta.
In aeronautica, u. aerea è, in senso stretto, ogni singolo aeromobile militare; in senso lato, l’insieme di più aeromobili militari anche di specialità diverse, organicamente riuniti con personale, materiale e relativo comando.
Statistica
U. statistica L’individuo, l’ente, il caso, o il fatto singolo, che viene rilevato e che si distingue da ogni altro individuo, ente, caso o fatto dell’insieme. Si suole distinguere in semplice, composta, complessa. Semplice è quella non suscettibile di divisione o distinzione, per es., la persona, l’animale, la cosa; composta è quella costituita da più u. semplici della stessa natura, per es., la famiglia, il gregge ecc.; complessa, quella costituita da u. semplici di diversa natura, ovvero anche da u. semplici e unità composte, per es., l’azienda.
Teatro
Legge delle tre u. L’u. di tempo, di luogo, di azione che costituisce la regola della tragedia secondo la dottrina classica.
Aristotele (Poetica V) aveva scritto che la favola della tragedia deve essere compiuta e perfetta, deve cioè avere u.; e che l’azione dell’epopea e quella della tragedia differiscono nella lunghezza, «perché la tragedia fa tutto il possibile per svolgersi in un sol giro di sole o poco più, mentre l’epopea non ha limiti di tempo». Il passo è una semplice deduzione dalla pratica della tragedia greca, ma dai classicisti italiani del Rinascimento, nella loro ricerca di canoni fissi di bellezza, fu interpretato e sviluppato come una vera e propria regola. Fu L. Castelvetro nella sua Poetica (1570) a dar forma definitiva alle tre u., a sancire, cioè, oltre all’unicità dell’azione, quella della scena e la regola che gli avvenimenti rappresentati non potessero avere una durata superiore a 24 ore. Applicata rigorosamente dai tragici classicisti francesi, ma ignorata dagli elisabettiani, la regola restò ferma, eccetto qualche autorevole voce di dissenso, fino al Romanticismo. La definitiva liquidazione della regola delle u. si ebbe in Italia con la prefazione al Conte di Carmagnola e la Lettera a Monsieur Chauvet di A. Manzoni.