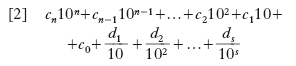numerazione
In matematica, il sistema dei numeri e la loro rappresentazione grafica. Nell’uso comune, il procedimento con cui vengono contraddistinti con numeri i singoli elementi di una successione, e il risultato di tale procedimento
Matematica
Stabilire un sistema di n. significa attribuire dei nomi ai diversi numeri e adottare dei simboli o cifre atti a rappresentarli. Originariamente ci si serviva di una n. strumentale, che si valeva di tacche incise su asticelle di legno, di file o mucchietti di ciottoli, di nodi fatti su cordicelle, cui venivano fatti corrispondere, a uno a uno, gli oggetti da contare; oppure dell’indigitazione, che permetteva di contare facendo corrispondere gli oggetti alle dita della mano ed eseguire anche rapidamente calcoli aritmetici. L’uso dell’indigitazione portò a fissare la cinquina come unità di base, portò cioè al sistema di n. quinario, che sembra sia il più antico sistema di numerazione.
N. scritta e n. parlata
La rappresentazione dei numeri mediante la n. strumentale ha dato luogo alla formazione di opportuni simboli adatti all’indicazione dei numeri. Inizialmente i numeri si rappresentavano mediante ripetizione di un unico simbolo che esprimeva l’unità (n. primitiva). In una fase più evoluta, accanto al simbolo che indicava l’unità ve ne furono altri che designavano raggruppamenti di unità; tali segni (in una sequenza ordinata normalmente a partire dal più grande) esprimevano un qualsiasi numero per lo più mediante la loro somma, come per es. nella n. romana. Un progresso decisivo si è avuto con la n. posizionale, iniziata dai Cinesi e dagli Indiani, nella quale uno stesso simbolo ha diverso valore se scritto prima di altri, o comunque in una particolare posizione rispetto agli altri.
Si deve poi agli Indiani verso il 7° sec. l’introduzione di un segno per indicare lo zero, necessario tutte le volte che nel numero da rappresentare non compaiono unità di un certo ordine. Il passaggio del sistema dagli Indiani agli Arabi (da qui la denominazione di cifre arabiche) daterebbe dal secolo successivo. Ma nell’Europa cristiana, attraverso la Spagna araba, si diffusero e prevalsero nel 13° sec. non le forme originarie arabo-orientali delle cifre (analoghe a quelle arabe moderne: fig. M), bensì quelle occidentali (cosiddette cifre ghubār), di derivazione diretta dalle indiane. L’importanza che ha lo zero nel sistema di n. decimale fece sì che in Europa, a partire dal 15° sec., si cominciasse a estendere il nome arabo dello zero (sifr donde «cifra») anche alle altre nove cifre significative (solo in inglese cipher continua tuttora a significare «zero»). Secondo altri studiosi, invece, tali cifre sarebbero sbocciate presso i neopitagorici e quindi trasportate in India e in Arabia, per tornare poi in Occidente. Quanto al valore di posizione delle cifre, esso si è formato per gradi e veniva già inconsciamente adoperato nei primi strumenti per calcolare, sia nell’abaco dei Romani, sia in strumenti analoghi presso i Mongoli e i Cinesi. L’introduzione, dapprima in Italia e poi in tutta l’Europa, delle cifre arabiche e del sistema posizionale è in gran parte legata alla diffusione del Liber abaci di Leonardo Fibonacci (1202), preceduto da un trattato sul computo di Guido d’Arezzo nel quale si usavano le cosiddette figure d’abaco (fig. L).
L’uso del principio di posizione è generale, ossia non è affatto limitato alla sola n. con base 10. L’idea è di scrivere ciascun numero come somma di potenze della base del sistema di n.; così, per es., nel sistema decimale
536 = 500+30+6 = 5∙102+3∙10+6;
più in generale, scelto un qualunque intero naturale b>1 come base, ogni intero N si può scrivere in uno e in uno solo modo nella forma
[1] N = cnbn+cn–1bn–1+…+c2b2+c1b+c0,
dove c0, c1, c2 …, cn sono numeri positivi o nulli (esclusa quest’ultima eventualità per cn), inferiori a b. La [1] mostra allora che N si può concepire come la somma di c0 unità del primo ordine, di c1 unità del secondo ordine, di c2 unità del terzo ordine e così via, dove b unità di ciascun ordine formano un’unità dell’ordine successivo. Nel sistema decimale b=10, e quindi le unità dei vari ordini sono tali che 10 unità di un ordine qualunque ne formano una dell’ordine successivo e gli ordini si raggruppano poi a tre a tre in classi, in modo da dar luogo allo specchio seguente:
prima classe
unità semplici (unità del primo ordine)
decine (unità del secondo ordine)
centinaia (unità del terzo ordine)
seconda classe
migliaia (unità del quarto ordine)
decine di migliaia (unità del quinto ordine)
centinaia di migliaia (unità del sesto ordine)
terza classe
milioni (unità del settimo ordine)
decine di milioni (unità dell’ottavo ordine)
centinaia di milioni (unità del nono ordine)
quarta classe
miliardi (migliaia di milioni)
………………… (unità del decimo ordine)
Il numero N si potrà dopo ciò pronunciare (n. parlata), assegnando successivamente il numero delle unità dei vari ordini che lo compongono e scrivere (n. scritta), usando soltanto le 10 cifre 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, corrispondenti ai primi 10 numeri (incluso lo zero).
Sia la n. parlata sia quella scritta procedono da sinistra a destra e iniziano dalle unità di ordine più alto, sicché, per es., il numero formato da 3 migliaia, 2 centinaia, 7 decine e zero unità semplici si scrive 3.270, dove il punto (che spesso in pratica si omette e che talvolta è sostituito da una virgola, per es. nei paesi anglosassoni) indica la separazione tra le unità della prima classe e quelle della seconda classe. Il sistema decimale permette di rappresentare anche i numeri frazionari, con l’introduzione delle unità frazionarie decimali: un decimo, un centesimo, un millesimo… o unità decimali del primo, secondo, terzo… ordine: d1, d2, d3, … ognuna delle quali è tale che 10 di esse rappresentano un’unità dell’ordine precedente. Il numero
formula [2]
si rappresenta allora nella forma
cn cn–1 … c2 c1 c0, d1 d2 … ds
dove la virgola decimale indica la separazione tra la parte intera e la parte decimale (nell’uso anglosassone essa è sostituita da un punto e la parte intera nulla è soppressa: 1.5 = 1,5 e .7 = 0,7). Così, per es., il numero
si può scrivere sotto forma di numero decimale: 35,379. Se però una frazione non può ridursi ad avere come denominatore una potenza di 10, essa può sempre rappresentarsi con un numero decimale periodico, ossia mediante un allineamento decimale infinito, nel quale un gruppo di cifre decimali (eventualmente a partire non immediatamente dopo la virgola) si ripete indefinitamente. Un numero decimale periodico si indica con una scrittura del tipo
cn cn–1 ... c2 c1 c0 , d1 ... ds p1 ... pr ...
essendo cn … c0 la parte intera, d1 … ds l’antiperiodo, p1 … pr il periodo che si ripete indefinitamente, e con l’avvertenza che la parte intera o l’antiperiodo o l’uno e l’altro possono mancare. Per le regole che permettono di risalire da un numero periodico alla sua frazione generatrice e viceversa ➔ periodico. Infine, i numeri irrazionali si possono rappresentare anch’essi con allineamenti decimali, infiniti, i quali tuttavia non risultano periodici.
Sistemi di numerazione
N. a cifre ideografiche; scrittura cuneiforme
Nella notazione cuneiforme (Assiri, Babilonesi, Persiani ecc.) l’unità è rappresentata da un cuneo verticale con la punta in basso: ; la decina con due cunei uniti per la base e disposti ad angolo: ✂. Un cuneo verticale seguito da un cuneo orizzontale con la punta a destra ➤ rappresenta il numero 100. Ripetendo i cunei verticali si formano le centinaia: ➤=200. Il segno del 10, quando è posto a sinistra di quello del 100, ha funzione di moltiplicatore: ✂➤=10×100=1000, similmente ✂✂➤=10×10×100=10.000.
Sistema di n. egiziano
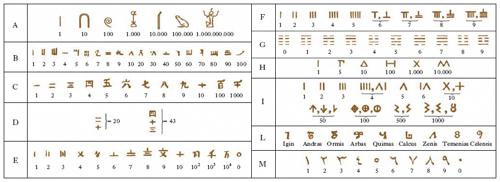
Gli Egiziani nella loro scrittura a caratteri geroglifici, che usavano soprattutto nei monumenti, formavano i numeri con legge additiva dai simboli fondamentali (fig. A). Ogni simbolo è ripetuto tante volte quante è necessario, fino a nove volte, formando eventualmente per ragioni di chiarezza, dei gruppetti di quattro simboli uguali. Nella scrittura ieratica, i numeri si formavano per combinazione additiva dei simboli elencati in fig. B.
Sistema di n. cinese
Presso i Cinesi si hanno tre distinti sistemi di n., tutti a base 10. Quello di uso più frequente è a legge additiva e moltiplicativa e usa i simboli di fig. C. La scrittura procede per colonne verticali che si leggono dall’alto in basso: quando uno dei primi 9 numeri è prima del 10 o di una delle sue potenze, funziona da moltiplicatore; quando è posto dopo, da addendo (fig. D). Si hanno poi altri due sistemi di n. che si leggono orizzontalmente, mettendo a sinistra le unità di ordine più elevato, e sono: la scrittura commerciale e il sistema ad aste (probabilmente di importazione straniera: fig. E e F). Da ricordare infine, i cosiddetti caratteri di Fo-hi (fig. G) che, essendo basati sull’uso di due soli segni (cioè – e -) precorrono, in certo senso, l’attuale sistema binario.
Sistema di n. greco
I Greci usarono per lo più due sistemi di n.: il più antico detto alfabetico o milesio, in uso sin dalla fine dell’8° sec. a.C., si basa sul principio posizionale; esso fa uso di 27 simboli, ossia le 24 lettere dell’alfabeto, e in più, intercalati rispettivamente al 6°, 18° e ultimo posto, tre antichi segni alfabetici caduti poi in disuso: ✂, ✂, ✂ (vau, coppa, sampi). Con queste cifre i Greci potevano esprimere i numeri fino a 999. Per es. σνζ′=257; τπ✂′=386 ecc. Per indicare le migliaia, le decine e le centinaia di migliaia si usavano di nuovo gli stessi 27 simboli nel medesimo ordine, provvisti di un apice (o meglio di uno «iota») a sinistra in basso. Così, per es., π=80.000. In questo modo era possibile rappresentare numeri fino a 999.999.
Un secondo sistema, detto acrofonico, o attico, o erodianeo perché descritto da Erodiano, grammatico del 2° sec. d. C., fu in uso dal 6° sino al 1° sec. a.C. (fig. H) e fu progressivamente sostituito dal precedente.
Sistema di n. etrusco e romano
Gli Etruschi usarono una n. a base decimale, che risentiva di un precedente sistema quinario, fondata sui segni elencati in fig. I, scelti tra i più facili da disegnare e incidere. Questo tipo di n. era usato anche da altri popoli italici, come gli Osci, gli Umbri, i Sanniti ecc.
I Romani usarono gli stessi simboli degli Etruschi, però capovolti e invertiti perché gli Etruschi scrivevano da destra verso sinistra. Tali simboli sono: I (1), II (2), III (3), IV (4), V (5), X (10), L (50), C (100), ∣⊃ (500), ⊂∣⊃ (1000). Il segno ∣⊃ del 500 non è che la metà del segno ⊂∣⊃ del 1000 e finì con il modificarsi in una D, come il secondo in una M. In base alla tabella si ha, per es., MMMCCVII = 1000 + 1000 + 1000 + 100+100+5+1+1=3207. La n. romana è perciò un esempio di sistema di n. a legge additiva. In certi casi, però, la n. romana usa anche la notazione per differenza o sottrattiva, quando, per es., denota il 4 con IV ossia con 5−1. Similmente, XL=50−10=40. In generale si può dire che nella n. romana una cifra che stia immediatamente a sinistra di un’altra che indica un numero maggiore va intesa in senso sottrattivo. Infine, per indicare i numeri superiori a 1000 si usava circoscrivere una coppia di semicircoli al simbolo ϕ; così ⊂ϕ⊃=10.000, ⊂⊂ϕ⊃⊃=100.000 ecc. Più spesso, però, si ricorreva alla semplice sovrapposizione di una lineetta: L̅=50.000, C̅=100.000.
Sistemi di n. posizionale
Generalità
Con una tecnica analoga a quella usata per scrivere i numeri nel sistema decimale si può scrivere qualsiasi numero (naturale, frazionario, irrazionale) in un sistema a base b qualunque, usando soltanto b segni (cifre), rappresentanti i b numeri da zero a b−1.
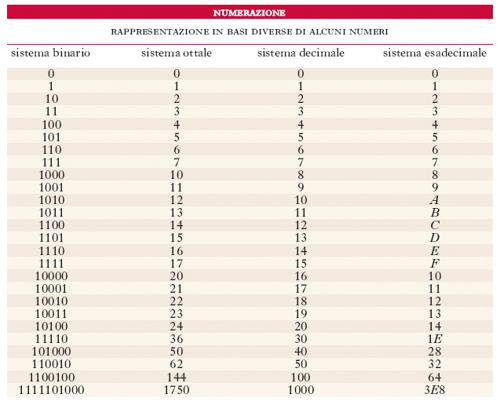
Il numero cnbn+…+c1b+ c0 si indica di solito con il simbolo (cn … c1c0)b, mentre l’indicazione della base e le parentesi si omettono se b = 10, cioè nella scrittura decimale. Così la scrittura (273)8 (che si legge: base 8, 2, 7, 3) indica il numero che, in base 10, si scrive 2∙82+7∙8+3 = 187. Se la base b supera 10 non bastano più le cifre da 0 a 9 e si ricorre di solito alle lettere. In tab. sono scritti i numeri fino a 20 e alcuni multipli di 10 nelle basi 2 (sistema binario), 8 (ottale), 10 (decimale), 16 (esadecimale). Dalla tabella si rileva anzitutto che piccoli valori della base hanno il vantaggio di richiedere pochi simboli ma lo svantaggio che la scrittura dei numeri riesce di un’eccessiva lunghezza.
Anche un qualsiasi numero decimale (con un numero finito o infinito di cifre decimali, periodico o non periodico) può scriversi, come si è già osservato, in una prefissata base b. Così, (73,462)8 = 7∙8+3+4∙8–1+6∙8–2+2∙8–3; (11,0010010000111111…)2 = 1∙2+1+2–3 +2–6+2–11+2–12+2–13+2–14+2–15+2–16+… = π (G. Peano, 1901). Può però accadere che un numero il quale in una base di n. appaia come periodico, in una nuova base sia invece espresso da un numero finito di cifre decimali: per es., (0, 2−)10=(0,2)9. Al contrario, un numero decimale illimitato e non periodico rispetto a una base resta tale in qualsiasi altra base. Si può, dunque, affermare che la sola distinzione tra numeri razionali e irrazionali risulta indipendente dalla base del sistema di numerazione.
Sistema binario
È usato soprattutto negli elaboratori elettronici per la sua estrema semplicità di scrittura, dovuta all’uso di due soli simboli: 0 e 1. I calcoli aritmetici nel sistema binario si eseguono basandosi sulla tabella additiva e sulla tabella moltiplicativa seguenti (la seconda è l’analogo della tavola pitagorica dell’ordinario sistema decimale): +01x010010001110101
In un esempio di moltiplicazione nel sistema binario, se i fattori sono i numeri (11001)2 = 25 e (111)2 = 7; l’operazione si svolge utilizzando le tabelle sopra riportate e seguendo lo stesso schema dell’ordinaria aritmetica decimale:
11001 ×
111 =
11001
11001
1100100
(111)
10101111.
I numeri tra parentesi sono i riporti e il risultato, tradotto in base 10, è 175.
Sistema ottale e sistema esadecimale
Nei calcolatori, che usano internamente la n. binaria, si preferisce spesso impiegare per la presentazione esterna delle stringhe binarie sistemi di n. che abbiano per base una potenza di due: le n. più usate sono la n. ottale (base 8), che usa come simboli i numeri arabi da 0 a 7 e la n. esadecimale (base 16), che usa come simboli base i numeri arabi da 0 a 9 e sei caratteri latini, generalmente da A a F.
Passaggio da un sistema di n. a un altro
Distinguiamo tre casi: il primo riguarda il passaggio dal sistema decimale ad altro sistema: si desideri scrivere 71.519 in base 2; i calcoli necessari sono i seguenti:
71.519 = 2 ∙ 35.579 + 1
35.579 = 2 ∙ 17.879 + 1
17.879 = 2 ∙ 8939 + 1
8939 = 2 ∙ 4469 + 1
4469 = 2 ∙ 2234 + 1
2234 = 2 ∙ 1117 + 0
1117 = 2 ∙ 558 + 1
558 = 2 ∙ 279 + 1
279 = 2 ∙ 139 + 1
139 = 2 ∙ 69 + 1
69 = 2 ∙ 34 + 1
34 = 2 ∙ 17 + 0
17 = 2 ∙ 8 + 1
8 = 2 ∙ 4 + 0
4 = 2 ∙ 2 + 0
2 = 2 ∙ 1 + 0
1 = 2 ∙ 0 + 1.
I resti delle successive divisioni, scritti in ordine inverso, danno la rappresentazione richiesta, che è perciò (10001011111011111)2. Il secondo caso riguarda il passaggio da un sistema in base diversa da 10 al decimale: si desideri scrivere (2307)8 nella base 10; non è consigliabile seguire un procedimento analogo a quello del caso precedente perché le successive divisioni andrebbero eseguite nel sistema ottale; è invece preferibile scrivere (2307)8 = 2∙83+3∙82+0∙8+7 = 1223. Il terzo caso concerne il passaggio da un sistema non decimale ad altro non decimale. Il metodo più consigliabile è di passare dalla base assegnata alla base 10 (caso 2) e poi da questa alla base richiesta (caso 1).
Telecomunicazioni
Negli impianti telefonici a ogni utente viene assegnato un numero che serve a individuarlo; il numero delle cifre costituenti il numero telefonico è in relazione al numero degli utenti della rete. Con due sole cifre si può arrivare al massimo a 100 numeri diversi e quindi a 100 utenti, con 3 cifre a 1000, con 6 a un milione ecc.; in una rete telefonica si ha n. univoca degli utenti quando a ciascun utente corrisponde un numero diverso. La possibilità teorica di adottare una n. univoca estesa a tutti gli utenti di una regione o di una nazione viene limitata dall’opportunità pratica di contenere al minimo il numero delle cifre costituenti il numero telefonico sia per ragioni mnemoniche, sia per ragioni di semplicità di impianti. Così, nei piccoli impianti privati si usa spesso la n. a 2 o a 3 cifre; ma naturalmente tale n. è valida solo nell’ambito dell’impianto stesso. Nelle reti telefoniche a servizio pubblico si sono adottati numeri a 4, 5, 6 e poi 7 o 8 cifre, ma non si è esteso in genere a tutto il territorio di una nazione il criterio di dare un numero diverso a ogni utente; si è invece diviso il territorio nazionale in tante aree con n. univoca, dette distretti telefonici (in Italia 232), e in conseguenza si hanno, in distretti diversi, abbonati contraddistinti con lo stesso numero. L’utente può essere quindi completamente e univocamente individuato solo se il suo numero è accompagnato da quello dell’area di n. (indicativo interurbano) e, nel caso di comunicazioni tra nazioni diverse, anche dal numero della nazione alla quale egli appartiene (indicativo di nazione).