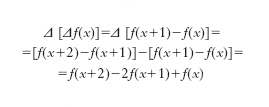differenza
In matematica, il risultato dell’operazione di sottrazione.
Si chiama d. finita prima o brevemente d. prima di una funzione f(x), e si indica con il simbolo Δf(x), l’incremento da essa subito quando alla variabile indipendente x si dà l’incremento 1. In simboli: Δf(x) = f(x+1)−f(x). La d. seconda di f(x) sarà allora la d. della d. prima.
La d. seconda della funzione f(x) si indica con il simbolo Δ2f(x) e così, in generale, la d. n-esima, definita come la d. della d. (n−1)-ma, si indica con Δnf(x). La teoria delle d. finite consente, sotto opportune condizioni, di trovare la soluzione approssimata di equazioni differenziali, anche alle derivate parziali (➔ numerico, calcolo). In particolare, questo metodo permette di calcolare le tavole dei valori di funzioni definite tramite equazioni differenziali. Nel 1812 C. Babbage realizzò la prima macchina (difference engine) che permetteva di effettuare automaticamente tali calcoli.
In statistica, d. media è un indice di variabilità, introdotto da C. Gini, che si ottiene calcolando tutte le d. che si possono eseguire fra i vari termini di una serie e facendo la media delle d. stesse. Essa si dice semplice, quando le d. sono calcolate tra ciascun termine e tutti gli altri; con ripetizione, quando nella media delle d. si tiene conto anche delle d. nulle tra ciascun termine e sé stesso.