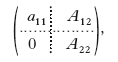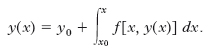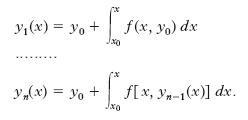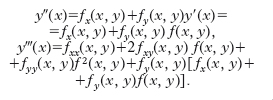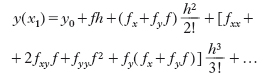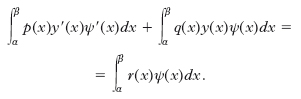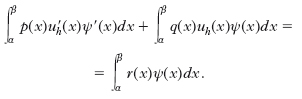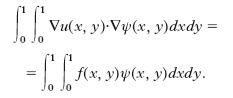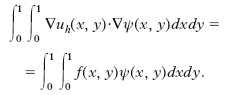numerico, calcolo

Parte dell’analisi matematica che si occupa della ricerca di algoritmi per la risoluzione numerica di problemi quali l’approssimazione di funzioni e l’integrazione di equazioni differenziali ordinarie o alle derivate parziali, quando questi problemi non siano risolubili per via analitica.

Generalità

Il calcolo n. ha ricevuto un grande impulso grazie all’introduzione dei calcolatori, per cui uno dei suoi obiettivi è divenuto la ricerca di algoritmi (procedure deterministiche per risolvere date classi di problemi) per ottenere, mediante un calcolatore, approssimazioni accurate nel minor tempo possibile. I metodi grafici del calcolo n. costituiscono il calcolo grafico (➔ grafico). Storicamente la maggior parte dei metodi n. concerneva l’interpolazione, la risoluzione di equazioni algebriche e trascendenti, il calcolo di integrali definiti e la risoluzione di equazioni differenziali ordinarie con l’uso delle semplici tecniche delle differenze finite. Nelle applicazioni moderne predominano la risoluzione di grossi sistemi di equazioni lineari (e, entro certi limiti, non lineari), l’approssimazione tramite famiglie ortogonali di funzioni e mediante spline, problemi agli autovalori, problemi di ottimizzazione, equazioni differenziali ordinarie e alle derivate parziali.

I metodi n. giocano un ruolo importante anche nella scienza dei calcolatori per i problemi concernenti basi di dati, grafi, metodi di ricerca e ordinamento, decisioni logiche ecc.

Calcoli n. relativi a equazioni

Calcolo delle radici reali di un’equazione algebrica. Sia data l’equazione algebrica (con a₀≠0):

formula [1].

Se i coefficienti sono razionali, essa si può ricondurre a un’equazione algebrica a coefficienti interi per la quale si dimostra che le eventuali radici razionali sono da ricercarsi tra le frazioni che hanno per numeratore un divisore di a_n e per denominatore un divisore di a₀. Se, più in generale, i coefficienti sono reali e l’equazione è di grado ≤4, le sue radici possono determinarsi con operazioni razionali ed estrazioni di radici mediante formule note (➔ equazione), che sono teoricamente ineccepibili, ma che non sempre sono adatte alla valutazione pratica, sia pure approssimata, dei valori n. delle radici. Se n>4, è, in generale, impossibile risolvere per mezzo di radicali l’equazione p(x)=0 (teorema di Ruffini-Abel). In ogni caso si possono indicare procedimenti universalmente applicabili per calcolare con un’approssimazione prefissata (comunque grande) il valore delle radici reali della p(x)=0. A tale scopo conviene procedere prima alla limitazione delle radici reali, poi al calcolo del numero di esse, poi alla loro separazione, e infine al calcolo approssimato di ciascuna radice.

Limitazione delle radici reali. Limitare le radici reali di un’equazione significa determinare un intervallo (l, L) nel quale cadano tutte le sue radici reali. Per determinare un limite superiore L, può servire il teorema di Maclaurin: nessuna radice positiva della [1] può superare

1+ K−−−a₀, dove K è il massimo valore assoluto dei coefficienti negativi che figurano a primo membro dell’equazione.

Un altro metodo, il metodo di Laguerre, si fonda sul fatto che se si divide p(x) per x−α e se i coefficienti del polinomio quoziente e il resto di tale divisione sono numeri tutti non negativi, allora la [1] non ha radici reali maggiori di α. Pertanto, sarà sufficiente attribuire ad α valori crescenti, per es. i valori 1, 2, 3, …, determinando in ciascun caso, con la regola di Ruffini, i coefficienti del quoziente e il resto della divisione, arrestandosi quando tutti questi numeri sono non negativi. Per determinare un limite inferiore l della [1], si possono applicare gli stessi metodi alla trasformata a radici opposte (➔ trasformazione) della [1].

Calcolo del numero delle radici reali. Nell’ipotesi (sostanzialmente non restrittiva) che l’equazione [1] sia priva di radici multiple, il calcolo del numero delle sue radici reali può effettuarsi con l’aiuto del teorema di Sturm. Si determini, col metodo delle divisioni successive, il MCD tra p(x) e p′(x). Posto, per uniformità p₀(x) = p(x) e p₁(x) = p′(x), si ottiene una successione di polinomi di grado decrescente: p₀(x), p₁(x), …, p_k(x) detta catena (o successione) di Sturm relativa all’equazione [1] dove p₂(x), p₃(x), …, p_k(x) sono i resti col segno cambiato delle successive divisioni. Ciò premesso possiamo enunciare il teorema di Sturm: scelti a piacere due numeri a e b (con a<b) per i quali non si annulli p(x), il numero degli zeri di tale polinomio appartenenti all’intervallo (a, b) è dato dalla differenza w(a)−w(b) fra il numero delle variazioni di segno che presenta la catena di Sturm in a e quello che essa presenta in b. Per il calcolo del numero di tutte le radici reali della [1] basterà quindi prendere a e b uguali rispettivamente al limite inferiore l e a quello superiore L della [1].

Separazione delle radici reali. Separare (o isolare) le radici della [1] significa individuare per ciascuna radice reale a dell’equazione due numeri che comprendano fra loro a senza comprendere nessuna altra radice. Il teorema di Sturm consente, oltre alla determinazione del numero delle radici reali, anche la loro separazione. Basterà scegliere, se è necessario con successivi tentativi, opportuni valori appartenenti all’intervallo (l, L) e calcolare per ciascuno di essi il numero delle variazioni presentate dalla catena di Sturm in modo da isolare ciascuna radice.

Estensione dei procedimenti alle equazioni trascendenti. In generale, data un’equazione algebrica o trascendente

[2] f(x) = 0,

determinare le sue radici reali equivale a individuare i punti in cui il grafico della y = f(x) taglia l’asse delle ascisse. Studiandone il grafico, per es. su carta millimetrata, si possono ottenere i valori delle eventuali radici reali sufficientemente approssimati. A volte conviene trasformare la [2] nella forma g(x)−h(x) = 0 e poi considerare le due curve y = g(x) e y = h(x). Le ascisse dei punti d’intersezione di tali curve sono le radici reali della [2]. Con metodi grafici, si potrà in pratica quasi sempre almeno separare le radici reali della [2], cioè costruire intervalli dell’asse reale a due a due privi di punti comuni, contenenti esattamente una radice reale della [2].

fig. 1

fig. 2

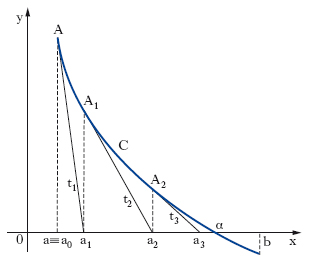
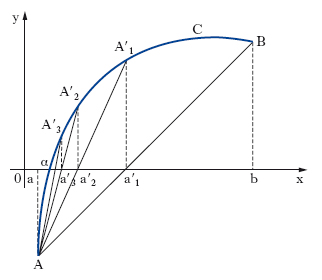
Calcolo delle radici reali di un’equazione. Si consideri un intervallo (a, b) che separa la radice reale α della [2]. Si voglia calcolare un valore approssimato di essa nelle ipotesi che in (a, b): f(x) sia derivabile, f′(x) continua, f″(x) di segno costante, f(a) e f(b) abbiano segni opposti. Tale calcolo si può effettuare in vari modi: per es., con il metodo delle tangenti, o con quello delle secanti: a) metodo delle tangenti o di Newton-Fourier: con le ipotesi poste, per uno solo dei due valori a, b, accade che f(x) e f″(x) hanno il medesimo segno (estremo di Fourier dell’intervallo a, b); sia a₀ tale valore e sia A il punto avente per coordinate, nel piano xy, [a₀, f(a₀)]; A rappresenta quindi (fig. 1) uno dei due estremi dell’arco C che costituisce il grafico della funzione y = f(x) nell’intervallo (a, b), ove si è supposto che l’estremo di Fourier sia a. Si conduca in A la tangente t₁ all’arco C, fino a incontrare l’asse x in un punto di ascissa a₁; questo valore è necessariamente compreso tra l’estremo di Fourier e la radice cercata. Si consideri ora il punto A₁ di C, avente coordinate [a₁, f(a₁)], si costruisca in esso la tangente t₂ a C, sino a incontrare l’asse x in un punto di ascissa a₂, e si ripeta la costruzione quante volte si vuole; si ottiene così una successione di valori a, a₁, a₂, … dalla formula ricorrente: a_k+1 = a_k−f(a_k)/ f′(a_k), per k = 0, 1, 2, … la quale è monotona e tende al valore a cercato; b) metodo delle corde o delle secanti: la retta secante la curva C (fig. 2) nei punti A[a, f(a)] e B[b, f(b)] ha l’equazione [y−f(a)]/[f(b)−f(a)] = (x−a)/(b−a). Tale retta incontra l’asse x nel punto di ascissa a′₁ = [af(b)−bf(a)]/[f(b)−f(a)], e risulta a<α<a′₁. Si può quindi iterare il procedimento ottenendo l’uno dopo l’altro gli elementi di una successione decrescente b, a′₁, a′₂ …, a′_n, … dalla formula ricorsiva (per n≥2):

a′_n = [a′_n–1 f(a)−af(a′_n–1)]/[f(a)−f(a′_n–1)],

che tende al numero α. Si può quindi ottenere un valore approssimato di α (per eccesso nelle nostre ipotesi) con errore piccolo a piacere se n è abbastanza grande.

Calcoli n. relativi a sistemi di equazioni

Sistemi di equazioni lineari. Un sistema di m equazioni lineari algebriche in n incognite si può scrivere nella forma

ovvero AX = B, se con A si indica la matrice m×n dei coefficienti, con X il vettore (colonna a n componenti) delle incognite e con B il vettore (colonna a m componenti) dei termini noti. Poiché la risoluzione di un sistema compatibile a matrice rettangolare può sempre essere ricondotta a quella di un sistema a matrice quadrata il cui determinante è diverso da zero, possiamo limitarci al caso m=n. La soluzione di un tale sistema può determinarsi per mezzo delle formule di Cramer, cioè calcolando opportuni determinanti, ma, per n grande, si preferisce in pratica il metodo di eliminazione o di Gauss. Senza venir meno alla generalità, si può supporre a₁₁≠0. Sottraendo dalla h-ma equazione la prima moltiplicata per a_h1/a₁₁ (h = 2, 3, …, n), si ottiene un sistema equivalente al dato (avente cioè la stessa soluzione) la cui matrice dei coefficienti ha la forma

in cui A₂₂ è una matrice (n−1)×(n−1), 0 indica il vettore colonna composto da n−1 zeri, A₁₂ il vettore riga costituito dagli n−1 coefficienti a₁₂, a₁₃, …, a_1n. Indicati con b′₁, b′₂, …, b″_n i nuovi termini noti, si operi nello stesso modo sul sistema A₂₂X⁽¹⁾ = B⁽¹⁾, dove X⁽¹⁾ indica il vettore colonna di n−1 componenti x₂, x₃, …, x_n e B⁽¹⁾ quello di n−1 componenti b′₂, b′₃, …, b′_n. Ripetendo n−1 volte tale procedimento si perviene a un sistema formato da una sola equazione in un’incognita, da cui si ricava il valore di quest’ultima. Tale valore si sostituisce in una delle due equazioni del sistema immediatamente precedente, e così via.

Questo metodo, quando viene applicato su un elaboratore, ha due grandi svantaggi: l’enorme numero di operazioni aritmetiche che richiede per arrivare alla soluzione, e l’instabilità che deriva da matrici male condizionate, in cui cioè certe righe sono quasi linearmente dipendenti. Per es., per n = 10.000, si debbono effettuare circa 300 miliardi di operazioni aritmetiche. Sistemi con un numero di equazioni da 10 a 50 volte più grande si ottengono, per es., in meccanica dei fluidi, in meteorologia e in geofisica. Si usano, in questi casi, diversi metodi iterativi per approssimare la soluzione con un numero considerevolmente minore di operazioni. I metodi iterativi sono basati sulla decomposizione della matrice A come A = P−Q, dove la matrice P, ottenuta da A, è scelta non singolare e facilmente invertibile. Ponendo R = P^–1Q = I−P^–1A e b̄ = P^–1b, il metodo iterativo viene basato dalla scelta del punto iniziale x⁽⁰⁾, a partire dal quale si definisce la successione x^(k+1) = Rx^(k)+ b̄, dove R è la matrice di iterazione del metodo. La convergenza del metodo alla soluzione esatta x dipende, ovviamente, dalla scelta di P e di x⁽⁰⁾.

Un metodo iterativo è convergente quando la successione di approssimazioni converge alla soluzione esatta indipendentemente dalla scelta di x⁽⁰⁾. Due dei metodi iterativi più usati sono quello di Jacobi e quello di Gauss-Seidel. Il metodo di Jacobi corrisponde alla scelta P = diag(A), e perciò si avrà:

Infatti, se la matrice A è fortemente diagonale dominante (cioè, Σ_i≠j|a_ij|<|a_jj|, 1≤j≤n), il metodo di Jacobi è convergente. Il metodo di Gauss-Seidel, invece, corrisponde alla scelta P = triang.sup.(A), la parte triangolare superiore di A, da cui segue:

Difatti, se la matrice A è irriducibile e fortemente diagonale dominante, il metodo di Gauss-Seidel converge. Inoltre, se il metodo di Gauss-Seidel converge, anche quello di Jacobi converge, ma più lentamente. Se Jacobi diverge, anche Gauss-Seidel diverge.

Problemi algebrici agli autovalori. Sia A una matrice quadrata n×n. Se esistono un vettore non nullo X e un numero λ tali che sia soddisfatta l’equazione AX=λX, allora si dice che λ è un autovalore e che X è un autovettore. L’equazione si può scrivere

(A−λI)X = 0,

cioè come un sistema omogeneo di equazioni, per il quale la condizione per avere soluzioni non banali è f(λ)=det(A−λI)=0. Dunque λ deve essere uno zero di una equazione di grado n che, perlomeno in linea di principio, può essere scritta esplicitamente. È noto comunque che il calcolo degli autovalori eseguito direttamente a partire dall’equazione caratteristica è in generale un procedimento altamente instabile.

Esistono due grandi famiglie di metodi per calcolare gli autovalori di una matrice: metodi iterativi e metodi di trasformazione. Nei metodi iterativi bisogna supporre che uno degli autovalori sia molto più grande degli altri. I metodi di trasformazione si basano sulla proprietà che gli autovalori (ma non gli autovettori) sono invarianti rispetto alle similarità. Per questo si preferisce ridurre la matrice in forma tridiagonale (a_ik=0, per |i−k|>1) e utilizzare la generalizzazione di un metodo, dovuto a K.G.J. Jacobi, basato su ripetute rotazioni bidimensionali. L’idea è quella di scegliere il più grande elemento a_ik fuori della diagonale e di effettuare una rotazione nel piano (x_i, x_k), con l’effetto di rendere uguale a zero il coefficiente trasformato a′_ik. Dopo un numero sufficiente di rotazioni si ottengono gli autovalori sulla diagonale principale, mentre gli autovettori sono dati dal prodotto di tutte le matrici di trasformazione. Se ci limitiamo a costruire matrici tridiagonali, il calcolo può essere compiuto con successive trasformazioni ortogonali: o rotazioni o riflessioni. Per trovare gli autovalori di una matrice tridiagonale simmetrica, si può applicare un elegante metodo iterativo. Come si dimostra facilmente, il valore del polinomio caratteristico in un dato λ può essere ottenuto con il seguente algoritmo:

f_k(λ) = (λ−a_k)f_k–1(λ) −b²_k–1 f_k–2(λ); f_–1 = 0, f₀ = 1,

dove (a₁, a₂, …, a_n) è la diagonale principale e (b₁, b₂, …, b_n–1) ciascuna delle due diagonali adiacenti. Se la matrice originale non è simmetrica, si può trasformare in una forma opportuna, detta di Hessenberg, e per la quale esiste un’unica fattoriz;zazione A=QR, dove Q è unitaria e R è triangolare superiore. In pratica i calcoli si eseguono costruendo una successione di matrici i cui elementi tendono agli autovalori.

Sono anche molto utili algoritmi che, attraverso l’iterazione dell’applicazione lineare definita da una matrice, individuano l’autovalore più grande della matrice stessa e il suo relativo autovettore. Il principio di questi algoritmi è estremamente semplice. Sia data una matrice A con autovalori reali di cui si voglia calcolare l’autovalore λ di valore assoluto più grande e si supponga qui per semplicità che esso abbia molteplicità geometrica, cioè dimensione del sottospazio generato dagli autovettori a esso associati, uguale a 1 (in certi casi, come per es. nelle matrici stocastiche, queste ipotesi non sono molto restrittive). Definendo l’applicazione iterativa ν′=(Aν)/∥Aν∥, essa converge esponenzialmente all’autovettore normalizzato relativo all’autovalore λ cercato. Quest’idea può essere opportunamente generalizzata ad autovalori λ con molteplicità geometrica più grande di 1 e al caso di autovalori complessi. Gli algoritmi così ottenuti sono molto adatti all’implementazione su elaboratori elettronici e a questo è dovuto il notevole studio che è stato loro dedicato.

Equazioni differenziali

Risoluzione n. del problema di Cauchy. Sia dato in forma normale un sistema di equazioni differenziali ordinarie del primo ordine

y′_i = f_i(x, y₁, y₂, …, y_p) (i = 1, 2, …, p).

Ordinariamente non interessa determinare tutti gli integrali del sistema, ma piuttosto risolvere il cosiddetto problema di Cauchy, determinare cioè un integrale y₁(x), y₂(x),…, y_p(x) del sistema che verifichi le p condizioni iniziali

y_i(x₀) = ȳ_i (i = 1, 2, …, p),

essendo x₀, ȳ_1, ȳ₂, ..., ȳ_p numeri assegnati, risolubile purché siano verificate determinate ipotesi sulla continuità e derivabilità delle funzioni f_i in un intervallo I.

Metodo di Ch.-E. Picard e L.L. Lindelöf per l’integrazione numerica delle equazioni differenziali. - Un importante metodo d’integrazione numerica è fondato sulla trasformazione dell’equazione differenziale in un’equazione integrale. Immaginando di sostituire in f(x,y) la funzione incognita y con la sua espressione y(x) supposta conosciuta, si possono integrare ambo i membri dell’equazione differenziale y′= f[x, y(x)], ottenendo l’equazione integrale:

Si consideri ora la successione di funzioni {y_n(x)} così definita ricorsivamente:

Si dimostra che questa successione converge rapidamente in I verso la funzione richiesta y(x). Essendo la successione effettivamente costruibile, un termine dopo l’altro, si può, calcolando un opportuno numero di termini di essa, ottenere con buona approssimazione l’integrale particolare dell’equazione differenziale che verifica la condizione iniziale data. Questo metodo si può estendere a un sistema di equazioni differenziali.

Metodi a passo singolo (one-step). - Molti altri metodi si fondano sulle seguenti considerazioni. Per il calcolo approssimato di y(x) nel punto x ∈ I, supposto, per fissare le idee, x>x₀, si suddivida innanzitutto l’intervallo (x₀, x) in n intervalli parziali, tutti uguali per semplicità, mediante i punti x₀, x₁, …, x_n=x. Indichiamo con h la lunghezza (x−x₀)/n di ciascun intervallo parziale. Partendo dal valore iniziale y₀=y(x₀) è possibile costruire successivamente una tabella di valori y₁, y₂, …, y_n ordinatamente approssimati a y(x₁), y(x₂), …, y(x) in questo modo. Sviluppiamo in serie di Taylor:

D’altra parte, da y′ (x)=f(x,y) si ha successivamente:

Quindi, indicando semplicemente con f, f_x, … i valori assunti dalla funzione e dalle derivate successive nel punto noto (x₀, y₀), si ha:

Troncando a un certo punto lo sviluppo in serie, si ottiene il numero y₁, valore approssimato di y(x₁). Ripetendo lo stesso procedimento si ottengono successivamente i valori y₁, y₂, …, y_n. In pratica, per semplificare i calcoli, all’ultima formula se ne sostituisce una del tipo

o, in generale, per ottenere y_r+1 da y_r, si pone

dove ϕ(x, y, h) è un’opportuna funzione che

verifica la condizione lim_h→0 ϕ(x, y, h)=f(x, y)

nel campo R. A seconda del modo di esprimere la funzione ϕ(x, y, h) si distinguono vari metodi. Si dice che il metodo è di ordine p se, posto

r(x, h)=y(x+h)−y(x)−hϕ[x, y(x), h],

risulta r(x, h) infinitesimo di ordine superiore ad h^p+1 al tendere di h allo zero. In tab. sono riportati alcuni dei metodi più in uso; per ciascuno di essi è indicato il modo di calcolare la funzione ϕ(x, y, h) a partire dalla funzione nota f(x, y), e l’ordine del metodo.

Metodi a passi multipli (multi-step). Differiscono dai precedenti perché nel calcolo di y_r+1 intervengono anche i k precedenti valori y_r, y_r–1,.., y_r–k+1, con k>1. Si fa uso di una formula del tipo:

yr+1 + a1yr + … + akyr−_k+1 =

= h(b0 fr+1 + b1 fr + … + bk fr−k+1),

dove si è posto f(x_r, y_r) = f_r. Se b₀ = 0 la formula fornisce esplicitamente y_r+1 e si dice di tipo aperto o anche formula di predizione. Se invece b₀≠0 la formula fornisce solo implicitamente y_r+1 e si dice di tipo chiuso o anche formula di correzione. Spesso una formula di tipo aperto è meno accurata di una di tipo chiuso, e pertanto si fa uso della prima per ‘predire’ y_r+1 e calcolare f_r+1, e della seconda per ‘correggere’ y_r+1 sostituendovi a secondo membro il valore f_r+1 precedentemente trovato. Nel metodo di Milne, per es., si hanno le seguenti formule:

Risoluzione n. di problemi con condizioni al contorno. - La situazione è diversa se si vuole risolvere un problema di valori al contorno. L’equazione del secondo ordine −(p(x)y′)′+q(x)y = r(x) con coefficienti p, q, r continui, dove p ha derivata continua e p(x)≥c₀>0, ∀x∈ (α, β), ha sempre un’unica soluzione sia con le condizioni iniziali y(x₀)=y₀, y′(x₀)=y′₀, sia con le condizioni sul contorno y(α)=A, y(β)=B. Quando non si conosce la soluzione del problema ai valori al contorno in modo esplicito, si vogliono trovare delle approssimazioni u_j di y(x_j), 1≤j≤n−1, avendo posto x₀=α, x_n=β. A tale scopo esistono vari metodi basati sia sulla risoluzione di problemi ai valori iniziali associati, sia direttamente sui valori al bordo. Fra i primi, il metodo dei tiri successivi (shooting) consiste nel trovare le soluzioni v, w dei problemi ai valori iniziali −[p(x)v′]′+q(x)v = r(x)/A, v(α)=1, v′(α)=0, e −[p(x)w]′+q(x)w=0, w(α)=0, w′ (α)=1, e quindi nel prendere u=Av+sw, dove s=[B−Av(β)]/w(β) è definito in modo unico quando w(β)≠0. Se w(β)=0 e B=Av(β), s può essere scelto in modo arbitrario. Infine, per w(β)=0 e B≠Av(β), il metodo non genera mai una funzione con valore B sul punto β e dunque non può essere usato.

Tra i metodi diretti più usati si trovano quello alle differenze finite, quello agli elementi finiti e quelli spettrali. Il metodo alle differenze finite è basato sulla discretizzazione delle derivate tramite quoziente di differenze. Per il problema preso in considerazione, scegliendo un reticolo uniforme, il metodo consiste nel trovare delle approssimazioni U_j di u(x_j) come soluzioni del sistema algebrico lineare

con 1≤j<n, completato dalle ovvie relazioni U₀=A, U_n=B, dove abbiamo posto:

Si può verificare che la matrice di questo sistema è fortemente diagonale dominante e quindi non singolare, e pertanto il sistema ha sempre una e una sola soluzione. Il metodo agli elementi finiti è basato su formulazioni deboli del problema ottenute tramite integrazione per parti. Supponiamo A=B=0. Sia ψ una funzione con derivata continua nell’intervallo (α, β) tale che ψ(α)=ψ(β)=0. Integrando per parti si ottiene la formulazione debole:

Viceversa, se y è una funzione con derivata continua che soddisfa la relazione precedente per ogni funzione y che si annulla sul contorno, allora y è anche una soluzione del problema ai valori al contorno (omogeneo) in considerazione. Si può dimostrare che la formulazione debole vale anche con condizioni meno restrittive. Uno spazio di elementi finiti molto usato è quello dei polinomi definiti a tratti lineari, globalmente continui, che si annullano sui punti del contorno:

Questo è un sottospazio vettoriale di V di dimensione n−1. Una base molto utile per tale spazio è data dalle funzioni ‘cappello’ ψ_j(x_j)=1, ψ_j(x_j−1)=ψ_j(x_j+1)=0, 1≤j≤n−1.

Il metodo di Galerkin consiste nel trovare u_h è V_h tale che, per ogni ψ ∈ V_h, valga la relazione:

Usando la base di V_h sopra specificata, le relazioni precedenti generano un sistema algebrico lineare tridiagonale nelle componenti di u_h, con matrice fortemente diagonale dominante; di conseguenza, il sistema ammette sempre un’unica soluzione, che si deriva molto velocemente grazie alla struttura della matrice. Infine, i metodi spettrali sono basati su sviluppi delle funzioni in serie di polinomi ortogonali (per es., di Legendre o di Čebyšev).

Risoluzione n. di equazioni differenziali alle derivate parziali. I metodi qui discussi sono per due dimensioni spaziali ma esistono dei metodi analoghi per il caso tridimensionale. Le equazioni alle derivate parziali vengono raggruppate in ellittiche, paraboliche e iperboliche. Fondamentale è l’equazione di Poisson (detta anche equazione dei potenziali)

dove ∇² è l’operatore laplaciano e Ω è un dominio aperto semplicemente connesso in R². Per l’equazione di Poisson presenteremo un metodo alle differenze finite e uno agli elementi finiti. Supponiamo, per semplicità Ω=(0, 1)×(0, 1) sul quale definiamo un reticolo uniforme come segue. Fissato un numero naturale n, scegliamo i nodi (x_i, y_j), 0≤i, j≤n, dove x_i=i/n, y_j=j/n. Il metodo alle differenze finite definisce una funzione di reticolo U_i,j, 0≤i, j≤n, approssimante i valori di u(x_i, y_j) come soluzione di un sistema di equazioni algebriche lineari. Per avere una soluzione unica dell’equazione differenziale si deve conoscere una condizione sul contorno, che, per semplicità, supporremo del tipo Dirichlet, cioè supporremo che valga la condizione u(x, y) = g(x, y), dove g(x, y) è una funzione assegnata sulle (x, y) ∈ Γ = ∂Ω. Ponendo h=1/n, si definisce U_0,j=g(0, y_j), U_n,j=g(1, y_j), U_i,0 = g(x_i, 0), U_i,n = g(x_i, 1), 0 ≤ i, j ≤ n, su Γ, e (1/h²) (U_i+1,j–2U_i,j+U_i–1,j)+(1/h²) (U_i,j+1–2U_i,j+U_i,j–1)=f(x_i, y_j), 1≤i, j≤n−1 all’interno di Ω. Si può dimostrare che questo sistema ammette un’unica soluzione, convergente a quella esatta con un errore di ordine h². Leggermente più complicato è il trattamento di altri insiemi Ω e di condizioni al contorno di tipo Neumann (condizioni sulla derivata normale della soluzione sul contorno) o miste. Il metodo agli elementi finiti è formalmente identico a quello presentato per le equazioni ordinarie. Poniamo

,

spazio delle funzioni bilineari a tratti, globalmente continue, che si annullano sul contorno. Una sua base molto utile è data dalle funzioni ‘cappello’ ψ_ij(x_i, y_j)=1, ψ_ij(x_i–1, y_j)=ψ_ij(x_i+1, y_j)=ψ_ij(x_i, y_j–1)=ψ_ij(x_i, y_j+1)=0, 1≤i, j≤n−1. Per ogni funzione ψ ∈ V_h, risulta dalla formula di Green la seguente forma debole del problema di Dirichlet:

Il metodo di Galerkin consiste nel trovare u_h ∈ V_h tale che, per ogni ψ ∈ V_h, sia:

Queste equazioni conducono a un sistema algebrico lineare nelle componenti di u_h, il quale è sempre non singolare e, per un ordinamento giusto delle variabili (da sinistra verso destra, dal basso verso l’alto), ha una matrice simmetrica a bande (tridiagonale più due diagonali minori), per cui risulta essere rapidamente risolubile (per es., con i metodi iterativi di Gauss, Gauss-Seidel o diretti). La matrice ha una struttura analoga nel caso delle differenze finite. Geometricamente il metodo consiste nel costruire una maglia triangolare che sia più fitta nelle zone dove si possono prevedere rapide variazioni delle funzioni. Le parti della maglia, in questo caso triangoli, sono dette elementi. Al di sopra di ciascun nodo poniamo un punto ad altezza 1: in questo modo definiamo una piramide che a sua volta rappresenta una funzione base. Quindi possiamo approssimare la superficie cercata u(x, y) con figure piane, proprio come si può approssimare una linea curva mediante segmenti. Facendo uso di questo metodo n., la regione nella quale si vuole studiare la soluzione dell’equazione differenziale data non viene ridotta a una struttura reticolare, come nel metodo delle differenze finite, ma è suddivisa in elementi all’interno di ciascuno dei quali la funzione incognita è rappresentata da un polinomio nelle variabili spaziali. Il grado di questo polinomio non è arbitrario, ma dipende dal numero di nodi dell’elemento, dal numero di gradi di libertà di ciascun nodo e dalla condizione di continuità fra un elemento e gli elementi adiacenti. Gli elementi usati per lo studio di regioni bidimensionali sono generalmente triangolari, talvolta anche rettangolari del primo ordine, in cui cioè le variazioni della funzione incognita sono lineari nelle variabili spaziali, e di ordine superiore o isoparametrici, che posseggono un numero di nodi maggiore del numero di vertici dell’elemento e consentono una variazione quadratica o cubica della funzione stessa. Nel caso in cui lo studio sia effettuato in regioni tridimensionali si utilizzano generalmente elementi prismatici o tetraedrici a base quadrata e, più raramente, a base triangolare. Almeno a livello applicativo è possibile porre a confronto questo metodo n. con quello alle differenze finite, che insieme al metodo degli elementi finiti è il più usato. Si può dire che i reticoli alle differenze hanno una struttura regolare e quindi facilmente determinabile, mentre quelli agli elementi finiti presentano una struttura con forma e disposizione degli elementi che godono di una maggiore libertà, permettono cioè di discretizzare più facilmente una struttura continua, anche se diviene più laborioso ricavare le matrici dei coefficienti di discretizzazione.

Per l’equazione del calore possono usarsi gli stessi metodi utilizzati per l’equazione di Poisson, discretizzando inoltre la derivata temporale mediante differenze finite. Occorre avere sia condizioni sul contorno, sia condizioni iniziali, quali u(0, x, y)=u₀(x, y), per (x, y) in Ω. Per l’equazione delle onde, invece, questa equazione deve completarsi con i valori al contorno e (essendo del secondo ordine nel tempo) con due condizioni iniziali, u(0, x, y)=u₀(x, y), ∂u/∂t(0, x, y)=v₀(x, y), che supporremo compatibili con i valori al contorno.

Equazioni integrali

La risoluzione n. di equazioni integrali si riconduce generalmente a un sistema di equazioni e a un problema agli autovalori.