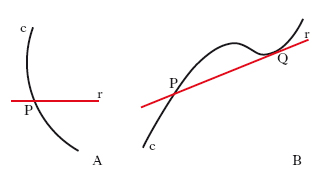
secante
secante In geometria, retta s. (o semplicemente s.) una curva piana c in un punto P è ogni retta r che passi per P e non sia tangente in P a c (fig. A); può però accadere che una retta r s. in P sia tangente alla curva c in un altro punto Q (fig. B); si chiama piano s. il piano che interseca una superficie senza essere tangente; con significato analogo, si dicono s. due curve nel piano, o due superfici nello spazio, che non sono tangenti (cioè ammettono nel punto considerato rette tangenti distinte, o rispettivamente piani tangenti distinti).
In trigonometria, s. di un angolo α (secα, come simbolo), funzione trigonometrica uguale all’inverso del coseno di α; non è definita per gli angoli (come l’angolo retto) in cui il coseno si annulla.
Nel calcolo numerico, metodo delle s., metodo che permette di trovare valori approssimati delle soluzioni di un’equazione e che si applica quando non si è in grado di determinare le soluzioni esatte dell’equazione stessa (➔ numerico, calcolo).