grafico
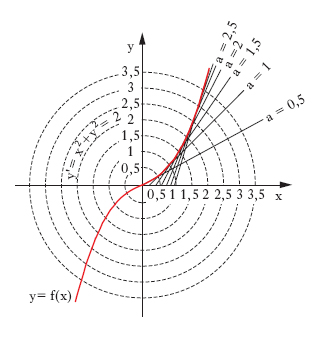
Rappresentazione schematica dell’andamento di un fenomeno o di un’attività (➔ diagramma). Il ricorso a un g. permette sia di rappresentare sia di effettuare direttamente alcune operazioni di matematica: i procedimenti di calcolo grafico abbracciano vasti settori del calcolo matematico e hanno trovato larga applicazione nella statistica, nella tecnica ecc. per la loro rapidità e praticità. Rientrano in questo campo i procedimenti di interpolazione e di estrapolazione grafica, di derivazione e di integrazione grafica, la nomografia, la statica grafica, e in senso lato anche la geometria descrittiva con i suoi metodi grafici per la risoluzione dei problemi geometrici. I procedimenti di calcolo grafico sono stati, però, via via sostituiti da procedimenti di calcolo numerico mediante l’uso dell’elaboratore elettronico. Nella fig. si dà, a titolo di esempio, la determinazione grafica delle soluzioni di un’equazione differenziale ordinaria del 1° ordine; consideriamo l’equazione y′=x2+y2, che non è integrabile elementarmente; si può procedere alla sua integrazione grafica con il cosiddetto metodo delle isocline. Tracciata in un piano cartesiano una famiglia di curve y′=cost, cioè x2+y2=cost, si immagini condotto in ciascun punto di una di esse un elemento di retta avente il coefficiente angolare a pari al corrispondente valore di y′. Una soluzione y=f(x) dell’equazione proposta ha come g. una curva integrale ottenuta ‘raccordando’ con continuità gli elementi di retta nominati, a partire dal punto iniziale. Il procedimento è tanto più preciso quanto più numerose sono le isocline, ed è utilmente applicabile, più in generale, alle equazioni del tipo y′=f(x, y), ogni qual volta sia facile tracciare le curve f(x, y)=cost.