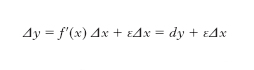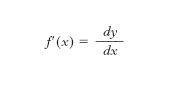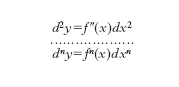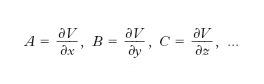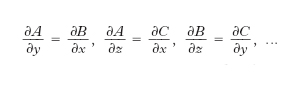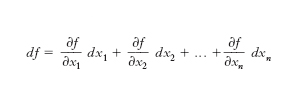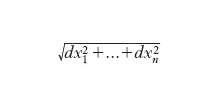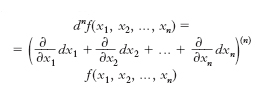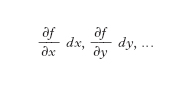differenziale

Economia

Dazio d. Dazio che si applica su merci provenienti da paesi con cui si è in guerra doganale o a essi dirette, e che è perciò superiore a quello imposto sulle stesse merci importate o esportate da o verso gli altri paesi.

Politica commerciale d. Politica che discrimina tra paese e paese, riservando ad alcuni posizioni di privilegio e ad altri d’inferiorità, mediante dazi e diritti vari, divieti, licenze, esclusioni ecc.

Rendita d. (o ricardiana) Rendita di cui gode un proprietario fondiario per il fatto di possedere un terreno più fertile di altri pure messi a coltivazione, o più vicino al mercato di sbocco: è un guadagno extra che deriva da una situazione di mercato (➔ rendita).

Guadagni (o redditi) d. Di natura analoga alla rendita d., sono i redditi percepiti da tutti i proprietari di fattori produttivi durevoli o di beni durevoli di consumo, assolutamente irriproducibili o intrasferibili o che non si possano trasferire entro il periodo necessario per riprodurli (quasi-rendite), qualora la domanda risulti improvvisamente superiore all’offerta.

Tariffa d. Tariffa applicata sui prezzi di trasporto, per es. nelle ferrovie; la sua base o prezzo per unità di traffico (viaggiatore-chilometro, tonnellata-chilometro) non è costante ma varia a seconda della lunghezza del percorso. La tariffa d. a base decrescente può stabilire prezzi unitari diversi applicabili all’intero percorso o a tratti successivi di percorso; in questo secondo caso, tecnicamente più perfetto, si evitano bruschi salti nel passaggio dall’applicazione di una base all’altra. La tariffa d. a base crescente, che si dice anche vicinale, si applica esclusivamente per le brevi distanze (per es. collegamento tra capoluogo di provincia e centri minori) entro le quali conviene allo Stato favorire i viaggi brevissimi per vincere la concorrenza di altri mezzi di locomozione.

Contratti d. I contratti di borsa a termine, perché in genere con essi non s’intende ritirare o consegnare effettivamente i titoli ma solo speculare sulle previste differenze tra le quotazioni alla stipulazione e alla scadenza del contratto.

Fisica

La qualifica di d., che si dà a una grandezza variabile definita come rapporto di altre due, significa generalmente che la grandezza in questione, A, viene definita non come rapporto tra valori finiti delle altre due, A=B/C, ma come rapporto tra variazioni corrispondenti infinitesime, A′=dB/dC. La definizione d. di una grandezza ha ragion d’essere quando si è in presenza di grandezze non proporzionali, poiché in tal caso il rapporto B/C tra due valori finiti di B e di C darebbe soltanto un valore medio di A, generalmente diverso dai suoi vari valori istantanei o locali.

Con diverso significato, viene data a una grandezza la qualifica di d. per indicare la differenza tra i valori di essa in corrispondenza a due situazioni fisiche diverse. Così, per es., in termodinamica, si parla di volume d. per indicare la differenza tra il volume specifico del vapore secco e quello del liquido alla stessa temperatura.

Matematica

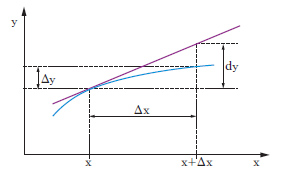
Per una funzione di una variabile, che sia derivabile, ha il nome di d., o d. primo, la parte principale dell’incremento che essa subisce per un incremento della variabile indipendente. Precisamente, data una funzione y=f(x), sia Δy l’incremento che essa subisce in conseguenza di un incremento Δx della variabile indipendente x. Se Δy si può approssimare efficacemente con un’opportuna funzione di primo grado aΔx, nel senso che la differenza Δy−aΔx risulti infinitesima di ordine superiore al primo rispetto all’infinitesimo Δx, allora aΔx si chiama d. della funzione f(x) e si indica con il simbolo dy, o anche con df. Si dimostra che l’esistenza del d. si accompagna sempre a quella della derivata, e che risulta a=f′ (x) (ove f′ è la derivata di f). In formule si ha:

fig. 1

in cui ε è una quantità che tende a zero quando Δx tende a zero. Sostituire all’incremento Δy della funzione il corrispondente d. significa, da un punto di vista geometrico, sostituire (fig. 1) alla curva y=f(x) la tangente a essa nel punto considerato, che ha per coefficiente angolare proprio f′(x). Poiché infine risulta, per la funzione x stessa, dx=Δx, si può scrivere in generale l’espressione: dy=f′(x)dx e quindi anche:

Quest’ultima formula mostra a sua volta che la derivata si può pensare come rapporto di due d., quello della funzione e quello della variabile indipendente, e giustifica pertanto l’antica denominazione di quoziente d. per la derivata. Il d. di una funzione gode di proprietà formali analoghe a quelle della derivata: per es., il d. della somma di due funzioni è uguale alla somma dei d. ecc. Il d. è dunque un esempio importante di funzionale lineare; si tratta, anzi, di un funzionale misto perché dipende sia dalla funzione sia dal valore della variabile indipendente.

Si dice d. secondo di una funzione il d. del d. primo; si indica con d²f; e analogamente il d. n-esimo, o di ordine n, è il d. del d. (n−1)-esimo: dⁿf=d(dⁿ⁻¹f). Convenendo di riguardare il d. dx della variabile come indipendente dalla x (il che è lecito se x è effettivamente una variabile indipendente), risulta:

D. esatto Locuzione con cui si designa una forma d. lineare A(x,y,z,...)dx+ B(x,y,z,...)dy + C(x,y,z,...)dz + ... che sia il d. totale di una certa funzione V(x,y,z,...), detta potenziale, ciò accade se

,

Condizione necessaria e sufficiente perché la forma d. sia un d. esatto è che

,

D. totale (primo) di una data funzione f(x₁, x₂,..., x_n), è l’espressione

essa differisce dal corrispondente incremento della funzione per un infinitesimo di ordine superiore rispetto a formula.

Dal punto di vista geometrico l’esistenza del d. per una funzione di due variabili equivale all’esistenza del piano tangente alla superficie z=f (x, y). D. totale di ordine n è invece l’espressione

ove il simbolo a secondo membro indica la potenza simbolica n-esima del d. totale primo.

D. parziali di una funzione f(x, y,...) rispetto alle variabili x, y, ... sono le espressioni

,

Calcolo d. Quella parte dell’analisi matematica che si occupa di tutte le svariate questioni che più o meno direttamente si collegano ai fondamentali concetti di derivata (ordinaria e parziale) e di d. delle funzioni (➔ derivata e, anche per la parte storica, analisi).

Calcolo d. assoluto Teoria concettuale (e nel tempo stesso tecnica di calcolo) che permette di tradurre le proprietà geometriche e fisiche dello spazio in forma analitica indipendente dalla scelta particolare delle coordinate cui lo spazio s’intende riferito. A fondamento del calcolo d. assoluto è la nozione di tensore, onde esso è detto anche calcolo tensoriale (➔ tensore).

Tecnica

fig. 2

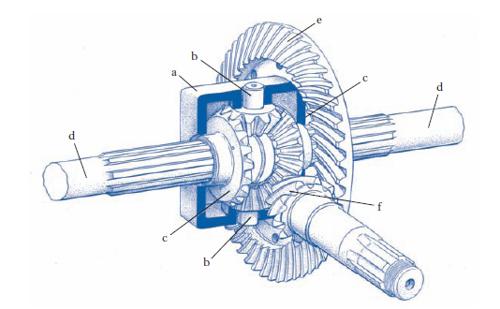
In meccanica, termine usato per indicare un rotismo epicicloidale a ruote coniche nel quale la velocità angolare del membro conduttore è uguale alla media delle velocità delle due ruote condotte. L’applicazione più nota e diffusa è quella alla trasmissione del moto alle ruote motrici degli autoveicoli (fig. 2). Il membro conduttore è costituito da una scatola a, in cui sono inseriti radialmente due o più pignoni conici (satelliti) b, che ingranano con le due ruote coniche planetarie c solidali con i relativi semiassi d delle ruote motrici. Il moto è comunicato alla scatola dei satelliti a da una corona dentata conica e solidale a essa, accoppiata a un pignone conico f solidale con l’asse di trasmissione. Se il veicolo si muove in linea retta le due ruote planetarie mantengono velocità angolari uguali tra loro e uguali a quella dell’asse. Quando invece il veicolo percorre una curva, la ruota che descrive la circonferenza di raggio maggiore accelera e quella che percorre la circonferenza minore rallenta, mentre la velocità della gabbia dei satelliti, e quindi quella della trasmissione e del motore, rimane invariata. D. autobloccante D. utilizzato nei veicoli fuoristrada quando una delle due ruote tende a slittare (➔ autobloccante).

D. centrale D. che, in un’automobile a quattro ruote motrici, trasmette il moto ricevuto dal motore, tramite il cambio, sia all’asse anteriore sia all’asse posteriore, ripartendo in modo opportuno la coppia tra i due assi.

D. controllato (o comandato) Particolare tipo di d. impiegato nei veicoli cingolati, come i carri armati, nei quali funziona da ripartitore del moto e da dispositivo di sterzo.