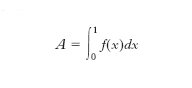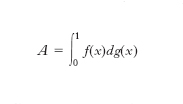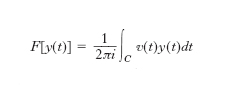funzionale

In matematica, variabile y che dipende non da una o più variabili, ma da una funzione f; in simboli: y=F(f). Un f. non è da confondere con una funzione composta (o funzione di funzione): la y è f. di f(x), se la funzione stessa f(x) è concepita come una variabile, e a ogni scelta della funzione f(x) corrisponde un valore per y. Per es., in un piano, l’area A della superficie limitata dall’asse x, dall’asse y, dalla retta x = 1 e dalla curva di equazione y=f(x) è un f. di f(x), e risulta:

F. lineare è un f. F tale che: F(f₁+f₂)=F(f₁)+F(f₂); il f. dell’esempio è lineare. Un altro esempio importante di f. lineare è dato dall’integrale di Stieltjes

dove f(x) è una funzione continua e g(x) una funzione a variazione limitata: introdotta, nello spazio funzionale C che ha come elementi le funzioni continue, una opportuna topologia, esso risulta un f. continuo; inoltre un teorema di Riesz afferma che ogni f. lineare e continuo si può rappresentare in tale modo, a patto di scegliere opportunamente la funzione g(x).

F. analitici sono quelli caratterizzati dalle proprietà: a) sono definiti in campi di funzioni analitiche; b) applicati a funzioni y(t, a) che siano analitiche sia rispetto alla t sia rispetto a uno o più parametri a, danno luogo (quando nella loro applicazione la y si consideri come funzione della sola t) a funzioni analitiche dei parametri. A base della teoria dei f. è stato posto, da L. Fantappiè, il fatto che qualunque f. analitico lineare F individua una funzione analitica v, chiamata indicatrice di F, e riesce a sua volta completamente caratterizzato da questa funzione nel senso che si può ottenere il valore di F per una qualsiasi funzione y(t) del suo campo di definizione, in base alla formula integrale

dove la curva d’integrazione C è una curva chiusa che contiene nell’interno tutti i punti singolari della funzione y(t) variabile indipendente, ma lascia all’esterno tutti i punti singolari della funzione indicatrice υ(t), caratteristica del funzionale F. Con questo risultato, che collega a ogni f. analitico lineare F una funzione analitica υ(t) (la sua indicatrice), e viceversa, tutte le proprietà del f. lineare si vengono a riflettere in proprietà della funzione indicatrice, e inversamente; cosicché la determinazione e lo studio di tutti i f. lineari si riduce allo studio delle varie funzioni analitiche, già ampiamente sviluppato, per classi di funzioni importanti, nell’analisi ordinaria.

L’ analisi funzionale è il capitolo della matematica che tratta dei funzionali. È merito di V. Volterra (1887) e di J. Hadamard (1910) l’aver introdotto i concetti di funzione di linea e di funzione di una funzione o f., estendendo a questi le nozioni fondamentali dell’analisi ordinaria. Successivamente M. Fréchet e H. Moore hanno sviluppato su questa base la cosiddetta analisi generale, nella quale le variabili possono essere di natura qualunque (numeri, funzioni, enti geometrici ecc.) e sono possibili opportune estensioni delle nozioni fondamentali dell’analisi ordinaria, come quella di limite e di differenziale. L’analisi funzionale ha importanti applicazioni nella teoria delle equazioni differenziali, delle equazioni integrali, nel calcolo delle variazioni, nella fisica matematica, giovandosi, soprattutto nello studio di problemi non lineari, di importanti strumenti matematici come il teorema di punto fisso (di Brouwer), la teoria di Morse, delle biforcazioni ecc.

Integrale funzionale Tipo di integrale (detto anche, specialmente in fisica teorica, integrale sui cammini) in cui la variabile di integrazione è essa stessa una funzione (➔ cammino).