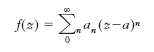analitico

Filosofia

Nella logica kantiana, giudizio a. è quello nel quale il concetto del predicato è implicitamente contenuto nel concetto del soggetto, e in cui quindi basta analizzare il soggetto per ricavarne il predicato (per es. i corpi sono estesi). Il giudizio a., fondato sul principio d’identità e di non contraddizione, è a priori, cioè vero necessariamente e universalmente, ma è infruttuoso, perché non estende la conoscenza, ma la chiarisce soltanto. linguistica Si dicono a. le lingue che per esprimere rapporti sintattici ricorrono di preferenza a preposizioni, posposizioni, verbi ausiliari ecc., mentre le lingue sintetiche usano esprimere tali rapporti per mezzo di desinenze e variazioni tematiche.

Matematica

Una funzione della variabile reale x, f (x), si dice funzione a. reale nell’intervallo (a−d, a+d) se in esso è sviluppabile in serie di Taylor:

Le trascendenti elementari (e^x, log x, sen x ecc.) sono funzioni analitiche. Una funzione complessa

della variabile complessa z=x+i y si dice a. (o monogena o olomorfa) in un certo dominio A del piano complesso, se è derivabile in ogni punto di A, cioè se il quoziente

tende a un ben determinato limite f′ (z₀), quale che sia il modo in cui Δz tende allo zero, quando z₀ è interno ad A. Tale limite esiste se e soltanto se le funzioni u e v soddisfano alle condizioni di Cauchy-Riemann, o condizioni di monogeneità o di olomorfia:

Da ciò segue che la parte reale, u, e il coefficiente dell’immaginario, v, di una funzione a. sono funzioni armoniche. Se ora a è un punto di A, si indichi con R il raggio del massimo cerchio avente per centro a, e i cui punti interni siano tutti punti di A. Allora, per tutti i punti z interni a detto cerchio, f(z) si può rappresentare mediante la serie di potenze:

essendo a_n = f⁽ⁿ⁾(a)/n!. Inversamente, una serie di potenze P(z−a) entro al suo cerchio C di convergenza rappresenta una funzione derivabile (soddisfa alle condizioni di Cauchy-Riemann). Si prenda allora un punto a₁, diverso da a, e interno a C; la P(z−a) sarà sviluppabile in serie di potenze di (z−a₁). Tale sviluppo, che indicheremo con P(z−a/a₁), si dice ‘dedotto immediatamente’ da P(z−a), e il suo cerchio di convergenza C₁ è per lo meno quello di centro a₁, tangente internamente a C. Ma può accadere che C₁ sia maggiore di tale cerchio tangente: che cioè una parte di C₁ sia esterna a C. Nella parte comune a C₁ e a C abbiamo due espressioni a. distinte per la stessa funzione; nella parte interna a C₁, ma esterna a C, la P(z−a/a₁) dà il ‘prolungamento’ o ‘continuazione’ analitica della P(z−a). Iterando questo procedimento si perviene alla definizione di funzione a. (secondo Weierstrass): si chiama a. la funzione definita dall’insieme di tutte le serie di potenze deducibili, per successivi prolungamenti analitici, da una data serie di potenze. Le serie in questione si chiamano gli elementi analitici della funzione a., la quale resta così determinata da uno qualsiasi dei suoi elementi analitici. Il centro del cerchio di convergenza di un elemento analitico è anche detto centro dell’elemento stesso. L’insieme di tutti i punti interni al cerchio di convergenza di almeno uno degli elementi della funzione a. costituisce il campo di esistenza della funzione. Partendo da un dato elemento P(z−a) di una funzione a. si può giungere a un elemento relativo a un qualsiasi punto b del suo campo di esistenza per più vie. Se, qualunque sia la via seguita, si perviene sempre a uno stesso elemento relativo a b, la funzione si chiama uniforme o monodroma (a un sol valore); se, seguendo vie diverse, si ottengono elementi diversi, si chiamerà multiforme o polidroma (a più valori). Sia per la determinazione del campo di esistenza di una funzione a. sia per la classificazione delle funzioni a. è essenziale la considerazione delle loro ‘singolarità’ (poli, punti singolari essenziali) e dei loro ‘zeri’. Per uno dei più importanti teoremi sulle funzioni a. ➔ residuo. La maggior parte delle funzioni di variabile complessa di uso più frequente sono funzioni analitiche.