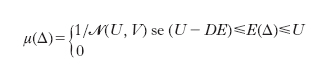insieme

Fisica

Nella meccanica statistica classica con i. statistico, o con il termine ensemble, introdotto da J.W. Gibbs, si indicano famiglie di stati di equilibrio macroscopico. Nello spazio delle fasi, cioè nello spazio delle coordinate p_i, (i=1, 2, 3) e delle quantità di moto q_i (i=1, 2, 3) di ciascuna delle particelle, gli stati microscopici di un sistema di N particelle (identiche, per semplicità) di massa m, contenute in un volume V dato, sono rappresentati da cellette dello spazio di uguale volume (δpδq)^3N; le cellette hanno dimensioni δp e δq rispettivamente in ciascuna delle coordinate di quantità di moto e di posizione, e rappresentano la massima risoluzione con cui gli stati microscopici sono osservabili. L’evoluzione temporale trasforma, in un tempo opportunamente piccolo, la celletta Δ nella celletta Δ′=SΔ, dove S è una trasformazione che verifica le leggi della meccanica newtoniana. Si introduce quindi la nozione di misura di probabilità invariante, o stazionaria, sullo spazio delle fasi, la quale è una funzione che a ogni celletta associa un numero μ(Δ) (misura di Δ) in modo tale che sia: μ(Δ)≥0, Σ_Δμ(Δ)=1, μ(Δ)=μ(SΔ). Si dicono allora i. statistici o ensemble le famiglie di misure stazionarie, che si possono identificare con famiglie di stati di equilibrio macroscopico, interpretando μ(Δ) come la probabilità di trovare il sistema nella celletta Δ eseguendo, in un istante scelto a caso, una misura del suo stato microscopico. Pertanto il valore medio nel tempo, nello stato di equilibrio descritto da μ, di una generica grandezza osservabile f, cioè una generi;ca funzione definita sulle cellette dello spazio delle fasi, si scrive: f̄=Σ_Δμ(Δ)f(Δ). In particolare si possono considerare i seguen;ti valori medi: K(μ)=Σ_Δμ(Δ) T(Δ), energia cinetica; U(μ)=Σ_Δμ(Δ)E(Δ), energia; P(μ)=Σ_Δμ(Δ)P(Δ), pressione; V(μ)=V(Δ)=V, volume; dove T(Δ) e E(Δ) sono, rispettivamente, l’energia cinetica e l’energia totale del sistema quando si trova in uno stato microscopico descritto dalla celletta Δ, mentre P(Δ) è la variazione di quantità di moto per unità di tempo e di superficie, subita dalle particelle di uno stato microscopico contenuto in Δ, nelle collisioni con le pareti del contenitore, cioè P(Δ) è la pressione esercitata sulle pareti del contenitore. Data una famiglia ℰ di misure stazionarie nello spazio degli stati microscopici, a ogni stato microscopico μ ∈ ℰ si possono associare le quantità U, V, K, P (energia, volume, energia cinetica e pressione medie) e ci si può domandare se l’i. statistico ℰ fornisca un modello di termodinamica in cui la temperatura termodinamica T si possa identificare con l’energia cinetica media per particella, a meno di un fattore di proporzionalità da determinare empiricamente e denotato convenzionalmente (2/3 k): T=2K(μ)/3kN. Il significato della locuzione «fornisce un modello di termodinamica» è il seguente: facendo variare μ in ℰ si possono seguire le variazioni di U, V, T, P; se vale la relazione:

[1] (dU+ PdV)/T = differenziale esatto,

allora sarà possibile, integrando la [1], definire una funzione S(μ) su ℰ in modo che fra U, V, S, T, P valgano le relazioni della termodinamica classica in cui S ha la interpretazione di entropia (➔):

[2] (dU+ PdV)/T = dS;

L. Boltzmann chiamò ortodici gli i. statistici che godono della proprietà [2] (proprietà di ortodicità).

Insiemi statistici fondamentali sono quello canonico e quello microcanonico.

L’i. canonico consiste nelle distribuzioni di probabilità sullo spazio degli stati microscopici che hanno a disposizione un volume V; gli elementi μ dipendono da 2 parametri, β>0 e V, tramite la relazione: μ(Δ)=e^−βE(Δ)/Z(β,V), dove Z(β, V)=Σ_Δ e^−βE(Δ) è la somma di partizione canonica (➔ partizione).

L’i. microcanonico consiste nelle misure μ parametrizzate dalle grandezze U e V e definite da:

altrimenti

dove N(U, V), chiamata funzione di partizione microcanonica, è il numero di cellette con energia contenuta nell’intervallo (U−DE, U) e DE è una energia macroscopica, ma molto piccola rispetto a U. In altre parole, nell’i. microcanonico si attribuisce uguale probabilità a tutte le cellette di energia macroscopica U e probabilità nulla alle altre; nell’i. canonico si dà probabilità relativa e^−βU a tutte le cellette di energia macroscopica U, che però può assumere tutti i valori. Boltzmann mostrò che mentre l’i. canonico è ortodico già a volume finito, l’i. microcanonico diviene ortodico solo nel limite termodinamico: N→∞, U→∞, V→∞, in modo che U/N=u,V/N=v restino costanti; è però questo il limite cui si è interessati, vista la grandezza di N nelle applicazioni. Per quest’ultimo i. valgono le famose relazioni

[3] (3/2)kT=K(μ)/N, S(μ)=klogN(U, V);

e per l’altro la temperatura e l’entropia possono essere definite da:

[4] T=2K(μ)/3kN=1/kβ,

S(μ)=−k[βU−logZ(β, V)].

Ciascuno di questi i. fornisce dunque un modello microscopico di termodinamica classica e si può far vedere che, in generale, si ha equivalenza tra le termodinamiche descritte dai due i. se la costante k, che compare nella definizione della temperatura, è la stessa in entrambi gli i. per ogni fissato sistema. Un argomento generale mostra inoltre che k deve essere indipendente dal particolare sistema che si vuole studiare: essa deve essere una costante universale (costante di Boltzmann, pari al rapporto k=R/N tra la costante R che figura nell’equazione di stato dei gas perfetti e il numero N di Avogadro; vale 1,380∙10⁻²³J/K). Poiché l’entropia, la pressione, la temperatura ecc. sono in entrambi i casi esprimibili in termini di due parametri indipendenti (u e v oppure β e v), si è in grado di calcolare l’equazione di stato (cioè il legame fra P, v e T) in termini delle proprietà microscopiche del sistema, almeno in linea di principio: questo è un enorme progresso rispetto alla termodinamica classica, dove l’equazione di stato è una relazione che può essere dedotta unicamente dall’esperienza.

È necessario osservare che le equazioni [3] e [4] sono ottenute usando nel calcolare le somme di partizione da cui si derivano le relazioni termodinamiche, l’approssimazione del continuo: si suppone che le dimensioni delle cellette siano piccole e si sostituisce la somma delle cellette con un integrale nello spazio delle fasi; si commettono così errori trascurabili per temperature sufficientemente alte. Se, invece, non si possono trascurare le dimensioni delle cellette è necessario ricorrere a trattazioni statistiche che tengano conto dei principi della meccanica quantistica (➔ statistica).

Matematica

Generalità

Il termine i. è entrato nell’uso comune nel linguaggio tecnico delle matematiche per esprimere una idea primitiva, cioè irriducibile ad altre idee più semplici, il cui significato può indicarsi non per via di definizione ma per via di intuizione, considerando il termine come sinonimo di aggregato, classe, totalità, collezione di elementi. Anche il termine ‘elemento’ esprime un’idea primitiva: esso è sinonimo di individuo, oggetto, termine ecc. Per indicare che x è elemento dell’i. A si scrive x ∈ A. Un i. si può ritenere definito: a) quando siano assegnati i suoi elementi (per es. l’i. {1, 2, 5, 8} che è costituito appunto dai numeri 1, 2, 5, 8); b) quando sia assegnata una proprietà caratteristica per i suoi elementi (per es.: l’i. dei numeri pari). Mentre nella vita quotidiana si ha occasione di considerare esclusivamente, o quasi, i. contenenti un numero finito di elementi (i. finiti), la matematica si occupa principalmente degli i. contenenti un numero infinito di elementi (i. infiniti: un i. è infinito se, togliendo da esso un numero finito qualunque di elementi, esso continua tuttavia a contenerne). Dal punto di vista logico, occorrerà considerare come due entità distinte un elemento a e l’i. {a} costituito dal solo elemento a, e occorrerà anche prendere in considerazione tra i sottoinsiemi di un i. A, cioè tra gli i. costituiti da una parte degli elementi di A, anche l’i. privo di elementi (i. vuoto, o nullo, indicato correntemente con il simbolo ∅, da considerarsi come contenuto in ogni altro insieme) e, naturalmente, l’insieme A stesso.

Oggi, in accordo con gli orientamenti della matematica moderna, e anche per evitare certe antinomie logiche nel concetto di i., si tende a presentare la teoria degli i. come sistema ipotetico-deduttivo, rinunciando quindi a dare una vera e propria definizione di i., ma caratterizzando tale concetto mediante un certo sistema di postulati relativi alle operazioni da cui può essere generato un insieme.

Teoria degli insiemi

fig. 1, I

fig. 2, I

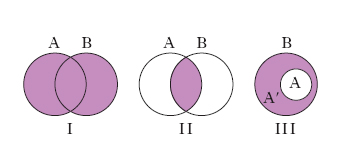
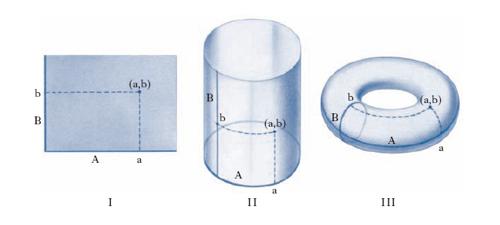
La teoria degli i. è un capitolo relativamente recente della matematica. Tra i suoi grandi creatori o sistematori vi furono G. Cantor (1854-1918) e G. Peano (1858-1932); altri cultori della teoria degli i., oltre a E. Zermelo, furono R. Dedekind, E. Borel, H. Lebesgue, C. de la Vallée Poussin, M. Fréchet, F. Hausdorff, N. Luzin, W. Sierpiński. La teoria generale degli i. può essere considerata, da un punto di vista logico, come il primo capitolo delle matematiche. Potrebbe sembrare, a prima vista, che ben poco vi sia da dire sugli i., intesi come semplici aggregati dei loro elementi (senza introdurre cioè operazioni e relazioni tra gli elementi). Così non è. Esistono, innanzitutto, operazioni generalissime, che possono essere applicate a ogni i., dando luogo a nuovi i., quali: unione (o somma) di due i. A, B, che è l’i. costituito da tutti gli elementi di A e da tutti gli elementi di B (cioè anche: dagli elementi che appartengono ad A o a B); esso si indica con il simbolo A ⋂ B (o anche, qualche volta, A+B). In fig. 1, I è rappresentato l’i. unione dei due cerchi A, B; intersezione (o interferenza o, con termine in disuso, prodotto) di A, B, è l’insieme costituito dagli elementi che appartengono sia ad A sia a B, e si indica con il simbolo A ⋃ B (o anche, talvolta, A∙B). In fig. 1, II è rappresentata l’intersezione dei cerchi A, B. Se A, B sono privi di elementi comuni, l’i. intersezione è l’i. vuoto: A ⋃ B=∅; formazione dell’i. complementare A′ (o, più spesso, ⊂ A o A^⊂) di un i. A rispetto a un i. B: l’i. A′ è dato dagli elementi di B non appartenenti ad A; il caso più frequente è che A sia un sottoinsieme di B (fig. 1, III). Le operazioni di unione e di intersezione tra i. godono delle proprietà: a) commutativa, ossia A ⋂ B=B ⋂ A, A ⋃ B=B ⋃ A; b) associativa, cioè A ⋂ (B ⋂ C)=(A ⋂ B) ⋂ C e A ⋃ (B ⋃ C)=(A ⋃ B) ⋃ C; c) di idempotenza: A ⋂ A=A, A ⋃ A=A; d) distributiva: A ⋂ (B ⋃ C)=(A ⋂ B) ⋃ (A ⋂ C), A ⋃ (B ⋂ C)=(A ⋃ B) ⋂ (A ⋃ C). Inol;tre si hanno le due leggi di De Morgan ⊂ (A ⋂ B)=(⊂ A) ⋃ (⊂ B), ⊂ (A ⋃ B)==(⊂ A) ⋂ (⊂ B) che collegano le operazioni di unione, intersezione e costruzione dell’i. complementare; prodotto (o prodotto cartesiano) di due i. A e B è l’i. i cui elementi sono le coppie di elementi (a, b) con a in A e b in B; l’i. prodotto si indica con A×B, e il suo nome deriva dal fatto che se A e B sono due i. finiti, rispettivamente costituiti da m e n elementi, esso è formato da mn elementi. Se, invece, A e B sono due segmenti (fig. 2, I), A×B è rappresentabile con il rettangolo di lati A, B. Se, poi, A è una circonferenza e B un segmento, A×B è dato dalla superficie laterale di un cilindro (fig. 2, II), infine, se tanto A quanto B sono circonferenze, A×B è la superficie di un toro (fig. 2, III); formazione dell’i. delle parti P(I) di un i. I: è un nuovo i., il quale ha come elementi i sottoinsiemi (o parti di I), cioè gli i. formati da elementi di I. In secondo luogo, si potrà cercare di paragonare fra loro due insiemi A, B, dal punto di vista degli elementi in esso contenuti, cioè dal punto di vista esclusivamente quantitativo. Se A e B sono due sottoinsiemi di un i. I, si dirà che A è contenuto in B (o che B contiene A) se ogni elemento di A appartiene anche a B (si veda ancora la fig. 1, III); tale relazione tra A e B si dice ‘relazione di inclusione’. In simboli: A ⊂ B, B ⊃ A. Talvolta si usa il simbolo ⊂ (o uno analogo) per indicare che A è parte propria di B, cioè che è contenuto in B ma non coincide con esso; per indicare invece che A è contenuto in B senza che si possa escludere che essi coincidano, si usa il simbolo ⊆. Dal punto di vista quantitativo, se A e B sono due i. qualsiasi, si dirà che A e B hanno la stessa potenza (o lo stesso numero cardinale transfinito) se è possibile stabilire una corrispondenza biunivoca fra gli elementi dei due i., cioè se è possibile formulare una legge secondo la quale a ogni elemento di A può essere associato uno e un solo elemento di B e inversamente. Si apre per questa via quell’importantissimo capitolo della teoria generale degli i. che è la teoria dei numeri transfiniti.

Applicazione del metodo assiomatico

Una delle più celebri antinomie che misero in crisi la teoria degli i. di Cantor è quella di B. Russell: secondo tale antinomia l’i. di tutti gli i. che non contengono sé stessi come elemento dovrebbe simultaneamente appartenere e non appartenere a sé stesso. La radice di questo e di altri paradossi fu individuata nell’uso indiscriminato dell’assioma di comprensione, che garantisce per una qualunque proprietà l’esistenza dell’i. degli elementi che godono di essa. Alla difficoltà si cercò di porre rimedio in vari modi; lo stesso Russell elaborò la teoria dei tipi, in cui impose limitazioni all’assioma di comprensione stabilendo una specie di gerarchia, detta appunto dei ‘tipi’, secondo la quale un i. deve essere di tipo superiore a quello dei suoi elementi; non ha quindi più senso parlare di i. appartenenti (o non appartenenti) a sé stessi. E. Zermelo per primo applicò alla teoria degli i. il metodo assiomatico, che ha poi avuto un grande sviluppo; nella sua teoria, l’assioma di comprensione è sostituito da una serie di assiomi di portata più ristretta. Oggi esistono varie e approfondite teorie assiomatiche degli i.; tuttavia esse sono molto più deboli di quella cantoriana, e non permettono nemmeno di dimostrare tramite i soli assiomi corrispondenti a quello di comprensione l’esistenza di i. infiniti; questa deve perciò essere garantita da appositi postulati.

Si espone ora brevemente uno di tali sistemi assiomatici, quello appunto di Zermelo, in una versione modificata e integrata da A. Fraenkel e da T. Skolem; è da rilevare come l’uso del formalismo logico nella teoria degli i., introducendo tutto il rigore che è proprio di tale metodo, contribuisca in maniera essenziale a mettere in luce la difficoltà dei concetti in esame, e insieme la loro fecondità, che sembra portare a sempre nuovi sviluppi. Il tentativo cantoriano di definire esplicitamente la nozione di i. viene così abbandonato; il concetto resta definito implicitamente dagli assiomi. Il linguaggio del sistema contiene gli usuali simboli logici (➔ logica); quale costante specifica contiene il solo predicato binario E dell’appartenenza. Il calcolo è quello dei predicati del I ordine. Gli assiomi caratteristici, come generatori dell’i., sono i seguenti: a) assioma di estensionalità: se gli i. A, B contengono esattamente gli stessi elementi, sono uguali; b) assioma dell’i. coppia: se x e y sono due elementi diversi, allora esiste l’i. che contiene esattamente x e y; c) assioma dell’i. riunione: se A è un i., allora esiste l’i. che contiene esattamente quegli elementi che appartengono ad almeno un elemento di A; d) assioma dell’i. delle parti: dato un i. A, esiste l’i. di tutti e soli i sottoinsiemi di A; e) schema d’assiomi di isolamento: dato un i. A, esiste l’i. degli elementi di A che godono, per una qualunque proprietà definita nel linguaggio formale dato per ogni elemento di A, della proprietà stessa; f) assioma di scelta: dato un i. A, i cui elementi siano a loro volta i. non vuoti e tra loro disgiunti (non aventi cioè elementi comuni), esiste l’i. che ha uno e un solo elemento in comune con ogni elemento di A; g) assioma dell’infinito: esiste l’i. A tale che A contiene l’i. vuoto e, se A contiene un elemento x, contiene anche l’i. che ha x come unico elemento; h) assioma di rimpiazzamento: dati un i. A e una funzione f, esiste l’i. contenente tutti e soli i valori di f per ogni elemento di A; i) assioma di fondazione: dato un i. A non vuoto, A contiene almeno un elemento x tale che nessun elemento di x è anche elemento di A.

Strutture associabili a un insieme

Quando gli i. vengono dotati di ‘strutture’ che permettono di stabilire relazioni od operazioni tra elementi, si abbandona la teoria generale degli i. e si entra nel dominio di teorie più particolareggiate. Così quando si introducano, per gli elementi di un insieme, delle operazioni di tipo algebrico (somma, prodotto o analoghe) si entra nel dominio dell’algebra: gli i. diventano delle strutture algebriche (anelli, corpi, gruppi ecc.). Se invece vengono definite, per gli elementi di un insieme, delle relazioni d’ordine (analoghe alla ordinaria relazione di maggiore e minore per i numeri reali) si hanno le strutture d’ordine a cui fa capo, tra le altre, la teoria dei numeri ordinali transfiniti. Se invece si introduce una relazione di ‘vicinanza’, di ‘intorno’, si hanno le strutture topologiche; gli i. divengono spazi topologici e le loro proprietà sono oggetto della topologia. Queste, che abbiamo nominate, sono le tre strutture fondamentali della matematica moderna, a cui le altre vengono sostanzialmente ricondotte.

I. di punti in uno spazio cartesiano

Particolare interesse presentano gli i. costituiti da punti appartenenti a spazi cartesiani S_n a n dimensioni. Si osservi, però, che lo spazio cartesiano non è puramente e semplicemente l’i. dei punti sopraddetto, ma quell’i. a cui è, inoltre, associata una opportuna struttura di spazio topologico, anzi di spazio metrico (essendo definita una distanza tra due punti qualunque dello spazio).