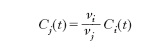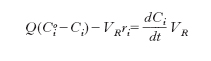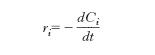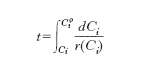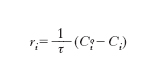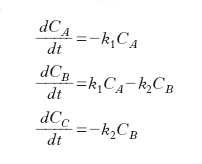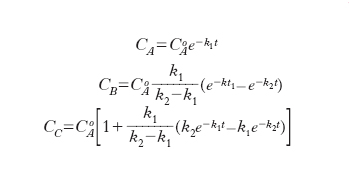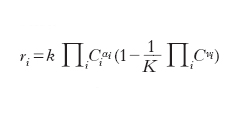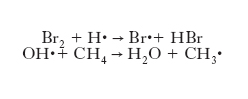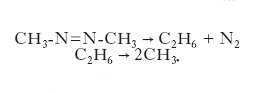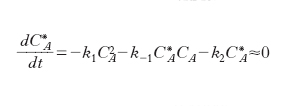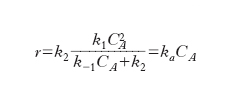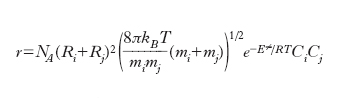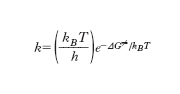cinetica
Parte della meccanica che studia fenomeni di moto, in relazione alla costituzione materiale dei corpi interessati al movimento e alle grandezze (energia cinetica, momenti cinetici ecc.) a essi relative. Può essere considerata come una fase di sviluppo della meccanica, intermedia tra la cinematica e la dinamica.
La c. fisica
La c. fisica studia le velocità con cui avvengono i trasporti di entità (materia, calore, quantità di moto) per effetto di gradienti (➔ trasporto).
In fisica della materia (fisica dei gas, plasmi ecc.) si chiamano cinetiche quelle trattazioni che tengono conto, con opportune tecniche statistiche, del moto dei costituenti elementari del mezzo e la loro distribuzione di velocità, in contrasto con le trattazioni fluide che considerano solo valori macroscopici locali.
La c. chimica
Caratteri generali.- È quella parte della disciplina che si occupa di studiare l’evoluzione nel tempo dei sistemi soggetti a trasformazioni chimiche. Il concetto di velocità di reazione può essere introdotto riferendoci a una reazione, che abbia luogo in fase omogenea, liquida o gassosa, del tipo:
aA+bB+… ⇄mM+nN+ ...
dove A, B, sono le specie reagenti, M,N, i prodotti di reazione e a,b, m,n… i loro coefficienti stechiometrici. Se la miscela dei diversi componenti non si trova in condizioni di equilibrio termodinamico, le loro concentrazioni variano nel tempo, pur rimanendo legate fra di loro dal vincolo imposto dalla stechiometria. Se si sceglie come riferimento un generico componente i la cui concentrazione molare varia secondo la relazione Ci(t), la concentrazione di un’altra specie j si scrive:
dove νi,j indicano i coefficienti stechiometrici di i e j rispettivamente. Ciò premesso si definisce velocità di reazione, e si indica con ri , il numero di moli, o molecole, del componente i che si trasforma per unità di tempo e unità di volume. Essa dipende dalle variabili operative temperatura T e pressione P e dalle concentrazioni delle specie chimiche presenti nella miscela.
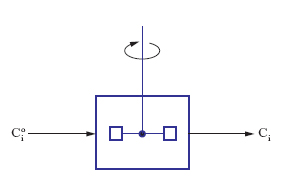
Per illustrarne il significato operativo riferiamoci alla situazione illustrata nella fig. 1 dove un reattore, efficacemente agitato per cui le concentrazioni dei diversi componenti nel suo interno si possano considerare uniformi, viene alimentato da una corrente fluida di portata volumetrica Q, contenente i reagenti a una concentrazione Cio. Se Ci è la corrispondente concentrazione all’uscita dal reattore, un semplice bilancio materiale fornisce la seguente relazione:
dove VR è il volume del reattore. Nel caso il sistema sia chiuso agli scambi di materia, (ovvero Q=0) la precedente diviene:
dalla quale risulta che la velocità di reazione può essere valutata misurando la variazione nel tempo della concentrazione di un reagente e dividendola quindi per il corrispondente intervallo temporale. Se si integra si ottiene:
Il caso più semplice è quello delle reazioni di primo ordine la cui velocità, espressa nella forma ri=kCi , dipende linearmente dalla concentrazione attraverso una costante moltiplicativa k. Se si integra, esplicitando rispetto a Ci si ottiene:
Ci=Cioe−kt
Se viceversa la dipendenza è quadratica del tipo ri=k Ci2, si ottiene:
Entrambe le funzioni precedenti forniscono Cio per t=0, e tendono asintoticamente a zero all’aumentare di t.
Se ci riferiamo ora a un sistema aperto agli scambi di materia con l’esterno che opera in condizioni stazionarie, ovvero tali per cui la dCi/dt=0, la relazione di bilancio diviene:
essendo τ=VR/Q il tempo di residenza medio della miscela nel reattore. Sulla sua base è possibile misurare la velocità di reazione operando in un reattore a flusso. In tutti i casi menzionati risulta quindi che per valutare la costante di velocità di reazione è necessario misurare la concentrazione di un componente presente nella miscela di reazione per tempi diversi e a tale scopo vengono impiegate diverse metodologie analitiche (➔ analisi).
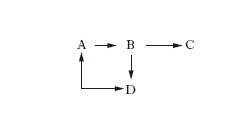
La c. è coinvolta anche nello studio di sistemi complessi di reazioni, nei quali hanno luogo trasformazioni fra di loro interconnesse dove si possono identificare reazioni parallele (fig. 2), se un reagente si trasforma in prodotti diversi, o successive, se uno dei prodotti di reazione subisce una ulteriore trasformazione.
Il più semplice esempio di reazioni successive si può schematizzare come segue:
A → B → C
In un sistema chiuso agli scambi di materia, assumendo che le espressioni cinetiche delle due reazioni siano entrambe di primo ordine con costanti cinetiche k1 e k2 rispettivamente, il bilancio dei 3 componenti presenti nel sistema porta al seguente sistema di equazioni differenziali ordinarie:
la cui integrazione, partendo da una situazione nella quale CoA sia diversa da zero porta alle seguenti espressioni:
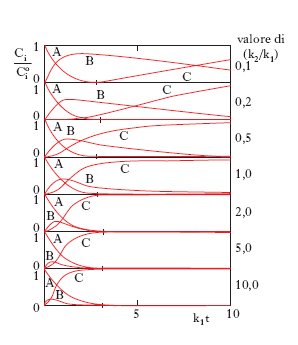
Gli andamenti delle concentrazioni in funzione del tempo sono illustrati nella fig. 3 dalla quale appare che il prodotto A diminuisce nel tempo, la concentrazione del composto intermedio passa per un massimo e tende quindi successivamente a zero mentre il prodotto finale D si accumula continuamente. È interessante osservare che se il rapporto k2/k1 è molto elevato si dimostra facilmente che:
per cui l’intermedio ha una concentrazione piccola proporzionale a quella del reagente. Inoltre poiché in queste condizioni dCB/dt≈0, l’intermedio viene chiamato pseudostazionario.
Espressione generale della velocità di reazione
- È ora importante formulare un’espressione generale della velocità di reazione. Se ci riferiamo a una reazione generale reversibile per cui nella sua evoluzione il sistema tende verso la condizione di equilibrio termodinamico, la dipendenza della velocità di reazione dalle concentrazioni delle specie presenti nel sistema si può scrivere come segue:
L’espressione tra parentesi si annulla quando i valori delle concentrazioni si avvicinano a quelli corrispondenti all’equilibrio termodinamico (K è la costante di equilibrio). Infatti in tali condizioni la velocità di reazione deve essere nulla. L’espressione che precede la parentesi fornisce la dipendenza dalle concentrazioni dei reagenti della velocità della reazione diretta che porta dai reagenti ai prodotti. Essa è detta legge di potenze poiché è espressa dal prodotto delle concentrazioni dei reagenti, ciascuna elevata a un esponente αi. Questi esponenti sono gli ordini di reazione e si valutano dalle informazioni sulla dipendenza, ottenuta sperimentalmente, della velocità di reazione dalla concentrazione dei reagenti. Il parametro k è la costante di velocità di reazione anche se in realtà dipende dalla temperatura attraverso la seguente relazione dovuta ad Arrhenius:
k=Ae−E≠/RT
essendo R la costante dei gas, uguale a 1,98 cal/K mole. E≠ è un parametro chiamato energia di attivazione il cui significato verrà illustrato in seguito; il coefficiente moltiplicativo A è una funzione della temperatura, anche se in prima approssimazione tale dipendenza può essere trascurata. In base all’espressione precedente la k dipende in modo non lineare dalla temperatura secondo un tipico andamento a sigma. Se si considerano reazioni che hanno luogo in fase gassosa, risulta opportuno riferirsi alle pressioni parziali pi dei reagenti invece che alle loro concentrazioni molari. Se il comportamento della miscela gassosa è ideale, le due grandezze sono legate dalla semplice relazione pi=Ci RT per cui le espressioni delle velocità di reazione mantengono la stessa forma salvo un’opportuna ridefinizione della costante di velocità di reazione k.
Ordine e molecolarità di una reazione. - Gli ordini di reazione possono essere interi o frazionari, positivi o negativi, ed esprimono la sensitività della velocità di reazione dalla concentrazione dei reagenti stessi. In realtà i loro valori dipendono dalle condizioni operative. Infatti una reazione chimica avviene solitamente attraverso un insieme di trasformazioni semplici, dette elementari, che riflettono a livello molecolare le interazioni fra le specie in esse coinvolte. In questo caso l’ordine viene chiamato molecolarità e riflette la natura delle interazioni che entrano in gioco fra le molecole che partecipano alla reazione. Per es., una reazione bimolecolare la cui velocità è espressa da:
r=CACB
sottintende che la trasformazione implica una collisione fra le molecole A e B. Rientrano in questa classificazione le reazioni di sostituzione del tipo:
A-B + C → A + B-C
quali:
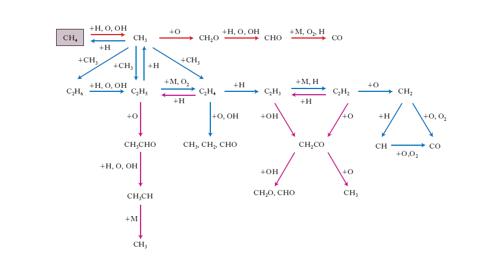
dove il punto indica un elettrone spaiato presente nelle specie radicaliche. A titolo di esempio, si può considerare la combustione del metano che globalmente può essere scritta:
CH4 + 2O2 → CO2 + 2 H2O
e la cui velocità di reazione in prima approssimazione può essere espressa mediante una legge di potenza coinvolgendo i soli reagenti metano e ossigeno. In realtà si tratta di una reazione molto complessa nella quale intervengono diverse reazioni elementari, le principali delle quali sono riassunte nella fig. 4, per cui l’uso di una legge di potenza della velocità riflette solo il comportamento globale di un sistema relativamente complesso.
Reazioni monomolecolari. - Coinvolgono un’unica molecola reagente che isomerizza, come per es. il ciclopropano che si trasforma in propilene, o si dissocia in molecole stabili o radicaliche come si riscontra nei casi seguenti:
È ragionevole ipotizzare che la velocità della reazione sia proporzionale alla concentrazione del reagente, e quindi risulti espressa da un’equazione cinetica del primo ordine. In realtà i valori sperimentali della velocità di reazione in funzione della concentrazione del reagente CA rivelano che tale proporzionalità risulta valida per valori elevati della concentrazione, mentre per valori bassi la velocità è proporzionale al suo quadrato. Per interpretare questo comportamento si deve assumere che la trasformazione avvenga in due stadi, come segue:
A + A ⇄ A* + A
A* → prodotti
In un sistema chiuso il bilancio delle molecole attivate porta alla relazione:
dove k1 e k-1 sono le costanti di velocità diretta e inversa della prima reazione, k2 quella della seconda reazione. Nel passaggio all’ultimo membro si è ragionevolmente ipotizzato che la specie attivata A* si comporti come un intermedio stazionario. Risolvendo l’equazione algebrica rispetto a CA* e sostituendo l’espressione così ottenuta in quella di formazione dei prodotti si ricava:
ka indica una costante apparente di velocità di reazione che per CA elevato tende a (k1/k−1) k2 e la reazione appare di primo ordine mentre per CA basso tende a k1CA e la reazione appare di secondo ordine. Si giustifica pertanto il comportamento riscontrato sperimentalmente.
Reazioni bimolecolari. - Se poniamo l’attenzione su una reazione bimolecolare che avviene in fase gassosa si può assumere che la sua velocità risulti proporzionale al numero di collisioni, per unità di tempo e di volume, che le molecole delle due specie reagenti subiscono. Se si assimilano le molecole stesse a sfere dure di raggio Ri il calcolo si può effettuare attribuendo a esse una velocità media calcolata con la teoria cinetica dei gas. Se inoltre si assume che ogni collisione corrisponda a un evento reattivo, si ricava un’espressione della velocità di reazione che è proporzionale al prodotto delle concentrazioni moltiplicato per un fattore che dipende dalla radice quadrata della temperatura, in disaccordo con l’espressione di Arrhenius. In un approccio più realistico, sempre però assimilando le molecole a sfere dure, si tiene conto della distribuzione delle loro velocità espressa dalla legge di Maxwell, e si assume inoltre che: a) la reazione abbia luogo solo se l’energia cinetica di una molecola rispetto all’altra superi una soglia ε≠. b) la componente di tale energia che contribuisce alla reazione sia quella diretta lungo la linea che passa per i centri delle molecole stesse. Sviluppando questa impostazione si ricava la seguente espressione della velocità di reazione:
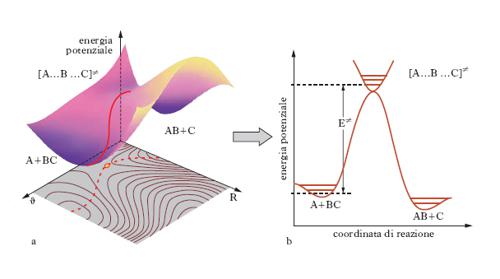
dove mi e mj sono le masse delle due specie, E≠=ε≠NA, kB è la costante di Boltzmann e infine NA è il numero di Avogadro. L’espressione precedente riflette la dipendenza esponenziale dalla temperatura contemplata dalla legge di Arrhenius. Tuttavia se è nota l’energia di attivazione e avendo assegnato valori ragionevoli ai diametri delle sfere che simulano le molecole, si calcola il fattore preesponenziale A e si ottengono dei valori che sono ordini di grandezza superiori di quelli sperimentali. Le ragioni di tale disaccordo risiedono nel fatto che non tutta l’energia cinetica che le molecole si scambiano nella collisione contribuisce al superamento della soglia critica di energia ε≠ poiché parte di essa viene dissipata nei moti interni vibrazionali e rotazionali delle molecole stesse. Infatti tale disaccordo è tanto più pronunciato quanto maggiore è la complessità delle molecole in gioco e quindi la possibilità di disperdere energia nei moti interni. Per superare questa difficoltà è necessario tenere conto che su scala molecolare la reazione chimica avviene attraverso la rottura e la formazione di legami fra gli atomi presenti rispettivamente nei reagenti e nei prodotti di reazione. La trasformazione può essere descritta mediante una tipica superficie che fornisce l’energia potenziale del sistema in funzione delle distanze fra gli atomi direttamente coinvolti. Queste superfici indicate con PES (potential energy surface) hanno il tipico andamento illustrato nella fig. 5, per una reazione di sostituzione nella quale l’atomo B viene trasferito dalla molecola B-C alla molecola A-B e il passaggio dai prodotti ai reagenti è descritto dalla linea rossa il cui percorso viene chiamato cammino di reazione. La dinamica della collisione può essere studiata descrivendo il moto del punto che rappresenta il sistema molecolare reagente sulla PES. Affinché la reazione abbia luogo è necessario che venga superata la barriera di energia potenziale E≠ e perché ciò si verifichi è necessario che l’energia delle molecole reagenti sia sufficientemente elevata. Alternativamente il calcolo può essere affrontato mediante la termodinamica statistica tenendo conto che il flusso medio dei reagenti che attraversa una particolare zona della PES alla sommità della barriera porti ai prodotti di reazione. In questa impostazione si ricava che la costante k è espressa da:
dove kB è la costante di Boltzmann e ħ quella di Planck, mentre ΔG≠ è la variazione di energia libera relativa al passaggio dai reagenti allo stato di transizione che costituisce il complesso molecolare instabile che si trova alla sommità della barriera di energia potenziale. Malgrado la sua esistenza sia effimera poiché ha una vita media di 10−12−10−11 s, dall’andamento della PES alla sommità della barriera si possono calcolare le sue caratteristiche geometriche e le frequenze di vibrazione degli atomi, indispensabili per calcolare la ΔG≠. Grazie alle conoscenze accumulate nel settore della spettroscopia molecolare e ai recenti progressi raggiunti in quello della chimica computazionale (➔) è attualmente possibile valutare con accuratezza i dati necessari per calcolare con la relazione precedente la costante di velocità di reazione. Sebbene originariamente concepita per reazioni in fase gassosa, la teoria dello stato di transizione è stata applicata con successo anche alle reazioni che hanno luogo in soluzioni liquide.