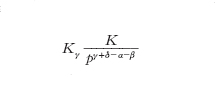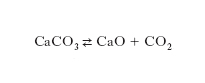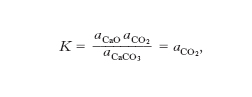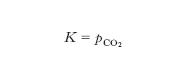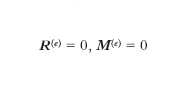equilibrio
Astronomia
E. stellare Condizione fisica di una stella (➔), in cui tutta l’energia generata nella parte centrale sia trasmessa agli strati superficiali e da questi irradiata all’esterno. Nello studio della costituzione interna delle stelle si seguono due indirizzi a seconda che si supponga che l’energia sia trasmessa attraverso la stella per convezione oppure per irraggiamento ( teoria dell’e. convettivo e dell’e. radiativo). Le due teorie sono associabili, supponendo il nucleo centrale in e. convettivo e l’inviluppo esterno gassoso, che costituisce la parte maggiore dell’astro, in e. radiativo.
Biologia
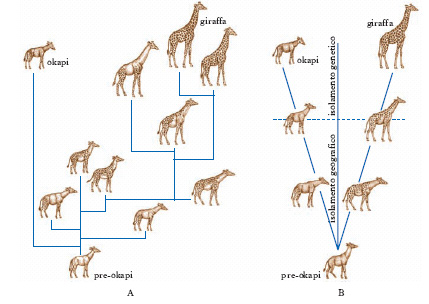
In paleontologia, la teoria degli e. intermittenti (punctuated equilibria; fig. 1), proposta nel 1972 dai paleontologi statunitensi N. Eldredge e S.J. Gould, poi sostenuta e sviluppata da S.M. Stanley, si basa sul modello di speciazione peripatrica proposto da E. Mayr nel 1954 (➔ speciazione), in base al quale la speciazione per principio del fondatore è il contesto in cui avviene buona parte dell’evoluzione. Secondo la teoria degli e. intermittenti, la storia evolutiva consiste in lunghi periodi in cui le specie sono relativamente stabili perché l’evoluzione è ridotta o assente. Questi periodi sono definiti intermittenti, poiché possono essere interrotti da brevi periodi caratterizzati da rapida evoluzione e comparsa di nuove specie. Per spiegare questo modello, Eldredge e Gould ipotizzano che la maggior parte dei cambiamenti avvenga rapidamente in piccole popolazioni locali, in concomitanza con l’acquisizione dell’isolamento riproduttivo. La teoria include quindi i processi tradizionali neodarwinisti dell’evoluzione graduale: all’interno di popolazioni in corso di speciazione, i caratteri si modificano gradualmente, benché rapidamente, sotto l’influenza della deriva genetica e della selezione individuale. L’evoluzione avviene in modo così rapido e in un’area geografica così localizzata che soltanto raramente potrà essere ben documentata dai reperti fossili. Questa nuova unità, geneticamente isolata, può coesistere con la specie originaria e non necessariamente sostituirla. Raggiunto l’isolamento riproduttivo, la nuova forma si espande dal proprio sito di origine, divenendo sufficientemente abbondante e diffusa da essere ritrovata nei reperti fossili. Le testimonianze fossili provengono quindi in prevalenza dai periodi di stasi, mentre pochi sono i fossili dei periodi di rapido cambiamento.
In genetica di popolazioni, l’ e. di Hardy-Weinberg rappresenta la stabilità delle frequenze geniche in una popolazione e si può enunciare con il seguente teorema: se p e q (con p=1−q) sono le frequenze di due alleli A e a presenti in una popolazione, queste restano invariate nelle generazioni successive se nella popolazione: a) la frequenza di mutazione A → a è uguale a quella a → A; b) non si rileva migrazione differenziale di uno dei due alleli da e verso l’esterno; c) nessuno dei tre genotipi possibili (AA, Aa e aa) è avvantaggiato rispetto agli altri; d) se la popolazione è indefinitamente grande.
Chimica
E. fisico e chimico
Stato di un sistema chimico caratterizzato dalla costanza dei parametri che lo definiscono, in particolare la pressione, la temperatura e la sua composizione. Lo studio degli stati di e. rientra nel dominio della termodinamica classica. Si consideri, in prima istanza il comportamento di un sistema a più componenti, nel quale a temperatura e pressione assegnate siano presenti una fase liquida e una fase vapore fra le quali si distribuiscano i diversi componenti. La condizione di e. termodinamico è espressa dalla condizione:
in cui G è l’energia libera o potenziale termodinamico di Gibbs. Questa condizione va unita all’altra: dT=0, che esprime l’e. termico del sistema, con T temperatura assoluta, e all’altra ancora: dP=0, che definisce l’equilibrio meccanico, essendo P la pressione. L’energia libera è una grandezza estensiva che dipende dalla temperatura, dalla pressione e dal numero di moli di tutti i componenti costituenti il sistema materiale; questo nel caso più generale è eterogeneo, cioè è formato da più fasi. Pertanto:
con riferimento a un sistema costituito da c componenti e f fasi; nij è il numero di moli del componente i-esimo presenti nella fase j-esima, μij è il corrispondente potenziale chimico (energia libera parziale molare) definito dalla relazione:
dove R è la costante dei gas e f̅ij è la fugacità. La [1], tenendo conto della [2] e dell’equazione di Gibbs-Duhem
(∑
(∑ci=1 ∑fj=1 μijdnij=0)
assume l’espressione più esplicita:
[
]
Dalla [4] si possono derivare tutte le proprietà termodinamiche degli stati di equilibrio. In un sistema omogeneo (formato cioè da una sola fase), soggetto soltanto a trasformazioni fisiche, si ha dni=0 per tutti i componenti, in quanto il numero di moli di ogni componente deve rimanere costante, e quindi la [4] è certamente soddisfatta. Quindi, in un sistema omogeneo, come, per es., una soluzione liquida o una miscela di gas, se tra i componenti non possono avvenire reazioni chimiche, si ha costantemente l’equilibrio. Quando l’e. termodinamico è riferito a sistemi eterogenei, la natura chimica dei componenti può non essere modificata ( e. tra le fasi), oppure possono intervenire reazioni chimiche ( e. chimico).
E. tra le fasi
Nell’ipotesi di assenza di reazioni chimiche, il numero di moli di un componente, comunque ripartito tra le varie fasi, deve rimanere costante. Si ha perciò la condizione ∑f1 jdnij=0. Questa e la [4] per essere simultaneamente soddisfatte richiedono che sia μi1=μi2=μi3=…=μif: si ha cioè l’importante proprietà che per un sistema in e., il potenziale chimico di ciascun componente deve essere lo stesso in ogni fase; inoltre, in base alla definizione del potenziale chimico [3] la stessa proprietà vale per la fugacità f dei vari componenti in ogni fase: f̅i1=f̅i2=…=f̅if. Dall’uguaglianza sopra ricavata, esprimendo in forma opportuna il potenziale chimico, si possono ottenere tutte le relazioni quantitative riguardanti gli e. tra le fasi: liquido-liquido, liquido-vapore, liquido-gas, liquido-solido, gas-solido ecc. Ricordando che, in generale, il potenziale chimico è funzione della pressione, della temperatura e della composizione, la proprietà sopra dimostrata corrisponde a scrivere (f−1) relazioni per ogni componente, quindi complessivamente c(f−1) relazioni. Aggiungendo altre eventuali relazioni che possono essere imposte al sistema, sotto forma di r equazioni tra le variabili di stato, si ha che le equazioni risolutive sono in numero di c(f−1)+r. Le incognite, cioè i parametri che definiscono il sistema, sono 2 (pressione e temperatura) oltre ai parametri di composizione, che sono c−1 in ogni fase, quindi complessivamente f (c−1)+2. Se il numero delle equazioni è uguale a quello delle incognite, il sistema si trova in uno stato univocamente definito, mentre se il primo è minore del secondo, possono assegnarsi arbitrariamente dei valori a un certo numero di parametri di stato, numero precisamente pari alla differenza tra le incognite e le equazioni, e al quale si dà il nome di varianza, o grado di libertà,
V = c + 2 − f − r.
Questa relazione prende il nome di regola delle fasi (o di Gibbs): essa dà il numero di parametri di stato che si possono far variare senza turbare l’e. del sistema e quindi senza cambiare il numero e la natura delle fasi presenti. A seconda che la varianza valga 0, 1, 2 ecc., il sistema si dice invariabile, mono-, bivariante ecc. Per es., nel caso di due componenti e due fasi (liquido e vapore) con r=0, si ha V=2 (sistema bivariante), quindi possono fissarsi due soli parametri (per es., pressione e composizione) e il terzo (la temperatura T) ne deriva per conseguenza. Se invece fosse presente un azeotropo, si dovrebbe aggiungere un’equazione di restrizione (uguaglianza delle composizioni nelle due fasi), quindi si avrebbe r=1 e la varianza si ridurrebbe a 1 (sistema monovariante): in tal caso solo un parametro può essere fissato ad arbitrio (per es., la pressione), mentre gli altri due conseguirebbero da esso. Per un sistema costituito da due fasi liquide e una fase vapore, sempre nel caso di due componenti, si troverebbe V=1; anche in questo caso solo un parametro si può fissare ad arbitrio (per un approfondimento sugli e. in sistemi polifasici a più componenti ➔ diagramma).
Nell’analisi delle condizioni di e. di un sistema soggetto a una trasformazione chimica è opportuno soffermare in prima istanza l’attenzione sui sistemi omogenei fra i cui componenti può aver luogo una generica reazione chimica del tipo: αA+βB ⇄ γC+δD, dove A e B sono i reagenti, C e D i prodotti, mentre α, β, γ e δ sono i coefficienti stechiometrici. Si supponga che la reazione avvenga isotermicamente alla generica temperatura T. Detto ξ il grado di avanzamento della reazione rispetto ad A, si calcolano i numeri di moli in forma differenziale (nA0 è il numero iniziale di moli di A):
sostituendo questi valori nella [4] e dovendo essere dξ≠0, si trova la condizione:
che costituisce un’ulteriore relazione tra i potenziali chimici dei componenti. Se nella [5] si sostituisce al potenziale chimico la sua espressione in funzione dell’attività del componente considerato, si perviene al risultato:
dove ΔGT* è la variazione di energia libera della reazione fatta avvenire alla temperatura T e in modo che sia i reagenti che i prodotti si trovino nello stato assunto come riferimento per il calcolo delle attività nel caso degli e. chimici; R è la costante dei gas e K è la costante di e.,
in cui a indica l’attività di ogni componente. Il valore assunto da ΔGT* consente di valutare orientativamente le possibilità di pratica realizzazione di una reazione: se ΔGT* è 〈0, la reazione è realizzabile; se ΔGT* è >40.000 kJ/kmol la reazione non può trovare applicazione (salvo casi eccezionali); nel caso intermedio, 0〈 ΔGT* 〈40.000 kJ/kmol, la possibilità di realizzazione industriale della reazione è di difficile attuazione, ma non è esclusa a priori. Nel caso di reazioni gassose l’attività di ogni componente diventa numericamente uguale alla sua fugacità espressa in bar e, se si aggiunge l’ipotesi che il valore della pressione totale alla quale avviene la reazione sia basso, il coefficiente di fugacità è, in pratica, unitario, e la fugacità viene a coincidere con la pressione parziale; per cui la [7] si può scrivere:
dove p indica la pressione parziale, P la pressione totale e y la frazione molare dei singoli componenti nella fase gassosa. Nel caso di reazione in fase liquida, si preferisce sostituire l’attività con il prodotto della frazione molare x per il rispettivo coefficiente di attività. Indicando con Kγ il termine dipendente dai coefficienti di attività, la [7] si può scrivere:
Le [8] e [9] permettono di studiare l’influenza dei vari parametri di e.; esse inoltre, esprimendo le frazioni molari in funzione del numero di moli iniziali e del grado di avanzamento ξ della reazione, permettono di calcolare la composizione di e. della miscela in reazione. La dipendenza di K dalla temperatura è data dalla cosiddetta isocora di van’t Hoff: K aumenta o diminuisce all’aumentare della temperatura, a seconda che la reazione sia endotermica o esotermica. È poi evidente dalle [7], [8] e [9] che, se K aumenta, deve aumentare la concentrazione dei prodotti di reazione (C, D) e diminuire quella dei reagenti (A, B). Perciò, una temperatura alta favorisce la reazione soltanto nel caso in cui essa sia endotermica, mentre la ostacola nel caso contrario. L’influenza della pressione, sensibile soltanto nelle reazioni che avvengono in fase gassosa, risulta dalla [8] espressa nella forma:
la reazione è quindi favorita da un aumento di pressione soltanto se α + β > γ + δ, cioè se avviene con diminuzione di volume. Un eccesso di reagenti, in quanto comporta un aumento del denominatore della [8] o della [9], favorisce la reazione, mentre la presenza di prodotti di reazione in misura maggiore di quella che deriva dalla combinazione dei reagenti ostacola la reazione. La presenza di eventuali gas inerti ha un effetto analogo a quello di una riduzione della pressione ed è quindi vantaggioso soltanto se la reazione avviene con un aumento di volume. Si noti infine che ogni reazione è caratterizzata da una propria costante di e.; però, se tale costante ha un valore molto elevato, come, per es., avviene nelle reazioni di combustione, ai fini pratici è come se detta reazione avvenisse completamente. Perciò nello scrivere una reazione si usa la doppia freccia ⇄ quando la conversione è soltanto parziale e invece una freccia semplice quando si ha una conversione praticamente totale: H2+I2 ⇄ 2HI; H2+Cl2 → 2HCl. L’influenza esercitata dai vari parametri di e. sull’andamento di una trasformazione determinabile quantitativamente in base a considerazioni termodinamiche era già stata espressa qualitativamente nel principio dell’e. mobile (principio di Le Châtelier-Braun), secondo il quale ogni sistema in e. chimico, per alterazione di uno dei parametri di e., subisce una trasformazione tale che, da sola, produrrebbe un’alterazione di segno contrario dello stesso parametro.
In chimica analitica, le costanti di e. prendono il nome in funzione della grandezza sotto cui compaiono le specie chimiche che partecipano all’e.; così si parla di costante di attività (funzione soltanto della temperatura) e di costante di concentrazione (funzione della temperatura e della forza ionica). Le costanti miste sono costanti che vengono definite per gli e. ai quali partecipa lo ione idrogeno: in tale tipo di costante questo ione viene espresso in termini di attività, vista la possibilità di determinarla con una misura di pH, e le altre specie in termini di concentrazione. Le costanti condizionali, infine, sono grandezze che variano a seconda del mezzo nel quale sono considerate e che tengono conto di eventuali reazioni collaterali.
Per i sistemi eterogenei nei quali sono presenti più fasi, si aggiunge a quelle già considerate anche l’equazione [5] che può essere riguardata come un’equazione di restrizione dovuta alla reazione chimica. Se si hanno più reazioni indipendenti tra i componenti del sistema, si ottengono altrettante equazioni come la [5] e il numero delle restrizioni aumenta. Dal punto di vista quantitativo, lo studio dell’e. in un sistema eterogeneo, sede di reazioni chimiche, si esegue analogamente a quanto si fa per i sistemi omogenei, tenendo conto delle relazioni per l’e. tra le fasi insieme a quelle proprie delle reazioni chimiche. La condizione di uguaglianza della fugacità di ciascun componente in ogni fase, scegliendo le stesse fugacità di riferimento, può esprimersi anche come uguaglianza delle attività: in tal caso la [7] può pensarsi riferita a una qualunque delle fasi presenti. Esistono naturalmente anche delle condizioni semplificative: per es., per la decomposizione del carbonato di calcio secondo la reazione:
CaCO3 ⇄ CaO + CO2,
si hanno due fasi solide (immiscibili) e una fase gassosa; potendosi con buona approssimazione assumere uguale a 1 l’attività delle fasi solide, la costante di e. diviene:
aCaO aCO2
K = −−−−−−−− = aCO2,
aCaCO3
e, per pressioni non elevate,
K = pCO2:
in tal caso il valore di K è determinato soltanto dalla pressione parziale dell’anidride carbonica proveniente dalla decomposizione del carbonato di calcio.
Ecologia
Ogni essere vivente è un componente della comunità vegetale e animale in cui si trova, che entra in relazione con gli altri esseri del medesimo ambiente biologico: relazioni ora antagonistiche, ora mutualistiche, le quali continuamente ne favoriscono o ne minacciano il benessere o addirittura l’esistenza. Si stabilisce così un e. ecologico che si conserva per un periodo più o meno lungo, in un dato ambiente. L’apparente stabilità è il risultato di continue variazioni numeriche dei vari componenti della comunità. Per es., generalmente il numero degli erbivori e quello dei carnivori di una data località rimane a lungo costante, ma ciò avviene in conseguenza di una continua oscillazione numerica dei due gruppi di organismi: se aumenta il numero dei carnivori, aumenta la loro pressione di predazione sugli erbivori, d’altra parte non appena gli erbivori diminuiscono oltre una certa misura, i carnivori, per la carenza di prede, declinano progressivamente di numero. Lo stesso accade nelle relazioni fra parassiti e ospiti. Quando in un determinato ambiente o territorio sono rappresentati tutti i gruppi di consumatori e di regolatori del consumo, si stabilisce l’e. ecologico; quando circostanze esterne producono la scomparsa o la diminuzione eccessiva di uno dei suoi elementi, tutto il sistema ne risente, subendo un danno talvolta irreparabile. Così, l’introduzione di nuove specie animali in un dato territorio (per es., coniglio in Australia, passero negli USA, cani, gatti e volpi nella Nuova Zelanda ecc.) ha provocato spesso gravissimi danni alla flora o alla fauna locale.
Economia
E. economico
Ogni configurazione economica che rappresenta una situazione dalla quale non vi è incentivo a muoversi. Tipico è l’incontro sul mercato della domanda e dell’offerta, che stabilisce il prezzo (di e.) al quale le merci verranno scambiate. Dal punto di vista dell’e. economico generale, questo si definisce come posizione nella quale, date determinate condizioni iniziali, un individuo o una collettività agenti come enti economici possono realizzare il massimo di utilità soggettiva (e che quindi l’individuo e la collettività tendono a raggiungere o a ripristinare). L’ e. parziale analizza posizioni di e. in un dato mercato, date le condizioni che vigono sui restanti mercati. Quando invece tutti i mercati vengono presi simultaneamente in considerazione, si parla di e. economico generale, la cui formulazione risale a L. Walras e V. Pareto. Premessa di queste teorie è l’invariabilità delle condizioni iniziali (gusti individuali formalizzati dalle ‘curve di indifferenza’, disponibilità dei beni, stato della tecnica produttiva); si tratta quindi sempre di un e. statico, relativo a un dato momento, mentre la realtà è essenzialmente dinamica anche nelle società più semplici e meno mutevoli. Per questo, e per l’intervento di impulsi e forze extraeconomiche nel determinare le azioni umane, la nozione teorica di e. economico, pur non trovando corrispondenza precisa nella realtà concreta, ha costituito uno strumento concettuale che ha svolto una funzione cruciale nello sviluppo rigoroso dell’analisi economica.
E. parziale
I problemi di e. parziale più frequentemente studiati dalla scuola classica sono quelli relativi al valore e prezzo dei beni, al valore e distribuzione della moneta, ai rapporti di scambio internazionale, al livello dei salari, al tasso dei profitti, salvo poche eccezioni (F. Ferrara, T. Martello), senza rilevarne le mutue dipendenze. È infatti soltanto con la scuola matematica che i rapporti di interdipendenza dei fenomeni economici trovano la loro rigorosa espressione (in particolare con A. Cournot, per il monopolio, e con H.H. Gossen, per il rapporto tra sacrificio e utilità del lavoro). A opera di questa scuola e, contemporaneamente, ma indipendentemente, di W.S. Jevons, di L. Walras e di K. Menger, l’indagine si polarizza sulla ricerca di un sistema di equazioni in cui i prezzi dei beni e le quantità scambiate figurano come incognite, mentre le utilità soggettive dei beni scambiati e le quantità inizialmente possedute dagli scambisti si considerano note. In tale indagine assume importanza essenziale l’utilità marginale, e il teorema dell’uguaglianza delle utilità marginali ponderate diviene la chiave della scienza economica. A una successiva e sempre maggiore estensione della teoria degli e. parziali hanno contribuito, tra gli altri: E. Barone e M. Pantaleoni, in Italia; F.Y. Edgeworth e A. Marshall, in Inghilterra; R. Auspitz e R. Lieben, in Austria; I. Fisher in America.
E. statico generale
L’unità del processo economico e la tendenza a un solo e., che sia insieme e. del produttore, del consumatore, del risparmiatore, del lavoratore ecc., è stata studiata da Walras, che ne ha fissato le equazioni nell’ipotesi di libera concorrenza, dimostrando come il numero delle condizioni sia uguale al numero delle incognite e l’e. sia quindi determinato. La formulazione definitiva dell’ e. statico generale è però quella data da Pareto, sulla base della rappresentazione di Walras ampliata in modo da considerare anche l’ipotesi del monopolio e i fenomeni di rendita o di passaggio da un e. all’altro; con essa, superate le distinzioni tra produzione, distribuzione, consumo e scambio, l’economia pura si riduce allo studio sintetico dei gusti da cui sono mosse le azioni umane (determinabili in via induttiva con l’analisi delle scelte) e degli ostacoli che vincolano le azioni stesse (limitazione dei beni, costi di produzione, stato della tecnica, regime giuridico). Tra i contributi all’analisi dell’e. generale vanno segnalati quelli di K. Wicksell, J.B. Clark, H.L. Moore, gli apporti di matematici ed economisti quali A. Wald, J.L. von Neumann, L. Amoroso, R. Frisch ecc.
Interesse particolare, non disgiunto da critiche, ha suscitato la teoria di J.M. Keynes che, sulla base di un sistema essenzialmente statico di tre equazioni e una identità, contesta le conclusioni delle scuole precedenti e, implicitamente, anche di Walras e Pareto circa gli e. economici e la loro tendenza, in caso di perturbazione, a ripristinarsi con spontanei aggiustamenti dei prezzi, delle retribuzioni ai fattori produttivi e della loro allocazione, senza che si produca la disoccupazione dei fattori stessi. Secondo J.M. Keynes, il sistema economico, una volta allontanatosi sensibilmente da una posizione d’e., tende a distaccarsene sempre di più e a raggiungere, soprattutto attraverso mutamenti del reddito sociale, una nuova posizione di e. ‘di sottoccupazione’, accompagnata cioè da una persistente inutilizzazione dei fattori produttivi (risorse umane e materiali). Gli e. di piena occupazione sono anzi per la scuola keynesiana l’eccezione e non la regola e tocca allo Stato intervenire, promuovendo gli investimen;ti o i consumi, per far ritornare il sistema a un e. di piena occupazione o per mantenervelo.
Conseguenze assai rilevanti per la teoria dell’e. economico generale ha avuto, d’altra parte, la critica di P. Sraffa all’ipotesi concorrenziale (il mercato omogeneo di libera concorrenza finisce per avere un suo mercato particolare, il prezzo quindi non è più un dato per le singole imprese ma una funzione decrescente delle loro vendite) e su questa base J. Robinson ed E.H. Chamberlin hanno tentato di dimostrare la possibilità di un e. per forme di mercato intermedie tra la concorrenza perfetta e il monopolio.
Il largo impiego dello strumento matematico che caratterizza l’analisi economica degli anni successivi ha permesso poi a J.R. Hicks di riprendere e perfezionare la teoria di Walras e di Pareto, preoccupandosi soprattutto di risolvere il problema della stabilità dell’e. economico generale, e O. Lange e P.A. Samuelson ne hanno proseguito la ricerca.
E. dinamico
Il crescente interesse per i problemi di sviluppo ha indotto contemporaneamente a uscire dall’impostazione walrasiana e a occuparsi, anziché del mantenimento della configurazione raggiunta da un sistema, della sua evoluzione nel tempo e ne è derivata un’abbondante varietà di modelli macroeconomici, di derivazione keynesiana, in cui si mira alla soluzione di problemi di e. dinamico di breve e di lungo periodo. Un tentativo per applicare la teoria dell’e. generale allo studio empirico delle correlazioni esistenti tra i vari settori dell’economia nazionale è stato poi fatto da W. Leontief con il suo schema (input-output analysis) che ha pure suscitato fervore di teoriche e di pratiche attuazioni. Negli sviluppi successivi, la teoria dell’e., mentre da un lato ha trovato formulazioni matematiche sempre più complesse (A. Wald, K.J. Arrow, G. Debreu ecc.) volte a dare una formulazione dinamica dell’e. e a considerare le decisioni degli operatori economici in condizioni di incertezza sul futuro, ha, nel contempo, formato oggetto di nuove insorgenze critiche, soprattutto da parte di coloro (come J. Kornai in Anti-Equilibrium, 1971) che sottolineano i sistemi di informazione, di reazioni e di adattamento del meccanismo economico, che non si manifestano nell’operare dei prezzi, ma con regole, messaggi e controlli di tipo diverso, da cui si prescinde nelle concezioni generali di equilibrio.
La letteratura economica ha posto particolare attenzione ai cosiddetti modelli monetari di e. economico generale (D. Patinkin, R.W. Clower, F. Hahn e A. Leijonhufvud). Proprio partendo da alcuni spunti dell’analisi teorica di questi economisti, nella quale l’esistenza della moneta quale mezzo di scambio altera alcuni postulati essenziali del modello di e. economico generale, sono stati sviluppati nuovi modelli detti di disequilibrio, nei quali la rigidità di alcune variabili (prezzi, salari) fa sì che gli scambi e i processi di aggiustamento nei mercati si realizzino anche in situazioni diverse da quelle dell’e. economico previsto dalla teoria di Walras.
E. e modelli matematici
Lo sviluppo della modellistica matematica applicata all’economia ha arricchito il concetto di e., e in particolare di e. dinamico. I contributi enfatizzano infatti la presenza di una molteplicità di e. economici caratterizzati da diverse condizioni iniziali dell’economia. Negli sviluppi più complessi, tale molteplicità di e. non consente di determinare, a priori, verso quale e. l’economia stia convergendo ( indeterminatezza degli e.).
Fisica
E. meccanico
L’e. meccanico di un corpo si distingue in statico e dinamico. L’ e. statico (o semplicemente e.) si ha quando il corpo è fermo. Un corpo puntiforme è in e. statico quando, essendo inizialmente in quiete, non è assoggettato a forze, oppure queste hanno risultante nullo (R = 0 equazione fondamentale della statica del punto). Per un punto soggetto a determinate forze, questa circostanza dell’annullarsi del risultante (da valutarsi in corrispondenza a velocità nulla del punto) in genere si può verificare soltanto in certe posizioni del punto stesso, dette posizioni di e.: un punto potrà quindi essere in e. soltanto se si trova in una posizione di e. con velocità nulla (il solo fatto di trovarsi a passare per una di tali posizioni evidentemente non basta ad assicurare l’e.: si pensi, per es., a una massa pendolare oscillante intorno alla sua posizione di e.). Per un corpo che non sia assimilabile a un punto, esclusa la convenienza o addirittura la possibilità di un esame dell’e. di ciascuno dei punti costituenti il sistema, si cerca di ricorrere a condizioni globali per lo studio dell’e. almeno in senso macroscopico. Se il sistema è in quiete, devono essere sempre soddisfatte le cosiddette equazioni cardinali della statica, esprimenti l’annullarsi del risultante R(e) e del momento risultante M(e) delle forze esterne:
Queste condizioni, sempre necessarie, generalmente non bastano ad assicurare l’e., anche se si aggiunge la condizione che inizialmente tutti i punti del sistema siano in quiete (si pensi, per es., a due palline, ciascuna sottoposta a una forza uguale e contraria all’altra: l’insieme delle due forze è equilibrato, ma sotto la loro azione ciascuna delle due palline, anche se inizialmente ferma, prende a muoversi). Fa eccezione il caso, molto importante, dei sistemi rigidi: un sistema rigido inizialmente in quiete, sottoposto a forze esterne nel loro complesso equilibrate, permane nella quiete. La definizione di configurazione di e. è analoga a quella già data per il punto; è tale ogni configurazione in corrispondenza alla quale l’insieme delle forze esterne (valutate per velocità nulla) riesce equilibrato.
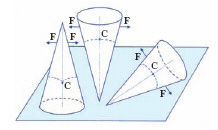
Approfondendo l’indagine sull’e. di un corpo si è portati a riconoscere che possono darsi tre diversi tipi di e.: stabile, instabile, indifferente (fig.2). Una posizione di e. è stabile o instabile a seconda che, perturbando leggermente le condizioni del corpo, esso tenda o no a ritornare nella posizione di partenza; si parla invece di e. indifferente quando ogni possibile posizione del corpo è di e., sicché una eventuale perturbazione, a partire da una di esse, non fa che portarlo in un’altra posizione di equilibrio. Un’impostazione sintetica ed efficace dei problemi di e. si realizza attraverso il principio dei lavori virtuali (➔ lavoro).
La locuzione e. dinamico può riferirsi a due diverse condizioni dinamiche. Per un corpo puntiforme può in primo luogo parlarsi di e. dinamico quando il punto, inizialmente in movimento, viene assoggettato a forze a risultante nullo: l’accelerazione si annulla identicamente, la velocità resta vettorialmente costante, il punto si muove di moto rettilineo uniforme: è la seconda delle due eventualità previste dal principio d’inerzia. Ma si può parlare di un e. dinamico anche quando, sia o no il punto inizialmente in quiete, esso viene sottoposto a forze a risultante non nullo: si ha allora, a norma dell’equazione fondamentale della meccanica, F=m a, un’accelerazione e quindi una forza d’inerzia (−m a), che, si può dire, equilibra le forze effettive. I due casi si compendiano in sostanza nel principio di d’Alembert: «durante il moto la forza attiva, la forza vincolare e la forza d’inerzia devono farsi e.»; il primo caso poi corrisponde all’ipotesi che la forza attiva e la forza vincolare si facciano, per loro conto, e. e venga quindi a mancare la forza d’inerzia, onde il punto si muove ‘per inerzia’. E. radioattivo Una sostanza radioattiva a si dice in e. con un prodotto b della sua disintegrazione, ancora radioattivo, quando il rapporto fra le quantità delle due sostanze rimane, almeno sensibilmente, costante (quando cioè il numero degli atomi di a e quello degli atomi di b che si disintegrano in 1 s sono uguali). E. statistico In meccanica statistica, l’insieme di un numero grandissimo di sistemi indistinguibili l’uno dall’altro per le loro proprietà (per es., le molecole di un gas) si dice in e. statistico se resta costante da istante a istante il numero di sistemi (non sempre gli stessi in generale) che si trovano in un determinato stato. E. termico Un sistema è in e. termico quando non varia nel tempo la temperatura nei suoi vari punti.
Medicina
La funzione dell’e., cioè la posizione e il controllo della posizione e del movimento del corpo nello spazio, si basa su una complessa rete di organi e vie nervose. L’organo periferico, il labirinto vestibolare, è situato nell’orecchio interno, e consiste in delicate formazioni (canali semicircolari, membrane otolitiche, endolinfa) capaci di registrare sulle terminazioni periferiche del nervo vestibolare mutamenti di e. statico e dinamico del capo nelle tre direzioni spaziali. Le fibre di questo nervo conducono gli stimoli ai nuclei del tronco encefalico e di là per nuove vie ai muscoli (per il tono di conservazione e di recupero del turbato e.) al cervelletto (organo centrale tonico e statico), ai nuclei oculomotori, e ad altre regioni del cervello. Con tali connessioni si spiegano i fenomeni provocati dalla stimolazione artificiale vestibolare (rotatoria, calorica, galvanica) e dalle lesioni dell’apparato descritto per cause molteplici: traumatiche, circolatorie, tossi-infettive, tumorali. I più importanti di questi fenomeni sono: il nistagmo, la deviazione degli indici e della marcia o la caduta in posizione eretta, la vertigine.
In senso traslato, il termine si adopera in fisiologia per indicare costanti organiche alla cui conservazione, essenziale per la vita, provvedono sistemi fisico-chimici che si oppongono a mutamenti patologici. I più importanti e. sono l’e. idro-elettrolitico, l’e. acido-base, l’e. endocrino. L’ e. idro-elettrolitico è regolato dal rene; condizioni patologiche che alterano la funzione renale o il bilancio idrico (vomito, diarrea) possono comprometterlo e causare anche la morte del paziente. Ugualmente importante è l’ e. acido-base in quanto la costanza della concentrazione idrogenionica (pH) è condizione essenziale per i processi vitali. L’ e. endocrino viene mantenuto fondamentalmente mediante la retroazione (feedback) di sostanze ormonali e non.
Meteorologia
E. atmosferico
Indica lo stato dinamico di masse d’aria soggette a moti verticali: si parla precisamente di e. stabile, instabile o indifferente a seconda che una massa d’aria spostata verticalmente tenda, rispettivamente, a ritornare nella posizione di partenza oppure prosegua indefinitamente nel suo moto oppure resti in quiete nella posizione d’arrivo. Lo stabilirsi dell’uno o dell’altro tipo di e. è in relazione con il gradiente termico verticale dell’atmosfera. Posto che i moti verticali dell’aria avvengono in pratica adiabaticamente, la variazione della temperatura della massa d’aria in moto è di circa −1 °C/100 m (per aria secca), che è il cosiddetto gradiente verticale adiabatico; si ha e. stabile oppure instabile oppure indifferente a seconda che il gradiente termico verticale effettivo sia minore, maggiore o uguale rispetto a quello adiabatico.
Politica
E. politico
Canone fondamentale di politica internazionale consistente nell’equilibrare le forze delle grandi potenze in modo che la bilancia politica non penda in favore di una di esse.
Un e. tra gli Stati venne realizzato con la pace di Lodi (1454); in seguito, la dottrina dell’e. fu ripresa dai diplomatici europei per opporsi al tentativo di monarchia universale della Spagna prima e della Francia poi e trovò la sua classica formulazione soprattutto in Inghilterra all’inizio del 18° sec., durante la guerra per la successione spagnola; fu poi uno dei cardini del Congresso di Vienna (1814-15). Il sistema degli Stati europei, fondato sull’e., caratterizzò l’ultimo lungo periodo di pace in Europa (1871-1914). Dopo la Seconda guerra mondiale si è parlato di e. politico con riferimento al rapporto di forze tra URSS e USA.

![[1]](https://images.treccani.it/ext-tool/intra/thumbs_medium/a/ab/FORMULE_equilibrio_01.jpg)
![[2]](https://images.treccani.it/ext-tool/intra/thumbs_medium/5/5a/FORMULE_equilibrio_02.jpg)
![[3]](https://images.treccani.it/ext-tool/intra/thumbs_medium/0/02/FORMULE_equilibrio_03.jpg)
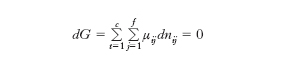
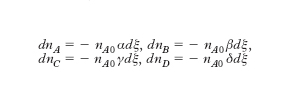
![[5]](https://images.treccani.it/ext-tool/intra/thumbs_medium/1/13/FORMULE_equilibrio_06.jpg)
![[6]](https://images.treccani.it/ext-tool/intra/thumbs_medium/f/f8/FORMULE_equilibrio_07.jpg)
![[7]](https://images.treccani.it/ext-tool/intra/thumbs_medium/2/23/FORMULE_equilibrio_08.jpg)
![[8]](https://images.treccani.it/ext-tool/intra/thumbs_medium/3/34/FORMULE_equilibrio_09.jpg)
![[9]](https://images.treccani.it/ext-tool/intra/thumbs_medium/3/37/FORMULE_equilibrio_10.jpg)