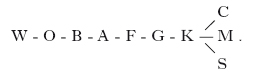stella
Astronomia
Secondo la definizione tradizionale, corpo celeste che brilla di luce propria, perché costituito di materia incandescente, a differenza di un pianeta che si limita a riflettere la luce ricevuta dal Sole o da un’altra stella. La distinzione fra s. e pianeti non è, però, così netta, in quanto i pianeti maggiori del Sistema solare (Giove e Saturno) irradiano nello spazio più energia di quanta ne ricevono dal Sole, comportandosi così come minuscole stelle. Con più precisione, per s. si intende un corpo che, in alcune fasi della vita, sviluppa nel suo interno reazioni di fusione nucleare. Tuttavia, il termine s. viene oggi impiegato estensivamente anche per indicare oggetti di massa relativamente piccola (detti nane brune) che, non riuscendo a innescare reazioni nucleari, irraggiano soltanto l’energia liberata nella contrazione gravitazionale.
Caratteristiche generali
Nomenclatura
Le s., anche se osservate con i più potenti telescopi, a causa della loro enorme distanza ci appaiono come puntiformi. A occhio nudo se ne riescono a distinguere non più di 6000 (quelle la cui magnitudine apparente è minore di 6). Le s. più luminose sono designate con nomi propri, come, per es., Arturo, Altair, Vega ecc.; alcune di queste s. sono, in realtà, doppie, sicché vengono distinte con le lettere A, B: per es., Sirio A e Sirio B, Procione A e Procione B ecc. Per localizzare le s. principali si usa una nomenclatura binomia, consistente in una lettera dell’alfabeto greco (α, β, γ ecc., assegnata generalmente in ordine di luminosità decrescente) seguita dal genitivo del nome latino della costellazione di appartenenza: così, le s. Betelgeuse, Rigel, Bellatrix e Mintaka, che si trovano nella regione della volta celeste occupata dalla costellazione di Orione, vengono indicate rispettivamente come α Orionis, β Orionis, γ Orionis e δ Orionis.
Spettro e temperatura superficiale
L’emissione elettromagnetica delle s. consiste, in generale, di uno spettro continuo, approssimativamente di corpo nero, al quale sono sovrapposte numerose righe (ed eventualmente bande) di assorbimento. Il colore di una s. dipende dalla sua temperatura superficiale. Dato che, alle lunghezze d’onda visibili, la s. si comporta con buona approssimazione come un corpo nero, il massimo dell’emissione cade alla lunghezza d’onda λm=0,29/T (dove λm è misurata in centimetri e la temperatura T in kelvin). Si trova, per es., che λm per 3000 K<T<4000 K cade nel rosso, nel giallo per 5000 K<T<6000 K, nel blu o nell’ultravioletto per temperature superiori. Quindi per individuare il colore di una s. si deve conoscere la sua λm; il Sole, per es. (T ≃ 5800 K), è una s. gialla. Individuare la lunghezza d’onda λm non è facile sperimentalmente; si preferisce, allora, caratterizzare il colore di una s. con il suo indice di colore. Questo viene determinato mediante tecniche fotometriche: fotometria a 3, a 4 o a 5 colori (➔ fotometria). La fotometria a 5 colori consiste nel misurare l’intensità della radiazione emessa dalla s. in 5 bande di lunghezza d’onda (ultravioletto, blu, giallo-verde, rosso, infrarosso), utilizzando appositi filtri. La differenza fra le magnitudini determinate in due diverse bande fornisce un indice di colore. Si definiscono così vari indici. Quelli più usati sono: B-V, U-V, V-R, dove U, B, V e R indicano, rispettivamente, le magnitudini della s. nell’ultravioletto, nel blu, nel visuale e nel rosso. La scala di magnitudini ai vari colori viene normalizzata in modo che tutti gli indici abbiano valore 0 per s. con una temperatura superficiale di 104 K (classe spettrale A0). Le s. più calde (T>104 K) presentano indici di colore negativi, quelle più fredde (T<104 K) indici positivi. Il Sole ha, per es., B-V=0,66. Dai valori di questi indici, assumendo che la forma dello spettro continuo di emissione sia quello caratteristico di un corpo nero, si deduce la temperatura superficiale della stella. Più propriamente, la temperatura così ottenuta viene chiamata temperatura di colore (Tc), per distinguerla da quella che viene chiamata temperatura efficace (Teff), definita come la temperatura di un corpo nero che emetta, per unità di superficie e di tempo, la stessa quantità di energia irradiata dalla stella. Lo spettro di righe, sovrapposto allo spettro continuo, dipende dall’assorbimento dei gas atmosferici più freddi ed è, quindi, analogo allo spettro di Fraunhofer del Sole (➔). Le sue caratteristiche, che variano a seconda della temperatura e della composizione chimica dell’astro, vengono utilizzate nella classificazione spettrale delle stelle.
Luminosità
La luminosità di una s. (L) è definita come la quantità di energia che questa irradia nell’unità di tempo. Essa viene misurata in watt, o, più comunemente, in unità di luminosità del Sole (L⊙=3,85∙1026 W). La luminosità di una s. è legata alla sua magnitudine bolometrica assoluta dalla relazione: Mbol=Mbol,⊙−2,5 log(L/L⊙), dove Mbol,⊙=4,74 è la magnitudine bolometrica assoluta del Sole. Mbol, e quindi L, vengono dedotte dalla magnitudine bolometrica apparente della s. (mbol), una volta che sia nota la sua distanza (➔ fotometria). La luminosità delle s. varia entro limiti assai ampi: da ∼10−5L⊙ a ∼106 L⊙.
Per le distanze delle s. ➔ distanza.
Classificazione delle stelle
La classificazione stellare più largamente usata adotta uno schema a 3 parametri. Essa distingue le s. in: tipi (o classi) spettrali (in base alle caratteristiche del loro spettro), classi di luminosità (in base alla loro luminosità) e popolazioni (in base alla composizione chimica).
Tipi spettrali
Il primo tentativo di classificazione spettrale delle s. fu compiuto, tra il 1863 e il 1868, da A. Secchi, che, con sole osservazioni visuali, studiò circa 500 s., dividendole in 4 categorie (bianco-azzurre, gialle, arancioni e rosse). La classificazione moderna fu sviluppata negli USA all’osservatorio di Harvard e prende perciò il nome di classificazione di Harvard. Nella sua versione attuale, tale classificazione raggruppa le s. in 10 tipi spettrali principali, ordinati secondo la sequenza:
Procedendo dal tipo W (s. di Wolf-Rayet) ai tipi C, M, S, la temperatura superficiale diminuisce da ∼105 K a ∼3∙103 K. I tipi M, C e S sono ‘paralleli’, nel senso che comprendono s. con temperature simili, ma composizioni chimiche diverse. Al diminuire della temperatura, come già detto, il massimo di intensità dello spettro continuo si sposta verso le lunghezze d’onda più lunghe, sicché il colore della s. cambia, passando dal violetto (W) fino al rosso (M, C, S). Ciascun tipo spettrale viene, a sua volta, suddiviso in 10 sottotipi, distinti con un indice da 0 a 9. Per es., il Sole è una s. gialla di tipo G2.
Si usa anche indicare come primitivi i tipi W, O, B, come avanzati quelli K, C, M, S e come intermedi gli altri (A, F, G). Le caratteristiche di ciascun tipo spettrale sono elencate nella tab. 1.
Classi di luminosità
La catalogazione delle s. in classi di luminosità venne introdotta, nel 1943, dagli astronomi statunitensi W.W. Morgan e P.C. Keenan, dell’osservatorio Yerkes, e prende perciò il nome di classificazione di Yerkes o classificazione MK. Nella sua versione più recente, essa raggruppa le s. in 6 classi, la prima delle quali comprende due sottoclassi: Classe Ia: Supergiganti più luminose; Classe Ib: Supergiganti meno luminose; Classe II: Giganti luminose; Classe III: Giganti normali; Classe IV: Subgiganti; Classe V: Nane; Classe VI: Subnane. Per es., il Sole è una s. nana, sicché, appartenendo al tipo spettrale G2, viene catalogato come G2-V. I nomi (supergiganti, giganti ecc.) con cui si indicano queste classi discendono dal fatto che la luminosità di una s. dipende soprattutto dalle sue dimensioni, sicché le s. più luminose sono, in generale, quelle più grandi. Le s. supergiganti e nane possono appartenere a quasi tutti i tipi spettrali; le giganti sono invece generalmente dei tipi spettrali intermedi o avanzati; le subnane soltanto dei tipi intermedi. Rimangono fuori da questo schema le s. meno luminose, che costituiscono la classe delle nane bianche, indicate con la lettera D seguita da quella corrispondente al tipo spettrale (per es., DA, DO, DM).
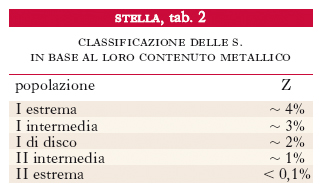
Popolazioni
Si usa descrivere molto schematicamente la composizione chimica di una s. con 3 parametri, X, Y e Z, che rappresentano rispettivamente le abbondanze percentuali (in massa) dell’idrogeno, dell’elio e di tutti gli altri elementi, conglobati sotto l’unica dizione di ‘metalli’. Negli anni 1940, W. Baade introdusse per primo la distinzione delle s. in 2 popolazioni (I e II) in base al loro contenuto metallico. Oggi si adotta una classificazione più dettagliata, descritta nella tab. 2, che raggruppa le s. in 5 categorie a seconda del valore di Z. Il contenuto metallico di una s. è un indice della sua età: le s. più antiche sono quelle di popolazione II estrema, formatesi dalla materia primordiale, nella quale gli elementi più pesanti dell’elio erano quasi assenti; le s. più giovani sono, invece, quelle di popolazione I estrema, che hanno tratto origine da materia arricchita di metalli dalle s. delle generazioni precedenti tramite i processi di nucleosintesi stellare (➔ elemento). Il Sole è una s. di popolazione I di disco. Alla popolazione I appartiene la maggioranza delle s. più vicine al Sole.
Diagramma di Hertzsprung-Russell
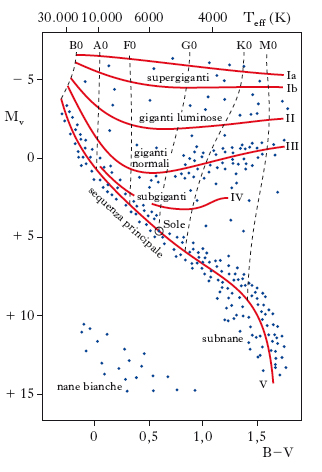
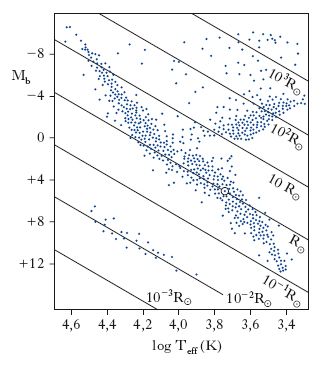
E. Hertzsprung e H.N. Russell studiarono la relazione fra le magnitudini assolute e i tipi spettrali delle s., elaborando (1913) un grafico che da loro prese il nome di diagramma di Hertz;sprung-Russell o, più brevemente, diagramma H-R. Esistono varie versioni di tale grafico. In quello di fig. 1, in ascissa sono riportate 3 scale, fra loro equivalenti: i tipi spettrali (da B0 a M0), l’indice di colore B-V e la temperatura efficace Teff (in scala logaritmica); in ordinata è riportata la magnitudine visuale assoluta (MV). Si nota che i punti rappresentativi delle s. non si distribuiscono uniformemente, ma si raggruppano in regioni ben determinate. La maggior parte delle s. si concentra lungo una striscia che attraversa diagonalmente il diagramma e che prende il nome di sequenza principale. Le s. che ne fanno parte sono quelle della V e VI classe di luminosità (s. nane e subnane). Le s. residue si addensano anch’esse in fasce, che corrispondono alle altre classi di luminosità (supergiganti, giganti luminose, giganti normali, subgiganti). In basso, a sinistra, si trova il raggruppamento delle nane bianche. Il Sole si colloca all’incirca al centro della sequenza principale. Spesso, nel diagramma H-R, in ordinata si riporta la magnitudine bolometrica assoluta, anziché quella visuale, o la luminosità, quest’ultima in scala logaritmica.
Parametri stellari fondamentali
Massa
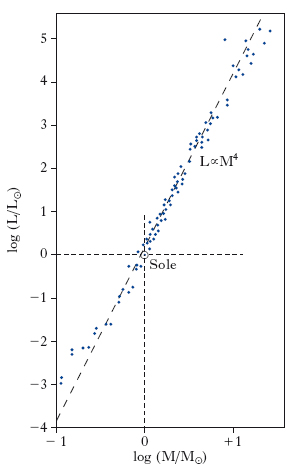
Misure dirette delle masse stellari sono possibili soltanto per le componenti di sistemi binari. Complessivamente, è stata determinata con buona accuratezza la massa di un centinaio di s., in gran maggioranza appartenenti alla sequenza principale. Per tali s. si è trovato che massa e luminosità sono legate dalla relazione illustrata in fig. 2. Sull’asse delle ascisse di questo grafico (che prende il nome di diagramma massa-luminosità) sono riportate le masse (M) delle s., su quello delle ordinate le loro luminosità (L), entrambe in scala logaritmica. I punti si distribuiscono approssimativamente intorno alla retta tratteggiata, che corrisponde a una legge del tipo: L∝M4. Si notano, tuttavia, scostamenti significativi da questo andamento medio per le s. di massa maggiore di ∼10 M⊙ e per quelle di massa minore di ∼0,4 M⊙.
Dal punto di vista teorico, ci si aspetta che le s. più massicce siano anche più luminose: infatti, quanto maggiore è la massa di una s., tanto più elevata è la sua temperatura interna e, quindi, più rapido il ritmo con cui si sviluppano le reazioni nucleari che riforniscono l’astro di energia. Più precisamente, la teoria della struttura stellare fa prevedere che la massa e la luminosità delle s. di sequenza principale siano legate da una relazione del tipo L∝Ma, con a=3-4, in buon accordo con i dati sperimentali. La relazione massa-luminosità ha una grande importanza pratica perché permette di stimare la massa di s. per le quali non è possibile una misura diretta di questa grandezza, ma di cui è nota la luminosità. Si è trovato così che le s. raggiungono, al massimo, masse di 50-100 M⊙, dove M⊙=1,989∙1030 kg è la massa del Sole (∼40 M⊙ è il valore più grande di una massa stellare ottenuto con una misura diretta). Questi risultati sono coerenti con le aspettative teoriche: si calcola, infatti, che una s. con M>100 M⊙ si disintegrerebbe perché la pressione di radiazione prevarrebbe sulla forza attrattiva gravitazionale.
Per quanto riguarda le s. meno massicce, la teoria della struttura stellare indica che le reazioni di fusione nucleare possono svilupparsi soltanto in corpi che abbiano una massa maggiore di 0,08 M⊙; gli oggetti di massa più piccola vanno sotto il nome di nane brune. Sono state individuate numerose s. con massa intorno a 0,2 M⊙, ma relativamente poche con masse più piccole. Al di là delle difficoltà legate alla rivelazione di questi corpi che hanno una luminosità assai debole (per una s. di 0,2 M⊙, L∼10−3 L⊙), sembra accertato che essi siano relativamente rari.
Poche misure di massa sono state ottenute per s. non appartenenti alla sequenza principale; per le nane bianche, in particolare, non esiste una relazione che leghi la luminosità alla massa, in quanto l’energia che esse irradiano diminuisce gradualmente con l’età dell’astro.
Dimensioni
Nella grande maggioranza dei casi i raggi delle s. vengono ricavati dalla legge di Stefan: L=4πR2σTeff4, una volta che siano noti i valori della luminosità L e della temperatura efficace Teff. In pratica, si può utilizzare il diagramma H-R di fig. 3, in cui le rette inclinate rappresentano la relazione fra magnitudine bolometrica assoluta e temperatura efficace, per s. di vario raggio. Le s. più piccole, che appaiono nel diagramma, sono le nane bianche, che hanno raggi dell’ordine di 0,01 R⊙ (dove R⊙=6,96∙108 m è il raggio del Sole); le più grandi sono le supergiganti, che hanno raggi di 1000 R⊙ e oltre. Bisogna ricordare, tuttavia, che nell’Universo esistono s. di dimensioni ancora più piccole delle nane bianche: le s. di neutroni e i buchi neri.
Rotazione
Il metodo di misura più diretto delle velocità di rotazione delle s. si basa sull’effetto Doppler. Supponendo, per semplicità, che l’asse di rotazione della s. sia perpendicolare alla linea di vista, si trova che, a ogni istante, metà del disco stellare si muove verso l’osservatore, mentre l’altra metà se ne allontana. Le righe dello spettro, di conseguenza, sono spostate verso le lunghezze d’onda più corte sulla prima metà del disco e verso le lunghezze d’onda più lunghe sulla seconda. Si è così riusciti a stimare la velocità di rotazione di alcune migliaia di s., appartenenti a numerosi tipi spettrali e classi di luminosità. Per le s. di sequenza principale, i periodi di rotazione variano da circa 50 giorni a meno di 1 giorno. Le massime velocità di rotazione equatoriali osservate sono di ∼500 km/s, vicine al valore limite oltre il quale la forza centrifuga disgregherebbe l’astro. Le s. in rotazione più veloce sono quelle di massa maggiore: infatti, le s. con M>1,5 M⊙ hanno, in media, una velocità equatoriale di ∼200 km/s, mentre quelle con M<M⊙ raramente superano la velocità di 5 km/s. Il Sole, la cui velocità equatoriale è ∼2 km/s, si colloca fra le s. in rotazione più lenta. Finora non è stato possibile stabilire se altre s. hanno, come il Sole, una rotazione differenziale in latitudine.
Per quanto riguarda le s. non appartenenti alla sequenza principale, le subgiganti e le giganti ruotano, in generale, piuttosto lentamente; le nane bianche, invece, hanno periodi assai brevi, fra ∼100 minuti e ∼3 giorni, anche se, a causa delle loro piccole dimensioni, le velocità equatoriali non sono molto elevate (∼20 km/s). Periodi di rotazione di gran lunga più brevi (da ∼2 ms a ∼4 s) hanno le pulsar.
Struttura ed evoluzione stellare
Sorgenti di energia
Le s. si formano a seguito del collasso gravitazionale di nubi di gas e polvere. Pertanto, nelle prime fasi della loro vita, esse sono riscaldate dalla energia gravitazionale, liberata nella contrazione, che si trasforma in energia termica. Se la massa stellare supera un valore critico (∼0,08 M⊙), a un certo punto la temperatura interna diventa abbastanza elevata da innescare reazioni di fusione nucleare. Queste reazioni, fortemente esotermiche, rappresentano la principale fonte di energia che alimenta le stelle. I processi di fusione nucleare sono diversi a seconda della temperatura interna e della composizione chimica della stella. Tali caratteristiche, a loro volta, dipendono sia dalla massa dell’astro sia dalla fase della storia evolutiva che esso sta attraversando.
Le prime reazioni nucleari che si sviluppano sono quelle che conducono alla fusione dell’idrogeno in elio. Ciò sia perché l’idrogeno è l’elemento più abbondante nelle s., sia perché la temperatura di soglia per tale processo è relativamente bassa (∼4∙106 K). Vi sono due meccanismi con cui può avvenire la fusione dell’idrogeno: il ciclo protone-protone (o ciclo p-p) e il ciclo CNO (o ciclo del carbonio o ciclo di Bethe; ➔ Sole). Il ciclo p-p prevale se la temperatura centrale è inferiore a ∼ 2∙107 K (il che si verifica nelle s. con M≲1,5 M⊙); il ciclo CNO diventa invece dominante se la temperatura supera tale valore (s. con M≳1,5 M⊙). Il risultato finale di entrambi i cicli è la fusione di 4 protoni in un nucleo di elio, con la liberazione di un’energia di 26,7 MeV.
Quando una s. ha ‘bruciato’ l’idrogeno disponibile, se la sua massa è abbastanza grande (M≳0,5 M⊙) si innesca la fusione dell’elio in carbonio attraverso le reazioni: 4He+4He→8Be; 8Be+4He→12C+γ, dove γ è un fotone. Le due reazioni devono avvenire quasi simultaneamente, perché il 8Be è instabile e in 2∙10−16 s decade generando nuovamente 2 nuclei di elio. Questo processo (noto come ciclo 3α perché a esso partecipano 3 nuclei di elio o particelle α) ha una temperatura di soglia di ∼108 K e conduce alla liberazione di un’energia di 7,27 MeV. Alle reazioni precedenti si accompagna la cattura di particelle α da parte di nuclei di carbonio con formazione di ossigeno: 12C+4He→16O+γ. Alcuni nuclei di ossigeno possono, a loro volta, catturare particelle α trasformandosi in neon e, poi, in magnesio.
Quando si è esaurito l’elio disponibile, nelle s. più massicce (M≳8 M⊙) si sviluppano ulteriori reazioni nucleari, che conducono alla produzione di silicio (28Si) e di ferro (56Fe). Con la formazione di 56Fe, il nucleo più stabile che esista in natura, ha termine la sequenza dei processi di fusione che avvengono nelle s., perché la generazione di elementi ancora più pesanti avverrebbe attraverso reazioni endotermiche, cioè con assorbimento di energia.
Meccanismi di trasporto dell’energia
L’energia, prodotta nel nucleo di una s., viene trasportata in superficie soprattutto con due meccanismi: l’irraggiamento (trasporto radiativo) e la convezione (trasporto convettivo). Il trasporto radiativo si realizza, senza movimento di materia, attraverso l’assorbimento e la riemissione di fotoni da uno strato della s. al successivo; il trasporto convettivo, invece, attraverso correnti che rimescolano il materiale stellare: si usa pertanto parlare nel primo caso di equilibrio radiativo, nel secondo di instabilità convettiva.
Formazione delle stelle
Le s. traggono origine dal collasso gravitazionale di nubi molecolari, immensi aggregati di gas e polvere relativamente densi (ρ∼2∙10−21 g∙cm−3) e freddi (T∼10 K; ➔ gas). Affinché la forza attrattiva di gravità prevalga sulla pressione del gas, determinandone la contrazione, occorre che la massa della nube superi un valore critico, noto come massa di Jeans (MJ). MJ è tanto più piccola quanto più fredda o densa è la nube; più precisamente si trova: MJ=[(2,5 kT)/(Gμ)]3/2∙[3/(4πρ)]1/2, dove k è la costante di Boltzmann, T la temperatura, G la costante di gravitazione universale, μ la massa media di una particella e ρ la densità della nube. Per ρ=2∙10−21 g∙cm−3 e T∼10 K, si ha: MJ=8 M⊙. Poiché le nubi molecolari raggiungono masse di gran lunga maggiori (104-106 M⊙), le condizioni per il collasso sono soddisfatte. Questo si sviluppa nella zona centrale della nube, dove la densità raggiunge i valori più elevati (ρ∼10−19 g∙cm−3). Una volta iniziata la contrazione, la densità aumenta e, quindi, il valore della massa di Jeans diminuisce: di conseguenza, la nube può spezzarsi in frammenti, ciascuno dei quali collassa separatamente, dando origine a una stella. Il collasso gravitazionale è un processo assai rapido, che si svolge sul tempo di scala dinamico, τd∼104 anni. L’oggetto che si forma prende il nome di protostella.
Fase di pre-sequenza
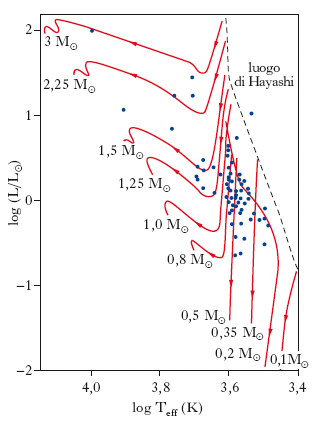
Quando il collasso gravitazionale ha termine e la s. raggiunge una configurazione di equilibrio idrostatico, il suo punto rappresentativo nel diagramma H-R cade in quello che viene detto luogo di Hayashi (fig. 4). In seguito, la s. continua a contrarsi, anche se più lentamente, sicché la sua temperatura interna aumenta. Nel diagramma H-R, essa percorre, a seconda della sua massa, una delle tracce evolutive illustrate in fig. 4, fino a raggiungere la sequenza principale. Il suo punto rappresentativo si sposta prima verso il basso (perché il suo raggio e, quindi, la luminosità diminuiscono) e poi verso sinistra e un po’ verso l’alto (perché la sua temperatura cresce così fortemente da determinare un aumento di luminosità nonostante il proseguire della contrazione). La durata di questo periodo della vita della s., che prende il nome di fase di pre-sequenza, può andare da meno di 105 anni per le s. più massicce (M>10 M⊙) a oltre 108 anni per quelle di massa più piccola. Mentre la s. attraversa la fase di pre-;sequenza, la sua struttura cambia. Inizialmente, quando si trova nel luogo di Hayashi, essa è interamente convettiva perché, essendo ancora abbastanza fredda, la sua opacità è elevata; in seguito, con il crescere della temperatura, l’opacità degli strati interni diminuisce, sicché la s. sviluppa un nucleo radiativo, mantenendo soltanto un mantello convettivo (ciò, tuttavia, non accade nelle s. di massa inferiore a ∼0,25 M⊙, che rimangono interamente convettive).
Fase di sequenza principale
Alcune reazioni nucleari, che coinvolgono il deuterio e il litio, si sviluppano nelle s. già in fase di pre-sequenza. L’ingresso nella fase di sequenza principale è segnato, però, dalla ‘accensione’ dell’idrogeno, che si verifica quando la temperatura interna raggiunge ∼4∙106 K. Non entrano nella sequenza principale le nane brune di massa inferiore a ∼0,08 M⊙, la cui temperatura interna rimane sempre al di sotto di tale soglia. Nel diagramma H-R, la traccia evolutiva di tali s. scende dapprima verticalmente verso il basso (perché la luminosità decresce a causa della progressiva diminuzione del raggio, mentre la temperatura superficiale rimane quasi costante) e poi, continuando ad andare verso il basso, devia verso destra (perché la contrazione cessa e la s. si raffredda man mano che irradia l’energia termica di cui dispone).
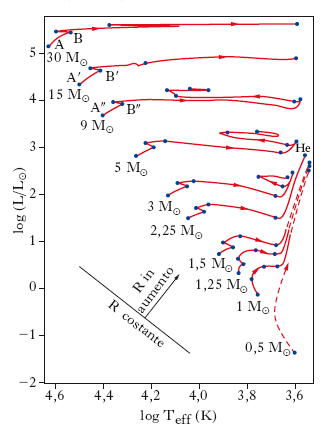
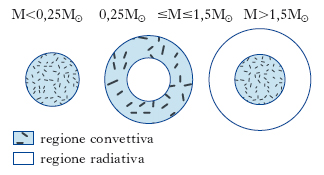
Per le s. che la attraversano, la fase di sequenza principale, definita come il periodo in cui nel nucleo avviene la fusione dell’idrogeno, è la più lunga della vita: essa, infatti, si svolge sulla scala di tempo τnH, che varia, a seconda della massa, da ∼2∙106 anni, per M=30 M⊙, a ∼1010 anni, per M=0,25 M⊙. Durante tutto questo periodo la luminosità e la temperatura della s. subiscono soltanto un leggero aumento, sicché il suo punto rappresentativo nel diagramma H-R si sposta di poco (tratti AB, A′B′, A″B″, ... delle tracce evolutive in fig. 5). Ciò spiega perché nel diagramma i punti si addensino intorno alla diagonale. D’altra parte, poiché τnH aumenta al diminuire della massa, la maggiore concentrazione di punti si verifica nella parte bassa della sequenza principale dove cadono le s. meno massicce. Le modalità con cui avviene la fusione dell’idrogeno dipendono dalla massa della stella. Se M<1,5 M⊙, la temperatura centrale rimane inferiore a 2∙107 K, sicché prevale il ciclo p-p; se M>1,5 M⊙, la temperatura supera tale soglia e diventa dominante il ciclo CNO. Ciò ha importanti conseguenze sulla struttura della s. (fig. 6). Infatti, nel primo caso essa conserva la struttura che aveva nella fase di pre-sequenza, cioè è interamente convettiva se M<0,25 M⊙, mentre è costituita da una regione interna radiativa e da un mantello convettivo se ha una massa maggiore. Nel secondo caso, invece, essa sviluppa un nucleo convettivo, perché le reazioni del ciclo CNO sono confinate a una zona centrale molto ristretta, determinando ivi un gradiente di temperatura assai elevato, mentre il mantello, dove la temperatura diminuisce più gradualmente, diventa radiativo.
Fase di gigante
Quando una s. lascia la sequenza principale (punti B, B′, B″, ... in fig. 5), la combustione dell’idrogeno, esauritasi nel nucleo, prosegue in strati via via più esterni. Il nucleo, formato prevalentemente da elio, continua ad accrescersi e, non essendo più sostenuto dall’energia sviluppata nelle reazioni nucleari, si contrae per effetto della gravità. Gli strati esterni, invece, si espandono e la s. diventa una gigante. Le tracce evolutive piegano verso destra e poi, almeno per masse non troppo grandi, verso l’alto (fig. 5), perché il raggio e, quindi, la luminosità aumentano mentre la temperatura superficiale diminuisce, ma presentano varie peculiarità (oscillazioni verso destra e verso sinistra, cappi). I processi che avvengono in questo periodo della vita di una s., detto fase di gigante, sono complessi e non possono essere descritti qui in dettaglio. Nelle s. con M>0,5 M⊙, il cui nucleo raggiunge temperature superiori a 108 K, si innesca la fusione dell’elio. Le reazioni del ciclo 3α si instaurano gradualmente nelle s. più massicce (M>1,5 M⊙), mentre in quelle di massa minore (0,5 M⊙<M<1,5 M⊙), iniziano in modo brusco, dando luogo a una improvvisa espansione del nucleo, detta flash dell’elio, che, tuttavia, non conduce alla disintegrazione della stella. Quando l’elio si è esaurito nel nucleo, la sua combustione può continuare nel guscio circostante. Nelle s. con M≲3 M⊙, il carbonio e l’ossigeno, originati dalla fusione dell’elio, non danno luogo ad altre reazioni nucleari: alla fine della fase di gigante, la pressione di radiazione espelle gli strati esterni, che formano una nebulosa planetaria, e la s. diventa una nana bianca.
Notevoli incertezze esistono sull’evoluzione delle s. con massa fra 3 M⊙ e 8 M⊙. È possibile che nel nucleo di queste s. si inneschi in modo improvviso la fusione del carbonio e dell’ossigeno (flash del carbonio e dell’ossigeno), provocando una esplosione di supernova. Sembra però più probabile che, prima che ciò accada, la s. riduca la sua massa, espellendo gli strati più esterni (che andrebbero a formare una nebulosa planetaria): in questo caso, nel nucleo non si svilupperebbero altre reazioni nucleari e l’astro evolverebbe verso lo stadio di nana bianca, come le s. di massa più piccola. Nelle s. di massa ancora maggiore (M>9 M⊙) la combustione del carbonio e dell’ossigeno si instaura gradualmente e i processi di fusione nucleare continuano fino alla formazione del silicio e del ferro.
La configurazione che la s. raggiunge non è stabile: quando si spengono le reazioni nucleari che sostenevano l’astro, questo collassa dando luogo a una esplosione di supernova. Il nucleo centrale della s., che sopravvive alla deflagrazione, si trasforma, a seconda della sua massa residua, in una s. di neutroni o in un buco nero.
Le ultime fasi della vita di una stella
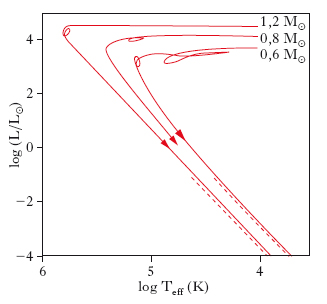
La fig. 7 mostra le tracce evolutive, nel diagramma H-R, di s. di varie masse, in uscita dalla fase di gigante. Le masse considerate nel grafico (da 0,6 M⊙ a 1,2 M⊙) sono quelle del nucleo residuo della s., dopo l’espulsione degli strati esterni: pertanto, quanto detto si applica a tutte le s., la cui massa originaria era inferiore a 3-8 M⊙. Si nota che, in un primo momento, il punto rappresentativo della s. si sposta quasi orizzontalmente da destra verso sinistra, perché l’astro si contrae e la sua temperatura superficiale aumenta, di modo che la luminosità si mantiene quasi costante. Dopo avere raggiunto una temperatura massima di 105-106 K, stadio di nana blu, la s. cessa di contrarsi e si raffredda man mano che irradia l’energia termica posseduta. La traccia piega allora verso il basso e verso destra, lungo una linea di raggio costante (cfr. fig. 3).
Questo periodo conclusivo della vita di una s. (fase di nana bianca) si svolge sul tempo scala di raffreddamento, che è molto lungo. Per es., una s. con M=0,1 M⊙ impiega ∼ 2∙109 anni per portarsi alla temperatura Teff=1000 K, alla quale la sua luminosità si riduce a 10−5 L⊙ (valore al di sotto del quale la s., che prende il nome di nana nera, diventa praticamente inosservabile). Le nane bianche differiscono dalle nane brune per la composizione chimica. Queste ultime, infatti, non essendo mai state sede di reazioni nucleari, conservano la loro composizione originaria e, quindi, consistono soprattutto di idrogeno. Le nane bianche, invece, sono costituite prevalentemente di elio (nane bianche di elio) o di carbonio e ossigeno (nane bianche di carbonio e ossigeno), a seconda che provengano da una s. progenitrice di massa inferiore o superiore a ∼0,5 M⊙. Nelle nane bianche la materia si trova in uno stato di enorme compressione: infatti, dato che il raggio e la massa di questi corpi sono rispettivamente dell’ordine di 10−2 R⊙ e di 1 M⊙, la loro densità media è ∼106 g/cm3. In tali condizioni, nell’interno della s. gli elettroni costituiscono un gas di fermioni degenere (➔ statistica): l’astro non collassa per effetto della gravità, perché è sostenuto dalla pressione esercitata dal gas di elettroni degenere. D’altra parte, poiché la pressione di un tale gas degenere dipende solo dalla densità tramite la relazione P∝ρ5/3, al crescere della massa il raggio della s. deve diminuire affinché si raggiunga l’equilibrio fra forza di pressione e forza di gravità.
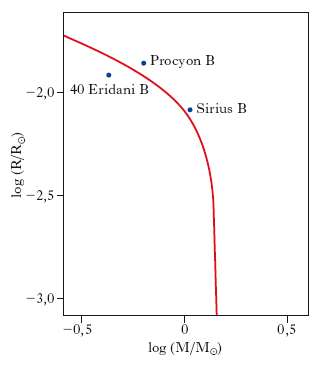
In fig. 8 la relazione massa-raggio, ottenuta teoricamente, è confrontata con i dati osservativi di 3 nane bianche: l’accordo, come si vede, è soddisfacente. Il grafico mostra anche che il raggio tende a zero per un valore critico della massa, che prende il nome di massa di Chandrasekhar (MCH). Questo fenomeno, che pone un limite superiore alla massa di una nana bianca, dipende dal fatto che, per densità dell’ordine di 1010 g/cm3, i nuclei degli atomi cominciano a catturare gli elettroni, sicché la pressione elettronica diminuisce e la s. collassa. Il valore di MCH dipende dalla composizione chimica della s., ma è comunque nell’intervallo 1,2-1,4 M⊙. Oggetti di massa maggiore di MCH hanno origine dai residui delle esplosioni di supernova delle s. con M≳9 M⊙. Se la massa del residuo non supera un altro valore critico (1,5-2,5 M⊙), noto come massa di Oppenheimer-Volkov (MOV), il collasso gravitazionale viene a un certo punto bloccato dalla pressione sviluppata dai neutroni, formatisi nel processo di cattura nucleare degli elettroni. L’equilibrio si raggiunge quando il raggio della s. si è ridotto a ∼10 km e, di conseguenza, la sua densità è ∼1014 g/cm3. Il corpo, che risulta allora costituito da un gas di neutroni degenere, prende il nome di s. di neutroni. Le s. di neutroni vengono identificate con le pulsar. Se, infine, il residuo dell’esplosione di supernova ha una massa maggiore di MOV, la pressione del gas di neutroni degenere non riesce mai a bilanciare la forza gravitazionale, sicché il collasso continua indefinitamente, dando origine a un buco nero. Si pensa che la formazione di una s. di neutroni o di un buco nero dipenda dalla massa della s. progenitrice (M≲30 M⊙ nel primo caso, M≳30 M⊙ nel secondo).
Moti delle stelle
Alcune s. (s. fisse) sembrano conservare sempre la stessa posizione nella sfera celeste; in realtà esse sono animate da moti propri, che però, a causa della grandissima distanza, non sono percettibili all’osservazione ordinaria. L’esistenza dei moti stellari è nota dal 1718, quando E. Halley scoprì che alcune s. occupavano nelle costellazioni posizioni un po’ diverse da quelle date nel catalogo compilato da Ipparco quasi 2000 anni prima e si rese conto che gli spostamenti non erano spiegabili considerando soltanto la precessione dell’asse di rotazione terrestre. La velocità di una s. in un sistema di riferimento eliocentrico (detta velocità spaziale, v) viene espressa come somma di due componenti: quella lungo la linea di vista (velocità radiale, vR) e quella in direzione perpendicolare a tale linea (velocità trasversa, vT), con v=√‾‾‾‾‾‾vR2+‾‾‾vT2‾‾‾‾‾.
La velocità radiale si ricava dallo spostamento Doppler delle righe dello spettro di assorbimento della stella. Si ha infatti: vR=c(ν-ν′)/ν, dove ν è la frequenza della riga in situazione di quiete, ν′ la frequenza osservata e c la velocità della luce nel vuoto; se la s. si allontana dall’osservatore, ν′<ν (spostamento verso il rosso) e quindi vR>0; se, invece, la s. si avvicina ν′>ν (spostamento verso il violetto) e quindi vR<0. Occorre poi correggere le misure, tenendo conto dei moti della Terra. I valori di vR che così si ottengono sono dell’ordine delle decine di km/s.
La velocità trasversa si ricava, invece, dal moto angolare apparente (detto moto proprio, μ) della s. sulla volta celeste e dalla sua distanza (d), con la formula: vT=4,74dμ, dove d è espresso in parsec, μ in secondi di arco all’anno e vT in km/s (4,74 è un fattore di conversione introdotto appunto per avere vT in km/s). I moti propri si ottengono con osservazioni fotografiche, ripetute a intervalli di un anno, riferendo le posizioni delle s. a un sistema di galassie lontane. Si tratta, in generale, di valori assai piccoli: poche centinaia di s. hanno un moto proprio maggiore di 1″/anno e soltanto una, la s. freccia di Barnard, della costellazione di Ofiuco, presenta l’eccezionale moto proprio di 10,3″ all’anno, il maggiore finora conosciuto (scoperto nel 1903 da E.E. Barnard all’osservatorio Yerkes).
Stelle doppie e sistemi multipli
Si ritiene che la maggior parte, forse i 2/3, delle s. non siano isolate, come il Sole, ma facciano parte di sistemi formati da 2 o più componenti, che orbitano intorno al comune centro di massa. Se le componenti sono soltanto due, si parla di s. doppie o di sistemi binari; se sono tre o più, di sistemi multipli. Alcune s. doppie si riconoscono anche a occhio nudo e sono, infatti, note fin dall’antichità. L’esempio più famoso è la coppia formata da Mizar (ζ Ursae maioris) e Alcor (80 Ursae maioris), che, in realtà, è un sistema triplo perché si è scoperto che Mizar è, a sua volta, una s. doppia. Le osservazioni a occhio nudo non permettono di distinguere le vere s. doppie da quelle chiamate doppie ottiche, che sono s., lontane fra loro, che ci appaiono vicine sulla volta celeste perché si trovano quasi sulla stessa linea di vista. La prima prova sicura dell’esistenza delle s. doppie fu ottenuta nel 1803 da F.W. Herschel, che riuscì a rivelare il moto orbitale delle due componenti il sistema di Castore (α Geminorum). Circa 30 anni dopo, F. Savary determinò i parametri orbitali della coppia ξ Ursae maioris, aprendo così la strada alle misure delle masse stellari (➔ massa). Oggi si conoscono moltissime s. doppie, appartenenti a tutti i tipi spettrali e, praticamente, in ogni fase della loro evoluzione. Solo per poche migliaia di esse si hanno, però, informazioni dettagliate sulle orbite.
Le dimensioni dei sistemi variano entro larghi limiti: le componenti possono, infatti, essere così vicine da possedere un inviluppo comune o trovarsi a distanze assai grandi, fino a 0,1 pc (∼20.000 UA). Corrispondentemente, i periodi di rivoluzione vanno da alcune ore, nei sistemi più ‘stretti’, a circa 1 milione di anni, in quelli più ‘larghi’. Le indagini statistiche indicano come valore mediano del periodo ∼10 anni e, quindi, separazioni comparabili con i raggi delle orbite dei pianeti del Sistema solare. Le orbite delle componenti sono ellittiche nei sistemi con periodi maggiori di ∼10 giorni e circolari in quelli con periodi più brevi; il fenomeno viene attribuito agli effetti delle interazioni mareali fra corpi vicini.
Lo studio dei sistemi binari ha un grande interesse non soltanto perché offre l’opportunità di misurare in modo diretto alcuni parametri stellari fondamentali (massa e raggio), ma anche perché l’evoluzione di una s. può essere fortemente condizionata dalla presenza di una compagna: per es., le esplosioni di nova e quelle di supernova del tipo I si verificano soltanto in s. doppie.
Botanica
Stella alpina
Erba perenne (Leontopodium alpinum (fig. 9), chiamata in ted. Edelweiss, delle Asteracee. Forma piccoli cespuglietti, biancastri per il denso tomento che riveste tutti gli organi, alti 3-20 cm; l’infiorescenza è un corimbo contratto di capolini, con il capolino centrale sessile, gli altri brevemente peduncolati, circondata da 7-8 grandi brattee disposte a stella. Cresce sulle Alpi, Pirenei, monti dell’Asia, nei pascoli e in luoghi sassosi, su substrati calcarei, generalmente al di sopra dei 1300 m. Nell’Appennino centrale è rappresentata da un tipo nano, Leontopodium nivale, con forme affini nella penisola Balcanica.
Stella di Natale
Arbusto (Euforbia pulcherrima) della famiglia delle Euforbiacee originaria dell’America Centrale, coltivata per le vistose brattee rosse che circondano l’infiorescenza. Fiorisce d’inverno e si usa per decorare gli ambienti nelle feste natalizie.
Fisica
Nella fisica nucleare, configurazione di tracce di particelle ionizzanti, osservabile in un rivelatore visualizzante, costituita da un insieme di tracce aventi origine in un punto.
Matematica
Nella geometria proiettiva, una delle forme fondamentali di 2ª specie (➔ forma); precisamente s. di rette (o di raggi) o s. di piani sono rispettivamente l’insieme di tutte le rette o dei piani dello spazio ordinario i quali passano per un punto detto centro della s.: gli elementi di una di tali s. sono ∞2. Se la s. si considera in uno spazio affine o euclideo, si distingue la s. propria dalla s. impropria a seconda che il centro sia al finito o all’infinito; nel secondo caso si ha quindi una s. di rette parallele a una direzione prefissata ovvero una s. di piani paralleli a una direzione prefissata.
Scienza militare
Nelle uniformi militari, sul bavero delle giacche o dei cappotti e sulla punta dei colletti, distintivo peculiare (più spesso chiamato stelletta) di appartenenza alle forze armate e ai corpi armati dello Stato.
Le s. a cinque punte come simbolo di appartenenza alle forze armate dello Stato italiano furono adottate per la prima volta nel 1871, con r.d. 571/13 dicembre 1871, per tutte le persone soggette alla giurisdizione militare come elemento di distinzione dai funzionari civili dello Stato. Come insegna di grado, posta, in numero variabile da 1 a 4, sulle spalline delle uniformi dell’Esercito, contraddistingue gli ufficiali inferiori (1 s. il sottotenente, 2 s. il tenente e 3 il capitano), gli ufficiali superiori quando accompagnata dalla corona turrita (1 s. il maggiore, 2 il tenente colonnello e 3 il colonnello), gli ufficiali generali quando accompagnata dalla greca (1 s. il generale di brigata, 2 il generale di divisione, 3 il generale di corpo d’armata; una quarta s., funzionale, è portata dal capo di Stato Maggiore o da altra alta carica speciale).
Zoologia
Stella marina
Nome comune degli Echinodermi Asteroidei (➔). S. serpentine Nome comune degli Echinodermi Ofiuroidi (➔).