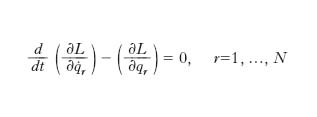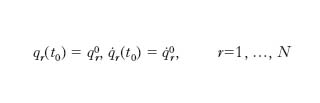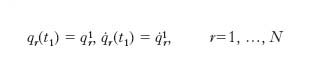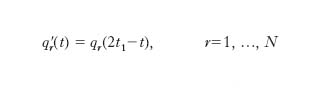tempo

Intuizione e rappresentazione della modalità con cui i singoli eventi si susseguono e sono in rapporto l’uno con l’altro (per cui essi avvengono prima, dopo o durante altri eventi), vista o come fattore che trascina l’evoluzione delle cose (lo scorrere del t.) o come scansione ciclica e periodica, a seconda che si enfatizzino l’irreversibilità delle vicende umane o il ricorrere degli eventi astronomici; tale intuizione è condizionata da fattori ambientali (i cicli biologici, il succedersi del giorno e della notte, il ciclo delle stagioni ecc.) e psicologici (gli stati della coscienza e della percezione, la memoria) e diversificata storicamente da cultura a cultura

Successione di eventi costituiti dal verificarsi di un dato fenomeno che si ripete uguale a se stesso (il passaggio della lancetta dell’orologio per una data posizione del quadrante, il raggiungimento del valore massimo da parte dell’intensità del campo elettrico di una radiazione monocromatica ecc.), che si può suddividere, misurare e distinguere in ogni sua frazione; per es. si ha la divisione del t. (in giorni, ore, minuti primi e secondi ecc.), secondo il moto apparente del Sole, la partizione del t. mediante il calendario, la misura del t. con l’orologio.

Arte

La rappresentazione iconografica del t. è elaborata sia come personificazione sia nel suo aspetto concettuale, attraverso simboli, episodi, allegorie che fanno riferimento al trascorrere del t. e ai suoi effetti. L’iconografia del t. come personificazione deriva dalla sovrapposizione medievale di due divinità: Chronos, dio greco del t., e Crono, padre di Zeus, che divorava i suoi figli nel timore di essere un giorno detronizzato da loro, la cui figura corrisponde nella mitologia romana a quella di Saturno. È dunque rappresentato comunemente come vecchio, barbuto, in identificazione o in analogia con la figura di Saturno; suoi attributi possono essere il serpente che si morde la coda o uroboro (ouroboros), la falce (originariamente riferita alla falciatura delle messi, presieduta da Saturno), simbolo dell’inesorabilità del suo trascorrere e comune anche alla rappresentazione della Morte; può essere alato. Frequente la rappresentazione della Verità svelata dal T., che ne scopre la nudità. L’avvio del t., inteso come circolarità e simboleggiato dall’anello dello Zodiaco, è concetto rappresentato in ambito cristiano dalla figura di Cristo Cronocratore, che presiede all’ordine del t., ruolo riservato nella mitologia alle divinità solari (Elio, Apollo). La stessa rappresentazione dello Zodiaco è frequente rappresentazione del t. fisico e soprattutto astrologico.

Collegata allo stesso concetto di successione e circolarità del t. è la rappresentazione dei mesi e delle stagioni, derivata dal mondo greco e romano, legata alla tipologia dei calendari ed espressa mediante personificazioni o allegorie, accompagnate da attributi astronomico-zodiacali, religiosi o agricoli. Dal 3° sec. in Occidente prevalgono raffigurazioni dei mesi attraverso scene di genere di soggetto rurale (arco di trionfo di Reims; mosaico da Saint Romain-en-Gal nel museo di Saint Germain-en-Laye). Nel Medioevo i mesi, a volte uniti ai segni zodiacali (archivolto del portale di Saint Lazare di Autun, Sainte Madeleine di Vézelay), appaiono in monumenti civili e religiosi (sculture di molti portali di chiese romaniche e gotiche: Notre-Dame di Parigi; Ferrara; S. Marco di Venezia ecc.; sculture di B. Antelami e scolari nel battistero di Parma), nelle miniature e illustrazioni di calendari, nella pittura murale (torre dell’Aquila nel castello del Buonconsiglio a Trento, inizio 15° sec.). Si sviluppa, accanto a quella dei mesi, la raffigurazione delle stagioni, anche queste rappresentate come personificazioni o divinità, in relazione alle stagioni agricole o come scene di genere riferite alle attività stagionali dell’uomo (Autunno come Bacco, in riferimento alla vendemmia; Inverno come Saturno, o come vecchio infreddolito; Primavera come Flora, in riferimento alla fioritura; Estate come Cerere, con simboli del raccolto dei frutti e delle messi). Sempre in riferimento al trascorrere del t. si hanno le raffigurazioni delle parti del giorno (Aurora, Crepuscolo, Notte, Giorno; le Ore).

Relative a risvolti filosofici, teologici, etici e morali del concetto di t., le raffigurazioni rivolte alle rappresentazioni delle età dell’uomo (le tre età), le rappresentazioni allegoriche della vita e della morte, le varie interpretazioni del concetto di vanitas, accanto alle raffigurazioni delle età del mondo: dalle quattro grandi ere della tradizione classica, in relazione alle stagioni naturali e umane (infanzia, giovinezza, maturità e vecchiaia) alle sei età della lettura mistica cristiana.

Filosofia

Antichità

Il concetto di t. nella filosofia antica si riassume nella definizione di un ordine oggettivo misurabile del movimento. Nella filosofia pitagorica e stoica il t. è concepito come ordine, ritmo del movimento cosmico; nella dottrina platonica invece il t. è misura solo del movimento del mondo materiale della generazione e della corruzione, in cui hanno senso i concetti di passato e di futuro rispetto all’eternità, eterno presente immobile, che compete alla sostanza eterna. Sintesi dei due punti di vista è la definizione aristotelica del t. come «numero del movimento secondo il prima e il poi»: da un lato, infatti, Aristotele, attribuendo movimento circolare, quindi perfetto, ai cieli, accetta il principio pitagorico dell’ordine cosmico come punto di riferimento oggettivo per la misura temporale; dall’altro, distinguendo il mondo dal primo motore immobile, che è fuori del t. e quindi eternamente presente, riproduce lo schema gerarchico di ascendenza platonica.

Nella concezione neoplatonica, da Plotino ad Agostino, permane la distinzione fra t. ed eternità, ma il concetto di t. è collegato, anziché al moto del mondo fisico, all’anima e alla sua vita interna. Escluse le definizioni classiche del t., come moto degli astri e come misura del movimento, non resta ad Agostino che definire il t. come ‘misura dell’estensione dell’anima’, nel ricordo, nell’attenzione e nell’aspettazione (passato, presente e futuro). Sulla linea della critica di Agostino all’idea dei cicli si muovono quegli autori moderni che attribuiscono ai Greci una concezione ciclica del t. storico (teoria dell’‘eterno ritorno’), mentre peculiare del cristianesimo sarebbe una concezione lineare.

Età moderna

La soluzione aristotelica influì profondamente sul pensiero medievale e rinascimentale dove, nonostante le polemiche contro le dottrine fisiche di Aristotele, il concetto di t. rimase pressoché indiscusso. Nella stessa tradizione empirista inglese l’attenzione si concentra sull’accentuazione del carattere mentale della costruzione dell’idea di tempo. Per J. Locke il t. non è connesso solo al movimento ma a qualsiasi ordine costante e ripetibile proprio perché è, come per G. Berkeley, misura della successione (o durata) delle idee nell’intelletto. L’idea di t. si costruisce proprio sulla base del fluire uniforme delle idee nell’intelletto.

Tanto forte rimase il peso della tradizione aristotelica per la definizione del concetto di t. che I. Newton dovette utilizzare, per la sua distinzione fra t. assoluto e t. relativo, di cui solo il secondo rispondeva alla definizione classica di ‘misura del movimento’, il concetto di durata. Già R. Descartes aveva distinto il t., come modo di comprendere, sotto una comune misura, la durata di tutte le cose, dalla durata, come permanere indefinito della realtà. Newton concepisce il t. assoluto (o durata) come una dimensione oggettiva e metafisica che, con lo spazio, contiene gli oggetti naturali e di cui il t. relativo, il t. ‘numero’ della tradizione aristotelica, è «misura sensibile ed estesa mediante il movimento».

Come sul concetto di spazio assoluto, G.W. Leibniz polemizza con Newton anche sul concetto di t. assoluto, contestando il carattere oggettivo di ente metafisico che il t. assume nella interpretazione newtoniana, contrapponendovi una concezione ‘relativa’ del t. in quanto misura di movimenti periodici uniformi, cui si commisurano i movimenti non uniformi; il t. quindi torna a essere identificabile solo con riferimento ai movimenti uniformi esistenti in natura, quali le «rivoluzioni della Terra o degli astri».

Contro ambedue le concezioni polemizza I. Kant, per il quale il t. è, accanto allo spazio, forma pura della sensibilità. Esso è condizione universale e oggettiva di ogni fenomeno in generale perché, a differenza dello spazio, che è forma pura di tutte le intuizioni esterne, essendo il t. condizione formale dell’intuizione interna, vale per ogni fenomeno che entri a far parte dell’esperienza. Per determinare oggettivamente l’ordine di successione nel t. è necessario per Kant che la relazione fra i due stati (il ‘prima’ e il ‘poi’), successivi nella percezione, risponda a una regola per la quale l’avvenimento successivo segua sempre e necessariamente il precedente e il t. risulti quindi irreversibile: questa regola è il concetto del rapporto di causa ed effetto. Il t., come ordine di successione, viene così ridotto da Kant all’ordine causale, secondo un principio che avrà grande fortuna nell’epistemologia moderna fino ad A. Einstein e H. Reichenbach.

Età contemporanea

Completamente diversa da quelle finora esposte è la concezione del t. di H.-L. Bergson. Per Bergson il t. della scienza è una schematizzazione e spazializzazione del t. vero che, come t. vissuto, altro non è che la durata della coscienza. Il t. vero è un fluire non spazializzabile di stati della coscienza in cui non ha senso la distinzione del prima e del poi e, quindi, il concetto d’irreversibilità. Il t. della coscienza è composto di momenti indistinguibili che trapassano l’uno nell’altro, si mescolano e costituiscono un tutto unitario, in cui ogni istante è assolutamente nuovo e insieme si conserva, costruendo la ‘valanga’, via via ingrossantesi, della memoria. Questo t. non spazializzato, che è la dimensione principale della coscienza come fluire ininterrotto e come slancio vitale, è quindi l’oggetto privilegiato di quella intuizione, organo irrazionale o sovrarazionale specifico della filosofia, che Bergson contrappone all’intelletto, organo della scienza, destinato a cogliere l’immobilità della materia, puro meccanismo.

Diverso il discorso di M. Heidegger sul t., nodo centrale dell’analitica esistenziale delineata in Sein und Zeit. Invece che fornire una definizione o una caratterizzazione più o meno complessa della nozione, Heidegger considera il t., o meglio, la temporalità, nelle sue tre dimensioni del passato, del presente e del futuro, come la caratteristica essenziale e costitutiva di quell’ente che è l’«esserci» (Dasein), cioè dell’uomo in quanto essere ‘gettato’ nel mondo e, come tale, legato al passato non meno che al presente, ma anche proiettato nel futuro attraverso la progettualità e le possibilità che gli sono proprie.

Fisica

Il t. è un concetto primitivo in base al quale gli eventi sono distinti in presenti, passati e futuri e coordinati in organica successione. La nozione di t. è legata a quella di cambiamento, in particolare di moto (successione di eventi spazio-temporali relativi a un corpo mobile); la grandezza che ha origine dal concetto primitivo è assunta come fondamentale in tutti i sistemi di unità di misura. A un coordinamento nel t. degli eventi si perviene solo avendo fissato un sistema di misurazione del t., cioè una origine, un verso positivo e un’unità di misura.

Misurazione del tempo

L’unità di misura tradizionalmente si sceglie riferendosi a fenomeni accessibili a tutti e il più possibile invariabili, per es. la rotazione della Terra (si parla di t. terrestre in contrapposizione, per es., al t. siderale o al t. solare). Ogni sistema di misurazione del t. si può rappresentare in un sistema geometrico di ascisse su una retta per cui a ogni evento corrisponde un punto della retta, e viceversa. L’ascissa del punto corrispondente a un evento si chiama ascissa temporale dell’evento o istante (o t.) attuale o t. (dell’evento) e si indica con t. L’origine delle ascisse corrisponde a quella dei t. (istante iniziale o t. zero). Agli eventi posteriori all’istante iniziale si attribuisce ascissa positiva, a quelli anteriori ascissa negativa. Si definisce intervallo di t. la differenza fra due valori del t. (cioè due istanti). Nella fisica classica si postula, con I. Newton, l’esistenza di un t. assoluto che «fluisce uniformemente e senza rapporto con alcun corpo esteriore». Tale visione non ha resistito alla critica di A. Einstein: Newton supponeva sempre possibile stabilire la contemporaneità tra due eventi o se uno (e quale) fosse antecedente. Alla luce di una definizione operativa di simultaneità, ciò è vero per eventi che avvengano nello stesso luogo, ma non se essi accadono in luoghi diversi; il concetto di t. risulta così non assoluto, ma relativo a un osservatore e la variabile t. va trattata, per trasformazioni del sistema di riferimento, come quelle spaziali.

In particolare, si ha il fenomeno della dilatazione del t., per cui un processo fisico ha durata minima nel sistema di riferimento in cui il corpo che lo subisce è in quiete (il t. misurato in tale sistema è detto t. proprio, o t. locale, o t. proprio del sistema di riferimento); se però la velocità relativa tra due osservatori è molto piccola rispetto a quella della luce, la differenza fra le misurazioni effettuate dai due osservatori è in pratica trascurabile (➔ relatività).

La determinazione del tempo

L’espressione determinazione del t. si riferisce alla determinazione del t. dell’orologio (cioè dell’ora), alla determinazione del t. del calendario (cioè della data) e alla determinazione dell’intervallo di t. occupato da un evento (cioè della durata dell’evento medesimo).

La determinazione dell’ora si effettua mediante orologi, in genere meccanici o piezoelettrici e regolati per indicare l’ora civile locale; per determinazioni più accurate si usano orologi di precisione (cronometri), controllati confrontando a regolari intervalli di t., per es., ogni giorno, le loro indicazioni con quelle di un orologio campione o con radiosegnali orari. Per speciali applicazioni si usano anche orologi atomici.

La determinazione della data si riferisce a un sistema di misurazione la cui unità di misura è il giorno e in cui i giorni sono raggruppati a formare periodi più lunghi, i mesi e gli anni; in quasi tutti i calendari l’anno coincide con l’anno tropico (➔ calendario).

Per la determinazione di intervalli di t. dell’ordine delle ore o dei minuti si usano gli orologi ordinari o i contasecondi; per intervalli relativamente brevi, e per determinazioni accurate, si usano cronometri, elettronici se l’intervallo di t. da misurare è molto breve (➔ cronometro).

L’inversione del tempo

L’inversione del t. è l’operazione che varia la direzione di evoluzione del t. per un processo fisico. Molti sistemi sono retti da equazioni che risultano inalterate dopo tale operazione, e in conseguenza sono detti, insieme alle equazioni, invarianti per inversione del t. o per inversione temporale o, anche, reversibili.

In meccanica classica il moto di un sistema con N gradi di libertà è descritto da N coordinate generalizzate (qr(t), r=1, ..., N) che si evolvono con il tempo secondo, per es., le equazioni di Lagrange

con assegnate condizioni iniziali all’istante t0:

In assenza di forze dissipative, la dinamica classica è invariante per inversione temporale. Ciò significa che se, all’istante t1>t0, quando il sistema ha raggiunto la configurazione q1r≡qr(t1), con velocità generalizzate q̇1r≡q̇r(t1), si inverte il segno delle velocità generalizzate e si considera il moto descritto dalle equazioni di Lagrange con le nuove condizioni iniziali:

il sistema evolverà con nuove equazioni orarie q′r(t1), esprimibili in funzione delle precedenti qr(t1), come

e ripercorrerà la medesima traiettoria di prima (all’indietro nel t.).

In meccanica quantistica si può definire, tramite un operatore unitario e antilineare, un’analoga operazione d’inversione temporale per l’equazione di Schrödinger (➔ Schrödinger, Erwin); le interazioni forti ed elettromagnetiche, ma non quelle deboli, sono invarianti per inversione del t. e ciò è descritto mediante i numeri quantici che caratterizzano le particelle elementari (➔).

Mentre le leggi che regolano i processi elementari, nel caso classico e in quello quantistico (a parte le interazioni deboli), sono invarianti per inversione del t., non lo sono i processi termodinamici, relativi a sistemi macroscopici, che sono fondamentalmente irreversibili; ciò è espresso dal fatto che l’entropia di un sistema isolato tende sempre ad aumentare, donde il problema centrale della meccanica statistica di ricondurre l’irreversibilità dei fenomeni macroscopici alle leggi reversibili valide per i processi microscopici (➔ termodinamica).

Unità di misura del tempo

Alla più remota antichità risale l’uso di determinare le date e misurare gli intervalli di t. riferendosi al moto apparente del Sole e delle stelle sulla volta celeste.

Anno solare

Con riferimento al moto apparente del Sole, si definisce anno solare (o tropico) e giorno solare l’intervallo di t. intercorrente fra due successivi passaggi del Sole rispettivamente all’equinozio di primavera (o punto vernale) e al meridiano superiore del luogo di osservazione. Poiché il Sole si muove lungo l’eclittica con velocità variabile, il giorno solare varia durante l’anno; per eliminare il problema che ne deriva nella misurazione del t., si considera un Sole fittizio, detto Sole medio, che percorre con velocità costante l’equatore celeste (non l’eclittica) in un anno tropico. Il giorno solare medio è allora l’intervallo di t. fra due successivi passaggi, al meridiano superiore del luogo d’osservazione, del Sole medio; un anno tropico comprende 365,242198 giorni solari medi. Il giorno solare medio è suddiviso in 24 parti uguali (ore), l’ora in 60 parti (minuti) e il minuto a sua volta in 60 parti.

La 60a parte del minuto è stata assunta come unità fondamentale di misura del t., con il nome di secondo solare medio (o secondo) che è dunque definito come la 86.400ma parte del giorno solare medio. L’origine del t. solare medio si fissa, per ogni giorno, all’istante in cui il Sole medio culmina superiormente, cioè transita al meridiano superiore del luogo d’osservazione (mezzogiorno medio).

fig. 1

fig. 2

T. siderale

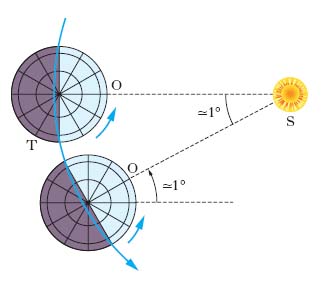
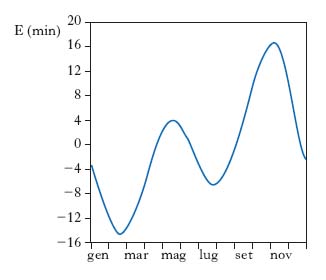
Assai usato dagli astronomi è il t. siderale, ts, definito come l’angolo orario del punto vernale; l’angolo orario ω e l’ascensione retta α di una qualsiasi stella (➔ coordinate) sono legati a ts dalla relazione: ts=ω+α, dove gli angoli ω e α sono misurati in ore, minuti, secondi (1h=15°). Il t. siderale è perciò di facile e accurata determinazione, dovendosi solo osservare il passaggio al meridiano delle stelle fondamentali, di cui è nota l’ascensione retta: per esse risulta, infatti, in tali condizioni, ω=0, sicché è ts=α. L’intervallo di t. tra due successivi passaggi del punto vernale al meridiano, detto giorno siderale, è più corto del giorno solare medio (fig. 1), comprendendo 86.140 secondi solari medi. L’istante di passaggio del Sole al meridiano locale non coincide, in genere, con il mezzogiorno medio; si dice equazione del t. il valore (in minuti e secondi) dell’angolo orario del Sole vero, all’istante del mezzogiorno medio. Essa, differenza tra t. solare medio e t. solare vero (indicato dalle meridiane), varia durante l’anno (fig. 2) e i suoi valori, lievemente variabili di anno in anno, si trovano negli annuari astronomici e nelle tavole di effemeridi nautiche, che riportano anche, per ogni giorno, l’ora siderale a mezzanotte media, il che facilita la conversione del t. siderale in t. medio, e viceversa.

Tempo civile e t. legale

Sia il t. solare (medio e vero) sia il t. siderale sono t. locali, dipendenti dalla longitudine del luogo d’osservazione; il t. medio può differire di vari secondi tra due punti di una grande città e di vari minuti tra due di una stessa nazione. Per evitare l’inconveniente, si è divisa la superficie terrestre in 24 fusi orari, delimitati da meridiani spaziati tra loro di 15°, cioè di un’ora, e si è posto il t., in tutti i punti di uno stesso fuso, pari al t. solare medio t′m del meridiano centrale del fuso (il meridiano centrale del primo fuso orario è quello fondamentale delle longitudini, cioè il meridiano di Greenwich); l’origine del t. è poi fissata non al mezzogiorno medio, ma alla mezzanotte che lo precede (istante zero) ed è questo è il t. civile, pari a t′m+12h. In realtà, la suddivisione in pratica dei fusi orari non segue rigorosamente ovunque l’andamento dei meridiani (➔ fuso) e inoltre in alcune nazioni si adotta talora un t. (t. legale) diverso da quello civile del fuso di appartenenza. Il t. civile, tc, coincide, a meno di 12 ore esatte, con il t. solare medio, t′m, solo per i punti appartenenti al meridiano centrale di ogni fuso; per gli altri esso ne differisce di una quantità pari alla loro longitudine λ rispetto al meridiano centrale, assunta positiva o negativa a seconda che ci si trovi a ovest o a est rispetto ad esso. Tenendo conto anche della differenza tra t. solare medio e vero, si ha che il Sole transita al meridiano di un luogo (e quindi raggiunge la massima altezza sull’orizzonte) all’istante di t. civile dato dalla relazione tc=12h+λ+E, dove E rappresenta l’equazione del t. e λ è misurata in minuti e secondi. Anche in un paese poco esteso in longitudine come l’Italia, a causa della differenza di longitudine e dell’equazione del t., t. civile e t. solare vero possono essere molto diversi, anche a fini pratici; per es., ai primi di novembre, il mezzogiorno vero si ha intorno alle 12h16m a Catania, circa alle 12h04m a Brindisi, circa alle 12h45m a Torino.

Poiché ci si deve riferire a una stessa determinazione di t., sia a fini pratici (per es., orari di voli) sia scientifici (per es., questioni geofisiche), si assume come t. universale (TU, temps universel, e UT, universal time) il t. medio di Greenwich (GMT, Greenwich mean time), cioè il t. civile del fuso orario centrato sul meridiano fondamentale. Nel 1956 si è distinto l’UT in UT0 (UT dedotto immediatamente dalle osservazioni), UT1, (UT0 corretto dall’influenza del moto del polo terrestre) e UT2 (UT1 corretto dalle variazioni della rotazione terrestre dovute a spostamenti di masse d’aria nell’atmosfera); l’unità di t. legata all’UT2 è il secondo medio. Il difetto di uniformità della scala UT, per deformazioni elastiche della Terra e accumulo di aria sui continenti in inverno, è dell’ordine di 10−7.

Strumenti di misurazione

Dal 17° sec. fino a poco tempo fa, gli strumenti per misurare, conservare e controllare il t. erano gli orologi (o pendoli) astronomici, orologi a pendolo atti ad assicurare uniformità di funzionamento (➔ orologio); di solito negli osservatori astronomici vi erano almeno un orologio a pendolo a t. medio e uno a t. siderale. Dagli anni 1930 si usarono orologi piezoelettrici e il confronto fra le loro indicazioni e le osservazioni dei passaggi di astri al meridiano evidenziò piccole differenze, dovute a irregolarità della rotazione terrestre, che rendevano non univoco il giorno solare medio e quindi il secondo solare medio. Si propose perciò di riferirsi a un Sole fittizio, quello medio dell’anno tropico 1900, il cui moto apparente è stato fissato in relazione ad accuratissime effemeridi del moto apparente del Sole vero; al t. solare medio si è sostituito il t. delle effemeridi, la cui unità di misura, detta secondo, fu adottata nel 1956 dal Comitato internazionale dei pesi e delle misure come la frazione 1/31.556.925,9747 dell’anno tropico 1900. L’introduzione di questo secondo (detto anche secondo di t. fisico o di t. atomico), su cui sono regolati tutti gli orologi, e in particolare quelli che controllano le stazioni irradianti radiosegnali orari, ha evidenziato la differenza tra lo scorrere uniforme del t. degli orologi atomici e il non uniforme succedersi di giorno e notte, governato dal t. UT1 delle effemeridi.

Poiché la vita civile è ritmata sui cicli solari del giorno e dell’anno, la scala UT va conservata e raccordata a quella basata sul t. atomico (TAI, temps atomique international, o IAT, international atomic time), per mezzo del sistema detto t. universale coordinato (UTC); che è la scala di t. atomico cui all’istante iniziale del 1° gennaio e, se serve, del 1° luglio di ogni anno, si fanno subire aggiustamenti discontinui di secondi, positivi o negativi (secondi intercalari). Nella pratica, il t. atomico internazionale è formato dal BIH (Bureau international de l’heure) in base alle letture di orologi atomici, sparsi nel mondo in vari laboratori e osservatori e confrontati ogni giorno con metodi radioelettrici e talora con trasporto di orologi atomici.

fig. 3

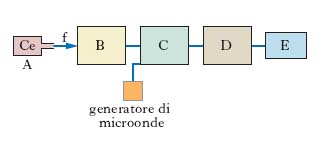
Per realizzare il campione atomico di t. si sfrutta il fatto che l’atomo di cesio ha diverso comportamento magnetico in corrispondenza ai due livelli considerati nella definizione di secondo; sottoponendo gli atomi a un campo magnetico molto disomogeneo, si separano gli atomi che si trovano nei due livelli. Un fascio di atomi neutri di cesio, f, è generato nella sorgente A (fig. 3); il selettore magnetico B fa entrare nella cavità C solo gli atomi nello stato a energia maggiore tra quelli che danno luogo alla transizione che interviene nella definizione di secondo; la cavità è sede di microonde con frequenza (aggiustabile) prossima a quella caratteristica della transizione e stimola (in funzione della frequenza) transizioni degli atomi di cesio verso lo stato a energia minore; l’analizzatore magnetico D fa giungere nel rivelatore E solo gli atomi che hanno subito la transizione. Alla risonanza, il periodo delle microonde moltiplicato per 9.192.631.770 è pari alla durata di 1 secondo. In altri tipi di campione atomico la selezione e l’analisi degli atomi di cesio si effettuano con metodi ottici.

Locuzioni particolari

Il t. di risposta di un’apparecchiatura, per es. di uno strumento di misura o di un dispositivo elettronico, è l’intervallo di t. dopo il quale, in corrispondenza all’applicazione di un segnale a gradino, lo scostamento dal valore di regime del segnale di uscita è inferiore a una quantità prefissata. Il t. di salita e il t. di assestamento sono grandezze rappresentative del comportamento nel tempo di un servosistema (➔) lineare. Il t. di volo è l’intervallo di tempo che una particella impiega a percorrere una base di lunghezza nota (dalla sua misurazione si risale alla velocità della particella).

La variabile temporale è il t. stesso, quando compare nelle equazioni che esprimono le leggi fisiche; la derivata temporale è la derivata rispetto al tempo; l’evoluzione temporale di un sistema è la variazione dello stato del sistema in funzione del tempo.

Istruzione

Poco considerato dalla pedagogia tradizionale, il fattore t. ha assunto rilievo sempre maggiore nella ricerca educativa contemporanea. Tale fattore viene considerato con riguardo sia alle condizioni e fasi dell’apprendimento sia alle procedure dell’insegnamento sia infine alle modalità organizzative dei corsi di istruzione. Con riguardo al primo aspetto, è stata presa in esame l’evoluzione dell’apprendimento in funzione del t. dedicato a un particolare contenuto. Attraverso una metodologia in cui le unità di apprendimento sono ordinate in modo che non si passa alla successiva se la precedente non risulta acquisita, si riesce a far diminuire i t. anche per gli allievi più deboli.

Sul versante dell’insegnamento si sono puntualizzate specifiche strategie, quali quelle dell’istruzione programmata (➔ istruzione) e del mastery learning (➔), che trovano la loro naturale sede d’incontro nell’organizzazione dei corsi di studio svolti dalle istituzioni scolastiche. Il fattore t., in questo caso, entra in considerazione a più livelli: anzitutto, si riflette sulla durata complessiva della formazione scolastica, nonché delle fasi o gradi in cui essa si scandisce. Fino agli anni 1950-60, nella maggior parte dei paesi convivevano due percorsi di istruzione: uno, di durata limitata, diretto a dare una formazione di base prima dell’avvio al lavoro; l’altro, di durata più lunga e destinato a una minoranza, comprendeva più gradi di istruzione fino all’università. Tale situazione dicotomica è superata, grazie anche alla progressiva estensione dell’obbligo scolastico e alla consapevolezza maturata dalle comunità a premere per corsi prolungati di istruzione. Altro tema di rilievo è quello dell’estensione dell’anno scolastico, cioè del numero dei giorni destinati all’attività didattica, diversi da un paese all’altro. Anche sui t. giornalieri di permanenza a scuola vi sono orientamenti differenti: in vari paesi l’orario delle lezioni comprende pure alcune ore pomeridiane, spesso con il sabato libero; altrove sono state introdotte forme organizzative di t. pieno, con prolungamento pomeridiano per attività libere o integrative. Scuola integrata viene comunemente detta quella in cui le attività curricolari e quelle extracurricolari sono equamente distribuite nel corso della giornata scolastica.

In Italia, il t. pieno è stato introdotto nella scuola elementare, in applicazione dell’art. 1 della l. 820/24 settembre 1971, «con lo scopo di contribuire all’arricchimento della formazione dell’alunno», e ha autorizzato forme di lavoro in équipe dei docenti sia delle attività curricolari sia di quelle extracurricolari. Anche nel settore della scuola media si è estesa una sperimentazione di scuola integrata.

Linguistica

Il momento (presente, passato o futuro) in cui si colloca l’azione indicata da un verbo. Questa nozione, che accanto a quella di aspetto verbale (➔), rappresenta la determinazione della nozione più ampia di processo espressa da un verbo, assume rilievo grammaticale nella maggior parte delle lingue, e viene espressa mediante un sistema di forme che costituiscono i t. verbali. Si distinguono t. assoluti, riferiti cioè esclusivamente al parlare (presente, passato, futuro) e t. relativi, riferiti ad altro t. dello stesso periodo sintattico (futuro anteriore, piuccheperfetto); t. semplici, che constano di un solo elemento, variabile secondo il numero e la persona, e t. composti, forniti di uno o più ausiliari, e perciò detti anche perifrastici.

Nel sistema verbale indoeuropeo comune la nozione temporale interferisce con quella dell’aspetto, che risulta predominante, come appare ancora chiaramente rappresentato dal sistema verbale greco, dove il cosiddetto presente indica il processo in via di svolgimento, l’aoristo il processo in sé (azione puntuale), il perfetto il risultato di un’azione compiuta. Il t. trova nell’indoeuropeo la sua prima affermazione grammaticale soprattutto nell’opposizione presente-passato (le forme storiche del futuro sono innovazioni indipendenti nello sviluppo delle singole lingue), si afferma poi nella storia successiva dei diversi sistemi linguistici, e diviene prevalente in alcuni di essi, come, per es., nelle lingue romanze, dove la funzione dell’aspetto è puramente accessoria, mentre la distinzione temporale si articola in un ricco complesso di forme grammaticali.

In grammatica, proposizioni temporali, le subordinate che esprimono una nozione di t.: in italiano sono introdotte dalle congiunzioni quando, allorché, mentre, finché ecc., e dalle locuzioni prima che, dopo che, appena che, e simili, quando hanno forma esplicita, mentre nella forma implicita possono esprimersi con il participio passato (preceduto o no da appena, dopo), con il gerundio, con l’infinito preceduto dalle preposizioni in, a, su o dalle locuzioni prima di, dopo (di).

Meteorologia

Insieme delle condizioni fisiche atmosferiche cioè, più propriamente, lo stato meteorologico (anche chiamato stato del t. o t. meteorologico). È caratterizzato dalle condizioni meteorologiche (temperatura, stato del cielo, umidità, pressione atmosferica, vento ecc.) e viene detto t. locale o t. in grande a seconda che le condizioni siano relative a una regione ristretta o abbraccino una vasta superficie (per es., tutto un continente). La previsione del t. è oggetto della meteorologia (➔).

Musica

Indicazione agogica (➔) che prescrive un movimento più o meno rapido cui attenersi nell’esecuzione d’un pezzo, in genere indicato con didascalie di preciso valore (Adagio, Andante, Presto, Allegro, Vivace ecc.). Di qui il termine è passato a indicare un pezzo che fa parte di una composizione sinfonica, analogamente all’atto nelle produzioni operistiche (il nome deriva dal fatto che ogni parte ha un t., cioè un andamento agogico diverso). Nella sinfonia classica, i t. o movimenti sono, nell’ordine, quattro: Allegro, Adagio, Minuetto (o Scherzo), Finale (l’ordine, a volte, può essere diverso: la nona sinfonia di L. van Beethoven, per es., ha lo Scherzo al secondo posto e l’Adagio al terzo; oppure l’ultimo è un Adagio, come nella sesta sinfonia di P.I. Čajkovskij).

Psicologia

Nell’ambito della ricerca sul problema del t., si devono a P. Fraisse i lavori di maggiore impegno che si sviluppano nelle prospettive della ‘percezione della successione’, della ‘percezione e stima della durata’, e dell’‘orientamento temporale’.

Dal punto di vista psicogenetico, i contributi più rilevanti sono venuti invece da J. Piaget, che ha indicato come il concetto di t. si vada formando parallelamente a quello di spazio in base alla capacità di coordinazione delle velocità. Questi concetti sarebbero inizialmente (e fin verso il settimo anno) di natura essenzialmente visuale, mentre verrebbero successivamente raccolti in un sistema di t. comune che fa concordare il t. fisico (esterno o obiettivo) con quello psicologico (interno o soggettivo).

Religione

T. sacro

La distinzione tra sacro e profano, fondamentale per ogni religione, investendo tutti i settori dell’esperienza umana, come gli oggetti, le persone, le azioni, i luoghi, i racconti ecc., riguarda anche i periodi di tempo. Come per creare un luogo sacro bisogna delimitarlo rispetto allo spazio circostante, così anche per il t. sacro è essenziale la delimitazione dal t. comune. I modi della delimitazione possono essere vari, ma vi è in essi un fondo comune e sostanziale: il t. sacro, per staccarsi nettamente dal t. profano, deve essere diverso da quest’ultimo. È la diversità dagli altri giorni che caratterizza, per es., la festa, che è il caso più tipico del t. sacro, anche se il t. sacro non si limita né si estende necessariamente a una giornata ma può concentrarsi anche su durate minori, per es. quella di un’azione rituale, e può, d’altra parte, occupare periodi molto più lunghi; né il t. sacro presuppone necessariamente un calendario festivo pubblico, e ciò che può essere t. sacro per un determinato gruppo di individui, per es. una famiglia, come momenti di celebrazioni rituali private in occasione di nascite, nozze, morti, anniversari ecc., può non essere festa per altri gruppi della comunità. Per la festa, come per altri tipi di t. sacro, valgono norme differenti da quelle che regolano l’esistenza umana nel t. profano; il modo di questo suo differenziarsi è storicamente condizionato dalle singole forme religiose.

La differenza fondamentale tra t. sacro e t. profano è che quest’ultimo è continuo e irreversibile, mentre il t. sacro è al di fuori della continuità: nel corso dell’anno avvengono i fatti più vari nella vita dell’individuo o della società, che impongono sempre nuove reazioni o sforzi di adeguamento; ma il Natale, per es., in modo perfettamente indipendente da tutti quei fatti, è sempre uguale a sé stesso e richiede sempre lo stesso comportamento, la celebrazione della nascita di Gesù; così, quasi tutte le feste delle più varie religioni hanno un aspetto commemorativo, un legame con un accadimento essenziale avvenuto una volta per sempre, nel mito, nella storia sacra o eventualmente nella storia reale; e nella celebrazione rituale della festa, la società si riconnette alle proprie tradizioni sacre: nel t. sacro rivive, infatti, mediante i gesti e le parole che lo rievocano, il t. del mito, un t. ugualmente ben distinto dal t. storico irreversibile, in quanto in esso quelle tradizioni sono state, una volta per sempre, fondate e rese immutabili.

Nella liturgia latina, il temporale è la parte più importante dell’anno liturgico; ha per centro il triduo pasquale (➔ triduo) e comprende t. di Avvento (con le solennità di Natale ed Epifania), Quaresima (che porta alla Pasqua di Risurrezione) e t. pasquale (con le solennità di Pasqua-Ascensione-Pentecoste). A questi t. forti segue il t. ordinario o per annum.

Scienze sociali

T. libero

La parte della giornata di un lavoratore in cui questo è libero da impegni di lavoro, i cui requisiti fondamentali sono la libertà dalle obbligazioni, il carattere disinteressato e non utilitaristico delle attività svolte nel periodo in cui non si lavora, la ricerca di rilassamento e di gratificazioni.

Il concetto di t. libero è nato con l’affermarsi dei modi di vita tipici della civiltà industriale. Non appare infatti corretto parlare di t. libero, nell’uso oggi corrente del termine, in relazione alle società arcaiche e alle società contadino-artigianali: nel primo caso, come osserva il sociologo J. Dumazedier, «lavoro e gioco erano parte di un solo rituale attraverso il quale gli uomini cercavano la comunione con gli spiriti ancestrali», nel secondo caso, l’intera esistenza, sia nei periodi in cui si lavorava dall’alba al tramonto nei campi sia nei periodi di forzata inattività, si configurava come una continua e drammatica lotta per sopravvivere. Le feste religiose del Medioevo, durante le quali il lavoro era proibito, presentando un preponderante aspetto cerimoniale, non soddisfacevano i fondamentali requisiti di ciò che oggi si dice t. libero. In quanto all’otium delle classi colte delle antiche civiltà occidentali e dell’aristocrazia tardo-medievale e rinascimentale, bisogna osservare che non ha nulla a che vedere con l’odierno concetto di t. libero poiché è impossibile definirlo in relazione a un t. di lavoro, configurandosi piuttosto come sostituto del lavoro.

Nella vita sociale della civiltà industriale, il t. libero assolve ad alcune evidenti funzioni fisiologiche, psicologiche e sociali: consente di riposarsi dalla fatica del lavoro, di vivere una vita più ricca, di scaricare le tensioni accumulate, di evadere dalla routine quotidiana. D’altra parte, si configura anche come ulteriore strumento di controllo sociale tramite il condizionamento di consumi e di modelli di comportamento indotti dall’esterno. Negli studi sociologici da un lato si è sottolineata la straordinaria possibilità di espansione e di realizzazione della personalità umana che la crescente disponibilità di t. libero potenzialmente consente; dall’altro si è posto l’accento sull’eterodirezione consumistica resa possibile dal t. libero e sulla crescente frattura fra lavoro e t. libero. La diffusione delle tecnologie informatiche e delle forme di lavoro telematico, se da un lato contribuisce ad accrescere l’area del t. libero, dall’altro rende sempre più precario il confine con i t. di lavoro, per cui la modificazione del concetto e delle pratiche del lavoro è destinata a ripercuotersi sul concetto e sulle pratiche del t. libero.

Tecnica

Il t. di lavorazione è un parametro significativo nell’ambito dell’organizzazione scientifica della produzione.

Nella tecnica dell’elaborazione elettronica di dati, si indica con l’espressione in t. reale (calco dell’ingl. in real time) la circostanza per cui i dati d’ingresso sono i valori attuali delle grandezze d’ingresso e i risultati dell’elaborazione sono resi disponibili prima che siano intervenute variazioni sensibili in tali valori.

In un processo tecnologico, in un dispositivo di misura ecc., è detto t. morto il rapporto, di solito percentuale, fra il t. di attesa e il t. totale di funzionamento.

Nel ciclo di funzionamento di un motore termico, si dice t. ciascuna delle trasformazioni che subisce il fluido motore: motore a due t., a quattro t. (➔ motore).