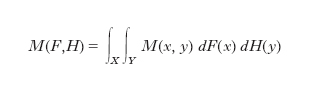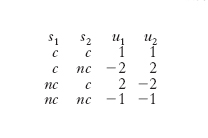gioco

Esercizio singolo o collettivo a cui si dedicano bambini o adulti, per passatempo, svago, ricreazione, o con lo scopo di sviluppare l’ingegno o le forze fisiche. Anche, pratica consistente in una competizione fra due o più persone, regolata da norme convenzionali, e il cui esito, legato spesso a una vincita in denaro (posta del gioco), dipende in maggiore o minore misura dall’abilità dei contendenti e dalla fortuna.

Antropologia

Il g. come forma di svago ha avuto importanza storica e antropologica in ogni epoca e cultura, come evidenziato da autori quali J. Huizinga (1939) e R. Caillois (1958); ma oltre al lato puramente ludico il fenomeno del g. presenta una grande varietà di aspetti e possibili approcci – sociologico, filosofico e psicanalitico – fino a diventare una forma di situazione tipica della realtà quotidiana.

Varietà di significati

All’interno di una stessa area geografica o nel passaggio da una cultura a un’altra il g. può subire profonde variazioni, passando da funzioni rituali o religiose a semplice intrattenimento, per es., gli indovinelli, documentati in Grecia in età anteriore al 5° sec. a.C. come sfida con esito anche mortale, o il labirinto, che nel Medioevo cristiano riproduceva i percorsi dei pellegrinaggi religiosi, mentre già nel Rinascimento era ridotto a elemento decorativo di giardini. Una possibile classificazione dei g. è quella che li suddivide in g. d’azzardo, di competizione, di simulacro o di ruolo (➔), di vertigine o provocazione: alcuni g. di società infatti comportano penitenze e pegni da parte di chi perde; sono anche chiamati jeux idiots quelli che hanno come fine quello di creare imbarazzo o disagio nei partecipanti (g. della verità, passatella, g. della torre) o il metterne a repentaglio l’incolumità fisica (roulette russa). Uno stesso g. può avere, in ambiti diversi, differenti fini: il ripiglino, diffuso in Europa come g. infantile, ha presso molti popoli (Inuit, Australiani) valore comunicativo e artistico; il g. dell’aquilone ha conservato a lungo funzioni apotropaiche in Corea.

Giochi per bambini e giochi per adulti

G. individuali e collettivi ancor oggi in uso tra i bambini (altalena, aquilone, palla, nascondino) sono documentati già nel mondo greco-romano (agevole il passaggio da questa tipologia di g. a quelli in cui preponderante è l’attività fisica e atletica di chi lo pratica, gli sport). Erano propriamente destinati agli adulti il g. del cottabo, della morra, degli astragali (quest’ultimo, considerabile anche come g. d’azzardo, consisteva essenzialmente nel lancio di ossicini astragalici, facilmente reperibili nell’ambito di un’economia pastorizia, che in base a come si disponevano dopo la caduta assumevano valori e significati differenti).

Nel Medioevo furono diffusi giochi con dadi (zara) e altri strumenti (dischi, birilli, trottole). Molto comuni erano anche gli scacchi e i g. di carte: i tarocchi, scopa, briscola ecc.

Nell’Ottocento ebbero successo i g. di società, di vario tipo: g. di destrezza, di movimento, di parole, di cui alcuni sopravvivono nei quiz televisivi e nei periodici enigmistici.

Giochi da tavola

Ma fra tutti, i g. più antichi, diffusi e ramificati sono i g. da tavola, nei quali i giocatori muovono pezzi, pedine o segnaposto su un apposito ripiano (tavoletta, tabellone, plancia, o, con nome specifico, scacchiera, damiera) eseguendo, con l’ausilio o no di dadi, mosse o spostamenti che, in base alle caselle che di volta in volta vengono a essere occupate, impongono o consentono determinate azioni stabilite dalle regole (cattura o perdita di pezzi, soste, penalizzazioni, pagamenti ecc.).

Le testimonianze più antiche di attività simili riguardano il g. del mancala (scavi di Ain Ghazal, 7000-5000 a.C., attestato anche in Egitto, 1400-1300 a.C.), tuttora diffuso in Africa e in Asia. Il mancala è un g. di calcolo aritmetico e si pratica fra due persone, muovendo sassolini, semi o altro su una superficie fornita di un numero variabile di buchi. Ancora in Egitto (2600 a.C. ca.) è attestato un g. di percorso a spirale, paragonabile al g. dell’oca, diffuso in Europa a partire dal 1580, ma con alcune caratteristiche simili anche al g. della rinascita tibetano e al g. della promozione dei mandarini cinese, entrambi sicuramente anteriori a tale data.

Alla prima dinastia di Ur (dopo il 2650) risale il cosiddetto g. reale di Ur, ora conservato al British Museum. È probabile che sia un archetipo del tabula (detto anche alea) romano; di questo conosciamo le regole con cui lo giocava l’imperatore Claudio e, attraverso le tables medievali e il tric-trac settecentesco, possiamo seguirne le trasformazioni sino all’attuale backgammon. L’evoluzione dell’attuale dama passa da un g. diffuso in Egitto dal 1400-1300 attraverso l’alquerque, estremamente popolare nel Medioevo arabo e spagnolo. Piuttosto complessa è la storia degli scacchi. Della cultura cino-giapponese è il g. del go, diffuso in occidente da pochi decenni e considerato dagli specialisti il più raffinato dei g. di tavoliere. Per le culture extraeuropee è fondamentale il problema dei possibili rapporti fra l’azteco patolli, sicuramente precolombiano, e il pachisi, attestato in India almeno dal 1542-1605 d.C., e giocato su un tavoliere di stoffa, con ricamata una scacchiera a croce, lungo la quale si spostavano le pedine, in base al lancio di particolari dadi, verso il traguardo finale. Il pachisi fu trapiantato in Inghilterra verso il 1880 con il nome di ludo.

Con la nascita, negli Stati Uniti, nel 1935, del monopoly, importato in Italia, con il nome di monopoli, nel 1936, nasce il moderno g. in scatola, con fini consapevolmente merceologici.

I g. di simulazione strategica, discendenti dei g. con i soldatini, nascono nelle scuole di guerra prussiane e la loro diffusione si ha con i board war games, nati in ambiente angloamericano tra il 1953 e il 1962. I board war games portarono alla moltiplicazione dei g. di simulazione strategica che approdarono, con Dungeons and dragons (1974) ai g. di ruolo e ai game books. Sebbene la creazione dei videogiochi abbia ristretto la diffusione dei g. di tavoliere tradizionali, ne sopravvivono alcuni, più o meno vecchi, come il Reversi (1888, dal 1977 in Italia con il nome di Othello), lo Scrabble (1949, in Italia dal 1955 col nome di Scarabeo), Cluedo (1949), La conquête du monde (1961, Risiko in Italia dal 1977), Master mind (1972), Trivial pursuit (1979). Dai g. di tavoliere nascono infine complessi rompicapo, come il cubo di Rubik (1978).

Videogiochi

Il mercato del g. è oggi largamente dominato dai videogiochi, intendendo con questo termine qualunque tipo di g. che venga eseguito con un computer, sia domestico sia tascabile sia da sala-giochi. La storia dei videogames ebbe inizio nel 1962 presso il Massachusetts Institute of Technology, quando lo studente S. Russel scrisse il programma di un g. chiamato Spacewar su un computer della Digital Equipment; Space;war si diffuse rapidamente e passò da un college a un altro. Negli anni successivi un altro studente N. Bushnell, dell’università dello Utah, ne mise a punto una versione funzionante a monetine; l’esperienza lo spinse poi a intraprendere un ulteriore progetto, per il quale fondò una nuova società, oggi famosissima: l’Atari, la quale lanciò una versione elettronica del ping-pong, denominata Pong, che ebbe subito grande successo. Nel 1978 si realizzò il vero lancio commerciale dei videogames, con Space Invaders, prodotto offerto dalla giapponese Taito. Tre anni dopo arrivò dal Giappone un nuovo g., offerto dalla Namco, il cui protagonista, un curioso personaggio dalla testa gialla e con una grande bocca, divorava dei fantasmi che gli intralciavano il cammino: il suo nome era Pac-Man, nome di quello che ancor oggi è il più venduto videogame di tutti i tempi.

I videogames della prima generazione presentavano un problema fondamentale: l’assenza di una reale possibilità di modifica dei parametri del g., soprattutto riguardo alla loro migrazione su macchine diverse da quelle a logica cablata per le quali erano nati. L’improvvisa esplosione del personal computing agli inizi degli anni 1980 aprì definitivamente la strada alla commercializzazione su scala planetaria dei videogames, facendoli uscire dalle sale-giochi e diffondendoli in modo capillare.

Diritto

Il g. e la scommessa possono rilevare per il diritto civile in tre modi differenti: può trattarsi di un fenomeno protetto, quando sono non solo leciti, ma anche fonte di un rapporto giuridico obbligatorio (i g. che addestrano al maneggio delle armi, le corse di ogni specie e ogni altra competizione sportiva, in base all’art. 1934 c.c., nonché le lotterie debitamente autorizzate, in base all’art. 1935 c.c.); in questi casi g. e scommessa rilevano come contratti aleatori (➔ alea). Può altresì trattarsi di un fenomeno meramente permesso, quando non rientri nei casi previsti dall’art. 1934 c.c. ma non sia neppure vietato dall’ordinamento; in tal caso g. e scommessa costituiscono attività lecite che non fanno sorgere un rapporto giuridico obbligatorio, ma la più limitata conseguenza di impedire che chi abbia spontaneamente pagato il debito di g. possa chiedere la restituzione di quanto versato (art. 1933 c.c.), a meno che non vi sia stata frode o che il perdente sia un soggetto incapace di agire. G. e scommessa possono infine essere proibiti quando sono illeciti, ossia riprovati dall’ordinamento. In questo caso i contratti di g. e scommessa sono nulli.

A norma dell’art. 721 c.p. è definito gioco d’azzardo il g. nel quale ricorre il fine di lucro e la vincita, o la perdita, è quasi interamente aleatoria. Sono pertanto case di g.  i luoghi di convegno destinati al g. d’azzardo, anche se privati, e anche se lo scopo del g. è sotto qualsiasi forma dissimulato. L’esercizio del g. d’azzardo integra una contravvenzione, punibile con l’ammenda e con l’arresto e implicante la pubblicazione della sentenza, nonché la confisca del denaro esposto nel g. e degli arnesi od oggetti a esso destinati. Se il colpevole è un contravventore abituale o professionale, alla libertà vigilata può essere aggiunta la cauzione di buona condotta. Posti tali criteri, sono stati ritenuti g. d’azzardo gli apparecchi automatici (cosiddette slot-machine), il ramino, il poker, la zecchinetta, il bacarà, il sette e mezzo, il domino, il cun-cain, il g. dei dadi, la riffa, la roulette, la tombola e la briscola. Controversa è l’aleatorietà del g. delle carte e similari.

Imposta unica sul gioco

Istituita con la l. 1379/1951 (che ha introdotto l’imposta unica sui g. di abilità e sui concorsi pronostici), è attualmente disciplinata dal d. legisl. 504/1998, emesso in attuazione della l. 3 agosto 1998, che ha riordinato la disciplina. Essa riguarda esclusivamente i concorsi pronostici e le scommesse. I soggetti passivi dell’imposta sono individuati in tutti coloro che gestiscono, delegati dallo Stato o in concessione, l’organizzazione e l’esercizio del g. sul quale si svolgono concorsi pronostici e scommesse. Per le scommesse sportive e ippiche, i soggetti passivi del tributo sono il Comitato Olimpico Nazionale Italiano (CONI) e l’Unione Nazionale Incremento Razze Equine (UNIRE). Sono previste distinte modalità di computo della base imponibile e aliquote di diversa misura a seconda che si tratti di giochi prognostici o di scommesse. In particolare, nel caso dei concorsi pronostici la base imponibile è costituita dall’intero ammontare della somma corrisposta dal concorrente per il g., al netto di diritti fissi e compensi ai ricevitori. Nel caso delle scommesse, invece, la base imponibile è determinata dall’ammontare della somma giocata per ciascuna scommessa. Sebbene sia assolta dagli enti che organizzano il g., l’imposta sul g. è destinata a essere traslata sui giocatori.

Matematica

La teoria dei g. (➔ giochi, teoria dei) ha avuto origine nell’ambito dell’economia (per la sua elaborazione fu premiato con il Nobel J.F. Nash), ma si è poi ampiamente sviluppata nell’ambito matematico, sulle basi del calcolo delle probabilità, soprattutto in relazione alla ricerca operativa. In essa sono prese in considerazione le situazioni di competizione o di conflitto, in cui a determinare il risultato concorrono le azioni di due o più persone (o gruppi di persone), dette giocatori, con interessi contrastanti, più, eventualmente, il caso. Tipici esempi di tale situazione sono i g. di carte, in cui norme precise fissano le possibili azioni dei giocatori, il ruolo del caso, e il risultato che ne deriva; ma le applicazioni della teoria dei g. hanno un campo molto più vasto, pur con le inevitabili inesattezze derivanti dal costringere una situazione reale in uno schema matematico: in economia, nell’industria, in situazioni militari ecc.

La principale caratteristica dei g. è che ciascun giocatore conosce le possibili azioni degli altri giocatori (con i risultati che ne conseguono), ma non sa quale sarà la loro scelta: di qui la difficoltà della decisione. In generale in un g. ciascun giocatore è chiamato a fare più ‘mosse’ successive. Si può però immaginare che un giocatore decida fin dall’inizio quali scelte fare nel corso del g., tenendo conto delle situazioni che si possono presentare. La linea d’azione così fissata prende il nome di strategia. Se nel g. vi sono scelte che dipendono dal caso (per es., la distribuzione delle carte nel poker), si valuta il risultato mediante il suo valore medio; questo procedimento, che sarebbe criticabile, si giustifica ricorrendo al concetto di utilità del risultato per il giocatore. Se vengono indicate le possibili strategie dei vari giocatori, e i risultati che ne derivano, il g. si dice in forma normale, in contrapposizione alla rappresentazione ad albero, o estensiva, che indica per ogni mossa le diverse alternative.

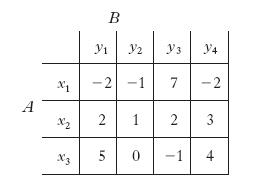
I g. per cui la teoria è più semplice e meglio sviluppata sono quelli di due giocatori a somma nulla, cioè tali che quello che perde un giocatore viene vinto dall’altro e viceversa, senza pagamenti verso l’esterno o dall’esterno. In tal caso basta indicare le vincite (o perdite) di un giocatore; quelle dell’altro giocatore sono l’opposto. Una tipica rappresentazione di un g. in forma normale si ha mediante la tabella (o matrice) dei pagamenti, come quella rappresentata, in cui x1, x2, x3 sono le strategie del giocatore A e y1, y2, y3, y4 le strategie di B; agli incroci delle righe con le colonne sono riportate le vincite (le perdite se il numero è negativo) di A, che sono insieme le perdite (o le vincite) di B:

In alcuni g. un giocatore ha una strategia ottima. Tra questi vi sono i g. a informazione perfetta, in cui a ogni mossa i giocatori conoscono tutte le scelte precedenti: per es., negli scacchi un giocatore (o un elaboratore elettronico) che potesse prendere in considerazione tutte le strategie possibili, troverebbe la strategia ottima. Ma in molti g., come è evidente in quello della tabella, nessuno dei due giocatori ha una strategia migliore delle altre in senso assoluto. Esiste però nella tabella un valore (1, corrispondente alle strategie x₂ e y₂) che è insieme il minimo della sua riga e il massimo della colonna. Si dice allora che il g. ha un punto di sella o che ha il minimax (x₂ e y₂ sono dette allora strategie minimax), ed esistono validi motivi che consigliano la scelta della strategia minimax. Infatti A, scegliendo x₂ si assicura comunque la vincita 1; potrebbe aspirare a un risultato migliore, ma sa che B, scegliendo y₂, può costringerlo ad accontentarsi di vincere 1, e metterlo anzi a rischio di ottenere un risultato peggiore; inoltre la scelta di x₂ è l’unica che non lo danneggia se B in qualche modo riesce a conoscerla o prevederla. Così, la scelta della strategia minimax, se esiste, si impone, non essendovi una strategia migliore in senso assoluto.

Quando in un g. non esiste il minimax, per cercare una soluzione al problema occorre ricorrere a una scelta casuale che consiste nello scegliere a caso la strategia (per es., lanciando dei dadi, o delle monete ecc.) dopo aver scelto in modo opportuno le probabilità delle singole strategie. In questo caso la scelta del giocatore consiste nel fissare le probabilità delle strategie (ciò viene detto strategia mista, chiamando strategie pure quelle considerate finora), mentre la scelta definitiva della strategia è fatta dal caso. Osserviamo che si hanno g. in cui le strategie possono variare in modo continuo: in essi, sia A sia B hanno a disposizione infinite strategie e la tabella dei guadagni viene sostituita da una funzione M(x, y) che per ogni strategia x di A e y di B dà la vincita di A. La soluzione ottimale è allora di solito rappresentata da una strategia mista, che si può precisare, come tra poco verrà chiarito, mediante due opportune funzioni.

Per l’impostazione matematica, un g. G=(X, Y, M) viene caratterizzato mediante l’insieme X delle strategie x del primo giocatore, l’insieme Y delle strategie y del secondo giocatore, e la funzione dei pagamenti M(x, y). Se X e Y sono insiemi appartenenti a spazi euclidei, le strategie miste possono essere individuate mediante funzioni di ripartizione, F(x) per il primo giocatore e H(y) per il secondo, tali che F₀(x) [o G₀(y)] sia uguale alla frequenza relativa delle strategie di A [B] comprese tra le strategie 0 e x [0 e y]. La funzione dei pagamenti è data allora dall’integrale di Stieltjes:

Se per il g. G si calcolano i valori

l=sup_x inf_y M(x, y), n=inf_y sup_x M(x, y),

è sempre l≤n: se l=n si dice che il g. ha minimax, e v=l=n viene detto valore del gioco. Se v’è una strategia x₀ tale che infM(x₀, y)=v, essa si dice strategia minimax; analogamente per il secondo giocatore. Il teorema fondamentale della teoria dei giochi assicura che, sotto condizioni molto ampie, ricorrendo alle strategie miste il g. ha sempre il minimax. La sua dimostrazione, già rintracciabile in molti autori (in particolare F.-É.-É. Borel), è stata riottenuta in forma più completa da J.L. von Neumann.

Sono stati studiati sistemi in cui le scelte possibili per ogni decisore sono quella di cooperare (c) e quella di non cooperare (nc), e l’utilità del decisore che ha cooperato mentre qualcun altro non cooperava è molto bassa. Consideriamo, per es., il g. in cui l’utilità di due decisori è fissata dalla seguente tabella deterministica:

dove s₁ e s₂ sono rispettivamente le scelte del primo e del secondo decisore, e u₁ e u₂ sono le loro utilità. È allora chiaro che, non appena uno dei giocatori decide di non cooperare, anche l’altro smette di farlo e il sistema si porta stabilmente nello stato (nc, nc), che, sebbene abbia un’utilità minore dello stato (c, c) per entrambi i decisori, è uno stato stabile.

La teoria dei g. è sorta, come già si è accennato, nell’ambito dell’economia e ha avuto i suoi primi sviluppi dalla collaborazione tra il matematico J.L. von Neumann e l’economista O. Morgenstern (Theory of games and economic behavior, 1944). In tale ambito essa ha come principale oggetto lo studio delle circostanze connesse al rischio delle decisioni economiche. I problemi vantaggiosamente studiati mediante la teoria dei g. sono quelli in cui l’utilità di ciascuno dipende dal comportamento di tutti gli altri operatori; innanzitutto le situazioni di concorrenza oligopolistica, irrisolvibili con gli strumenti della microeconomia neoclassica.

Psicologia

Il g. acquista significati diversi in relazione all’età, al sesso, ai contesti culturali. L’interesse di psicologia e pedagogia quasi esclusivamente per il g. nell’età infantile si spiega con l’indubbia rilevanza di esso nei processi di orientamento, definizione e sviluppo delle funzioni percettivo-motorie, mentali e sociali caratteristici di detta età. Le teorie sul g. evidenziano soltanto aspetti particolari, che tuttavia risultano utili alla comprensione di un fenomeno complesso e di non facile definizione. Con riferimento alla teoria biogenetica di E.H. Haeckel, è stata proposta una spiegazione ‘ancestrale’ del g. (G.S. Hall), per cui il bambino adotterebbe via via tipi di g. che rispecchiano nel medesimo ordine le attività espresse dall’uomo nel corso dell’evoluzione della specie. Secondo altri, il g. sarebbe il mezzo mediante cui il bambino sprigiona l’eccesso di energia psichica accumulata (H. Spencer) ovvero costituirebbe una forma di ‘esercizio preparatorio’ delle attività del soggetto adulto (E. Claparède, K. Gross) oppure una specie di ‘esercizio complementare’ atto a confermare abitudini utili, ma tendenti a estinguersi se non esercitate nell’attività ludica (H. Carr). Secondo la ‘teoria catartica’ (S. Freud, A. Adler) il g. avrebbe la funzione di liberare l’individuo da tendenze o istinti incompatibili con le esigenze della vita sociale. Altri hanno pensato al g. come fattore di conoscenza, di esperienza, di rinforzo, di divertimento ecc.

Con particolare attenzione allo sviluppo dell’intelligenza infantile, J. Piaget ha riscontrato un parallelismo fra le modalità che il g. assume nelle diverse fasi dell’età evolutiva e le caratteristiche dei processi psico-motori e mentali manifestate dal bambino nelle stesse fasi della sua crescita. La psicopedagogia è incline a pensare che il g. risponda contestualmente a molteplici esigenze e svolga una funzione fondamentale nello sviluppo equilibrato del bambino.

La principale caratteristica delle ricerche psicologiche degli ultimi decenni del 20° sec. è la rinuncia a una spiegazione unitaria ed esaustiva del significato psicologico del gioco. In gran parte per l’influenza dei risultati dell’etologia, viene riconosciuta l’esistenza di forme distinte di g.: ciascuna di esse assolverebbe diverse funzioni psicologiche, utili alla crescita fisica e psichica dell’individuo, oltre che all’adattamento e alla sopravvivenza della specie. La psicologia ha evidenziato come le varie forme di g. infantile siano finalizzate a sviluppare e strutturare i meccanismi di autocontrollo delle funzioni senso-motorie e cognitive: saltare, fare le capriole ecc., permettono di autoregolare le funzioni motorie; g. ripetitivi, come tirare la palla in un canestro, consentono di affinare la coordinazione senso-motoria attraverso processi di retroazione e correzione che divengono gradualmente automatici; la manipolazione e la costruzione di oggetti favoriscono l’impiego di schemi mentali e dell’immaginazione; il g. di finzione (gli oggetti assumono funzioni e ruoli simbolici: per es., un oggetto d’uso ordinario che si trasforma in astronave) contribuisce a sviluppare le funzioni simboliche, come avevano già messo in evidenza Piaget, L.S. Vygotskij e J.S. Bruner; infine, i g. di gruppo e i g. sociali attivano le relazioni interpersonali, i ruoli e le gerarchie.

Un’area della psicologia del g. riguarda la diffusione dei videogiochi. Oltre ai problemi relativi agli effetti di alcuni di essi sul piano emozionale (quando, per es., evochino comportamenti aggressivi e violenti), la psicologia studia l’interazione bambino-videogioco anche sul piano dei processi cognitivi. L’attenzione, la memoria e il ragionamento possono risultare particolarmente impegnati. Inoltre, i videogiochi possono svolgere un ruolo psicosociale e psicopedagogico quando sia prevista l’interazione tra più bambini per cooperare allo svolgimento del gioco.

Zoologia

Il g. è un’attività di notevole importanza nei processi di sviluppo di molte specie animali, ma appare di difficile definizione, in quanto consiste in una combinazione di moduli comportamentali derivanti da unità funzionali diverse (per es., caccia, lotta, comportamento sessuale), che vengono attivati indipendentemente da queste. In varie specie animali, i cospecifici riconoscono e distinguono il g. da altri comportamenti (per es., il g. della lotta rispetto alle interazioni aggressive vere e proprie). Si ritiene che esista una motivazione specifica per il g. basata sulla tendenza a esplorare, a conoscere cioè oggetti e situazioni ambientali, insieme a una forte motivazione motoria.

Il g. appare limitato ad alcuni Vertebrati. Non è stato infatti riscontrato negli Insetti e negli altri Invertebrati, negli Anfibi, nei Rettili e pressoché in tutti i Pesci; tra gli Uccelli il g. è presente in alcune specie, in particolare nei Corvidi; è invece diffuso in quasi tutti i Mammiferi, raggiungendo la massima plasticità nei Primati.

La varietà e l’importanza del g. appare correlata con la capacità di apprendimento e con lo sviluppo delle cure parentali. Il g., infatti, si può considerare una forma di apprendimento: giocando l’animale acquisisce la conoscenza del proprio corpo e delle proprie capacità, inventa nuove coordinazioni motorie, pratica e perfeziona schemi comportamentali che entreranno nel repertorio dell’adulto, interagisce con l’ambiente e con i conspecifici. Per giocare occorre una notevole disponibilità di tempo e di energia; l’animale non deve avere necessità immediate da soddisfare e deve essere al sicuro dai predatori: ciò si verifica soprattutto in specie nelle quali le cure parentali sono protratte nel tempo (Carnivori, Primati ecc.). La privazione del g. può alterare anche gravemente lo sviluppo del comportamento sociale e di quello sessuale dell’adulto.