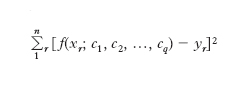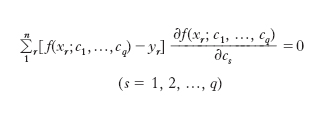minimo

Agraria

Legge del minimo

Legge che afferma che la quantità della produzione è regolata dall’elemento nutritivo contenuto nel terreno in proporzione minima rispetto agli altri. Corrisponde alla legge dei fattori limitanti (➔limitante).

Matematica

M. relativo di una funzione f(x) di variabile reale, definita in un dato intervallo, è il valore della funzione in un punto x₀ se in un suo intorno la funzione assume sempre valori maggiori o uguali al valore assunto in x₀. Se la funzione non è illimitata inferiormente, il minore tra i m. relativi è il m. assoluto della funzione.

Il minimo comune multiplo di due o più numeri interi è il più piccolo tra i numeri divisibili per tutti i numeri dati. Si trova scomponendo i numeri in fattori primi, e risulta formato come prodotto di tutti i fattori primi, comuni e non comuni, presi ciascuno col massimo esponente. Siano dati, per es., i numeri 36 e 60; si scompongono i due numeri in fattori primi; essendo 36=2²∙3², 60=2²∙3∙5, il m. comune multiplo dei due numeri sarà 180=2²∙3²∙5 e si scriverà: m. comune multiplo (36,60)=180. Se di due numeri è noto il massimo comun divisore, allora il m. comune multiplo si può ottenere rapidamente dividendo il prodotto dei numeri per il loro massimo comun divisore.

Il minimo comune multiplo di due o più polinomi, considerati in una o più variabili, con coefficienti reali, o complessi, o appartenenti a un corpo qualsiasi, si definisce come un polinomio di grado minimo, che sia multiplo comune dei polinomi dati; esso è determinato a meno di una costante moltiplicativa non nulla. Se di due polinomi è noto il massimo comun divisore, il m. comune multiplo si ottiene dividendo il prodotto dei polinomi per il loro massimo comun divisore.

Il metodo dei minimo quadrati serve a trovare il valore più probabile di una grandezza a partire da una serie di sue misure sperimentali. Sia x* il vero valore di una grandezza da misurare X; siano x₁, x₂, ..., x_n, i valori della grandezza ricavati da una serie di misure, affette da errori accidentali, e quindi diverse tra di loro e da x*. A partire da x₁, x₂, ..., x_n, si vuol determinare un valore x₀ il quale meglio approssimi (statisticamente) l’incognito x*. Secondo la teoria di Legendre-Gauss x₀ è il valore più probabile di X ed è quello che rende minima la somma dei quadrati degli errori accidentali:

ε₁ = x₀ − x₁; ε ₂ = x₀ − x₂; ...; ε _n = x₀ − x_n

(donde il nome del metodo). Come risultato, si ha che tale valore x₀ non è altro che la media aritmetica x̄ dei singoli valori x₁, x₂, ..., x_n.

Con lo stesso nome si indica il metodo per trovare, tra le funzioni di un certo tipo, quella che meglio approssima certi dati numerici. Più precisamente, siano assegnati n valori x₁, x₂, ..., x_n di una variabile x e altrettanti valori y₁, y₂, ..., y_n di una variabile y; sia inoltre data una certa funzione

f (x; c₁, c₂, ..., c_q),

reale di variabile reale, della variabile indipendente x, nella quale intervengono inoltre i parametri c₁, c₂, ..., c_q: si chiede di determinare c₁, c₂, ..., c_q, in modo che la funzione f assuma, in corrispondenza ai valori x₁, x₂, ..., x_n, rispettivamente i valori y₁, y₂, ..., y_n, oppure valori ‘quanto più possibile vicini’ a essi. Quest’ultima frase si può precisare in vari modi; il metodo dei m. quadrati precisa appunto che essa va così intesa: le c₁, c₂, ..., c_q, devono scegliersi in modo che sia minima la somma dei quadrati degli scarti tra i valori assunti dalla f per x=x₁, x₂, ..., x_n, e i valori assegnati y₁, y₂, ..., y_n, cioè l’espressione

intesa come funzione delle variabili indipendenti c₁, c₂, ..., c_q (➔ massimi e minimi). Quando si facciano opportune ipotesi sul campo di definizione della f e sulla sua regolarità, la soluzione del problema è da ricercarsi tra i gruppi di valori delle c₁, c₂, ..., c_q, che risolvono il sistema

Il metodo è spesso usato in pratica per ottenere un’interpolazione approssimata o una perequazione.

Medicina

In fisiologia, la legge del minimo limita il principio delle equivalenze degli alimenti, nel senso che una quota minima di certi alimenti (protidi, glicidi, lipidi) deve sempre entrare nelle diete.