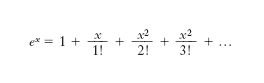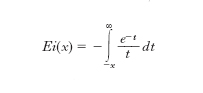esponente

Nella matematica elementare, e. di una potenza è il numero di fattori uguali tra loro, il cui prodotto esprime il valore della potenza. È scritto accanto alla base della potenza in alto a destra: 5³; (0,12)⁸, dove 3 e 8 sono gli e., 5 e 0,12 le basi. Quando si estende il concetto di potenza, l’e. può diventare un intero negativo o nullo, una frazione, e infine un numero, reale o complesso, una funzione ecc. (➔ potenza).

È detta equazione esponenziale un’equazione nella quale l’incognita appare a e. (per es., 2^3x+3^x=73, che ammette come soluzione x=2).

Funzione esponenziale è una funzione nella quale la variabile indipendente x compare come e., cioè ogni funzione di tipo y=a^x. Se si suppone a reale e maggiore di 1, e x reale, la funzione esponenziale risulta univocamente definita per ogni valore reale, e sempre crescente. In particolare, si dà il nome di funzione esponenziale (o solo esponenziale) alla funzione y = e^x, dove e = 2,7182... è la costante di Nepero (➔ Napier). Essa gode della fondamentale proprietà: è derivabile per ogni x, con derivata ancora uguale a e^x; di conseguenza la funzione risulta derivabile un numero infinito di volte e, sviluppandola in serie di Maclaurin, si ha la serie ( serie esponenziale):

che converge non solo per ogni x reale ma anche per ogni x complesso; si può perciò definire per mezzo di detta serie la funzione esponenziale nel campo complesso. In questa estensione restano valide le proprietà fondamentali di cui essa gode nel campo reale (y′=y″=...=y⁽ⁿ⁾=e^x; e^x1‧e^x2=e^x1+x2). Nel campo complesso, la funzione esponenziale è intimamente legata alle funzioni circolari dalla relazione di Eulero: e^ix = cos x+i sen x, che si stabilisce confrontando gli sviluppi in serie di Maclaurin delle tre funzioni. La curva rappresentativa della funzione y = a^x è detta curva esponenziale; se 0 〈 a 〈 1 essa ha come asintoto la semiretta positiva dell’asse delle x, e al contrario la semiretta negativa se a > 1 (nel caso a = 1 la funzione si riduce, naturalmente, alla funzione costante y = 1). Inoltre, le due curve y = a^x ed y = (1/a)^x = a^−x sono simmetriche l’una dell’altra rispetto all’asse delle ordinate.

Esponenziale integrale Funzione collegata all’integrale di e^−t/t e indicata con Ei, definita come

dove l’integrale è da intendersi come valore principale secondo Cauchy.