infinito

Lo spazio dalle dimensioni illimitate, o il tempo senza confini.

Filosofia

Il pensiero greco si è occupato fin dalle sue origini del concetto di infinito. Delle soluzioni proposte dai pensatori della scuola ionica per il problema delle origini e del principio ultimo delle cose, due fanno riferimento alla nozione di i.: Anassimandro riconduce tutto all’ἄπειρον, ovvero a una realtà illimitata, e Anassimene individua l’ἀρχή nell’aria concepita come infinita. Ma già nei pensatori successivi va affermandosi una diversa concezione dell’i., visto non già come realtà illimitata, ma piuttosto come concetto che rinvia a qualcosa di non finito e quindi imperfetto. Sia Platone sia Aristotele fecero propria la tendenza, già emersa con Parmenide, a identificare la realtà finita con la perfezione, l’ordine e l’armonia, e l’i. con la mancanza di misura e di determinazione. Aristotele considera l’i. come una nozione di cui si fa solo un uso negativo per suggerire che una certa realtà non è compiuta e non può quindi essere abbracciata nella sua totalità.

Sembra che Clemente Alessandrino sia stato il primo a predicare l’i. di Dio, sia pure in forma negativa, a indicare che egli è «privo di forma» e «senza nome»; più nettamente Basilio pone l’i. tra gli attributi di Dio, e Nicola di Metone afferma che l’i. è proprio solo di Dio. La teologia medievale approfondì il concetto di i. in rapporto all’essere di Dio. Una particolare accentuazione tale concetto assunse nella teologia mistica come carattere peculiare di Dio che lo pone al di là di tutte le predicazioni categoriali e quindi non attingibile per via positiva.

La filosofia moderna assiste a una mondanizzazione del concetto di i. sia facendone, come nel caso del naturalismo rinascimentale, un attributo della realtà che circonda l’uomo, sia permettendo all’uomo di attingervi facendosi partecipe dell’i. stesso. Questa è la via aperta da G. Bruno e poi ripresa, attraverso la mediazione di B. Spinoza, dall’idealismo tedesco. J.G. Fichte, F. Schelling e G.W.F. Hegel non contrappongono più il finito, l’individuo empirico, all’i., ma li collegano in un rapporto di partecipazione. Accanto a questa discussione della nozione metafisico-ontologica di i., la filosofia moderna e contemporanea ha approfondito l’analisi dell’i. come nozione quantitativa. Ancora nel 17° sec. Cartesio riprendeva la concezione aristotelica dell’i. quantitativo come indeterminato e dunque come concetto negativo. Ma proprio la filosofia moderna, specialmente con I. Newton e G. Leibniz, ha saputo fare del concetto di i. l’oggetto di analisi e calcoli positivi, suggerendo quel ribaltamento, divenuto operante nella matematica del 19° sec. con G. Cantor e J.W.R. Dedekind, per cui il concetto di i., da nozione paradossale, diviene una nozione del tutto padroneggiabile, sulla quale si può costruire un nuovo ampio settore di analisi per la matematica.

Fisica

La locuzione all’i. è usata per indicare la posizione di oggetti, di punti dello spazio e simili la cui distanza da particolari enti di riferimento sia molto grande rispetto ad altre distanze o lunghezze significative; per es., si dicono all’i. in ottica oggetti la cui distanza da un sistema ottico sia molto maggiore della distanza focale del sistema e in elettrostatica quelli la cui distanza dal sistema di interesse sia tale da non indurre perturbazioni nel valore del potenziale.

Linguistica

Verbo i. (o modi infiniti o indefiniti) è il complesso delle forme del verbo non finito (infinito, gerundio, participio e, in latino, gerundivo e supino), con funzione intermedia e oscillante tra nominale e verbale, la cui caratteristica è l’indeterminazione della persona, in contrasto con le forme del verbo finito, assieme alle quali partecipano però alla diatesi, nel caso del participio anche al numero e nel caso dell’infinito anche al tempo.

L’infinito in senso stretto è quella forma del verbo determinata nel tempo (leggere, aver letto) e nella diatesi (leggere, esser letto), ma indeterminata nella persona e nel numero, e capace di esprimere il processo verbale astratto; può essere sostantivato e quindi determinato come complemento (il leggere, con il leggere, al leggere ecc.; gr. τὸ λύειν, τοῦ λύειν ecc.; il latino supplisce con il gerundio). In italiano alcuni i. sono divenuti sostantivi (dovere, parere ecc.). Nelle lingue classiche, l’i. in un contesto narrativo può subentrare al posto dei tempi del passato (i. descrittivo o storico). In latino, meno frequentemente in greco, dopo i verbi che esprimono un’affermazione o dichiarazione, se il complemento non è un oggetto ma un’azione svolta da una persona, si ha l’accusativo con l’i. (proposizione oggettiva); questo costrutto può essere assunto anche come soggetto (proposizione soggettiva). Tutte le lingue indoeuropee possiedono la categoria dell’infinito.

Matematica

Il termine i. può assumere vari significati in questo ambito, anche notevolmente diversi tra loro.

L’infinito nella teoria degli insiemi e in aritmetica

Se si prende come punto di partenza il concetto di insieme finito, si potrà dire che un insieme è infinito quando esso non è «equivalente» a un insieme finito (cioè non si può porre in corrispondenza biunivoca, elemento per elemento, con un insieme finito). Ma si può anche dare una definizione diretta degli insiemi i. (R. Dedekind), come di quegli insiemi che possono essere posti in corrispondenza biunivoca con una loro parte propria (per es., facendo corrispondere a ogni numero intero n il suo doppio 2n, si pone una corrispondenza biunivoca tra l’insieme dei numeri interi e l’insieme dei numeri pari che è del primo un sottoinsieme o parte propria). Viceversa, questo non è possibile per un insieme finito.

G. Cantor, tra il 1879 e il 1884, estese il concetto di numero cardinale e di numero ordinale dal caso di insiemi finiti a quello di insiemi infiniti, introducendo numeri i. (o meglio transfiniti; ➔ transfinito), cardinali e ordinali. Il concetto fondamentale di Cantor è il seguente: attribuire lo stesso numero cardinale infinito (potenza o infinità dell’insieme) a tutti gli insiemi che possono essere posti in corrispondenza biunivoca, elemento per elemento, tra loro a due a due (per es.: l’insieme dei numeri naturali, dei numeri pari, dei numeri razionali).

L’i. in analisi

Si dice che una funzione y=f(x), della variabile reale x, tende all’i. (positivo) per x tendente a un dato valore x₀, quando, fissato un numero H positivo comunque grande, esiste un opportuno numero ε positivo tale che per tutti i valori della x, per i quali si abbia | x−x₀ | < ε, il valore di y=f(x) sia più grande di H (➔ limite). Analogamente si procede quando f(x) tende all’i. negativo ovvero quando ci si riferisca ad altri tipi di funzione. In questo senso per l’i. è di uso corrente il simbolo ∞ (che in un primo tempo venne adoperato per indicare l’uguaglianza, ed è una deformazione delle prime lettere della parola aequalis); si scrive pertanto:

lim_x→x0 f(x) = + ∞, ovvero lim_x→x0 f(x) = − ∞.

fig. 1A

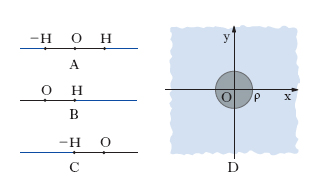
Nel caso di una funzione che tende all’i. si dà una definizione dell’i. come limite; o, se si vuole, si definisce l’i. per mezzo dei suoi intorni. Sarà da chiamarsi intorno completo dell’i., nel caso di una variabile (fig. 1A), l’insieme dei numeri, positivi e negativi, il valore assoluto dei quali supera un dato numero positivo H «grande a piacere»; un intorno di +∞ sarà invece l’insieme dei numeri positivi superiori a H (fig. 1B); un intorno di −∞ l’insieme dei numeri negativi minori di −H (fig. 1C). Analogamente (fig. 1 D), nel piano della variabile complessa z=x+jy (➔ numero) o nello spazio a r dimensioni nel quale sono rappresentati mediante punti i gruppi di valori di r variabili indipendenti x₁, x₂, ..., x_r, un intorno dell’i. è l’insieme dei valori di z il cui modulo supera un valore positivo dato ρ (cioè l’insieme dei punti esterni al cerchio di centro origine, O, e raggio ρ), o, rispettivamente, l’insieme dei punti aventi dall’origine una distanza maggiore di ρ.

Si dice che una funzione è un i. quando, in un opportuno passaggio al limite, il suo valore assoluto tende a +∞. In particolare, una funzione reale f(x) è un i. per x→x₀ (cioè

per x tendente a x₀) se lim_x→x0 ∣ f(x) ∣ = + ∞.

Due funzioni f(x), g(x) che siano due i. simultanei per x→x₀, sono dette i. dello stesso ordine se il loro rapporto, per x→x₀, tende a un limite finito e diverso dallo zero, o si mantiene, da un certo punto in poi, compreso tra due costanti non nulle e con lo stesso segno. Restando ferma la prima ipotesi, si dice che g(x) è un i. di ordine superiore rispetto a f(x) se

f(x)

lim_x→x0 −−−− = 0

g(x)

[in forma intuitiva: g(x) tende a ∞ «più rapidamente» di f(x)], si dice invece che g(x) è un i. di ordine inferiore se, al contrario,

lim_x→x0 f(x)/g(x) = ∞

[in forma intuitiva: g(x) tende a ∞ «più lentamente» di f(x)]; se non esiste il limite di f(x)/g(x) per x→x₀, i due i. non sono paragonabili. Infine, assunta f(x) come i. campione, si dirà che g(x) è un i. di ordine n rispetto a f(x), se g(x) e [f(x)]ⁿ sono i. dello stesso ordine; n si chiama l’ordine di infinito.

L’introduzione sistematica dell’i. come limite nell’analisi matematica è dovuta ad A. Cauchy (Analyse algébrique, 1821), il quale definì nel tempo stesso come limite gli infinitesimi.

L’infinito in geometria

fig. 2A

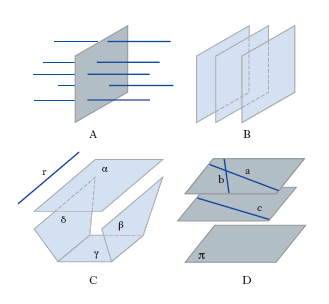
In geometria si considerano elementi all’i. (o impropri). In geometria proiettiva si chiama punto all’i. di una retta la sua direzione (l’astratto della classe delle rette parallele alla data), retta all’i. di un piano la sua giacitura (l’astratto della classe dei piani paralleli al dato), piano all’i. dello spazio l’insieme dei punti e delle rette all’infinito. Le nozioni di punto all’i. e di retta all’i. permettono di formulare in modo elegante le situazioni di parallelismo tra rette e tra piani: così, rette con il medesimo punto all’i. sono rette parallele (fig. 2A) e piani con la stessa retta all’i. sono piani paralleli (fig. 2B), mentre piani che hanno in comune un punto all’i. sono paralleli a una stessa retta, ma non paralleli tra loro (fig. 2C: i piani α, β, γ, δ hanno in comune il punto all’i. della retta r) e rette che hanno i rispettivi punti all’i. su di una stessa retta sono rette parallele a uno stesso piano ma non, in generale, parallele tra loro (in fig. 2D le rette a, b, c hanno i punti all’i. allineati sulla retta all’i. del piano π). Mentre nel piano proiettivo i punti all’i. sono ∞¹ (uno per ciascuna retta di un fissato fascio di centro proprio), nel piano della variabile complessa, o piano-sfera, vi è un solo punto all’i., che è quello che convenzionalmente si fa corrispondere al centro di proiezione quando il piano-sfera α si pensi ottenuto mediante proiezione stereografica di una sfera (cioè mediante proiezione fatta da un punto della sfera nel quale il piano tangente sia parallelo ad α). Si noti inoltre che un punto che si muova sulla retta proiettiva in un senso o nell’altro tende a un medesimo punto all’i., qualunque sia il senso di percorrenza della retta (ha senso parlare di +∞ e −∞ per la retta euclidea, che è aperta, non per la retta proiettiva).